基于一维灰度投影的拼接币左右编号匹配识别算法

王志杨， 刘金龙

(1.安徽电子信息职业技术学院 电子工程系，安徽 蚌埠 233030；2.江苏海洋大学 电子工程学院，江苏 连云港 222005)

引言

拼接币是一种人为拼接制造的假币。这类拼接币人眼很容易识别，自动存款机却无能为力。犯罪分子的手法就是将真、假百元人民币各一张先进行剪切，再用透明胶带将部分假币和部分真币粘起来制造出两张“半假钞”，然后将此“半假钞”的拼接币存入自动存款机，再从其他取款机取出真币，以这种方式完成“洗假钱”。此类案件最早是在广州发现的，并且迅速蔓延到全国各地。各省的自动存款机中都发现了大量这样的拼接币，致使有关商业银行停止了这些自动存款机的使用，给银行和广大人民群众带来了极大的损失[1-3]。

由于市场上流通的人民币不可能都是十成新的，为了使人们方便的使用存款机，几乎所有的自动存款机都降低了验钞的识别参数标准，一般只要与标准样本数据库的数据匹配达到70%到80%，就受理自动存款业务[4]。而且现在港版伪钞和台版伪钞也有荧光反应，如果用这类伪钞和真币进行拼接就使得自动存款机识别拼接币难上加难了。同时，由于每台自动存款机的造价昂贵，最少要几十万，如果全部更换的话会给银行造成很大的负担。本项目旨在根据最新2015版百元钞票的图像特征，运用图像处理技术处理拼接币的图像，通过边界提取和图像特征匹配等运算来识别2015版拼接币，并进行仿真验证，给出一套识别拼接币的算法方案和软硬件模型，改进自动存款机的验钞系统。

拼接币的图像特征主要有以下两点：(1)有胶带；(2)左右编号不一致。基于这两点特征作为识别拼接币的主要依据。

纸币图像的采集通过摄像头可以精确获取，并储存为JPEG图像格式。因为处理的编号区是纸币的细节特征，要求摄像头采用高分辨率设备。本文先以真币为目标，处理后得到256级灰度图，再推广到拼接币。人民币样本的扫描分辨率是1830*920像素，拍摄速率是30帧/s。

1 总体思路

在本项目中，采用图像处理技术提取拼接币图像中的编号区域和胶带区域，并利用一维灰度投影模板匹配法和门限法对拼接币进行检测与识别。具体过程如下：

(1)采集图像并进行RGB三分量分割；

(2)对(1)的R分量图像应用边缘检测法从背景中获得钞票区，以减少处理的数据量；

(3)为使随后的处理更加简单，对(2)图像进行二值化、灰度均衡等预处理；

(4)应用精准定位法分割出左右编号区域；

(5)计算(4)区域的一维灰度投影曲线，并根据投影曲线分割每一个字母或数字；

(6)进行一维灰度投影模板匹配，求出每个字母或数字的相关系数，与门限值进行比较，判断左右编号是否互相匹配；

(7)对(1)的B分量图像进行预处理，突出胶带区；

(8)选择合适的灰度门限值对(7)的图像进行二值化，分离出胶带(剩下为背景区)，计算胶带区像素数，并与设定的像素数比较，如大于设定值则判定有透明胶带。

因篇幅限制，本文仅探讨左右编号匹配识别前的部分。

2 左右编号的识别

2.1 编号区定位分割

由于人民币的设计相当规范，虽然编号区不尽相同，但都在一个固定的区域，因此可以先对编号区进行初定位[5]。初定位是根据预测定位编号区，只是一个参考值，如图1所示。大区间定位则是在初定位的基础上增加区域的偏移量，使区域加大，以保证编号落在整个定位区域内[6]。定位偏移量的选择要综合考虑，过大将导致多余信息落入处理区，增加运算负担；过小将导致处理区号码不完整。左编号大区间为(60∶460横向,660∶750纵向)，右编号大区间为(1660∶1750横向,370∶770纵向)，如图3所示为大区间定位分割出来的左右编号区，图b)是将右编号顺时针旋转90度后的图像。

图1 真币扫描图Fig.1 Scanned image of real money

图2 拼接币识别流程图Fig.2 Flowchart of spliced money recognition

图3 大区间定位a) 分割的左编号；b) 分割的右编号Fig.3 Large interval locationa) Divided left number；b) Divided right number

2.2 编号区图像预处理

上图可以看出，从噪声图像中分割出的左编号背景图像简单清晰，只有一些简单的独立点和低灰度值的背景区域；而右编号的背景图像则相当复杂，且与字符紧密地连接，使提取字符特征变得复杂。因此需要进行适当的图像预处理，去除背景图像，突出字符特征并且尽量使字符图像不失真。

2.2.1 图象增强 图3中右编号的背景图像相对较复杂且与字符的灰度级数相差不大，这一点可以从左右编号的灰度直方图4 a)、b)相比较得出。因此，采用图像增强中的直方图均衡法对右编号进行灰度增强，将背景和字符区的灰度值进行延拓，突出字符区的灰度值[7-10]。结果如图4 c)、d)，很明显字符区相对于背景的灰度值明显变小了。

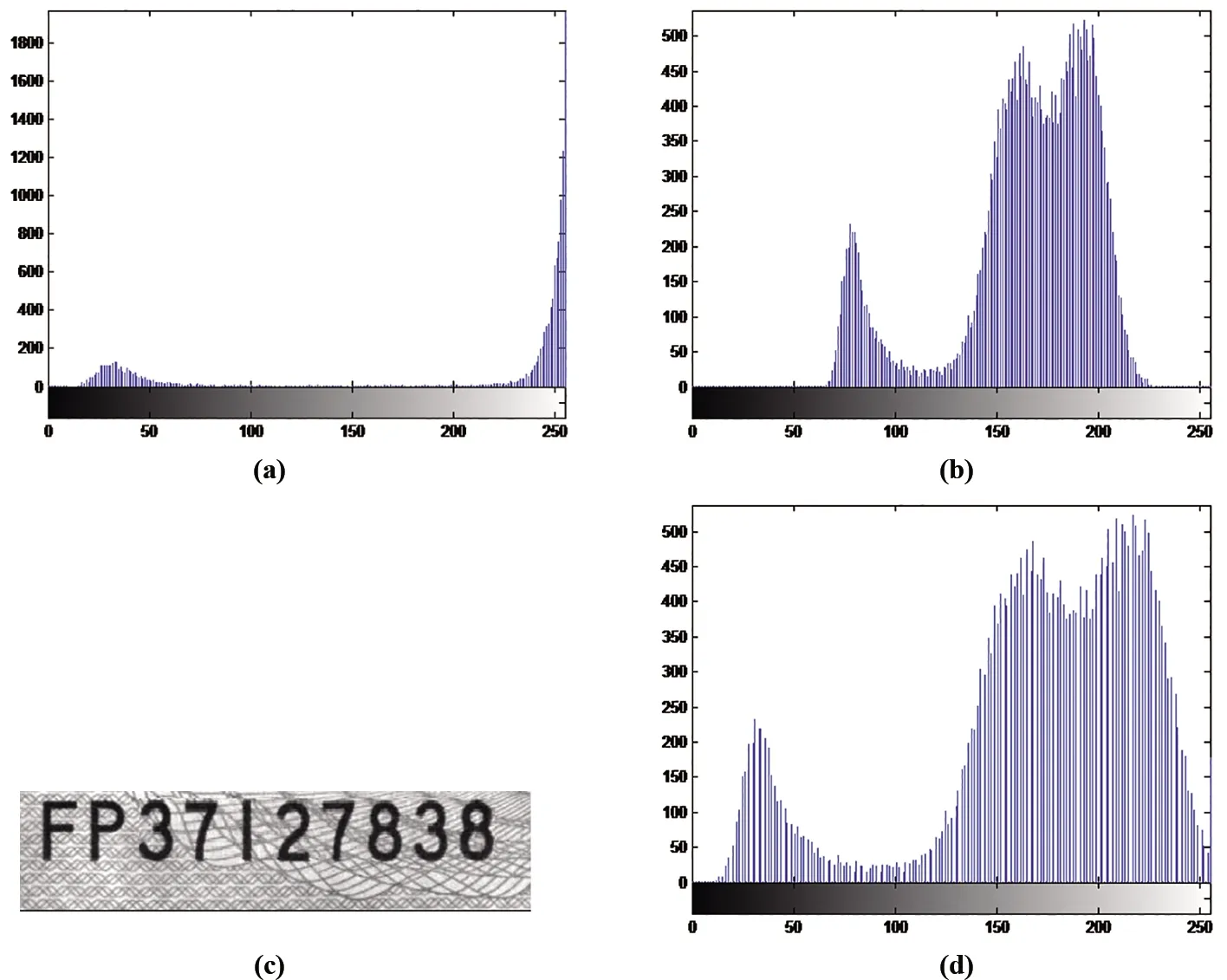
图4 右编号灰度均衡化a) 左编号灰度直方图；b) 右编号灰度直方图；c) 灰度均衡后的右编号；d) 灰度均衡后右编号直方图Fig.4 Gray equalization of right numbera) Gray histogram of left number；b) Gray histogram of right number；c) Right number after gray equalization；d) Gray histogram of right number after gray equalization

2.2.2 图像二值化 图像二值化是将多级灰度图像转换成只有两个灰度值的图像，是一种简化了的灰度图像。经过图像均衡化后的右编号存在两个明显的峰值和一个谷值，且字符区的灰度范围就在低灰度值范围内[11]。因此采用整体阈值法对左右编号二值化，门限值为128，灰度值大于128的为“1”，反之为“0”，如图5所示。

图5 图像二值化a) 左编号二值化；b) 右编号二值化Fig.5 Image binarizationa) Binarization of left number；b) Binarization of right number

2.2.3 反色 左右编号经过二值化后，背景区域值为“1”，字符区域值为“0”，这样给处理字符区域带来不便，且存储的数据量大。因此，根据反色的原理，将背景区域的值转换为“0”，字符区转换为“1”，方便对字符区的处理和分析[12]。反色结果如图6所示。

图6 反色a) 左编号反色；b) 右编号反色Fig.6 Reverse colora) Reverse color of left number；b) Reverse color of right number

2.2.4 平滑滤波 平滑滤波可以减小图像获取和传输过程中的噪声干扰[13]。本文采用平滑滤波中的中值滤波算法，模板选取3 x 3。如选择5x5 或7x7模板，效果改善并不明显。但是运算量会增加。所以3 x 3模板已经足够。

中值滤波的方法易于实现，且较好得保护了边界。图7是经过中值滤波后的图像，与图6中各个字符的边界进行比较，可以发现图7各个字符的边界变得连续，无间断点，充分达到了保护边界的目的。

图7 平滑滤波(中值)a) 对左编号中值滤波；b) 对右编号中值滤波Fig.7 Median filtera) Median filter of left number；b) Median filter of right number

2.3 二值形态学处理

从图7中可以看出，左右编号各个字符的边界存在着一些非边界的点，当图像的质量比较差，还会有大量的噪声孤立点。腐蚀和膨胀运算可以除去噪声孤立点，来达到光滑字符边界的目的，并保留原图像的基本信息[14]。

如图8 a)、b)所示，采用结构元素为se的矩阵，利用腐蚀运算将左右编号的每个字符区域缩小，字符竖划中较细的笔划在腐蚀的过程中被消除。利用这一点，可以使文字中的孤立点分离出来。然后采用相同的结构元素对字符进行膨胀运算，文字区域扩大且达到光滑文字边界的目的，如图8 c)、d)。

图8 对左右编号进行二值形态学处理a) 对左编号腐蚀；b) 对右编号腐蚀；c) 对a) 进行膨胀；d) 对b) 进行膨胀Fig.8 Binary morphology processing of left and right numbersa) Erosion of left number；b) Erosion of right number；c) Expansion of a)；d) Expansion of b)

(1)

2.4 精准定位

精准定位是在大区间定位的基础上，滤除干扰，完成左右编号区每个数字或字母的分割定位[15,16]。对图8中的c)、d)进行精准定位。具体过程如下：

(1)计算出左右编号的一维水平灰度投影和一维垂直灰度投影，如图9中的a)、b)、c)、d)所示；

(2)根据水平灰度投影曲线计算出灰度零点，并计算出垂直灰度投影曲线的两个零点；

(3)以边界点分别取垂直方向的两个零点，水平方向首尾两个零点截取左右编号中的字母或数字，完成精准定位运算。结果如图9中的e)、f)。

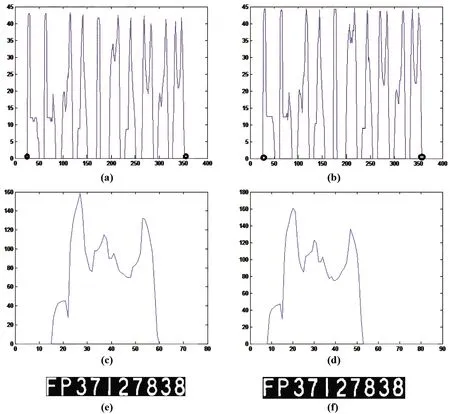
图9 精准定位分割后的左右编号a)左编号一维水平灰度投影曲线；b) 右编号一维水平灰度投影曲线；c) 左编号一维垂直灰度投影曲线；d) 右编号一维垂直灰度投影曲线；e) 精准定位分割后的左编号；f) 精准定位分割后的右编号Fig.9 Precise location divided left and right numbersa)One-dimensional horizontal gray scale projection curve of left number；b) One-dimensional horizontal gray scale projection curve of right number；c)One-dimensional vertical gray scale projection curve of left number；d) One-dimensional vertical gray scale projection curve of right number；e)Precise location divided left number；f)Precise location divided right number

2.5 字符分割

具体过程如下：将图9 a)、b) 中的零点按顺序两两分组，字符数作为分组数；再以图9 a)中的每一组零点和图9 c)零点为边界点截取得到左编号各字符，同理得到右编号各字符[17]。结果如图10。

图10 左右编号字符分割a)左编号字符分割；b) 右编号字符分割Fig.10 Character division of left and right numbersa)Character division of left number；b) Character division of right number

2.6 模板匹配识别拼接币

模板匹配算法有传统的空域二维模板匹配算法、频域卷积模板匹配算法和本文提出的一维灰度投影模板匹配算法。现在分别使用三种算法对左右编号进行模板匹配运算，并分析比较，找出快速又准确的算法。

2.6.1 空域二维模板匹配算法 以图10中分割出来的第八个字符8为例，左编号中的8为模板，右编号中的8为待匹配子图(目标图像)，如图11所示。根据传统空域二维模板匹配算法，将模板图像8(图11a))在待匹配图像(图11b))上平移，并计算二者的互相关函数值，得出互相关系数序列。选择最佳阈值，并将互相关系数序列中的最大值与阈值进行比较，如果大于最佳阈值就说明两个字符匹配，即两字符相等；如果小于最佳阈值，则说明两字符不相等，即左右编号不匹配。根据匹配结果，当左右编号的每一个字符都匹配时，说明存入自动存款机中的钞票是真币；只要左右编号中有一个字符不匹配，就判定存入自动存款机中的钞票是拼接币。

图11 空域二维模板匹配a) 模板；b) 待匹配图像Fig.11 Two-dimensional template matching in space domaina) Template；b) Image to be matched

图11中字符8空域二维模板匹配的互相关系数值为0.9089，而整个左右编号的互相关系数序列为0.9396、0.9037、0.8682、0.8982、0.9279、0.8893、0.9443、0.9089、0.8995、0.8884。本文一共扫描了100张图像，采集到100组互相关系数序列。根据实验结果，选择0.82为相关系数最佳阈值，当左右编号相关系数均大于0.82时，判定为真币；当左右编号中只要有一个字符小于0.82时，就判定纸币为拼接币。

实验结果表明，利用空域二维模板匹配算法识别拼接币左右编号是否一致完全可行，只要阈值选择合适，识别正确率可以达到95%以上。该算法是一种精确的匹配算法，且模板选择越小越好。但是，这种算法的计算量相当大[18]，不能快速实现，其计算量一般为：O(H-M+1)×(W-N+1)×M×N(M*N为模板像素，W*H为待匹配图像像素)。本文不采用这种方法。

2.6.2 一维灰度投影模板匹配算法 针对课题研究的图像特点，匹配对象是具有固定形状的字符，且字符间存在一定的空白间距，本文提出了一种新的算法，一维灰度投影模板匹配算法。一维灰度投影模板匹配算法是分别将模板和待匹配图像的二维图像灰度值投影迭加到一维数轴上，并在一维数轴上分别从横轴和纵轴两个方向进行匹配判断，运算量降低到：

O′(H-M+1)×(H×W+(H-N+1)×N)

图12 一维灰度投影匹配Fig.12 One-dimensional gray scale projection matching

基本原理：灰度投影曲线充分反映了其在水平和垂直方向的上的灰度分布特征。首先求出待匹配图像S第j层图像和模板图像T的两个方向的灰度投影，得到待匹配图像投影序列X[i]、Y[i]和模板图像投影序列X1[i]、Y1[i]。然后，将模板投影曲线滑动经过第j层投影曲线，计算滑动过程中每个位置的互相关函数R[i]，由此产生一组互相关系数序列。选取最佳门限值，并用序列的最大值与该值比较，如果R[i]大于门限值，说明该子图与模板图像匹配。最后，对待匹配图像S的[1，H-M+1]层依次进行如上运算，最终求出匹配子图的位置。

一维灰度投影匹配的相关函数为：

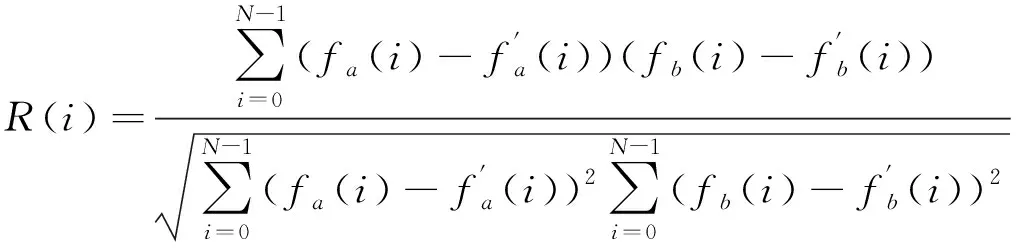
(2)

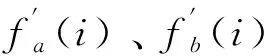
采用一维灰度投影模板匹配算法。同样以字符8为例，首先做出模板8和待匹配图像8各自的两个方向的投影曲线，如图13中a) 、b)所示；其次根据式(2)分别计算两者的水平和垂直灰度投影曲线序列的互相关函数序列；最后将序列最大值与最佳阈值比较。如果大于最佳阈值就说明两个字符匹配，即两字符相等；如果小于最佳阈值，则说明两字符不相等，即左右编号不匹配。

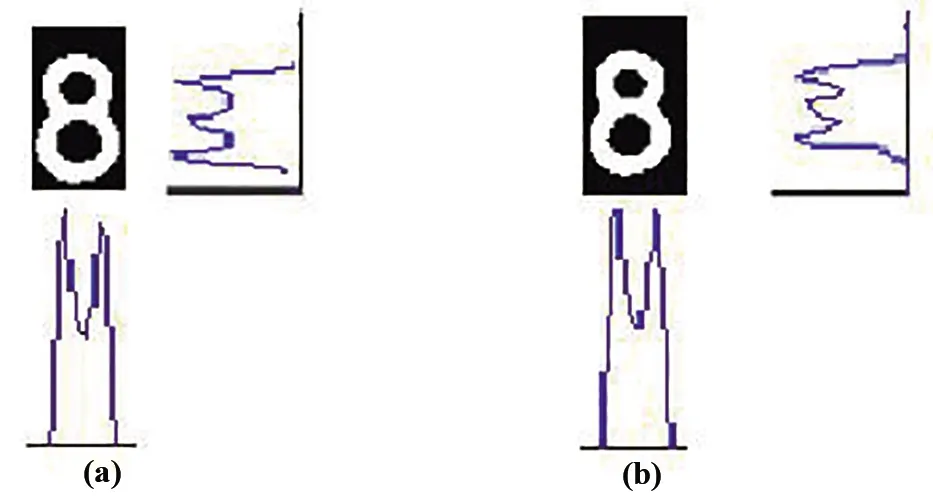
图13 一维灰度投影模板匹配过程a) 模板的水平和垂直灰度投影；b) 待匹配图像水平和垂直灰度投影Fig.13 Process of one-dimensional gray scale projection template matchinga) Horizontal and vertical gray scale projection of template；b) Horizontal and vertical gray scale projection of image to be matched

图13中字符8一维模板匹配的水平灰度投影互相关系数值为0.9681，垂直灰度投影互相关系数值为0.9707，而整个左右编号的一维水平灰度投影互相关系数序列为0.9757、0.9792、0.9640、0.9733、0.9820、0.9771、0.9908、0.9681、0.9754、0.9641，一维垂直灰度投影互相关系数序列为0.9578、0.9284、0.9903、0.9680、0.9559、0.9876、0.9485、0.9707、0.9941、0.9792。同样，本文根据采集到的100组互相关系数序列，选择0.85为水平一维灰度投影模板匹配的互相关系数最佳阈值，选择0.90为垂直一维灰度投影模板匹配的互相关系数最佳阈值。

实验结果表明，利用一维灰度投影模板匹配算法识别拼接币左右编号是否一致是一种快速、高效的方法，并且识别正确率达到100%。在这里应该注意，只有字符的水平和垂直灰度投影都满足大于阈值的条件才可以判定左右编号匹配，只要一个方向不满足，均视为拼接币。

2.6.3 频域卷积模板匹配算法 频域的模板匹配原理是：将模板图像T与待匹配图像S进行相关运算，也就是将模板T和待匹配图像S进行傅立叶变换，根据快速傅立叶变换和卷积的关系，计算矩阵的卷积，并提取峰值[19]。如果峰值大于门限值，则这一点就是匹配图像的位置。傅立叶变换的卷积性质为：

[f(x,y)*g(x,y)]↔F(u,v)G(u,v)

(3)

同样以图10中分割出来的第八个字符8为例，左编号中的8为模板，右编号中的8为待匹配子图。根据式(3)，可以通过频域乘积得出字符8的另一类互相关系数为63.8185，而整个左右编号的频域乘积再傅立叶反变换得到的互相关系数序列为54.5353、53.2515、50.5458、40.8258、26.8501、52.1880、41.0037、63.8185、50.3796、67.5072。

同样，本文根据采集到的100组互相关系数序列，从结果和数据可以得出频域的模板匹配原理与空域二维匹配方法类似，只是在卷积的过程中运用了傅立叶变换的卷积性质，使得计算快速有效；但是，可以从上一组数据看出，当字符的像素较少时，互相关系数值很小，例如“1”这个字符的系数值就为26.8501，此外还有“7”。因此，无法选择合适的阈值对相关系数序列进行判定。因此本文不采用这种算法。

3 结论

本文提出了一套自动存款机识别拼接币的算法，重点介绍了采用图像处理技术对于采集纸币图像的预处理，并对比介绍了传统的空域二维模板匹配算法、频域卷积模板匹配算法和本文提出的一维灰度投影模板匹配算法识别左右编号的技术。通过仿真和实验证明，该算法识别正确率达到了100%。识别程序在内存4GB、CPU为2．4GHz(两核)的PC上，运行时间为3．325s。将程序优化并进行语言转换后下载到DSP硬件系统中，其运行时间为0．52s，满足实时性要求，方案切实可行，为自动存款机识别拼接币奠定了基础。