斜腿刚构曲线连续梁人行桥人致振动风险研究
2021-10-20周涛陈谨林牛华伟孟杰
周涛,陈谨林,牛华伟,孟杰
(1. 中南大学 土木工程学院,湖南 长沙 410075;2. 林同棪国际工程咨询(中国)有限公司,重庆 401121;3. 湖南大学 振动与冲击技术研究中心,湖南 长沙 410082)
统计分析表明,人正常步行的频率约为2 Hz,在1.7~2.3 Hz之间并呈正态分布[1]。随着材料科学的发展和人们对桥梁景观要求的提高,钢结构广泛用作人行桥的主梁或墩柱,人行桥跨度越来越大、结构造型也愈加个性、美观。其结果便是人行桥的刚度小、频率低,如果桥梁的频率低至行人步频范围内,将会导致人、桥共振,影响行人舒适性,而采用钢结构的人行桥由于阻尼比小,共振现象愈发严峻。因此,在大跨度人行桥的设计阶段需要特别关注人致振动问题。实际上,自从2000 年伦敦千禧桥因发生大幅人致振动而被迫关闭的事件发生之后[2],各国学者对人致振动问题开展了深入而广泛的研究,对新建人行桥梁进行人致振动响应计算。ELSA等[3]以位于葡萄牙Coim‐bra 市Mondego Green 公园的一座主跨110 m,宽度4 m的双飞燕扁拱桥为工程背景,用模态法计算了该桥的人致振动响应,结果表明最大加速度响应超过了英国规范BS5400[4的要求。罗晓群等[5]以单斜面索拱支承曲梁人行桥为研究对象,模拟计算了随机人群荷载对结构的响应,发现桥梁跨中竖向加速度峰值的0.95 分位数为 1.506 0 m/s2,大于中国规范CJJ/69[6]规定的竖向加速度限值。当行人引起的桥梁加速度响应超过允许值时,可以通过提高结构自振频率和增加结构阻尼2个方法来解决问题。提高结构自振频率意味着要增加结构刚度和减小质量,工程实际表明,这两者往往是相悖的,因此,这个方法不太可行。目前,国内外常用增加结构阻尼的方法来降低人行桥的人致振动响应,而设置调谐质量阻尼器(TMD)是普遍用于增加人行桥阻尼的措施。英国伦敦千禧桥上安装了38 个黏滞阻尼器和60 个TMD 之后,水平模态阻尼比提高到15%~20%,竖向模态阻尼比提高到5%~10%[2]。葡萄牙Combia 桥安装了1 个水平TMD 和6个竖向TMD,水平模态阻尼比从0.5%增加至4.0%;竖向阻尼比从0.3%~2.2%增加至3%~6.0%。我国的绵阳市1 号桥安装了质量共计14 t 的水平TMD 和46.1 t 的竖向TMD,在400 人同时在桥的情况下,桥梁水平加速度峰值由0.1 m/s2降低到0.08 m/s2,竖向阻尼比提高到5.5%[7]。由此可见,TMD可以有效控制人致振动响应。
1 工程概况
本文研究对象为斜腿刚构曲线连续梁人行桥,跨径布置为35+75+20=130 (m)。主梁主体结构为单箱单室钢箱梁结构,梁端靠近承台处设置混凝土梁段并设置钢−砼结合段形成主梁与桥台固结的整体式桥台,梁高1 m,宽5 m。桩基、承台、地系梁、桥台及斜腿桥墩下部为混凝土结构,主墩靠近承台处为钢筋混凝土墩,墩梁结合段为钢结构,钢结构桥墩与混凝土桥墩连接处设置钢−砼结合段。主梁平面位于曲线半径R=22.5 m 的右偏圆曲线、直线上。桥面设1%单向横坡,横坡均朝曲线外侧设置。桥梁中跨设置竖条廊架和休息座椅。大桥效果图、立面图、平面图及断面图见图1~图4,立面图中填充部位是混凝土结构,未填充部位为钢结构。

图2 桥梁立面图Fig.2 Elevation of the bridge
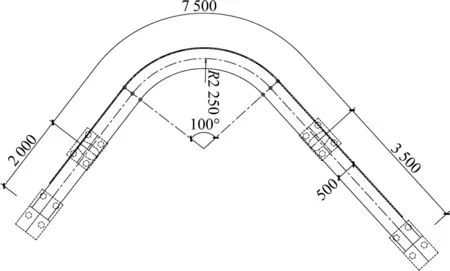
图3 桥梁平面图Fig.3 Plan of the bridge
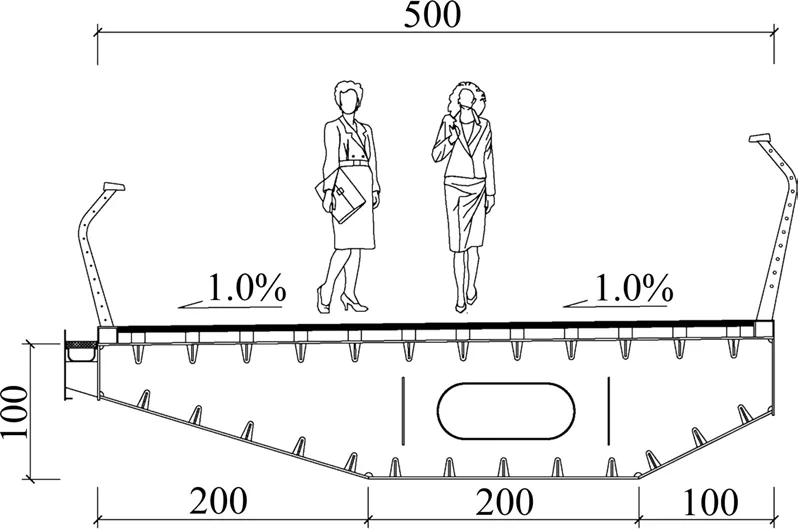
图4 桥梁横断面布置图Fig.4 Cross-section of the bridge deck
作为跨度大、主梁高度小的钢结构人行桥,本桥具有刚度小且结构阻尼比低的特点,行人荷载引发大幅振动的风险较大,有必要开展人致振动响应分析及振动风险控制研究。
2 行人荷载模型及舒适度评价
2.1 单人荷载模型
人在行走的过程中,双脚交替运动,一般情况下脚跟先着地,然后脚尖离地迈步,每迈一步,行人的重心会上下起伏一次,从而产生竖向的动荷载。与此同时,人在往前走时,左右脚总是呈“Z”字形交替运动,引起人的重心左右摆动,从而产生横向动荷载。另外,行人前进的过程中需要克服地面摩擦力,因此,行人荷载也会产生纵向力。典型的步行力时程曲线如图5所示[8]。
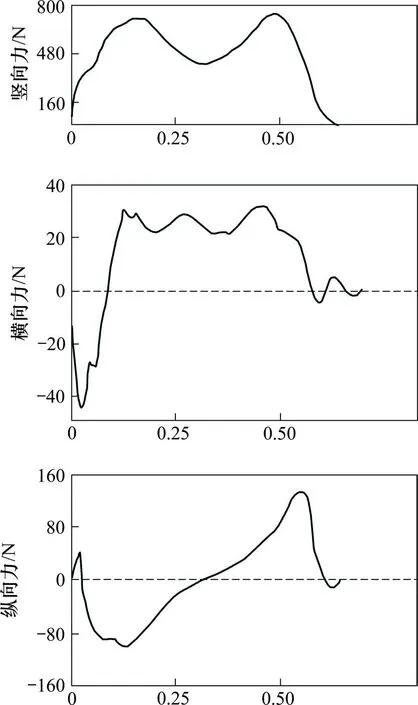
图5 单步力竖向、横向和纵向分量Fig.5 Single step walking time histories in vertical,lateral and longitudinal directions
虽然人与人之间的体重、身高等特征都不尽相同,行人对桥梁等结构的荷载却具有明显的周期性和窄带随机的特点,单个人的脚步力时程可以用傅立叶级数来表示[9]。
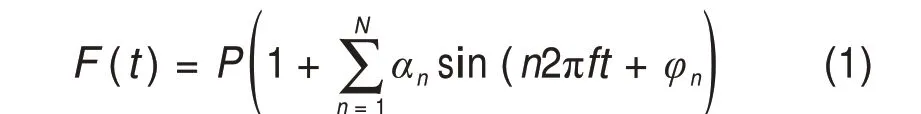
式中:P为单人体重;f为行人步频;αn为第n阶简谐动载系数;φn为第n阶动载初相位。
2.2 人群荷载模型
由于人对桥梁结构作用的随机性以及人桥相互影响,相比于单人荷载模型,人群荷载更难用数学模型表述。目前,关于人群荷载的模拟,通常基于统计分析,并在单人荷载叠加作用的基础上考虑折减。基于各国学者所取得的研究成果,多个国家颁布了人行桥人致振动的计算法则。对于人群荷载模型,本文参考德国人行桥设计指南EN03 规范[10],该规范考虑行人脚步力的前2 阶谐波荷载,其荷载模型如下:
p(t) =p× cos(2πfst)×n′ ×ψ(2)
其中:P是步频为fs时单个行人产生的荷载幅值,竖向取280 N,横向取35 N,纵向取140 N;fs为步频,假设它等于所考虑的人行桥基频;S为加载面积;n'为等效行人密度;ψ为考虑到步频接近基频变化范围临界值的概率而引入的折减系数,其取值方法见图6。
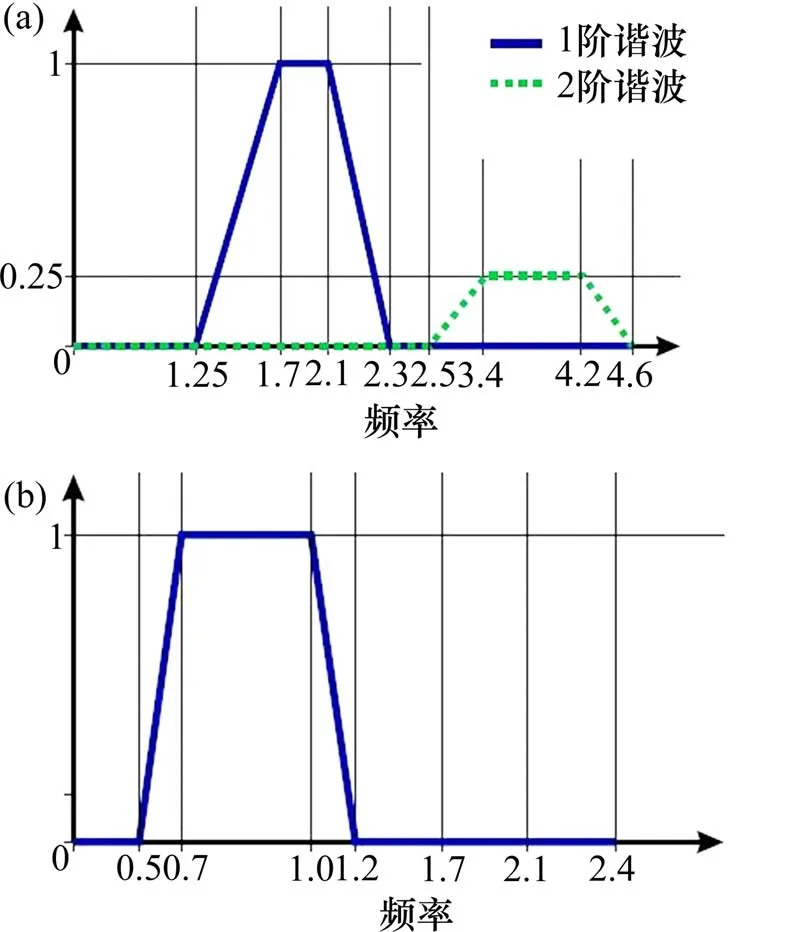
图6 折减系数Fig.6 Reduction factor
当人群密度d<1.0 P/m2时:

当人群密度d≥1.0 P/m2时:

式(3)中ξ为结构的阻尼比,n是加载面积为S时的行人数(n=S×d)。
谐波荷载p(t)被施加到结构的某一特定振型上,如图7所示。
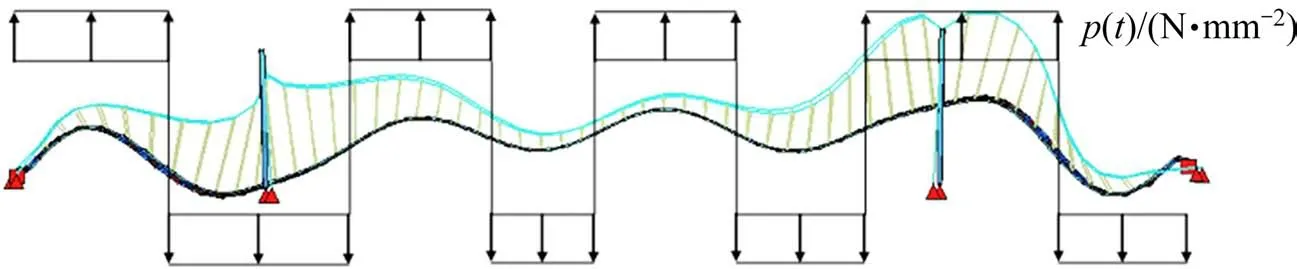
图7 加载模式Fig.7 Loading mode
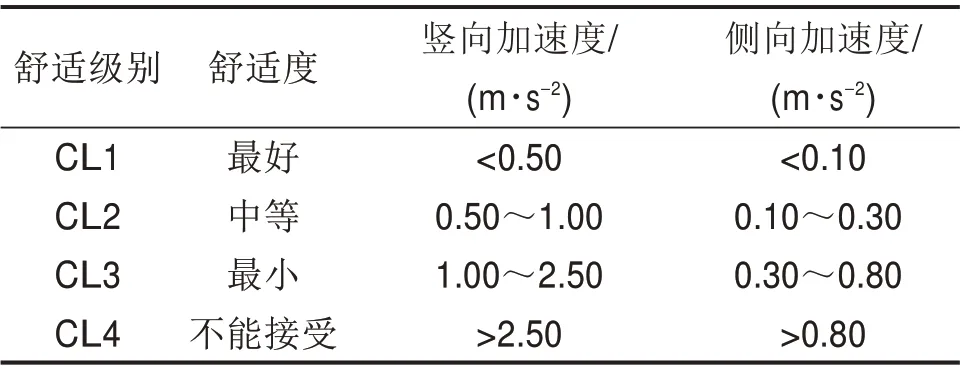
表1 德国EN03规范定义的行人舒适度评价标准Table 1 Pedestrian comfort evaluation standard defined by German EN03 standard
2.3 舒适度评价
当人行桥发生过大的振动时,会导致行人不舒适。由于人体对加速度比较敏感,目前,人行桥的舒适度常用加速度值来衡量。在舒适度限值的取值方面,德国EN03 规范[10]采用分级定值法,根据加速度的大小分为4个等级。
3 有限元计算分析
3.1 有限元模型说明
采用有限元分析软件Midas Civil 2020 建立了有限元模型,所有构件均采用梁单元模拟,其中,主梁材质为Q420 钢材,桩基采用C35 水下海工混凝土,承台和地系梁材质为C45海工混凝土,钢混结合部及桥台材质为C50混凝土。该桥址处于入海口,场地内地层自上而下依次为:人工填土层、沉积层、洪积层、残积层,下伏基岩为花岗岩,采用桩端入岩的灌注桩,且最长的桩长达33.5 m,桩基的边界条件对动力特性有很大的影响,依据地址资料和桩土相互作用分析,桩基、地系梁与周边土之间设置为弹性支承,桩基底部设置为固结。有限元模型如图8所示。

图8 桥梁有限元模型Fig.8 Finite element model of the footbridge
3.2 模态特征
基于多重Ritz向量法进行特征值分析,得到结构前10阶的模态频率及振型特征见表2。
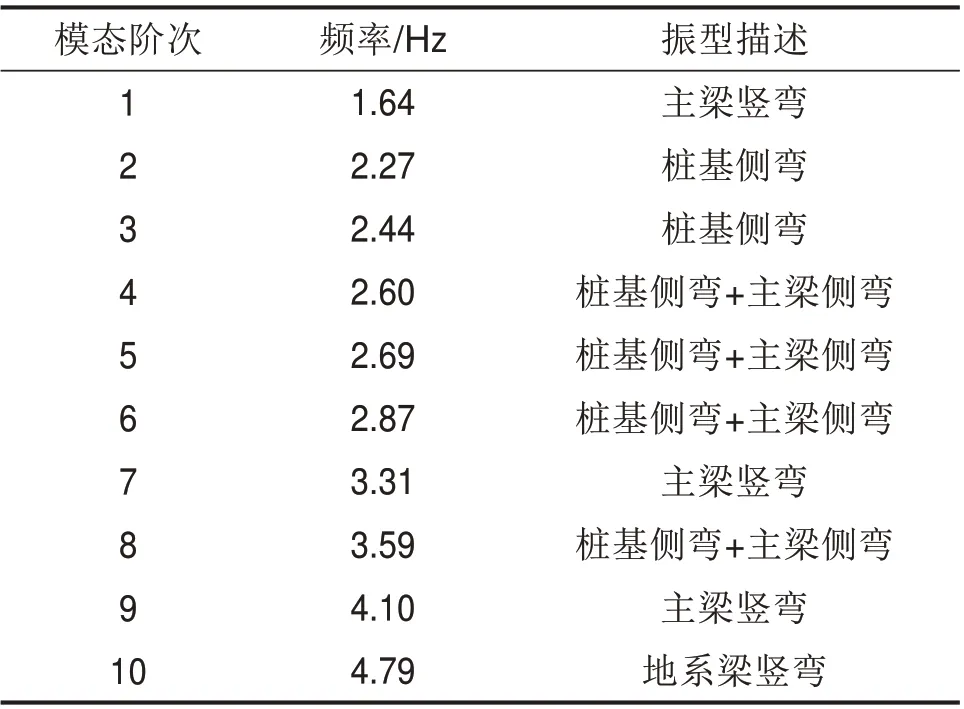
表2 模态频率及振型特征Table 2 Modal frequency and modal characteristics
从表2可知,本桥模态1,7和9以主梁竖弯振动为主,且模态频率在1.25~4.6 Hz 范围内,需要对这3 阶模态进行人致振动响应验算,3 阶模态的振型如图9 所示。本桥主梁侧弯模态的频率不在0.5~1.2 Hz 的范围内,故不需要验算侧弯模态的人致振动响应。
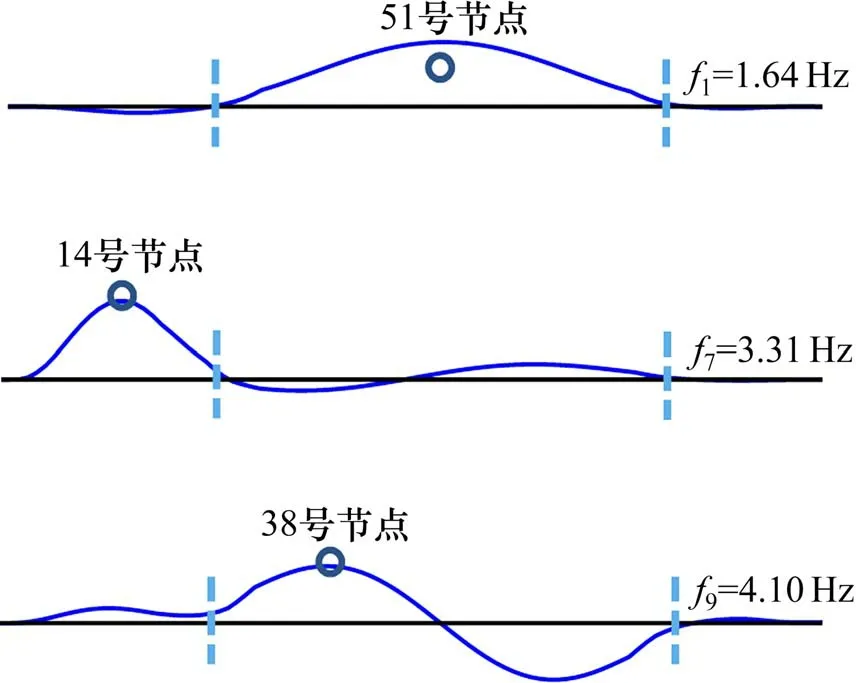
图9 主梁模态振型图Fig.9 Mode shapes of footbridge deck
3.3 人致振动响应
本桥桥面宽为5.0 m,桥长130 m,人群密度取1.0 P/m2,桥上行人总数为650 人,根据式(4)计算得到用于人致振动响应分析的每平方米等效行人数为0.072 6人。基于德国EN03规范,将人群荷载依据模态阶次分别加载到有限元模型进行动力时程分析,钢结构部分的材料阻尼比设置为0.004,混凝土部分的材料阻尼比设置为0.013[1]。计算时长为60 s,此时桥梁加速度响应已进入稳定状态。计算得到桥梁相应于各阶模态的的模态位移最大点加速度响应时程如图10~12所示。

图10 人群竖向荷载频率为1.64 Hz时的51号节点加速度响应时程Fig.10 Acceleration response time history of node 51 while vertical load frequency of crowd is 1.64 Hz
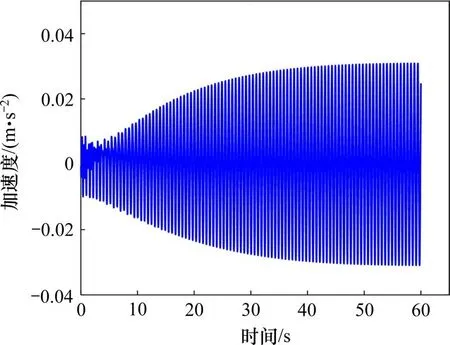
图11 人群竖向荷载频率为3.31/2 Hz时的14号节点加速度响应时程Fig.11 Acceleration response time history of node14 while vertical load frequency of crowd is 3.31/2 Hz
从图10~图12可以看出,当加载到桥梁的人群竖向荷载频率分别为1.64,3.31/2 和4.10/2 Hz 时,桥梁进入稳定状态后的最大加速度响应分别为4.349,0.031 和0.013 m/s2,模态7及模态9对应的人致振动舒适度等级达到CL1 级的要求,而模态1对应的人致振动舒适度等级不满足CL1~CL4的要求,此时桥梁发生大幅人致振动的风险比较大,需要采取减振措施以控制模态1对应的人致振动加速度响应。
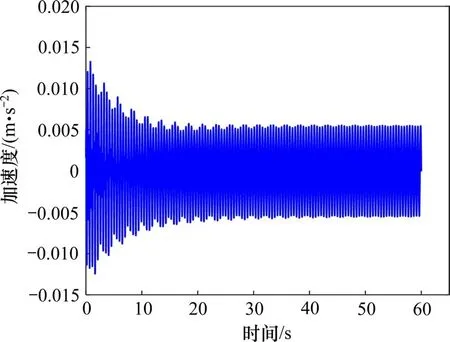
图12 人群竖向荷载频率为4.10/2 Hz时的14号节点加速度响应时程Fig.12 Acceleration response time history of node 38 while vertical load frequency of crowd is 4.10/2 Hz
4 减振设计
4.1 调谐质量阻尼器参数设计
对于如图13 所示的单自由度结构,在外荷载f(t)作用下。结构-TMD系统的运动方程为

图13 主结构-TMD 系统简化力学模型Fig.13 Structure-TMD system simplified mechanical model
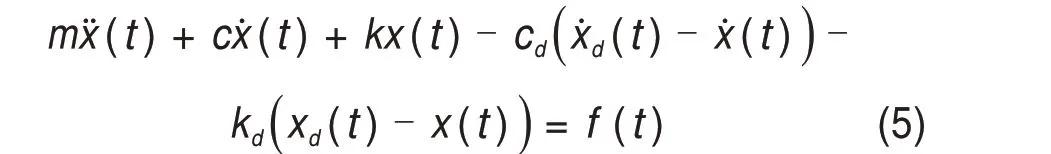
式中:m,c和k是主结构的质量、阻尼和刚度;md,cd,kd为附加结构的质量、阻尼和刚度。ẍ,ẋ,x分别为主结构加速度、速度和位移;ẍd,ẋd,xd分别为附加结构(即TMD系统)的加速度、速度和位移。
人致振动控制是以最小化加速度为控制目标,且行人对桥梁结构的荷载可近似为简谐荷载,基于此假设,对式(5)进行最优值计算,得到调谐质量阻尼器的最优频率和最优阻尼比为[11]:
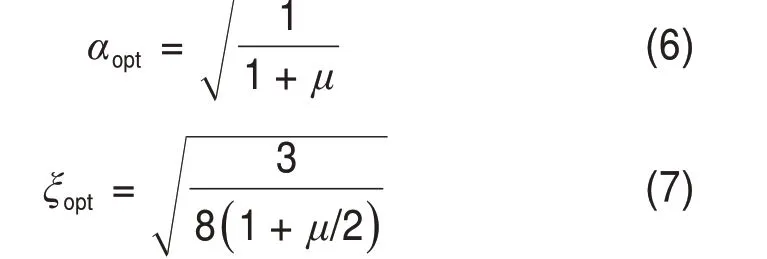
αopt为TMD 的频率与主结构频率之比的最优值;ξopt为TMD 的最优阻尼比;μ为TMD 的质量与主结构的质量比值。
从式(6)~(7)可知,TMD 的最优频率和最优阻尼比均与质量比直接相关,调谐质量减振系统设计的第一步便是通过试算确定拟用的质量比。工程中常用的调谐质量阻尼器质量比范围一般取1%~5%。本文计算了不同质量比情况下桥梁的竖向最大加速度响应,其中人群动力荷载的加载时间为60 s,确保桥梁加速度响应进入稳定状态,统计汇总的桥梁稳定后的竖向最大加速度响应如图14所示。
从图14 可知,当质量比达到0.5%以上时,本桥在人群荷载作用下的最大加速度响应小于0.5 m/s2,满足EN03 规范中的CL1 等级要求。考虑到本桥位于人流密度大的市内休闲公园,对舒适度的要求高,本桥最终选用质量比为2%。
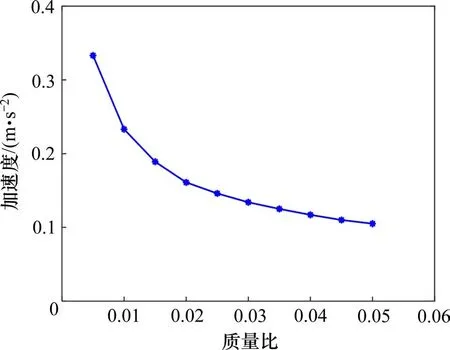
图14 质量比与桥梁最大加速度的关系Fig.14 Relationship between mass ratio and maximum acceleration of bridge
本桥模态1的模态质量为78 373 kg,在质量比为2% 的条件下,TMD 的质量为78 373×2%=1 567.46 (kg);依据式(6)同时考虑到本桥模态1 频率为1.64 Hz,计算得到TMD 的频率比为1.624 Hz;依据式(7)计算得到TMD的阻尼比为0.086。
基于上述TMD 参数,重新验算桥梁在1.64 Hz人群荷载频率下的加速度响应,计算表明,安装了TMD 之后,大桥模态1 对应的最大人致振动加速度响应降为0.161 m/s2。图15 给出了本桥有、无TMD2个工况下的人群荷载加速度响应时程曲线。

图15 人群竖向荷载频率为1.64 Hz时的51号节点在有、无TMD条件下的加速度响应时程Fig.15 Acceleration response time history of node 51 with and without TMD while vertical load frequency of crowd is 1.64 Hz
调谐质量阻尼器也叫动力吸振器,其减振效果对TMD 的频率非常敏感。实际生产制造过程中TMD 的频率与最优频率难免存在偏差,为了评估频率偏差对TMD 减振效果的影响,本文计算了质量比为2%且阻尼比为固定最优值的情况下,桥梁的最大加速度响应随TMD 频率偏差的变化情况,结果如图16所示。
其中:

从图16 可知,当TMD 的实际频率相对于最优频率有偏差时,调谐质量减振系统的减振效果将急剧降低。因此,减振系统实际实施时,考虑到桥梁实际频率与理论计算频率之间不可避免地存在偏差,应当以实际测试得到的桥梁模态频率作为确定TMD 频率的最终依据,从而确保减振系统对人致振动风险控制的有效性。
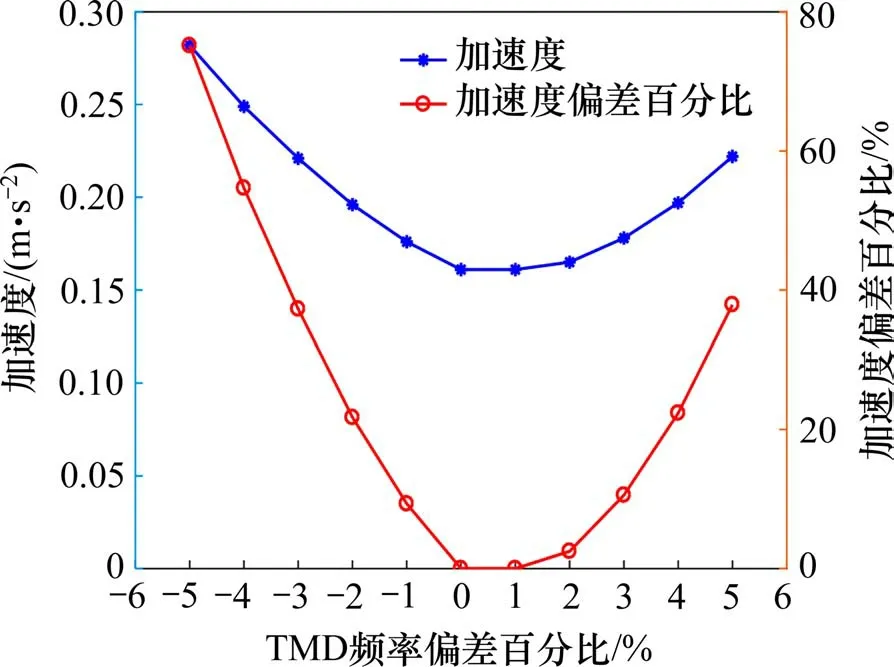
图16 桥梁的最大加速度响应随TMD频率偏差的变化情况Fig.16 Variation of maximum acceleration response of bridge with TMD frequency deviation
5 结论
1) 在人群荷载作用下,跨径布置为35+75+20 m 的斜腿刚构曲线连续梁人行桥有3 阶竖弯模态的频率在竖向人致振动验算范围内;而侧弯模态的频率超出横向人致振动验算范围,不需要验算。
2) 在人群荷载作用下,桥梁振动的最大加速度响应达到4.349 m/s2,桥梁发生大幅人致振动的风险较大。
3)基于加速度响应最小化原则设计了TMD 减振系统,TMD 对大桥人致振动加速度响应的控制效果显著,在安装了TMD 之后,大桥模态1 对应的最大人致振动加速度响应由4.349 m/s2,降为0.161 m/s2,满足EN03规范的CL1舒适度要求。
4)当TMD 的实际频率相对于最优频率有偏差时,调谐质量减振系统的减振效果将急剧降低。减振系统实际实施时,考虑到桥梁实际频率与理论计算频率之间不可避免地存在偏差,应当以实测桥梁模态频率作为确定TMD 频率的最终依据,以提高减振系统对人致振动风险控制的有效性。
