与J. Cahn 教授相关的材料学基本概念
2021-10-20供稿杨平
供稿|杨平 /
作者单位:北京科技大学材料科学与工程学院,北京 100083
提到材料大师Cahn,首先要弄清楚我们要讲述的科学人生故事的主人公是Robert Cahn 还是John W. Cahn。英国剑桥大学的Robert Cahn 的主要贡献是编著了称为材料领域“圣经”的《物理冶金》(Physical Metallurgy),并修改到了第4 版(1995 年),后期又出版了《走进材料科学》(The Coming of Materials Science)一书。而我们的科学人生故事主人公John W. Cahn 先后任职于美国麻省理工学院(MIT)、美国国家科学技术研究院NIST(前身为美国国家标准局NBS)。
如果问及学习过材料科学基础这门课程的学生:有哪些与J. Cahn 有关的概念或现象?估计大多数同学都回想不起来。但如果问及“调幅分解”这个基本概念,多数同学都会回想起来,这是因为这个概念涉及的相变形核过程非常特别,并且与“上坡扩散”概念相关联,容易给人留下深刻印象。表面上J.Cahn 的名字在材料科学基础课程中出现的并不多,但研究相变的教师及科研人员无不敬佩J. Cahn 对材料科学领域各个方面的丰硕贡献,材料科学基础课程中的不少基本概念均与他相关,只是没有像“Cottrell 气团”或“Frank-Read 源”那样直接使用科学家的名字命名相关的概念而已。
J. Cahn 对材料和数学领域做出了具有深远影响的成就。他应用热力学基本定律描述并预测大量的自然现象,是Gibbs 之后在热力学领域的权威。J.Cahn 在相转变和相扩散领域有关热力学及动力学的开创性工作、界面现象,以及与D. Shechtman 等一同发现准周期晶体(现在的“准晶”)等成就,使他为世人所知。J. Cahn 在1998 年获得美国总统克林顿亲自颁发的国家科学奖。同年,美国TMS 出版了J.Cahn 论文精选集[1],结合维基网站提供的其生平(http://en.wikipedia.org/wiki/John_W._Cahn),可以较清楚地了解其学术贡献。本文仅结合自己所讲授的材料科学基础课程,整理他的成果体现在哪些材料科学基础课程相关基本概念中,以强化学生加深理解,提高学习兴趣。在材料科学基础课程讲授的基本概念中,他贡献的学术理论相对复杂,涉及很多数学推导,且较为现代。相关的概念有:(1)相变动力学方程的修正;(2) 不同晶界位置的形核理论;(3)固态相变时位错形核理论;(4) 调幅分解理论;(5)有序-无序转变中的调幅分解理论;(6)杂质钉扎晶界迁移理论。此外,块形转变、准晶等也与J.Cahn 有关。
J. Cahn 教授的生平简介[1]
1928 年J. Cahn 生于德国科隆(图1),其父亲在纳粹掌握政权之前从事过反对纳粹的民事律师事务,因受到纳粹的追捕而逃离德国并移民美国。J. Cahn 于1949 年获得了密歇根大学(University of Michigan)化学专业的学士学位,1953 年获得加州大学伯克利分校的物理化学专业博士学位。1954 年加入位于纽约斯克内克塔迪(Schenectad) 的通用电气(GE)实验室跟随D. Turnbull 开始化学冶金学的研究。当时Turnbull 已经完成了有关形核动力学的前期工作,整个研究小组将重点放在固态相变的动力学与热力学的研究上。J. Hollomon(热变形中的Zener-Hollomon 参数以他的名字命名)则是GE 公司研究所的负责人。J. Cahn 还在芝加哥大学金属所的C. Smith(主要研究晶粒间的拓扑学关系) 领导下工作过。

图1 J. Cahn 照片
1964 年J. Cahn 成为麻省理工学院冶金系(现在的材料科学系)的教授。1969 年J. Cahn 与他的研究生F. Larché开始研究机械应力对固体热力学的影响。J. Cahn 的方法奠定了应力作用下的材料热力学研究基础,给出共格析出相周围区域或是位错周围应力区的热力学解释。1972 年J. Cahn 与D.W.Hoffman 合作建立了基于矢量的热力学理论去描述界面处的热力学过程,该理论对各向异性材料非常有用,这就是后来的界面能毛细管效应矢量方程。1975 年J. Cahn 与他的研究生S. Allen 开始对铁合金的相变过程进行了研究,包括有序-无序相变,并推导出了Allen-Cahn 方程。1984 年他成为了华盛顿大学的教授。由于其夫人是当时卡特政府的官员,他成为美国科学关键机构——国家科学与技术研究所(NIST)的成员。1977 年进入国家标准局NBS(NIST的前身) 材料科学与工程实验室时是访问教授,1984 年后成为高级教授。1982 年Shechtman 观察到准晶时,J. Cahn 建立了理论说明这种新结构具备热力学稳定性,并且成为准晶这篇经典文章的合著者。
J. Cahn 于1998 年在他70 岁时获得美国国家最高科学奖章,克林顿总统在白宫典礼上授予了他和其他8 位获奖者奖章。国家科学奖章是美国最高的科学奖项,J. Cahn 为NIST 第一个获得此奖章的科学家。
J. Cahn 是美国国家科学院、国家工程院和美国艺术和科学院院士,在40 年的职业生涯中,发表了250 多篇科学著作,做了400 多场特邀报告,并在国际上取得了数不清的荣誉。在纪念J. Cahn 教授70 岁生日时,组织者出版了一个J. Cahn 论文精选集,由J. Cahn 的30 篇代表作组成的经典文章汇编而成(图2),其封面背景图就是“调幅分解组织演变图”,并且每篇文章都附有一个对其工作非常了解的知名专家给出的导读[1]。论文精选集的序言是这样评价J. Cahn 的贡献的:冶金学家认为其贡献在相变热力学、相变动力学、体视学、调幅分解、共格应力、凝固等方面;陶瓷学家因其在界面小面化转变、浸润力、杂质拖曳力理论上而熟悉他;晶体学家因其在准晶、晶界对称性上而了解他;数学家因Cahn-Hilliard 方程和Allen-Cahn 方程及动力学变量公式而熟知他;高分子学家利用Cahn-Hilliard 方程设计新型结构;物理学家因临界浸润、弥散界面、表面热力学、调幅分解概念的普适性而熟知他。

图2 J. Cahn 经典文章汇编首页
与J. Cahn 相关的材料学基本概念
J. Cahn 对相变动力学J-M-A 方程的修正与地点饱和形核概念的提出
相变动力学Johnson-Mehl 方程是学生最熟悉的新相转变量与时间的定量关系。其应用的条件是均匀形核、形核率与长大速度是常数。但对于固态相变来说,非均匀形核是其主要特点,形核率也会随时间变化。Avrami 方程修正了应用条件,形核为非均匀的,且形核率随时间成指数变化且有位置饱和。J. Cahn 等[2]在研究珠光体分解中提出“地点饱和形核”的概念,认为这些有效的晶界核心地点被珠光体占满后(大约是转变量的20%~30%),形核率就不起作用,只有长大速度的影响了,并推导出对应的晶界形核、晶棱形核与角隅形核下三种动力学转变量与时间的关系式。这些公式后来被英国牛津大学教授J. Christian[3]总结在转变动力学表中并引入教材(见材料科学基础教材第10 章相变原理中的表2),其特点是晶界二维地点形核,Avrami 方程时间t指数n由4 降为3,晶棱一维地点形核使n降为2,角隅零维地点形核使n降为1。这些公式既适合相变,也适合再结晶。
J. Cahn 的晶界不同位置形核率相对贡献的理论
J. Cahn 于1956 年定量计算了上述晶界面、晶棱边、角隅三种不同的晶界形核位置形核率相对难易及晶粒尺寸D/δ(晶粒直径与晶界厚度)与新相浸润程度k(k=2cosθ,θ是浸润角) 对各类形核率的影响(图3)[4]。参数A为不同地点形核功与晶内均匀形核功的相对比值(ΔFi/ΔF*0),由图3(a)可见角隅上形核比晶棱上形核容易,而晶棱形核又比晶界形核容易。图3(b)则表明新相的浸润能力越差,即cosθ越小,大尺寸晶粒中均匀形核作用越大。在J. Cahn 论文精选集中[1]对该文的导读中,Purdy 教授指出晶界形核理论是对晶内形核的Johnson-Mehl 方程的延续,强调了不连续性。珠光体分解理论的经典文献是晶界形核理论的一个很好的应用案例。

图3 不同形核位置的相对形核功与新旧相浸润角(k=2cosθ)的关系以及晶内或晶界不同位置形核获得最大形核率时的A 和k 范围[4]
J. Cahn 的位错形核理论
J. Cahn 于1957 年计算了固态相变时位错上形核的临界形核功及临界半径[5],见图4(a),确定了形核过程中的两种临界状态,即位错富集溶质原子局部能量最低的气团状态(图4(b) 中αD>-1 曲线的峰谷位置,αD是和新旧相自由能差、比表面能、切变模量有关的参数) 和形成一个核心的临界状态(图3(b)中αD>-1 曲线的峰位置)的能量变化规律。固态相变的典型特点是缺陷处形核,除面缺陷界面处形核外,人们自然联想到线缺陷位错上的非均匀形核。实际金属材料生产中都经过热轧、热锻等工艺,晶粒内部存在大量位错缺陷。

图4 位错上形成的新相核心形状示意图(a)及位错上形核时形核自由能ΔG 与核半径r 的关系(b)[5]
相变分类法——Gibbs 方法的延续
相变种类繁多,其分类方法也很多,如:(1)按热力学参数分类的Ehrenfest 法;(2)按相变成分涨落过程是否连续的方式分类的Gibbs 法;(3)按原子以“平民式”扩散还是“军队式”切动迁移方式分类的Frank 方法(或Buerger 方法);(4)按相变时界面滑动和非滑动的Christian 相变分类法等。在Gibbs 相变分类法中引用的示意图来自J. Cahn 于1962 年论述调幅分解的经典文献[6],见图5。Gibbs 相变分类法将相变分为形核涨落型和连续转变型。形核涨落型相变的特点是小范围内的成分大起伏,连续转变型相变的特点则是大范围内的小起伏。由此出发,J. Cahn延续Gibbs 的热力学分类角度,引出了“弥散”的相界面概念,其定量表达式就是著名的Cahn-Hilliard 方程,后面的调幅分解理论便是该方程的应用。文献中常出现一个称赞学识渊博的Cahn 的叫法“Read Cahn”[1],因为前人曾称Gibbs 为Read Gibbs,大概指大师Cahn 的意思吧,也有人称Cahn 为Gibbs 第二。
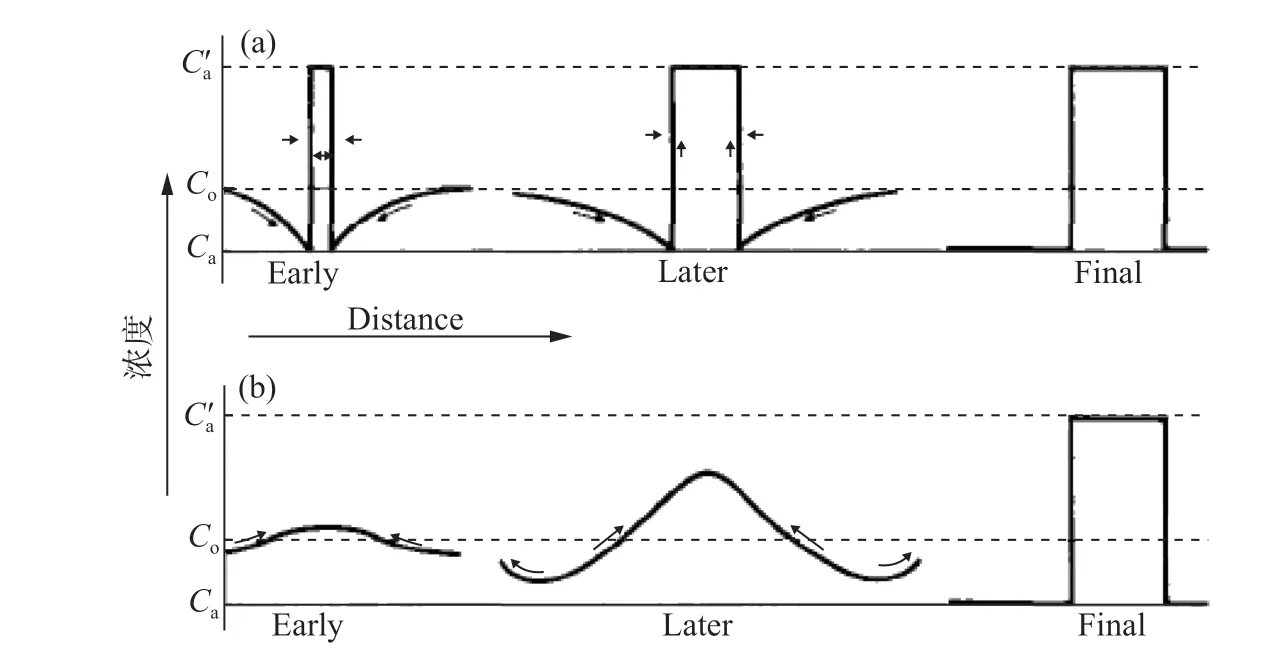
图5 调幅分解机制与形核长大差异的浓度变化图解: (a)形核长大方式的浓度变化;(b)调幅分解方式[6]
调幅分解与Cahn-Hilliard 方程
调幅分解为相变中连续型转变的一个例子,其特点是相变时在很大空间范围中原子发生轻微重排的涨落,在转变的早期成分分布为周期性缓慢变化的波,在相变的起始状态和终态之间存在一系列连续的状态,通过涨落连续地长大成新相。这是一种扩散型转变,但转变没有形核位垒。20 世纪50—60年代,J. Cahn 从最基本的Cahn-Hilliard 方程一般式(见式(1))出发,建立了基于动力学的扩散方程(见式(2)),最终给出方程的解,即成分与时间和位置的关系式。图6 给出具有溶解度间隙的相图(a)、对应的自由能曲线(b)以及化学拐点与共格拐点并存的示意图(c)。这样,在考虑应变能时必须在共格拐点线之内才发生调幅分解,并且分解最终出现平衡产物的成分由共格溶解度间隙线决定。受篇幅所限,这里尽量简化文字,详细描述可参考教科书或原著[6-9]。
图6 固溶度间隙相图(a)、自由能曲线(b)和相图中对应的化学拐点线和共格拐点线(c)[6-9]

此外,有文献这样评述:1958 年Cahn 和Hilliard在对两种混合液体(我们的材料科学基础教材内是固溶体)或气体分子之间的扩散渗透现象进行研究时提出的这个方程,在后续研究过程中发现该方程还可以用于研究生物群体动力学和社会学之间的种群相互竞争、人口学和社会学中的人口迁移扩散、固体液体混合表面的相互渗透等种种扩散现象。在应用方面,Cahn-Hilliard 方程在气体动力学、气动声学、叶轮机械、湍流、采油模拟、浅水造型、天气预报、多孔介质中的污染物运输、流体力学、渗透动力学等领域近年来有着越来越广泛的应用。
有序-无序转变中的调幅分解
在固溶体的有序-无序转变中也会出现调幅分解。材料科学基础教材中介绍以二级相变方式的有序-无序转变时给出Soffa 和Laughlin(J. Cahn 的博士生,卡内基梅隆大学Alcoa 教授,第5 版《物理冶金》书籍的主编) 以有序相和无序相的吉布斯自由能-成分曲线来说明调幅分解的示意,如图7 所示。图7(a)显示无序相不会发生调幅分解,其转变为有序相后会发生调幅分解。图7(b)表示无序相与有序相都会发生调幅分解过程。这些图来自1982 年Soffa 和Laughlin 在固态相变国际会议上有序-无序转变综述文章中的示意图[10]。而其参照的工作是Allen 与Cahn 于1976 年研究Fe-Al 有序合金中得出的[11],图7(c)~(f) 为原文中的图。参照图7(c) 中的Fe-Al 相图的局部相图和图7(d)~(f)的自由能-成分曲线可见,在高温T1下,高温BCC 结构的无序相α 和低温有序相都不会发生调幅分解(图7(d)),C1λ点右侧成分合金会发生二级相变直接通过原子跳动完成无序→有序转变(有序相与无序相之间没有两相区);T2温度时(称为三线交界的临界点),高温无序相和低温有序相也都不会发生调幅分解(图7(e)),点右侧成分合金还是以二级相变方式直接完成无序→有序转变;低温T3温度下(图7(f)),在有序相自由能曲线的两拐点成分(C3λ~C3s)以内的合金,在完成无序(上侧曲线) 向同成分的有序相(下侧曲线)二级相转变后,有序相再进行调幅分解,连续变成成分为C3α的α 相和C3B2的B2 有序相,这个过程是一级相变,无序相与有序相之间存在两相区。可见,这是个非常好的复习相图理论、有序-无序转变理论(一级或二级相变) 和调幅分解(一级连续式相变)理论的综合能力的案例。类似地,Fe-Si 合金也有相似的有序-无序转变,这是两个典型的涉及有序相的常用合金。

图7 Soffa 和Laughlin 于1982 年给出的有序-无序转变自由能关系示意图(a,b)和Allen、Cahn 于1976 年给出的Fe-Al 合金有序-无序转变方式、温度与成分的关系(c~f)
与Cahn-Hilliard 方程同样在数学界有重要影响的是Allen-Cahn 方程。Allen-Cahn 方程是二阶非线性的(Cahn-Hilliard 方程是四阶偏微分方程),最初是两人研究固相反相畴界运动及反相畴粗化时提出的[12]。其形式见式(3)和式(4)。它们与Fick 第二定律扩散方程形式给出的式(2)有些相似,其中η是有序参量,Δf0是单位体积自由能变化,M与扩散系数有相同量纲,κ是梯度能系数,α是动力学参数(M=2ακ),g是界面法线方向距离参量。K1+K2是界面平均曲率。Allen-Cahn 方程除了描述微观扩散理论中弯曲反相畴界运动外,在材料流体动力学和反应扩散问题中有着广泛的应用,如可浸液体中的粗化动力学、晶体生长、人群扩散现象、随机扰动和图像处理问题等。

杂质钉扎晶界迁移速度的Cahn 理论与Lücke 理论
溶质原子因产生畸变而提高系统自由能,为降低能量,它会偏析到晶界上而稳定下来,并对晶界的迁移产生阻碍作用。目前使用的材料科学基础教材(2006 年版)中引用的是德国亚琛的Lücke 教授于1957 年和1971 年的文章[13-14]中溶质在晶界附近的分布和溶质浓度对迁移晶界作用力的关系曲线,见图8(a)和8(b)。然而在早期教材《金属学原理》(余永宁编,2000 年版) 中曾引用J. Cahn 在1963 年发表的作用在晶界上的力与溶质浓度和迁移速度的公式,见式(5) 和式(6)[15]。P是作用在晶界上的驱动力,Pi是杂质拖曳力,V是迁移速度,C0是杂质浓度,α、β是与温度、扩散系数、交互作用能有关的常数;λ是与本征拖曳系数有关的常数,与本征迁移率成反比。图8(c)~(e)给出J. Cahn 发表的动、静态下晶界处溶质浓度、能量、所受阻力的曲线,可见其相似性。特别应说明的是,J. Cahn 和Lücke 不同杂质含量下对应的作用在晶界上的总力与迁移速度的关系图表面上差异较大(见图8(b)和(e)),但实际正好是x-y坐标的颠倒,即本质是一样的。图8(e)的横坐标为迁移速度,纵坐标为作用在界面上的力,图8(b)则相反。相关理论分别称为晶界迁移的Lücke理论和Cahn 理论。图8(d) 给出不同迁移速度的晶界上溶质原子的分布情况与图8(a)中下面c-x图对应。随晶界迁移速度的提高,晶界富集程度越来越小。

图8 溶质偏析钉扎晶界的Lücke 模型(a,b)与Cahn 模型(c,d,e)


Cahn 与准晶发现者Shechtman
准晶的发现主要是以色列材料学家Shechtman于1982—1984 年完成的。在J. Cahn 的推荐下,Shechtman 于1981—1983 年在Johns Hopkins 大学作为双聘研究人员,共同完成NBS(美国国家标准局是Cahn 工作的机构) 资助下的铝-锰合金激冷组织研究,发现了二十面体准晶,突破了传统晶体学的限制,开辟了新的材料研究领域,以此经典文献[16]Shechtman 获得了2011 年化学诺贝尔奖。Shechtman 发表在Physical Review Letters(PRL)期刊中的经典准晶文章[16]中的作者还有以色列学者Blech,法国CNRS冶金化学研究所的D. Gratias(我的大学同学张葵教授的导师,张葵教授现任教于法国某大学) 和美国NIMS 的Cahn。图9 照片中后排站着的就是J. Cahn,从左边数第3 位是D. Gratias。如同两次诺贝尔奖获得者L. Pauling 的观点一样,J. Cahn 起初对准晶的衍射数据也持怀疑态度,认为5 次衍射斑的对称性来自多重孪晶[1]。我国从事准晶研究的学者也在中文书籍[17]中介绍了当时的场景。的确,准晶中20 面体原子堆积的衍射斑与多重孪晶太相似了,而Pauling有着丰富的多重孪晶衍射斑分析的实际经验,才将其误认为是多重孪晶。在这项晶体学方面的工作中J. Cahn 虽然没有对直接获得准晶衍射斑起作用,但在推动准晶理论、与Pauling 在Nature刊物上的学术争论等方面做出了贡献。文献[17]中详细介绍了J. Cahn 帮助D. Shechtman 找到法国晶体学家D.Gratias,从理论上揭示出准晶的结构特点,并且帮助他在JAP退稿后改变策略,突出重点,最终顺利在PRL上及时发表的科学故事。其推动作用见J.Cahn 作为第一作者发表的一系列准晶理论文章[18-24],例如对20 面体(Frank-Kasper 多面体)准晶内原子占位的分析,用六维晶体学参数(或空间)及Patterson函数确定了准晶中Al-Si-Mn 原子的位置[24]。

图9 Shechtman 与同事讨论晶体结构(左侧站立者为Shechtman,后排中间站立者为J. Cahn)
对科研与教学的思考
在总结我所讲授的材料科学基础课程中与J.Cahn 有关的基本概念或理论时,有如下几点体会:
(1)J. Cahn 的研究成果涉及材料领域的方方面面,宽而深入。读了J. Cahn 的代表作后,感觉他将各种基本过程的定性或半定量关系都更好地定量化了,全面提升了对材料基本过程的定量化描述。比如著名的J-M 方程需要均匀形核、球状核心的条件,Cahn 推导出了任意空间位置、任意形状的核的长大动力学关系式,特别是其Cahn-Hillirad 方程和Allen-Cahn 方程在数学界的影响,仅检索国内中文学术论文和学位论文,就可看到很多以解该方程为内容的研究。其热力学、动力学定量分析理论,即使作为教师也难以理解。由此引申到材料科学也还在不断发展中,涉及的内容很宽、很深,即使讲了几十年课程,我也未能真正理解透彻,需要活到老学到老。
(2)本文最重要的目的是将一些在教材中出现的与J. Cahn 的原始工作直接相关的基本概念或理论整理出来,这并不是一件很容易的工作。因为编写教材时可能参阅比较权威的、经过加工总结的综述或专著,这时原创作者的名字可能被忽略。当然有些理论也不好确定谁是最先做出的,并且教材内容的选取也没必要一定采用最先研究人员的结果。但不管如何,整理J. Cahn 的研究成果与课程基本概念的对应关系不仅是对大师的尊重,也锻炼了检索、分析、整理的能力。希望读者在查询、思索、归纳中体会到材料科学基础课程学习中的乐趣及课程知识的实用性,从中感悟到一些基本概念背后的有价值的东西,这些都是我们未来材料研究中将经历的过程。
(3)在我撰写的其他9 篇类似的教研文章中,本篇文章从素材收集上讲是最完备的,因为J. Cahn 的文章非常多,加上1998 年其生日纪念会TMS 出版的J. Cahn 精选论文集中的序言、生平和每篇文章的导读文章,素材非常多,因此本文应该也是最容易写的,但实际却是最难写的,撰写时间也最长。一方面其很多成果在材料科学基础教材中没有直接给出他的名字,加上其很多成果超出本课程授课内容范围,且许多是数学上的推导,不但学生难以理解,作为不从事其研究方向的教师也不易看懂;另一方面是我的科研方向与J. Cahn 的工作交集很少,长期科研的积累能提供的帮助很小。只有在确定再结晶晶粒长大速度时用到Cahn-Hagel 方程,这个方法在课程中还没介绍。现在的高校教师除教学外,都承担有大量的科研任务,以及其他的非教学与科研事务,没有足够多的时间来全面、仔细、深入理解并品味出Cahn 一生研究成果的来龙去脉。
(4)作为专业课教师,除了需要讲好课,将这些有趣的故事融入基本概念的介绍中以优化教学效果外,我们还面临教材更新的问题。不论原教材内容如何新,讲过5 年以上就应更新部分内容。随着材料表征技术的不断更新,模拟计算技术的更强大有力,以及实验研究的不断进行,以前对材料行为的定性和半定量规律逐渐转化为定量,数学、化学、物理学的定律关系越来越融入材料学。教师首先要消化、吸收,以恰当的方式引入新内容,删去一些过时的内容。其次,教材如何更新,需要在教研组范围、教学会议上、各级教学组织中不断讨论、协商。
结束语
通过本文的撰写,希望读者:或站在学生的层面上,将文中整理出的8 个与J. Cahn 相关的基本理论作为一个整体而强化对它们的理解;同时了解、认识J. Cahn 的精彩科学生涯、科研脉络、经典文章及其科学贡献;并提升或学会今后开展科研时对任一个方向的来龙去脉的查找归纳能力。或站在教师的层面上,将8 个基本概念作为一个有机的整体,构思出一个相互关联、系列有趣的故事去提升教学效果;在此基础上,总结J. Cahn 科研工作的特点、风格以及与其他大师如Hillert、Aaronson 并肩工作的密切联系与合作;抓住其“弥散界面”核心思想的精髓,以及由其延伸出的调幅分解、有序-无序相变与连续转变的理论,直至其全面的热力学、动力学、晶体学定量描述的能力。最后,作为专业课教师,面临教材更新的挑战以及不论讲授课程多少年,都需要不断学习、不断提升的历史责任。
致谢
感谢顾新福副教授帮助收集许多经典文献及有益的讨论和修改建议。
