子弹侵彻装甲钢板数值仿真分析

李孟华，马 治，桂堂军，彭 兵，李大禹

(1.驻沈阳地区军代局驻长春地区第二军代室，吉林 长春 130011) (2.一汽解放汽车有限公司，吉林 长春 130011) (3.南京理工大学机械工程学院，江苏 南京 210094)

随着军用暨特种车辆的更新换代，车辆防护安全性越来越被重视，车辆防护要求也越来越高。为了获取子弹实际侵彻能力并应用于防护车辆的设计过程中，需要对装甲钢板进行相应防护级别的射击试验，验证装甲钢板的防护能力。采用试验方法虽然能获得装甲钢板对不同子弹的防护能力，但需要准备试验设备、场地、试验品等，成本高、周期长；而计算机有限元数值分析技术可以作为快速、有效、方便的手段对各种工况的防护能力进行分析，指导越野车防护性能开发设计和轻量化设计。因此，如何得到与实弹射击相符的数值分析结果，即拟实化的结果，是子弹侵彻仿真分析的重中之重。

子弹侵彻装甲钢板是一个相当复杂的物理过程，涉及非线性材料本构、材料失效、结构大变形以及温度场变化等问题。材料参数是影响分析结果准确性的主要因素，为了获取高精度的数值仿真结果，一般都需要在开展材料试验时先拟合出材料本构参数，然后通过仿真修正材料参数，使有限元仿真结果与试验结果得以互相印证[1-2]。

1 有限元模型

由于子弹侵彻仿真属于高度非线性仿真，对网格质量要求较高，因此本文采用HyperMesh进行网格划分等前处理工作，利用LS DYNA进行求解计算，使用LS_PrePost开展后处理分析。

1.1 材料模型

子弹侵彻过程涉及材料高应变率、大变形、材料流动、材料断裂等物理现象，材料力学特性高度非线性，需要定义恰当的材料本构模型、失效模型及状态方程，常用的材料模型有双线性材料本构、Johnson-Cook材料本构[3-5]。文中材料均采用Johnson-Cook本构模型，7.62 mm普通钢芯弹的钢芯材料及装甲钢板材料参数见表1、表2[6-7]。表中：ρ为密度，c为比热容，E为弹性模量，ν为泊松比，A为初始屈服应力，B为应变硬化模量，n为硬化指数，C为应变率强化参数，m为热软化指数。

表1 钢芯Johnson-Cook本构模型参数

表2 钢板Johnson-Cook本构模型参数

子弹钢芯失效模型采用应变失效，最大失效应变为0.3；靶板采用Johnson-Cook累计损伤失效模型[8]，该模型是一种常用的描述不同应力三轴度、应变率及温度下材料的等效失效应变的模型，装甲钢板试验拟合得到的Johnson-Cook累计损伤失效模型参数见表3。

表3 钢板Johnson-Cook累计损伤失效模型参数

1.2 弹-靶模型

为了降低计算成本，且不影响求解精度，考虑到模型的对称性，数值计算模型采用二分之一对称模型。子弹模型按实物大小1∶ 1建立，从外到内依次为覆铜钢壳、铅套、低碳钢钢芯；靶板模型面内尺寸为200 mm×100 mm，厚度与实际靶板公称厚度一致。

7.62 mm普通钢芯弹及靶板网格均采用三维实体结构化网格，结构化网格整体质量高、求解计算稳定性好、求解精度高、沙漏能低。子弹网格基本尺寸为0.15 mm；靶板采用多尺度网格划分方法，靶板中心处面内网格基本尺寸为0.20 mm，厚度方向网格尺寸为0.25 mm，靶板边缘网格基本尺寸为1.50 mm。图1所示为7.62 mm普通钢芯弹侵彻4 mm靶板二分之一对称模型。

图1 7.62 mm普通钢芯弹侵彻4 mm靶板有限元模型

对靶板周边节点施加固定约束，对模型对称面处的节点施加对称约束，接触算法采用单面自动接触，动摩擦系数为0.1，子弹着靶速度与试验一致,为770.5 m/s，计算模型不考虑温度场变化。

1.3 数值仿真分析与试验

采用LS DYNA程序进行求解计算，可以得到7.62 mm普通钢芯弹100 m距离射击4 mm装甲钢板的侵彻过程，如图2所示。由图可知，4 mm装甲钢板被子弹穿透，不能抵挡7.62 mm普通钢芯弹的侵彻。

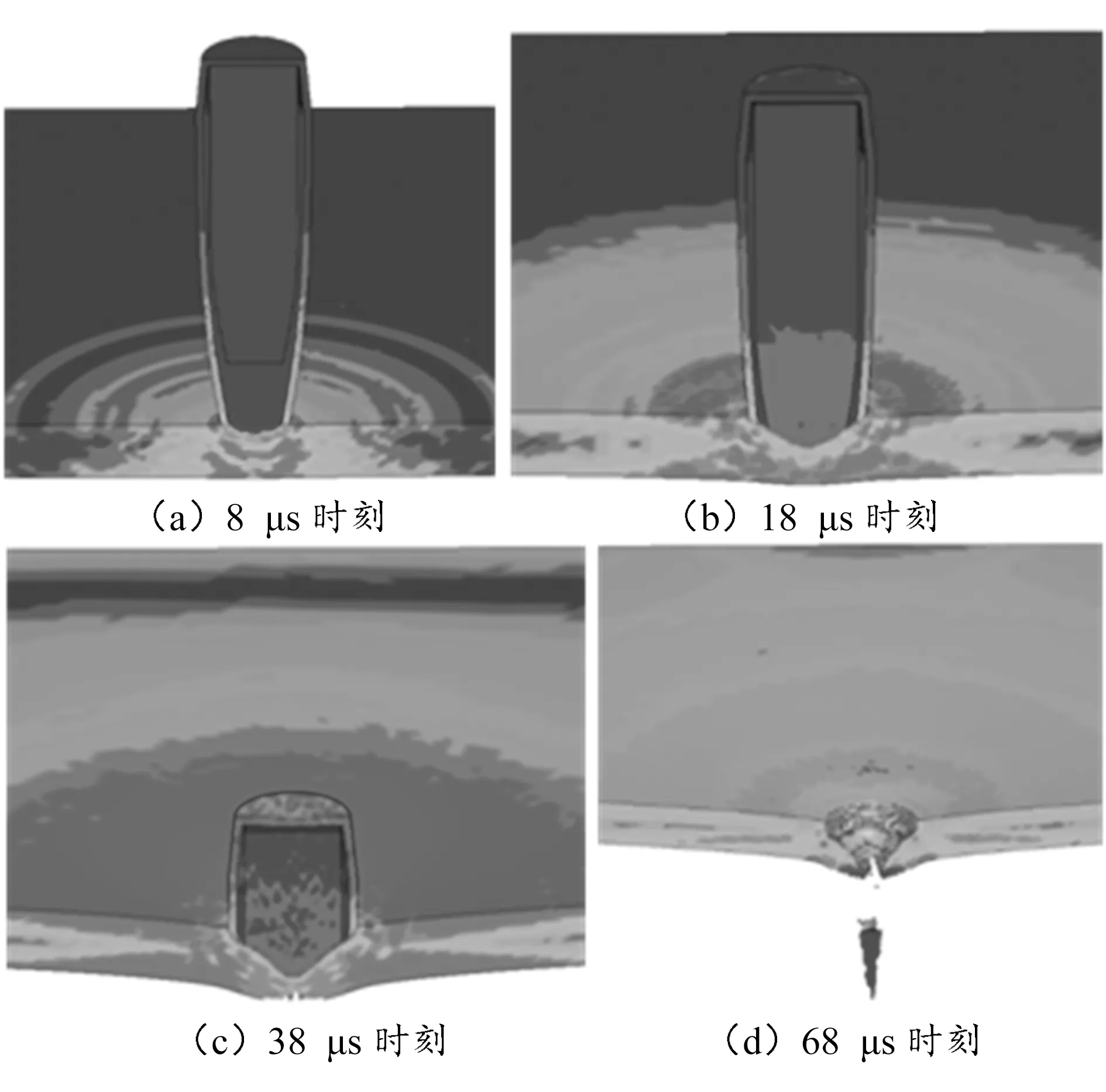
图2 7.62 mm普通钢芯弹侵彻4 mm靶板仿真过程

对4 mm装甲钢板进行100 m实弹射击试验，试验靶板长宽尺寸为400 mm×400 mm，射击角度为0°(垂直靶板面方向)，对试验后靶板进行光学三维数据扫描，靶板损伤状态如图3所示，靶板未能抵挡住子弹侵彻作用发生穿透，试验结果与仿真结果较近似。

图3 7.62 mm普通钢芯弹射击4 mm靶板试验结果

2 模型参数修正对标

从试验结果可以看出，4 mm钢板弹着点处底部发生了断裂和小穿孔，与仿真结果相似；但试验中弹坑为光滑过渡弹坑，仿真弹坑却呈非光滑状态，损伤状态差别明显。此外，数值模拟中子弹的钢芯在侵彻过程中侵蚀现象明显，而实弹试验中钢芯前端却因挤压镦粗出现开裂。因此为了提高仿真结果与试验结果的宏观形貌精度，需要对仿真模型参数进行修正。

2.1 材料模型参数修正

从图2中可知7.62 mm普通钢芯弹侵彻靶板时，靶板背面较早发生开裂失效，说明靶板失效应变和靶板强度偏小，需要适当调整失效模型参数：1)增大失效应变，将D1调整为0.45，并设置靶板最大拉伸应变为1.1；2)将靶板Johnson-Cook本构模型参数B调整为1 660 MPa。7.62 mm普通钢芯弹的钢芯材料为低碳钢，侵彻时主要表现为挤压失效，因此采用最大拉伸应变fs失效准则进行数值仿真，图4为钢芯不同极限拉伸应变的侵彻仿真结果。

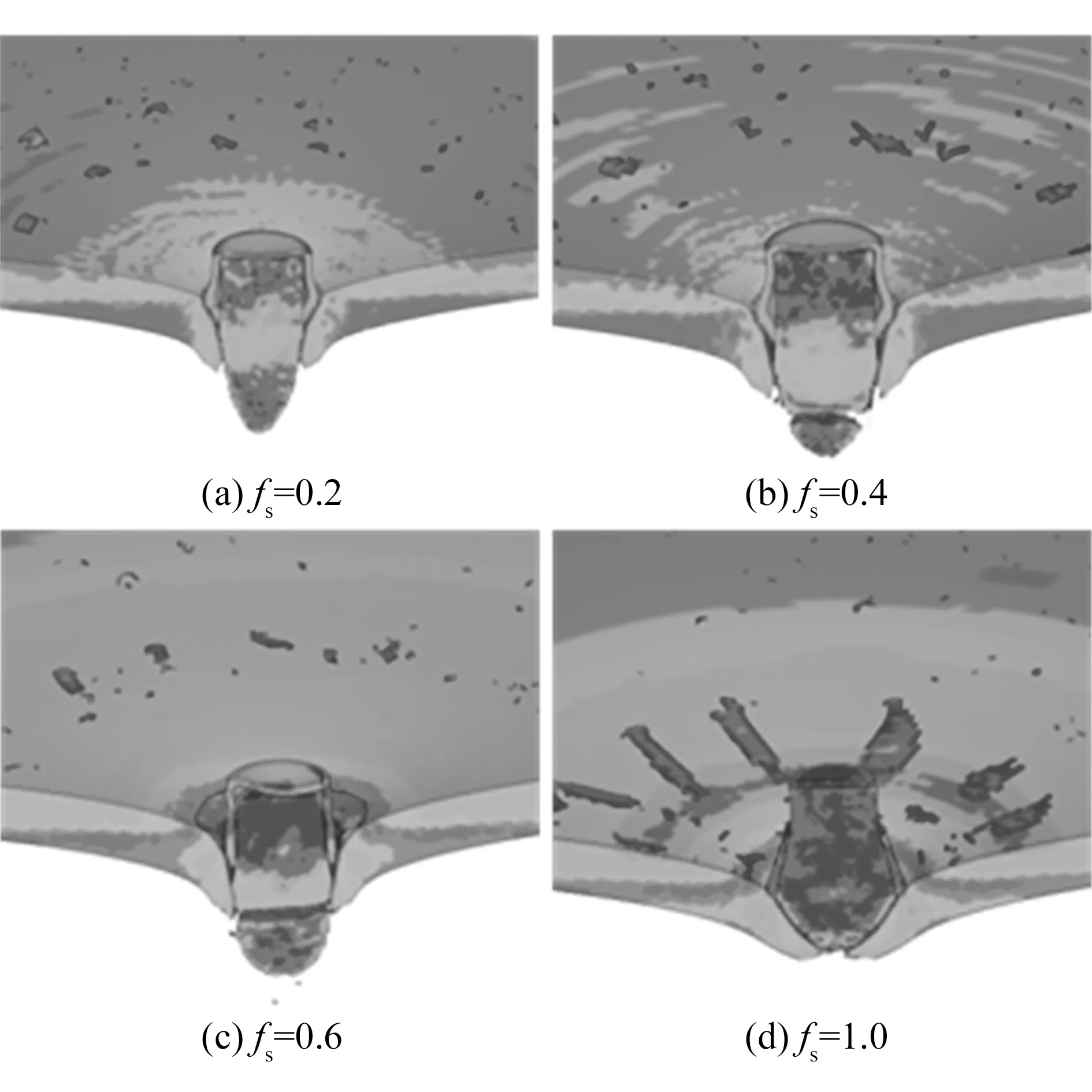
图4 不同极限拉伸应变下的仿真结果

将上述侵彻仿真分析结果与试验结果对比，可知7.62 mm普通钢芯弹钢芯材料拉伸失效应变设置为1.0时，仿真结果与试验结果基本一致，靶板弹坑与试验现象呈一致的光滑凹坑，大小相近，其不同时刻的侵彻过程如图5所示。

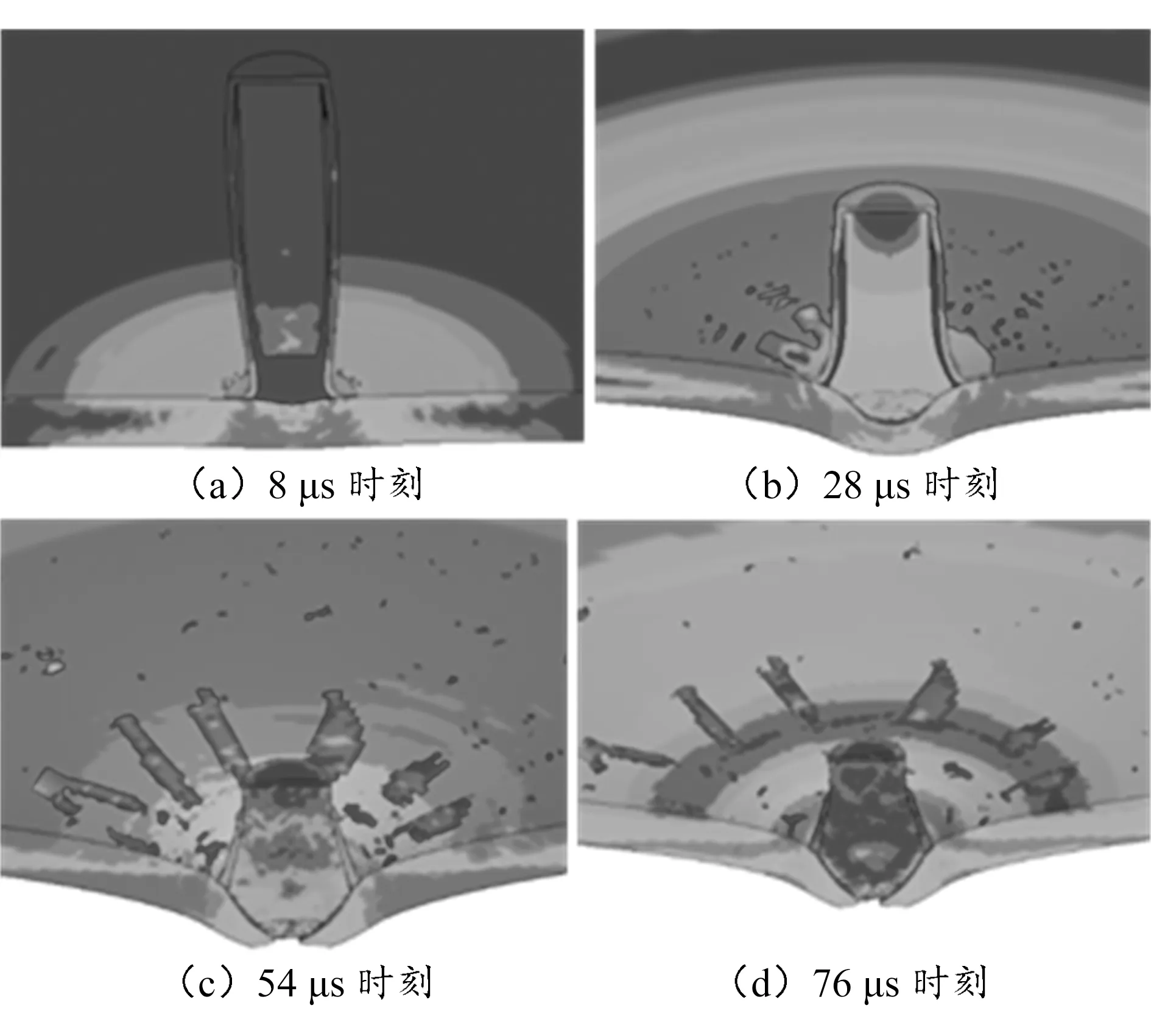
图5 子弹(fs=1.0)侵彻4 mm靶板过程

2.2 M80仿制弹侵彻仿真与试验

为了进一步验证2.1节中材料参数的可靠性，采用校正后的靶板材料参数，进行M80仿制弹的侵彻数值模拟，并与试验结果对比。其中，M80仿制弹为7.62 mm铅芯铜壳子弹。图6所示为M80仿制弹侵彻6 mm靶板的有限元模型及数值模拟结果，图7所示为M80仿制弹射击靶板试验结果，可以看出数值仿真中靶板未穿透，试验中靶板发生穿透，仿真结果与试验结果差距较大。

图6 M80仿制弹侵彻6 mm靶板的有限元模型及数值模拟结果

图7 M80仿制弹射击6 mm靶板试验结果

2.3 GISSMO损伤失效模型

从靶板射击试验结果可以看出，用7.62 mm普通钢芯弹射击4 mm装甲钢板时，钢板表现出较强的韧性，塑形变形较大，损伤失效主要表现为弹坑底部的裂纹扩展失效；而M80仿制弹侵彻6 mm装甲钢板时，钢板弹坑变形较小，损伤失效表现为明显的剪切孔，是主要由剪切应力应变导致的破坏。从宏观上看，两种侵彻工况失效现象有明显的区别；而从材料力学上分析，是两种侵彻工况失效处应力状态不同，失效的应变极限也不同。Johnson-Cook累计损伤失效模型表现为单调指数函数，对材料在不同应力三轴度下的失效描述不够精确，导致上述两种侵彻工况仿真计算不够准确。GISSMO损伤失效模型可以描述任意应力三轴度与等效塑性应变的关系，对材料失效描述更精确，能够得到更准确的仿真结果[9]。图8所示为不同损伤失效模型下应力三轴度和失效等效塑性应变关系曲线。

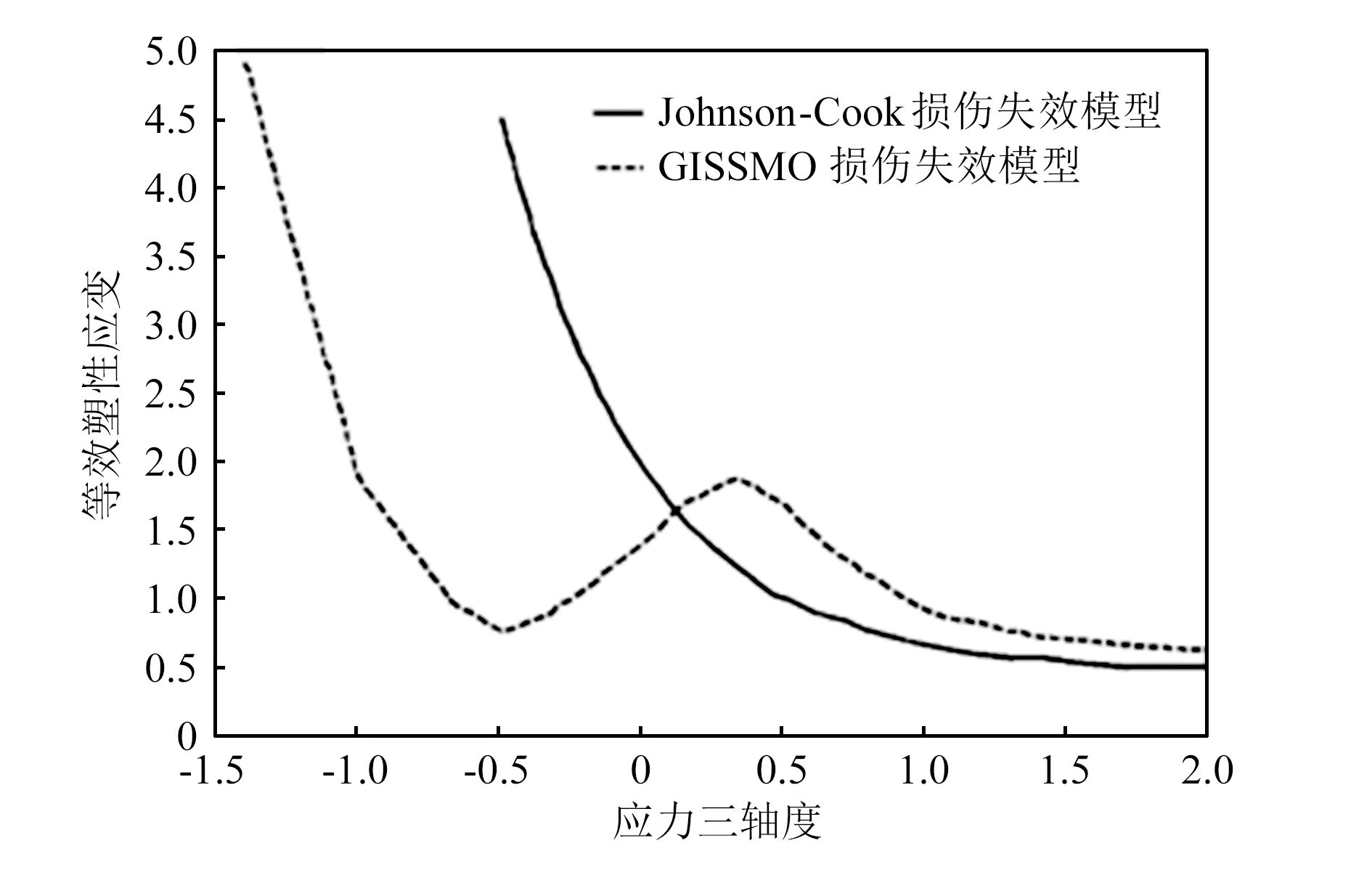
图8 应力三轴度和失效等效塑性应变关系曲线

采用GISSMO损伤失效模型开展7.62 mm普通钢芯弹和M80仿制弹侵彻仿真分析，仿真结果如图9所示，两种工况下仿真结果与试验结果均保持一致。

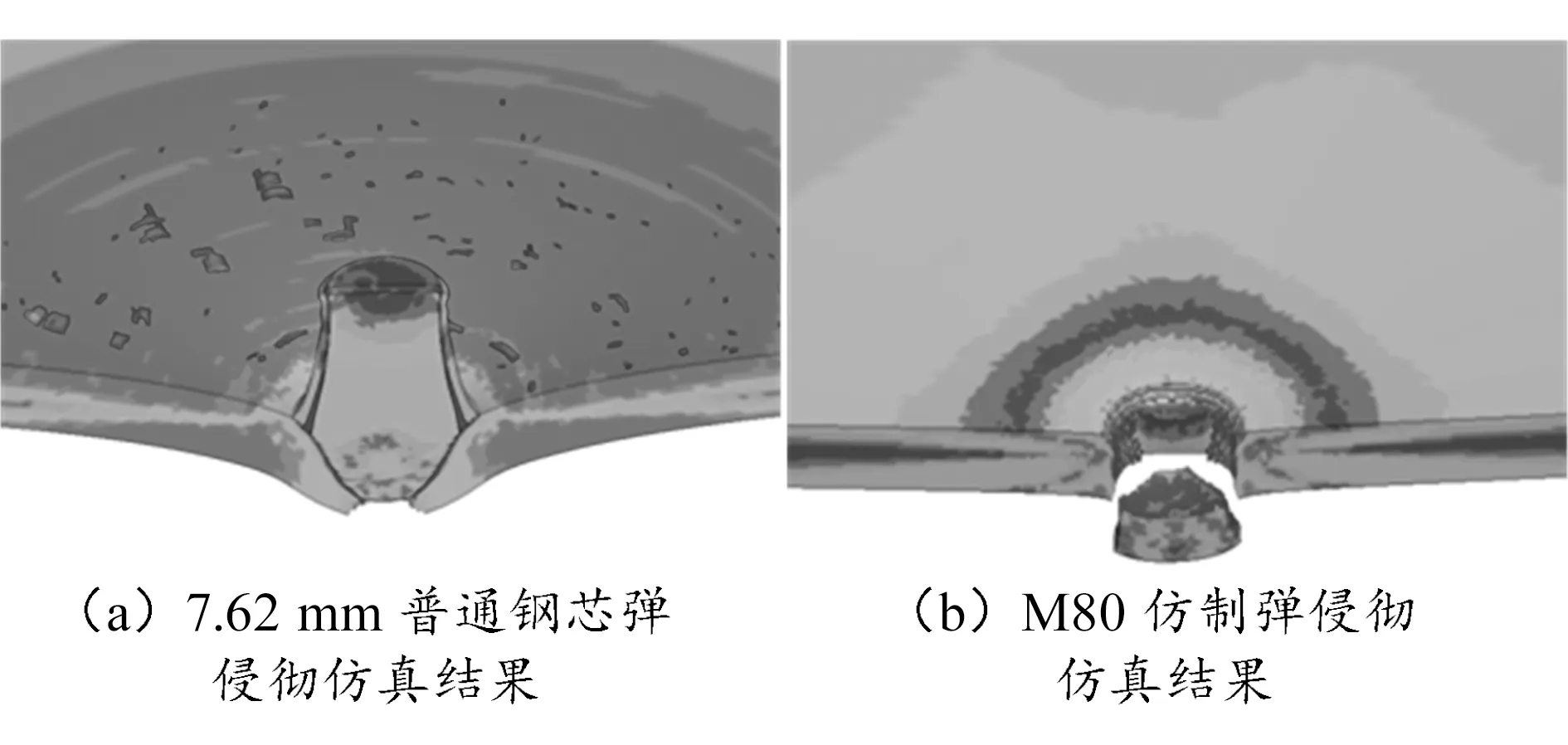
图9 GISSMO损伤失效模型仿真结果

3 结束语

本文通过数值仿真模拟与试验测试手段相结合，开展了7.62 mm普通钢芯弹和M80仿制弹侵彻防弹钢板的仿真与试验研究，探究了拟实化侵彻仿真模型参数的修正方法，得出以下结论：材料失效参数是侵彻数值仿真准确度的重要影响因素；针对子弹侵彻靶板的高速冲击复杂工况，Johnson-Cook累计损伤失效模型不能较好地模拟材料受剪状态下的失效行为；可通过增加GISSMO损伤失效模型来描述材料失效与应力状态等的关系，从而得到更准确的拟实化的仿真结果，为实际工程应用提供可靠指导。