基于大数据的K-means聚类算法的网络安全检测应用研究

李峻屹

(陕西警官职业学院 ，陕西 西安 710021)

互联网技术的飞速发展为人们带来了极大的便利，但与此同时也逐渐暴露出了一系列由于网络自身的设计缺陷、安全漏洞等因素引起的安全问题，而网络安全是一切应用程序得以平稳运行的保障与基础，因此对网络入侵检测技术提出了更高的要求。在此需求背景下，数据挖掘技术应运而生，利用各类算法对数据进行清洗与统计分析，充分挖掘出数据的潜在价值，为后续决策提供科学、合理的依据。聚类分析是数据挖掘中的主要分支，以数据的相似性作为依据完成数据划分，目前已经在机器学习、人工智能、网络安全等众多领域得到广泛应用。因此本文结合多种聚类分析算法的优点构建多级入侵检测算法，对入侵类型进行聚类分析与研究，为网络入侵检测提供技术支撑。

1 网络入侵检测现状分析

随着计算机和网络信息技术的不断发展与完善，网络空间中的数据量呈指数增长，最早Lee等在入侵检测系统中引入了数据挖掘技术，发现了用户和程序的特征模式，对入侵行为实现了有效的识别。目前入侵检测所使用的数据挖掘技术已经取得了一定的研究成果，包括基于朴素贝叶斯算法、SVM(支持向量机)算法、BP神经网络算法等多种数据挖掘算法[1]，但由于参数调整过于依赖人工、易陷入局部极小值、计算过程耗时长、检测精度较低等缺点导致整体入侵检测质量及效率均比较低。相对来说，聚类分析算法简单、复杂度低，在网络入侵检测中具备较高的适应性，其中较为常用的是K-means聚类算法，但该算法的聚类结果比较依赖初始簇中心点的选择，容易陷入局部最优解。因此在进行网络安全检测时，需对传统的K-means聚类算法进行改进与优化，力求提高入侵检测效率及准确性，降低误报率。

2 网络安全检测的设计

2.1 基于 PReLU激活函数的ELM算法

ELM算法(极限学习机算法)主要针对单隐含层前向神经网络，不需要迭代，随机产生的隐含层神经元阈值以及输入层与隐含层之间的连接权重向量显著简化了训练过程，只需设定隐含层的神经元数量即可，在学习速度、泛化性能等方面比传统算法更具优势。

ELM算法虽然可以满足入侵攻击分类的检测需求，但算法在选择激活函数方面存在较高的依赖性，激活函数的质量直接影响分类效果。传统ELM算法采用S型的Sigmoid函数作为激活函数，为了提升分类效果，引入基于核函数的极限学习机算法，将ELM隐含层的激励函数使用径向基RBF核函数代替，采用具有稀疏激活性的基于修正线性单元 PReLU激活函数，降低在深度卷积神经网络中的训练耗时。PReLU激活函数通过引入修正参数提升准确率，另外在考虑权重总数时可引入少量的额外参数避免过度拟合及额外风险，从而实现对ELM算法学习效果的优化[2]。

2.2 改进的K-means算法

2.2.1传统的K-means算法

K-means算法是一种迭代求解的聚类分析算法，预先将数据分为k组，随机选取k个对象作为初始的聚类中心，通过计算每个对象与各个聚类中心之间的距离将数据对象划分到距离它最近的聚类中心，每分配一个样本后重新计算聚类中心，不断重复直到满足终止条件。该算法可以在同一类中聚集较高相似度的样本，考虑到网络入侵检测时对算法复杂度的要求，在计算样本间的距离时通常采用算法复杂度较小的欧氏距离。

假设数据集D包含n个样本对象，每个数据样本的特征维度是m维，则第i个数据对象可以表示为Xi=(x1i，x2i，…，xmi)，其中xmi为数据对象Xi的第m维特征，i=1,2,…,n。随机抽取k个数据作为初始聚类中心，则第j个聚类中心可以表示为Cj=(c1j，c2j，…,cmj)，其中cmj为聚类中心Cj的第m维特征，j=1,2,…,k。则两个数据对象Xi和Xj之间的欧氏距离d(i,j)具体计算表达式如下[3]：

d(i,j)=

(1)

K-means算法的准则函数通常采用误差平方和函数，设Ci为聚类簇，Y为聚类空间的数据对象，mi为Ci的中心(即平均值)，则均方误差E可通过以下公式计算：

(2)

2.2.2基于距离阈值的K-means算法

在K-means算法中，不同初始聚类中心的聚类效果不同，不合适的初始聚类中心极易陷入局部最优，而且K-means算法难以准确判断出聚类数目是否合适。因此对传统算法进行优化与改进：首先，通过设定距离阈值选择初始聚类中心，并根据计算结果实现聚类数目的自动生成；然后，计算数据点同邻近点之间的距离，并与阈值进行比较，实现对K-means算法的聚类改进。改进的K-means算法可描述为：设D为数据集，n为其中包括的数据对象数量，λ为距离阈值，以此作为输入，D′为最终分为k组的聚类中心数据集，作为输出。具体操作流程如下[4]。

1)随机选择样本数据对象αi作为初始聚类中心C1，αi∈D，聚类中心数量初始值k=1；

2)for(αi∈D，i≠j)；

3)if(欧氏距离d(αi，Cn)>λ)；

4)k=k+1；

5)end if；

6)以Cn为中心完成d(αi，Cn)的计算，将αi划分到欧氏距离d(αi，Cn)最小的类中；

8)end for；

9)for(∀αi∈D)；

10)重复步骤6)、7)；

11)if(生成的Cn保持稳定)；

12)输出聚类中心数据集D′；

13)end if；

end for；

在入侵检测中，分别计算测试集中的各样本点β同改进算法中获取的各Cn(聚类中心)的欧氏距离，从中选取出p个距离最小的点，对其聚类中心的攻击类别进行判断，在类别数目相等的情况下将β划分到与它距离最近的点的聚类之中[5]。由此，在网络入侵攻击的训练数据集中，即可通过改进的K-means算法实现正常网络连接与网络入侵攻击的聚类划分。

3 入侵检测数据集与检测算法流程

3.1 NSL-KDD数据集

NSL-KDD数据集有效解决了KDDCPU99的数据冗余问题，将其作为网络入侵检测的数据集，其中包含的网络流量数据中各条网络连接数据均由1个类别标签和41个连接属性值构成。取NSL-KDD中125 973条网络连接记录作为训练集，22 544条网络连接记录作为测试集，其中测试集包括正常数据连接Normal类型以及DOS、Probe、U2R、R2L等39种攻击类型，训练集中包含22种攻击类型，以此进行算法训练。

3.2 多级混合式网络入侵检测算法流程

综合基于 PReLU激活函数的ELM算法和改进的K-means算法的优点构建多级混合式网络入侵检测算法流程，如图1所示。首先，由于DOS和Probe攻击会快速将大量连接请求发送至同一目标计算机，并且这两种网络入侵类型和正常的Normal网络连接数据有较大的差异性，因此采用基于PReLU激活函数的ELM算法在第一、二层先将DOS和Probe两类攻击区分出来。其次，由于U2R和R2L类攻击需获得目标计算机的非法访问权限，生成的网络连接记录与正常的Normal网络连接记录具有较高的相似性，攻击的数量相对较少，在区分完DOS和Probe两类攻击后，对剩余数据再采用改进的K-means算法进行聚类分析。

图1 多级混合式网络入侵检测算法流程

4 实验测试与结果分析

4.1 实验准备

为了验证设计的多级混合式入侵检测算法的实际检测效果，采用intel corei5 CPU、RAM计算机和MATLAB完成实验平台软硬件环境的搭建，基于NSL-KDD数据集进行仿真实验，具体实验参数定义见表1。

表1 实验参数定义

为评价算法的检测效果，基于表1的实验参数采用精确率、召回率、准确率、F1值、检测率、误报率6项指标进行综合分析与衡量，计算方式如下：

1)精确度，Precision=TP/(TP+FP)；

2)召回率，Recall=TP/(TP+FN)；

3)准确率，Accuracy=(TP+TN)/(TP+TN+FP+FN)；

4)F1值，F1-measure=2×precision×Recall/(precision+Recall)；

5)检测率，DetectionRate，指正确分类数据在总体测试集中的占比；

6)误报率，FalseAlarmRate=FP/(TP+FP)[6]。

4.2 数据预处理

分别从NSL-KDD的训练集与测试集中抽取10 000条数据验证算法的有效性，样本中网络连接的数据类别见表2。

表2 样本中网络连接的数据类别

首先，对数据进行预处理，将字符型特征转化到数值特征，根据标注的攻击类型将训练数据分为Normal、DOS、Probe、U2R、R2L共5类。

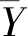
再次，对数据进行归一化处理。设Y1min和Y1max分别表示特征值标准化后的最小值和最大值，则进行归一化处理后得到特征值的归一值Y2为：

4.3 实验结果分析

将本文算法同BP神经网络、SVM和ELM算法进行比较实验，得到不同算法的检测率以及检测效果的对比结果见表3、表4。

表3 不同算法检测率比较 %

表4 不同算法检测效果比较 %

实验结果表明，与传统的BP神经网络、SVM和ELM算法相比，本文方法在正常的Normal类型以及各类攻击类型方面均表现出了较佳的检测效果，Normal类型检测率为99.38%，DOS类型检测率为98.98%，R2L类型检测率为99.08%，Probe类型和U2R类型由于样本数量较少，整体检测率偏低，但与传统算法相比仍有较大提升。在整体检测效果上，本文算法有效降低了检测的误报率，显著提高了检测准确率，足以证明本文算法在网络入侵检测方面行之有效[7]。

5 结束语

为了准确、高效地检测出网络正常数据和异常攻击，本文综合多种数据挖掘算法的优点完成了一种多级混合式入侵检测方法的设计，在传统ELM 算法中引入了PReLU 激活函数提升检测算法的分类效果，利用改进的K-means算法提高了聚类分析的准确性。通过NSL-KDD数据集进行的仿真实验结果表明，与BP神经网络、SVM、ELM算法等传统检测方法相比，本文方法检测率更高，且精确度高、误报率低，在网络入侵检测方面具有良好的实际应用效果。