基于量子遗传算法的回焊炉参数设定

陈恒宇，丁唯一，殷寰宇，沈世云

(重庆邮电大学 a.通信与信息工程学院；b.理学院， 重庆 400065)

随着电子信息产业的迅猛发展，表面贴装工艺(SMT)的质量和效率日益提高。传统的PCB加工工艺已经不能适应高质量、高效率的生产，越来越精密的元器件材料对原有的SMT技术提出了严峻的挑战。回流焊工艺是SMT生产线的核心环节，它通过改变温区的温度和传送带速度有效防止焊接缺陷或损坏等问题，提高了焊接质量，降低了生产成本。由于回焊炉种类和品牌、加热方式不同，需要对实际工程的回流焊炉温曲线进行测量，以便通过算法得到合适的回焊炉参数，优化和控制炉温曲线，从而提高产品质量和生产效率。解决这类问题需要分析回焊炉与焊接区域的热量交换过程，综合考虑各种传热方式和边界条件，建立回焊炉内的热传递模型。

目前，已有国内外学者对回流焊炉温曲线及回焊炉参数的优化进行了探讨。李楠等[1]通过进行回归分析和微分方程拟合炉温曲线，得出炉温曲线超过制程界限的时间，但未具体研究电路板通过回焊炉的过程。王明泉等[2]建立了一维偏微分方程热传导模型，通过有限差分求解炉温曲线。汤宗健等[3]通过实测数据，记录回流焊温度曲线，并基于回流焊炉炉温监控的炉温管控分析，计算回焊炉的制程能力，得出在获取可靠的炉温曲线后，只需要加强炉温监控即可保证焊接质量的结论。席晨馨[4]通过微分方程模型和模拟退火算法，以阴影面积为目标函数，得到最优炉温曲线。宋会良[5]通过研究在SMT制造工艺中影响回流焊接质量的主要因素，得出比较贴切的参数值，并针对性地提出工艺方法改善方向。

本文基于现有研究，从回流焊过程的实际情况出发，建立非稳态热传递偏微分方程模型与炉温曲线模型，同时考虑各类约束条件，以炉温曲线的覆盖面积和对称性为目标函数，建立炉温曲线参数优化模型，基于量子遗传算法对模型进行求解，并研究不同算法的求解效率及对结果的影响。

1 炉温曲线优化模型

回焊炉系统的基本组成如图1所示，它由预热区、恒温区、回流区和冷却区4大温区组成，每个温区中又包含数量不同的长度为30.5 cm、间隙距离为5 cm的小温区，电路板两侧搭在传送带上均匀进入炉内进行加热焊接。

在建立坐标系之前，首先需要判断焊接区域在厚度上是否有显著的温度变化。毕渥数Bi表征固体内部热阻与外部热阻的比值，当其显著小于1时，可以说明固体内部的温度梯度很小，可以忽略内部温度的变化。对于厚度为d，传热系数为H，两侧受热时导热系数为λ的均匀电路板，其毕渥数Bi的计算公式为[6]：

(1)

本文讨论的电路板焊接区域厚度d=0.15 mm，典型的对流回流过程中的平均传热系数H=50 W/m2，因此毕渥数的大小仅取决于导热系数λ。通过查阅文献[7]，电路板通常由铜箔、FR4和BGA这3种材料组成，各材料的导热系数λ见表1。

表1 铜箔、FR4和BGA材料的导热系数

当材料为FR4时，导热系数最小，对应求得的毕渥数最大，Bi=0.012 9<<1。这说明在焊接区域厚度方向基本不存在温度梯度，因此对焊接区域建立热传递模型时可以忽略厚度的影响，只需考虑回焊炉在传送带运动方向的温度变化，建立一维热传递模型和如图1所示坐标系。图中，蓝色方块表示小温区，紫色小矩形表示温区之间的间隙，坐标原点对应着回焊炉炉前区域的起点，x轴正方向为传送带的速度方向。

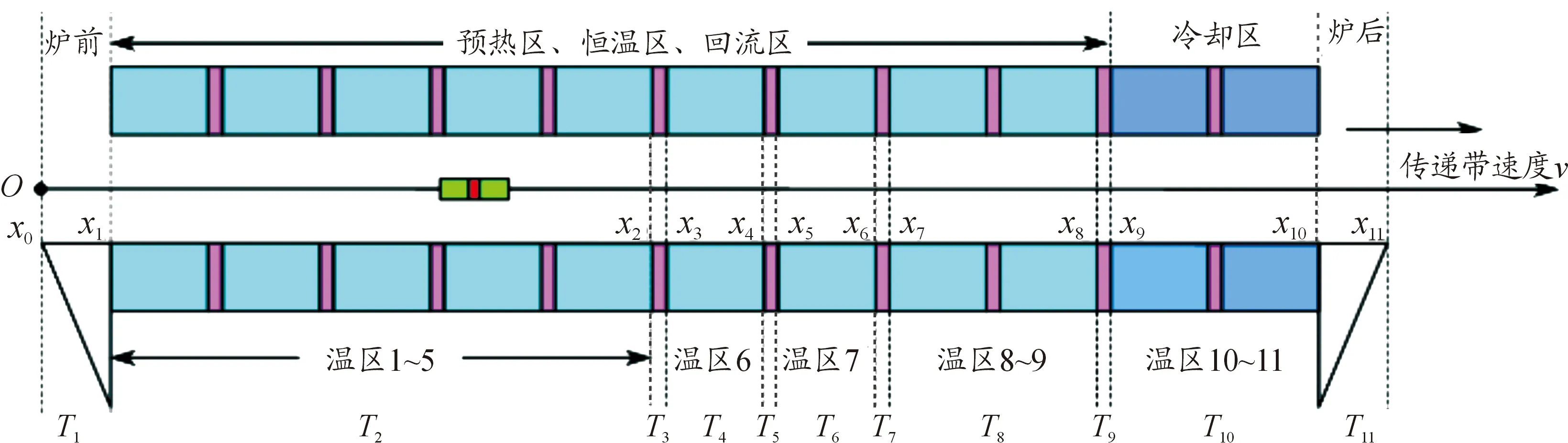
图1 回焊炉系统构成

在实际生产过程中，可以通过调节各温区的设定温度以及传送带的过炉速度，即回焊炉的工艺参数来控制产品质量，调节过程中，小温区1～5、8～9的温度分别保持一致，小温区10～11保持25 ℃。

由温度传感器测出的电路板焊接区域中心的实时温度曲线称为炉温曲线，在回焊炉电路板焊接过程中，炉温曲线需要满足表2所示的制程界限，各温区与传送带速度也需要满足表3中的调节范围。

表2 制程界限

表3 调节范围

在建立模型的过程中，本文假设温度传感器测量位置为焊接区域表面中心，忽略了测温区域的宽度与厚度，且认为温度相同的小温区之间间隙温度与相邻温区相同。基于上述假设以及热传递方程[8-9]，可以建立回焊炉内的热传递模型。

1.1 非稳态热传递模型

回焊炉启动后，炉内空气温度经过一段时间达到稳定，之后方可进行焊接工作。在稳定前，由于各温区温度设置不同，炉内冷热空气之间会发生热量交换。因此，需要对炉内空气的传热方式进行机理分析，建立一维非稳态传热模型，对稳定时回焊炉的温度分布进行求解。

对于炉前区域(区域1)和相邻温区温度不同的间隙(区域3、5、7、9)，在整个区域内温度达到稳定之前，空气之间的热量交换形式为热传导，由此可以得到各区域中热传导的偏微分控制方程：

(2)

其中，Ti表示图1中第i个温区的温度，c、ρ和λ分别表示炉内空气的比热容、密度和导热系数，其取值如表4所示。

表4 空气比热容、密度和导热系数的取值

回焊炉刚启动时为零时刻(t=0)，假设此时区域1、3、5、7、9内空气的温度与其左侧相邻区域中的温度相同，可以得到各区域热传递方程的初始条件：

(3)

在回焊炉内各区域的交界处，空气会与炉壁之间发生对流传热，吸收或释放热量，且该过程符合牛顿冷却定律。对于炉前区域来说，其左边界与回焊炉壁(25 ℃)发生热对流，右边界与温区1(175 ℃)发生热对流，因此可以得到炉前区域的边界条件：

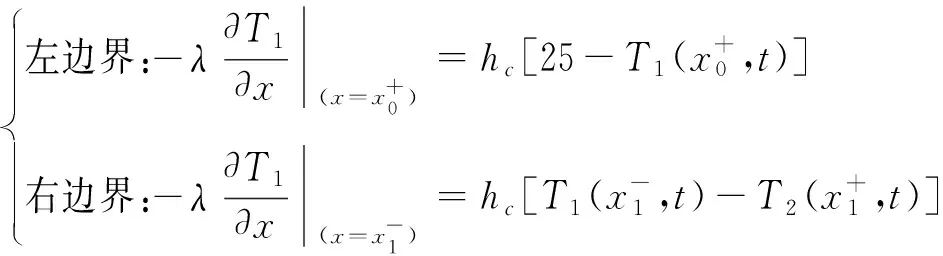
(4)

其中，hc为炉内空气的对流交换系数，其取值范围通常为1～10 W/m2·℃[10]，本文在计算时取hc=8。

对于区域3、5、7、9来说，其左边界与左侧相邻小温区的炉壁发生热对流，右边界与右侧相邻小温区的炉壁发生热对流，因此采用同样的计算公式可以得到间隙的边界条件：

i=3，5，7，9

(5)

1.2 炉温曲线模型

电路板在小温区中主要通过热对流和热辐射的方式获得热量，为了简化模型，参照文献[11]将辐射传热转化为对流传热进行计算。当焊接区域处于第i个小温区内，其温度变化方程为

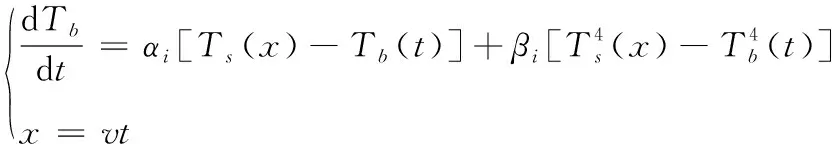
(6)

其中，i=1，2，…，11，Tb(t)表示t时刻焊接区域中心的温度；x为焊接区域中心的坐标，Ts(x)表示x处回焊炉的温度；αi和表示第i个小温区内与热对流和热辐射相关的系数。

当电路板处于炉前区域、第i个与第i+1个小温区之间的间隙或炉后区域时，受到热对流的影响，其温度变化方程为

(7)

式中，γ0和γ11分别表示炉前和炉后区域内与热对流相关的系数；γi(i=1，2，…，10)表示第i个与第i+1个小温区之间间隙内与热对流相关的系数。

1.3 炉温曲线优化模型

理想的炉温曲线应使超过217 ℃到峰值温度所覆盖的面积最小，且以峰值温度为中心线的两侧超过217 ℃的炉温曲线尽量对称，因此需要通过调整回焊炉各温区的设定温度和传送带的过炉速度，对炉温曲线进行优化。

对于覆盖面积S，可以通过积分求得

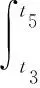
(8)

对于对称程度f，本文将峰值两侧超过217 ℃对称位置的平均温度之差作为其衡量指标，f越小表示每对位置的平均温度之差越小，炉温曲线的对称程度越高。即

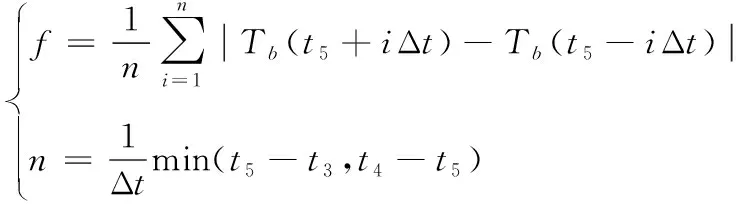
(9)

式(9)中，t3和t4分别表示焊接区域中心温度上升和下降过程中最接近且大于217 ℃的对应时刻；t5为炉温曲线峰值对应的时刻。

由于焊接区域中心温度的变化为时间t的隐函数，所以只能使用数值积分的方法求出面积的近似值，当采用梯形公式进行计算时，覆盖面积可表示为

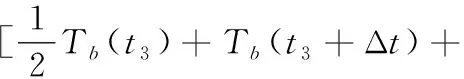
Tb(t3+2Δt)+…+Tb(t3+nΔt)+

(10)

调整回焊炉系统参数可以改变炉温曲线，进而影响覆盖面积和对称程度，所以S与f是系统参数的函数，即

(11)

因此，优化模型的目标为

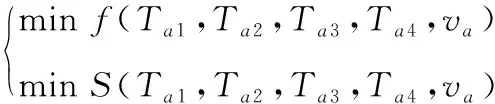
(12)

如果将双目标优化转化为2个单目标优化模型并求解，发现2种情况下的最优解之间有着较大的差距，导致2个目标无法同时达到最优，需要综合考虑模型的2个优化目标，具体的改进方法为：假设在炉温曲线优化的过程中，应当优先满足对称程度最高的要求，覆盖面积只需要满足小于上界值St即可，由此可以将覆盖面积最小的优化目标转化为一个约束条件，实际操作时只需要根据工程要求调整上界值即可。

工艺窗口指数PWI是由KIC提出的一个能快速判断温度曲线合格性的工具。在一条温度曲线中，全部制程界限对应的参数都能各自生成一个PWI值，用来表示实际曲线参数与理想参数之间的偏移程度，参数的PWI中最大的用来表征曲线的PWI值，即

(13)

其中，n=5表示炉温曲线制程界限的5种类型，mi为当前炉温曲线对应的第i个制程界限参数的值，ai和ri分别为第i个参数上下限的平均值与区间长度，其取值参照表2。PWI≤100表示炉温曲线符合工艺规格。

综合考虑覆盖面积与对称程度2个优化目标，以及工艺窗口指数和系统参数调节范围，可以建立如下优化模型：

(14)

2 回焊炉热传递模型的求解

2.1 回焊炉内的温度分布

本文采用有限差分法将1.1中的偏微分方程转化为差分方程的形式，对回焊炉内的温度分布进行求解。首先将方程进行如图2所示的离散化处理。

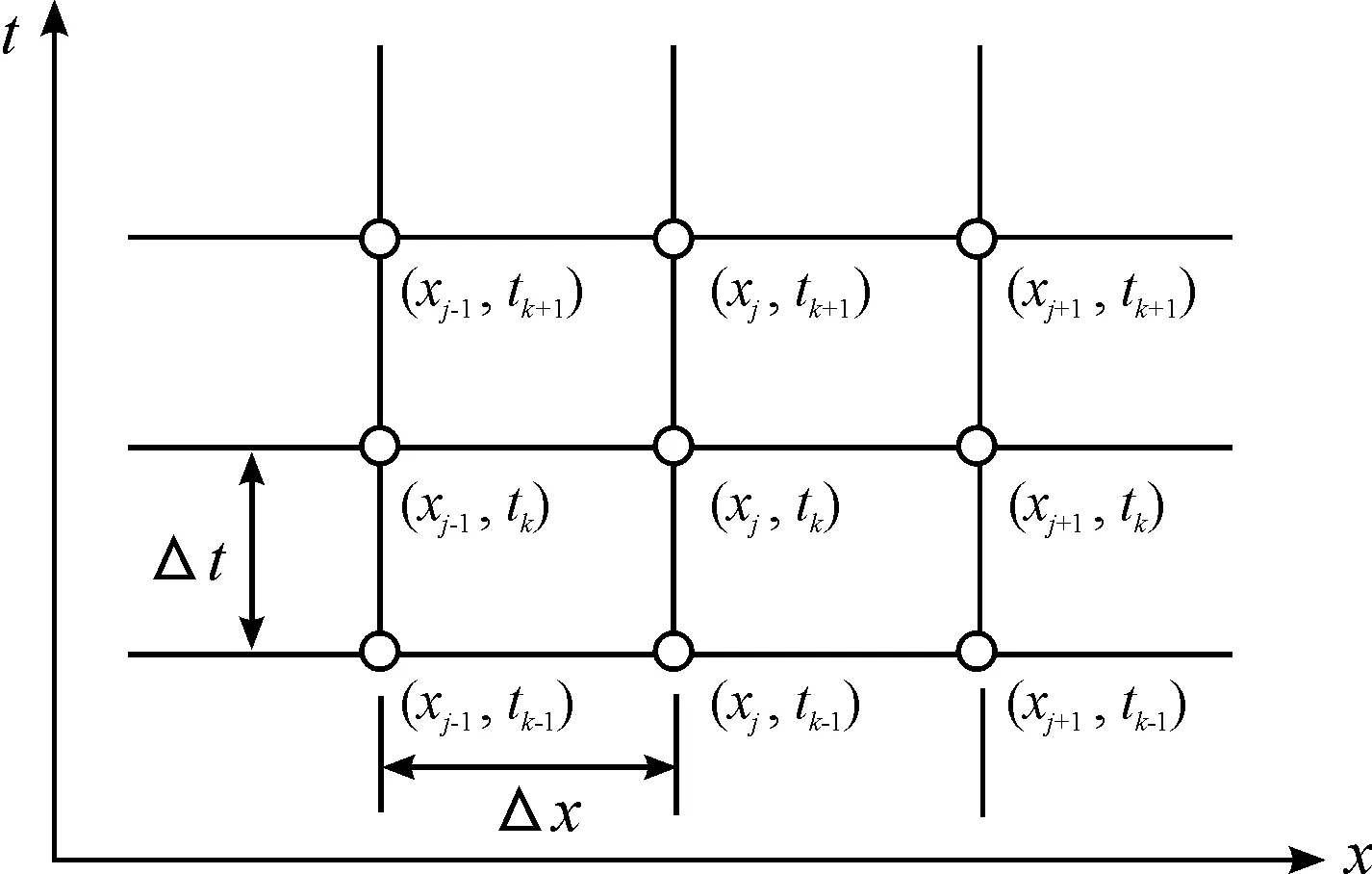
图2 有限差分法的网格划分

网格中的每个结点都为差分方程中的一个离散点，Δx=0.2 cm和Δt=0.05 s分别表示位置x方向和时间t方向的步长，j和k分别表示离散点在x轴和t轴上的坐标。用(j，k)简化(xj，tk)，则Ti(j，k)=Ti(xj，tk)。将一阶偏导用一阶向后差商近似，二阶偏导用二阶中心差商近似，可将式(2)转化为

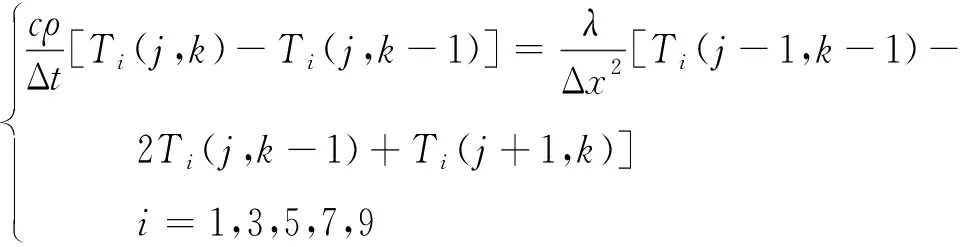
(15)

设各区域分界线坐标xi(i=0，1，…，11)在有限差分过程中对应的j的取值为mi(i=0，1，…，11)。对于炉前区域与区域3、5、7、9，左边界的边界条件的一阶偏导用一阶向前差商近似，右边界的边界条件的一阶偏导用一阶向后差商近似，得到边界条件的差分方程组

(16)

其中，i=1，3，5，7，9，T0=25 ℃。

以时间间隔Δt为步长不断迭代，得到每个时间层上回焊炉内不同位置空气的温度分布情况，所得结果如图3所示。从图3中可以看出：随着时间的增加，炉内各处温度最终稳定，为了便于观察稳态时各位置处的温度，做出温度稳定后各位置处的温度情况，如图4所示。

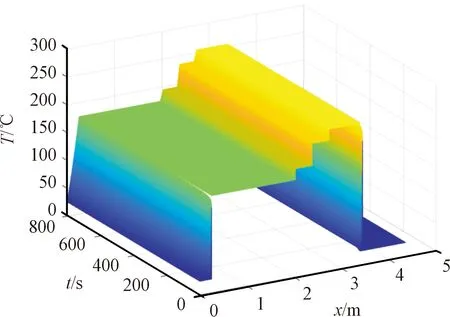
图3 回焊炉内温度变化图

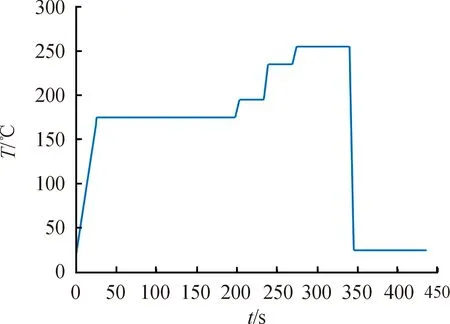
图4 回焊炉稳定后的温度分布曲线

2.2 炉温曲线模型的求解

同样采用有限差分法将式(6)和(7)转化为如下差分形式

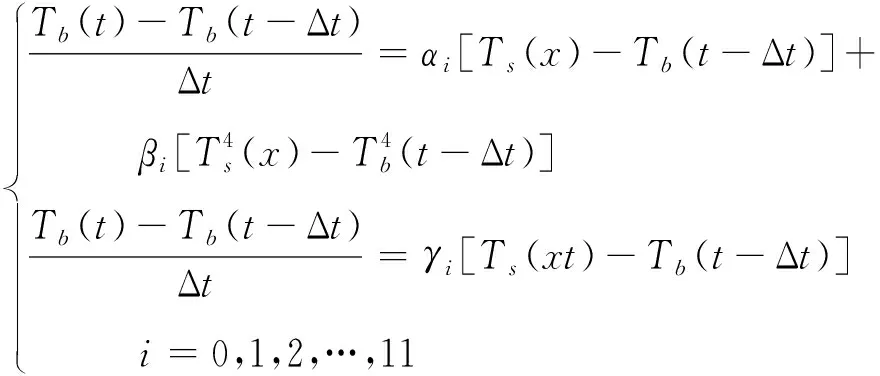
(17)

以时间间隔Δt为步长依次迭代计算，可以得到焊接区域中心温度随着时间的变化情况。由于方程中的αi、βi和γi均未知，所以需要根据测量的真实值进行曲线拟合。将拟合出的各系数代入炉温曲线模型中计算，得到计算出的炉温曲线。计算值与实测值的总残差平方和为2 244.053 5，平均误差为1.401 2 ℃，拟合效果较好。此时，计算出的炉温曲线与实测曲线如图5所示。

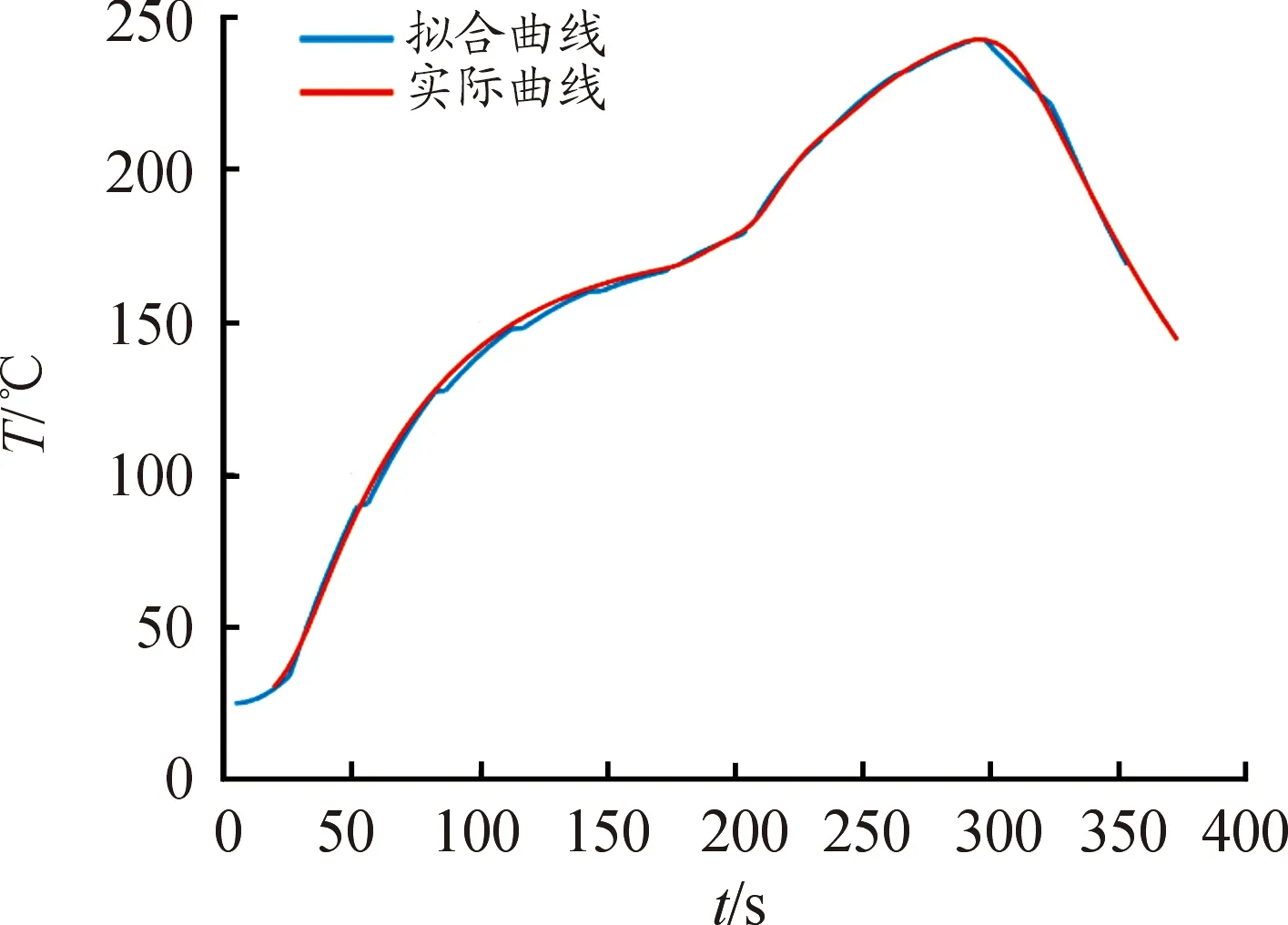
图5 拟合的炉温曲线与实测炉温曲线

3 基于量子遗传算法求解回焊炉最优工艺参数

量子遗传算法是量子计算与遗传算法相结合的概率优化算法，由于量子态具有叠加、纠缠和干涉等特性，使用量子比特进行染色体编码与量子逻辑门更新染色体比传统算法具有更高的并行性与更广泛的搜索空间[12]。本文1.3中建立的炉温曲线优化模型是一个NP问题，且由于变量较多，解空间较大等原因对算法的要求较高，因此采用量子遗传算法实现目标的优化求解。

3.1 算法的实现

1) 染色体的编码

量子遗传算法使用量子比特表示染色体编码，一个量子比特同时处于若干个幅度之和为1的量子态的叠加态中，比如

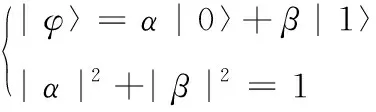
(18)

优化模型中共有5个参数，因此采用多量子比特编码后第k代的第i个基因Qj(k)可以表示如下

2) 量子旋转门

采用量子旋转门更新染色体的具体操作如下，其中θi表示旋转角，其取值由调整策略确定。

(19)

3) 算法的整体实现

在遗传算法中，个体的适应度由优化目标决定，即适应度函数为以回焊炉参数为因变量，炉温曲线对称程度为自变量的非线性函数；遗传算法对各参数进行编码与更新，并在适应度函数中加入优化模型的约束条件作为筛选的条件。算法的设计流程如下所示：

1) 设置最大遗传代数为250，覆盖面积上限为400，初始化个体数为50的种群Q(t0)，随机生成以20个量子比特为编码的染色体；

2) 测量初始化种群Q(t0)中的每个个体，得到确定解P(t0)的二进制编码；

3) 将确定解P(t0)代入炉温曲线模型，得到曲线优化区域的对称程度，并将其作为该解的适应度；

4) 记录种群中最优个体对应的适应度；

5) 以最优个体适应度小于0.9且连续50代保持不变为结束条件，判断算法是否结束，若未满足结束条件则继续计算；

6) 测量种群Q(t)中的每个个体，得到确定解P(t)的二进制编码；

7) 将确定解P(t)代入炉温曲线模型，得到曲线优化区域的对称程度，并将其作为该解的适应度；

8) 利用量子旋转门U(t)对个体实施调整，得到新的种群Q(t+1)；

9) 记录最优个体对应的适应度，t=t+1，返回步骤5；

算法的整体实现流程如图6所示。

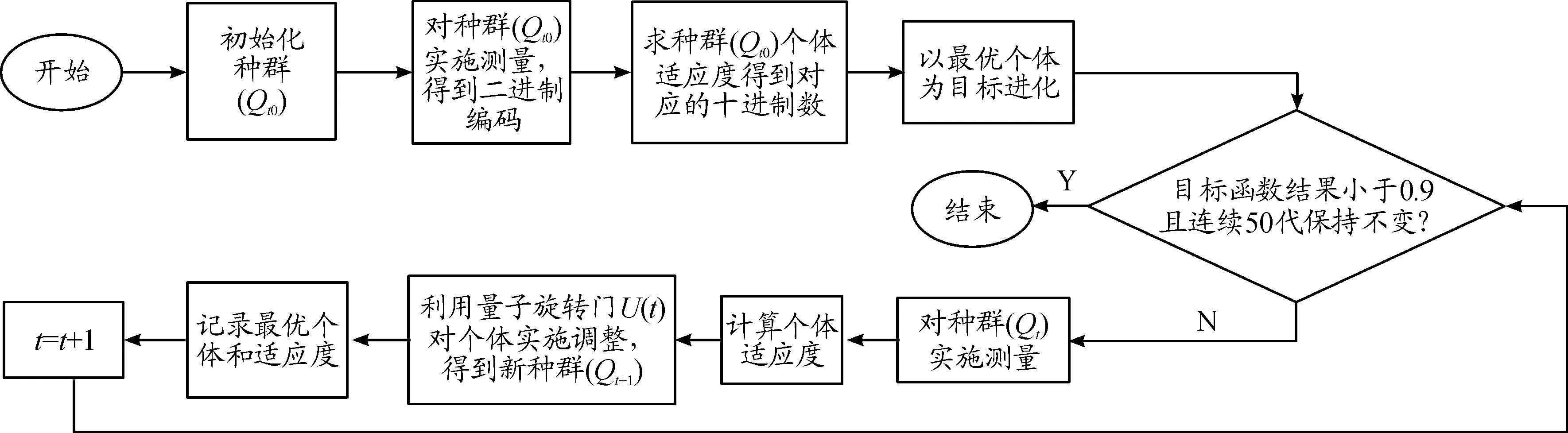
图6 量子遗传算法实现流程框图

3.2 结果分析

根据1.3中建立的炉温曲线优化模型与上文所述量子遗传算法，运用Matlab编写代码求解，得到的结果如表5所示，对应的适应度为0.732 4。

表5 空气比热容、密度和导热系数

为了验证算法的高效性，本文将量子遗传算法与遗传算法和改进的模拟退火算法进行比较。设定遗传算法和量子遗传算法种群大小为50，迭代次数为250代，改进的模拟退火算法先在解空间中定步长遍历搜索，再将最优解作为初始解，迭代次数同样为250代。图7为3种算法的求解结果，其中横坐标表示迭代次数，纵坐标表示目标函数值。表6为不同迭代次数下3种算法求得的最优目标函数值。

根据表6与图7，在迭代开始时，量子遗传算法迭代曲线斜率的绝对值大于其他2种算法，在30代左右求得最优解并收敛，遗传算法在50代收敛，模拟退火算法在160代收敛，量子遗传算法收敛速度快于普通的遗传算法和模拟退火算法；在迭代结束时，遗传算法和模拟退火算法求得结果相差不大，量子遗传算法求得的目标函数值也明显小于其他2种算法。

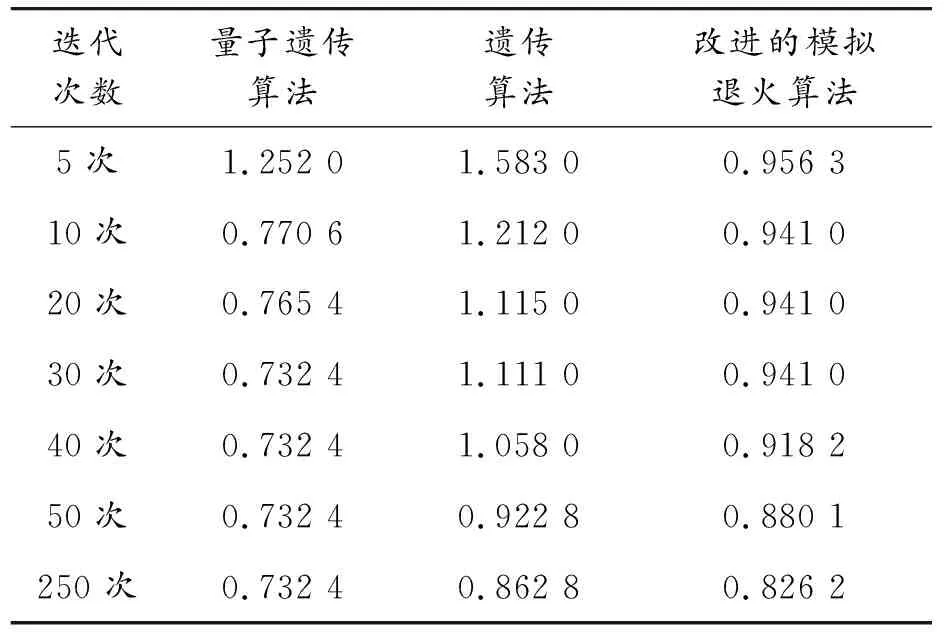
表6 迭代次数不同时3种算法的求解结果

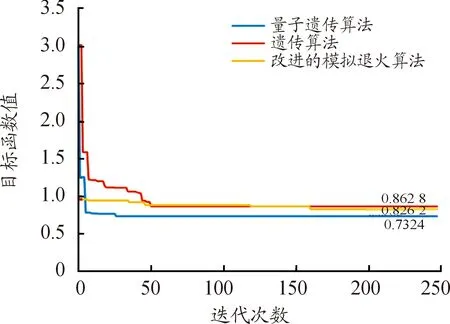
图7 各算法的性能对比

上述结果表明：求解本文建立的优化模型，采用量子遗传算法比普通遗传算法和改进的模拟退火算法具有更高的效率，且求得的结果更优。

4 结论

本文对回流焊曲线参数优化问题进行了研究，基于量子遗传算法对回焊炉参数设定问题进行求解。该算法改进了染色体的编码方式，用量子比特表达一个基因使得该基因处于“0”态、“1”态或者任意叠加态，包含所有可能信息，优化了传统遗传算法基因只能表达某一确定信息的缺点。在相同条件下求解最优炉温曲线参数，量子遗传算法比遗传算法和改进模拟退火算法迭代次数更少，求解结果更优，因此可以进一步提升产品质量，提高生产效率，从而满足当前电子产品更新迭代快、竞争激烈的需求，增强企业核心竞争力。后续的研究将继续优化算法，进一步提高算法的效率，实现产品质量的提升与生产成本的降低，实现经济效益与社会效益的显著提升。