无人机伺服云台控制方法研究
2021-10-19刘家伦
刘家伦
(北京精密机电控制设备研究所 航天伺服驱动与传动技术实验室, 北京 100076)
1 研究现状
无人机机载云台是无人机载荷的运动控制单元,其设计目标为通过多个伺服电机的协同控制,实现无人机运动、姿态变化及自身振动的环境下机载载荷姿态相对于惯性坐标系的角度稳定及可控,从而保持载荷图像稳定。载荷中心为监控目标。无人机云台姿态控制的反馈源主要包括陀螺仪、编码器以及载荷视觉处理器等。目前,基于视觉反馈的云台控制方式已经非常常见,闫磊等[1-9]介绍了多种基于视觉反馈的伺服云台控制方法,均着重阐述了视觉处理相关的内容。关旭宁等[10-15]则从控制算法的角度着重研究各种控制算法在伺服云台上的应用及其效果,包括补偿控制[10]、自适应跟踪控制[11]、基于布谷鸟搜索的云台控制[12]、模糊自整定PID控制[11]、LQR控制[13]、双速率换串级控制[14-15]等控制算法在伺服云台上的应用。周辉[16]从云台控制系统架构设计的角度阐述了稳像云台的原理、模型及控制方法,程杰等[17]及刘欣等[18]则从体感云台或手持云台的研究角度研究了在该种工况下的控制方式及方法。
目前,虽然研究云台控制方法的已有文献较多,但大多从视觉图像处理或控制算法方向出发,未从无人机伺服云台多模式控制的角度进行分析,且没有综合无人机机载云台自稳、跟踪状态下的扰动力矩的模型情况。为此,从实际工程应用出发,对无人机机载伺服云台控制系统的多模式控制方法及分析方法进行研究及仿真。无人机载荷伺服云台通常为2轴或3轴控制,可对俯仰角、偏航角及横滚角进行调节,并且3个轴方向的载荷姿态调节可分别通过各自对应的伺服电机进行解耦控制,故主要基于云台的单轴多模式控制进行分析,另外两轴的控制方法类似。
机载云台主要有3种控制模式,即手动模式、自稳模式和跟踪模式。3种控制模式的功能如下:
1) 手动模式:控制人员手动调节云台的俯仰方向以及偏航方向。
2) 自稳模式:云台控制器根据无人机的姿态变化,克服无人机姿态变化以及电机自身齿槽转矩带来的摩擦力矩或扰动力矩,自动调节云台相对无人机的俯仰姿态与横滚姿态,继而保持云台相对惯性系的俯仰姿态和横滚姿态不变。
3) 跟踪模式:云台控制器得到了基于图像的目标脱靶量数据后,计算出云台当前姿态相对指向目标时姿态的偏差,通过控制器控制伺服电机消除姿态偏差,之后进入自稳状态或持续根据跟踪目标在图像中的目标位置,确保跟踪目标持续在图像中点附近。
对以上3种控制模式的实现方式进行设计,并基于伺服电机的数学模型以及3种模式的控制原理,对控制算法的执行效果进行仿真研究。
2 伺服电机选型与数学模型
2.1 伺服电机选型
电机是云台稳定系统的关键部件。由于本文中云台稳定系统工作在低速状态下,所以电机必须具备转速低、响应快、力矩大、功耗小、线性度好等性能。直流力矩电机非常适合这种工作要求,其控制方式与普通直流无刷电机类似,驱动电路为三相逆变桥,通过控制三相绕组的相电压变换,实现电机驱动。
伺服云台控制目标设计为小型枪械载荷,控制精度目标为1毫弧度,根据挂载载荷数据,载荷形状按照近似圆柱体计算整个枪体的转动惯量,其中m枪=2.65 kg,枪长l枪=0.726 m,圆柱体平均半径小于0.05 m,故可近似计算出载荷转动惯量约为J=0.116 kg·m2。根据载荷形状特性,可近似认为俯仰及偏航方向转动惯量一致。
为使云台具有较高的性能,设计云台角速度在0.1 s左右能够从静止加速到1 rad/s。因此,最大角加速度值为αmax=10 rad/s2。考虑飞行时的风场、力矩电机齿槽转矩等因素,干扰力矩按照Md= 0.1 N·m,则M-Md=J*αmax=1.16 N·m,则Mmax>1.26 N·m。
根据输出扭矩的参数需求,选择Allied Motion 公司MF系列MF0095020型直流力矩电机,其额定输入电压为48 V,额定扭矩为1.73 N·m,在满足需求的前提下基本仍有部分冗余。具体参数见表1。

表1 MF0095020型直流力矩电机参数
2.2 伺服电机的数学模型
直流力矩电机的单相绕组可近似认为是电感与电阻的串联,直流力矩电机单相绕组的等效电路见图1。
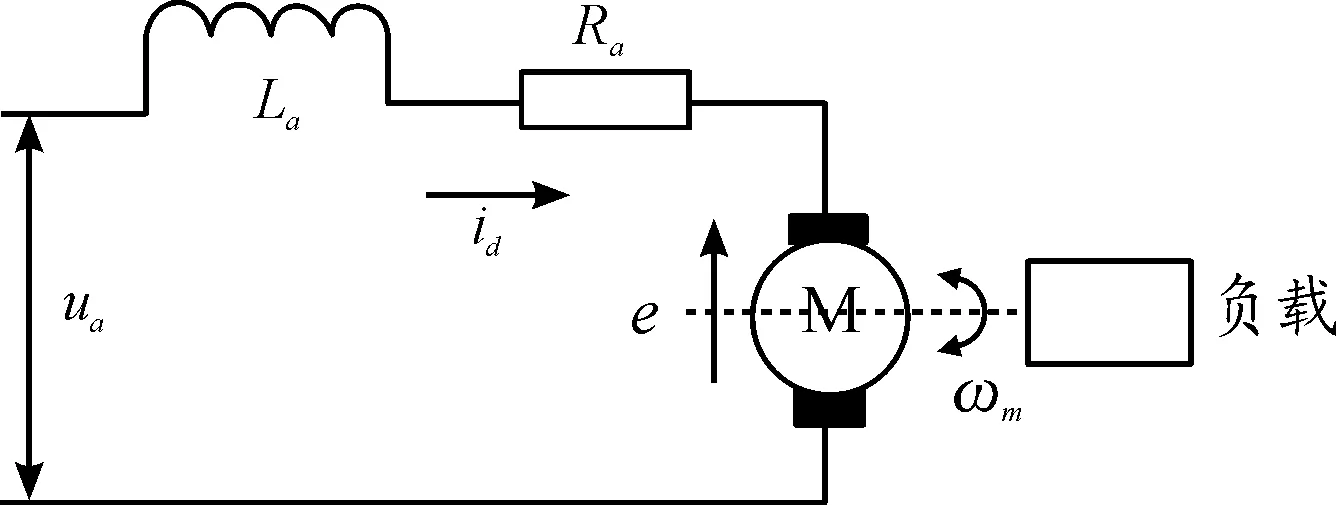
图1 驱动电机等效电路示意图

根据电路回路原理可知:
(1)
式(1)的拉氏变换形式为:
(2)
由ia产生的电机输出扭矩为:
(3)
其中反电势是由电机旋转引起的:
e(s)=keωm(s)
(4)
由动量矩得平台负载传递函数为:
(5)
综合式(5)得:
(6)
可得平台负载及力矩电机数学模型为:

图2 力矩电机数学模型
在干扰力矩Md=0时,电机的传递函数为[8]:
(7)
3 手动模式
手动模式的功能是使控制人员直观地通过摇杆或按键持续控制云台以一定相对无人机的角速度转动,从而改变云台相对于无人机的俯仰角与横滚角。控制者通过载荷回传的图像数据决定何时停止改变云台相对于无人机的俯仰角与横滚角。在停止手动模式控制后,云台基于当前的陀螺仪姿态角反馈,进入自稳模式。
采用的电机驱动器为以色列Elmo Gold Twitter系列驱动器,在各个模式下均使用驱动器的电流环模式,在云台控制器软件中设计速度环和位置环控制。在电流环控制下,该控制器支持模拟量输入。由于在手动模式下,云台控制精度要求较低,无人机抖动对控制效果影响较小,故忽略无人机抖动对伺服云台产生的影响。手动模式控制示意图见图3。

图3 手动模式控制示意图
图3中,控制人员输入角速度后与编码器反馈的相对于机体坐标系的角速度做差后进入速度环控制器,经控制器计算输出模拟量进入驱动器,后驱动伺服电机按照指定方式转动。
根据控制人员习惯,设定在时间t=1 s时输入信号由0变为0.5 rad/s,在5 s时输入信号由0.5 rad/s变为0。基于图3的Simulink仿真系统如图4所示。图4中,阶跃信号与反馈信号的差值进入速度环PID控制器,经过限幅环节后输出代表绕组实际电压的模拟量,输入电压与反电动势做差后的电压进入如图2所示的电机模型中。仿真效果如图5所示。由图5可看出,手动模式下,速度信号能够得到快速响应[19],速度环控制器算法为常见PID控制。

图4 手动模式控制仿真系统示意图

图5 手动模式仿真效果图
4 自稳模式
在自稳模式下,云台控制器根据无人机的姿态变化自动调节云台相对无人机的俯仰姿态与横滚姿态,继而保持云台相对惯性系的俯仰姿态和横滚姿态保持不变。自稳模式中的角度反馈元件为陀螺仪。自稳模式下云台的单轴姿态控制回路如图6所示。
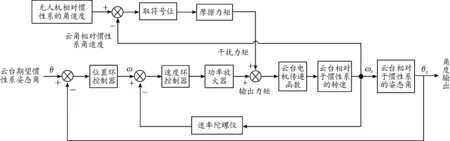
图6 自稳模式下的单轴姿态控制回路框图
如图6,在自稳模式下,云台控制系统的输入量为云台相对于惯性系的期望姿态角θ,θ与θ0做差后的差值进入位置环控制器。位置环控制器输出云台相对于惯性系的期望角速度指令ω,期望角速度指令ω与速度陀螺仪反馈的实际相对惯性系角速度ω0做差后进入速度环控制器。速度环控制器输出控制指令后通过功率放大器即驱动器后驱动伺服电机输出力矩值。
无人机相对于惯性系可能会有一定的角速度,且无人机机体相对于云台载荷可能会存在摩擦力矩或齿槽转矩。因此,当无人机相对于惯性系有角速度,且与云台载荷相对于惯性系速度不相等时,无人机本体相对于云台载荷必然会有摩擦力矩出现。此时,如果无人机机体相对于惯性系角速度大于云台载荷相对于惯性系的角速度,则该力矩为正向助力力矩,符号位为正,云台载荷上承受的力矩为伺服电机力矩加上摩擦力矩绝对值。反之,如果无人机机体相对于惯性系的角速度小于云台相对于惯性系的角速度,则该力矩为反向阻力力矩,符号位为负,云台载荷上承受的力矩为伺服电机力矩减去摩擦力矩绝对值。从图6中可以看出,云台载荷相对于惯性系承受的力矩为伺服电机力矩与摩擦力矩综合作用的结果,摩擦力矩为助力力矩还是阻力力矩则取决于无人机机体与云台载荷相对于惯性系角速度的差值。
伺服电机输出力矩与摩擦力矩叠加后施加在云台载荷上驱动云台输出角速度、角位置,再通过陀螺仪反馈角速度以及计算角位置,实现速度环、位置环闭环控制。
根据无人机测试数据,无人机在飞行时会产生一定的姿态抖动,经过减震器减震后传递到云台负载上的最大幅度为-0.2°~0.2°,最快频率约为10 Hz,故可近似认为无人机传递到云台载荷上的姿态角度抖动信号为幅值0.2°,频率10 Hz的正弦信号。当云台工作在自稳模式时,其姿态角输入θ=0,根据表1,可得τe=La/Ra=0.21/0.25=0.84,km=0.14 N·m/A,Ra=0.2 Ω,ke=0.14 V/rad/s。根据计算,载荷转动惯量约为J=0.116 kg·m2。根据表1,所选电机齿槽转矩约0.046 N·m,估算外部轴承、摩擦力矩约为0.05 N·m,则伺服电机在保持相对惯性系自稳需要克服的转矩可近似为0.1 N·m。
基于图6的控制回路框图,将上述仿真参数代入仿真模型中。各控制器使用PID算法,可得Simulink仿真程序如图7上半部分:无人机本体角位置信号Sine Wave1为正弦,微分后得到角速度,与云台角速度做差后取符号位,与摩擦力矩相乘后,叠加到输出伺服电机输出力矩中作为扰动力矩出现。云台角位置控制信号为阶跃信号Step(自稳模式控制状态下恒定为0°),经过位置环PID控制器、速度环PID控制进入电机控制模型,后输出角速度,并经过积分后得到角位置输入到Workspace4中,并反馈到位置环控制器中。
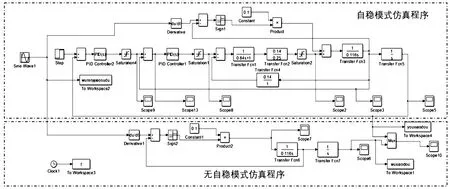
图7 自稳模式以及无自稳模式控制下的单轴姿态仿真程序示意图
为便于对比,同样对云台载荷在无自稳控制模式下的角位置情况进行仿真。在此状态下,云台载荷只受由无人机机体抖动及姿态变化带来的干扰力矩的作用。该部分仿真程序见图7下半部分:无人机角位置经过为分后得到其角速度,与现有云台现有角速度做差后取符号位,后与摩擦力矩结合后作用到云台载荷本体,其摩擦力矩即为云台唯一的驱动力矩。经过力学模型得到角速度,积分得到角位置,输出到Workspace1中与有自稳模式控制下的云台载荷角度进行比较。
图7中,设置各控制器的PID参数,并根据电机的物理特性增加限幅单元。电机力矩输出限幅为正负3.5 N·m,速度环输出限幅为正负48 V,阶跃输入信号幅值始终为0,无人机抖动信号θ机=0.003 5*sin(10*2*π)。加入取符号位环节控制表示扰动力矩方向为助力力矩或阻力力矩。
图8为无人机姿态角输出与云台姿态角输出曲线,图9为自稳模式的云台姿态角输出与无自稳控制时云台姿态角输出曲线,可知在自稳模式的控制下,不但可以有效减少云台的抖动幅度,也可防止云台姿态角漂移。

图8 无人机姿态角输出与云台姿态角输出曲线
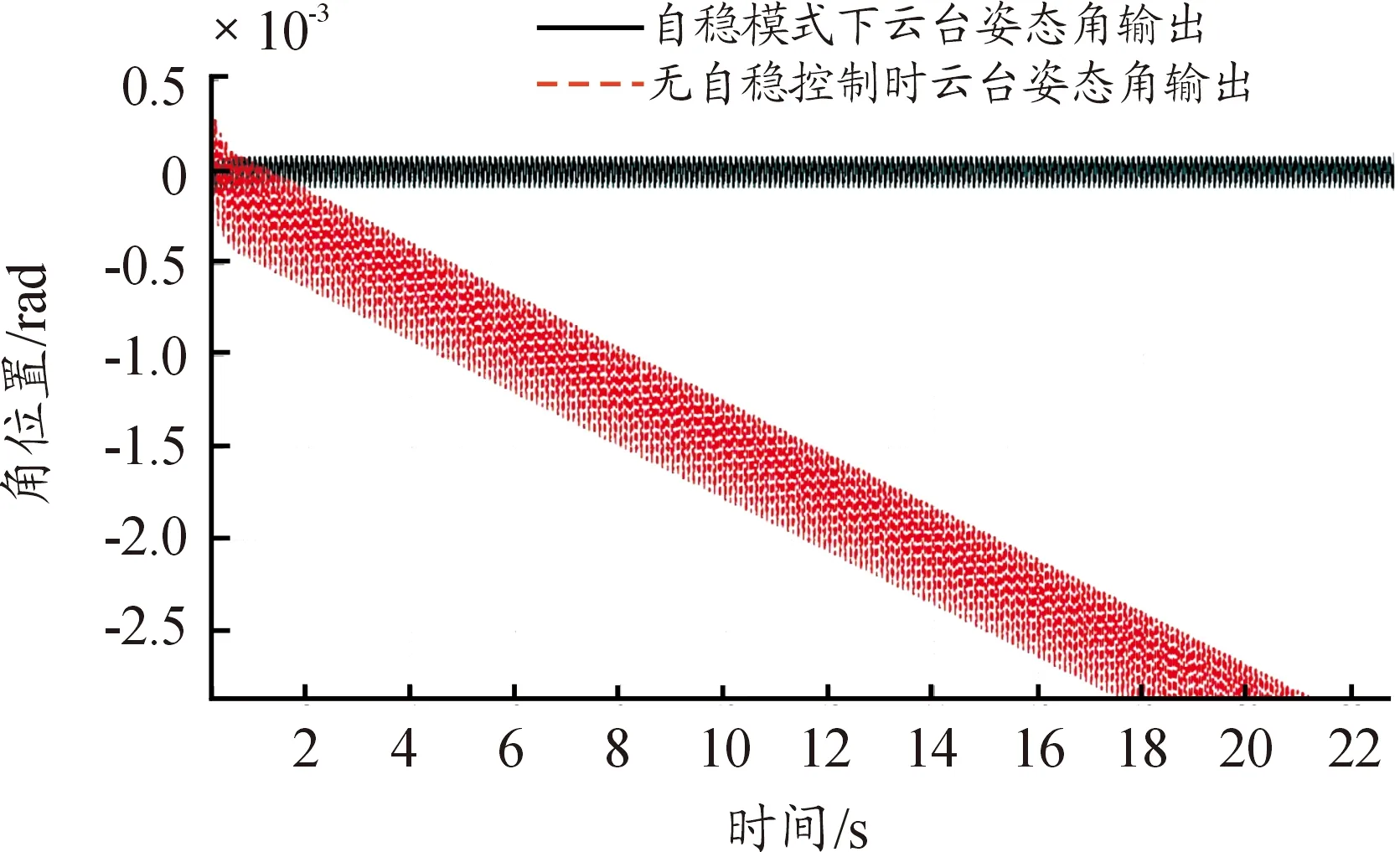
图9 自稳模式下云台姿态角与无自稳控制时云台姿态角输出曲线
为了验证控制算法在有幅值较高、频率较低的外部扰动时,伺服云台的控制情况,令无人机姿态角信号θ机=0.5*sin(0.5*2*π),即无人机的姿态角变化幅度为0.5 rad,频率为0.5 Hz。对在自稳模式下云台姿态角与无自稳控制时云台姿态角输出进行仿真,高幅低频干扰信号下的云台姿态角输出见图10。如图10所示,在有幅值较高、频率较低的外部扰动时,自稳模式同样能有效保证云台载荷的相对于惯性系的姿态角稳定在期望姿态角附近。
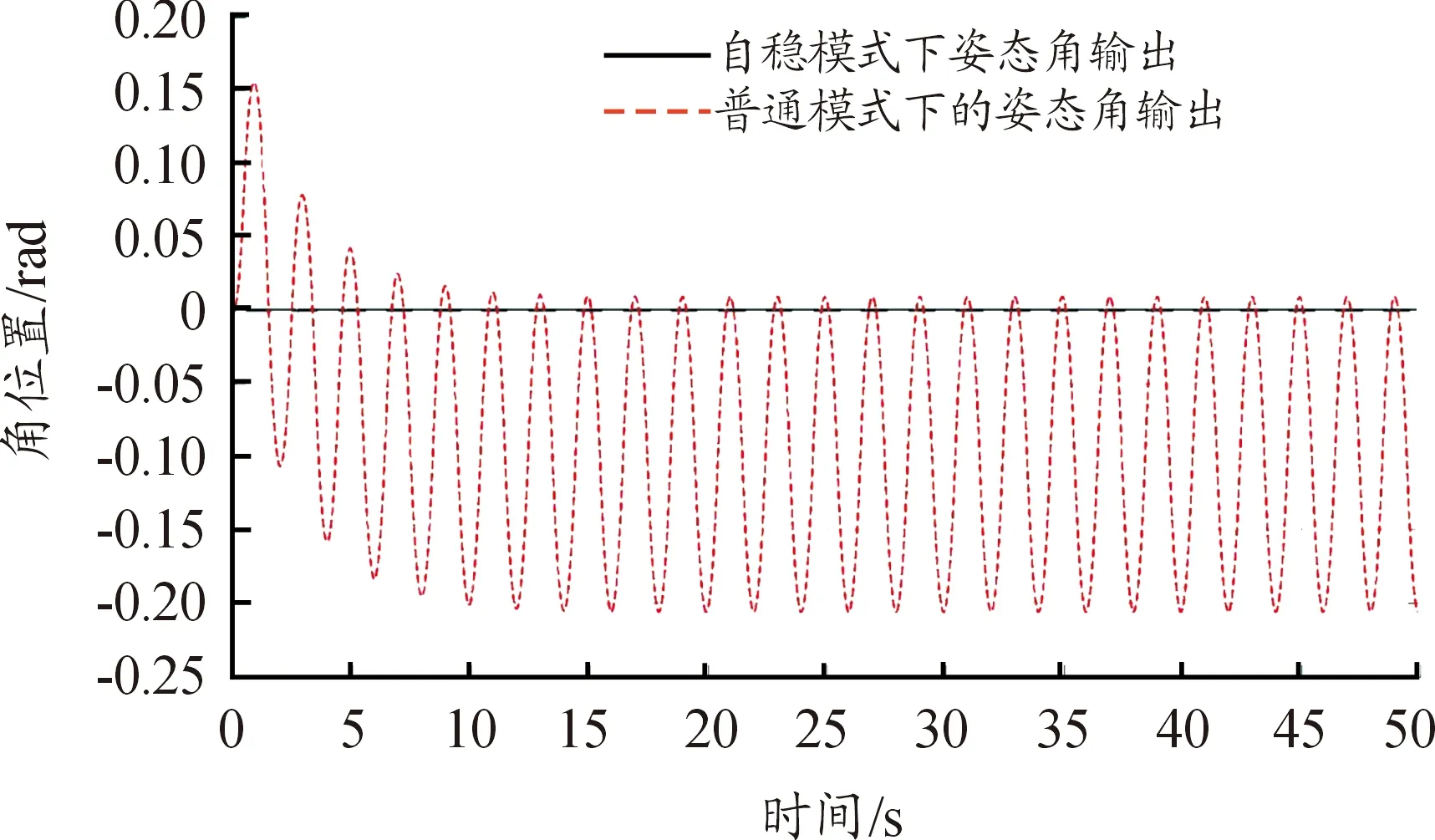
图10 高幅低频干扰信号下的云台姿态角输出曲线
5 跟踪模式
跟踪模式的主要工作原理:首先,通过图像处理捕捉到目标;然后,将带有目标特征的图像传输到图像处理器中进行解析,得到图像中的偏差坐标值;之后,将偏差坐标值通过云台控制系统进行处理,得到机载云台相对惯性坐标系所应调整的俯仰角度与偏航角度;然后,通过伺服电机,基于陀螺仪反馈控制云台转动到指定位置,并通过陀螺仪反馈的飞机振动信号对云台进行隔振控制,使枪械稳定地指向目标,实现准确打击。跟踪模式下机载云台的控制原理如图11所示。

图11 跟踪模式控制原理框图
在跟踪模式下,云台角位置信号主要分为两种:第1种为阶跃信号,即当控制者在图像中发现需要跟踪的目标时,选中该目标,图像处理器计算图像中心与跟踪目标的位置差值,并将差值作为最外环的控制偏差输入到云台控制系统,由云台控制系统控制云台载荷转动,直至图像中心指向跟踪目标后进入自稳模式;第2种为连续信号模式,当需要跟踪的目标在图像中移动时,图像处理器需持续计算坐标偏差并进入到云台控制系统,控制云台跟随转动。
与手动模式相比,云台控制系统的输入量由手动模式的相对于无人机体的角速度指令变为相对于惯性系的角位置指令。
跟踪模式的控制方式与自稳模式类似,不同的是将云台姿态角的输入信号改为阶跃信号或连续信号。因此,基于图7所示仿真程序,更改输入信号为阶跃信号或连续信号,下文将基于这两种信号进行仿真研究。
在1 s时输入幅值为0.5 rad信号的阶跃,无人机抖动信号θ机=0.003 5*sin(10*2*π),忽略云台反作用力对无人机姿态的影响,仿真结果如图12所示。图13为云台稳定后姿态角输入曲线放大图。
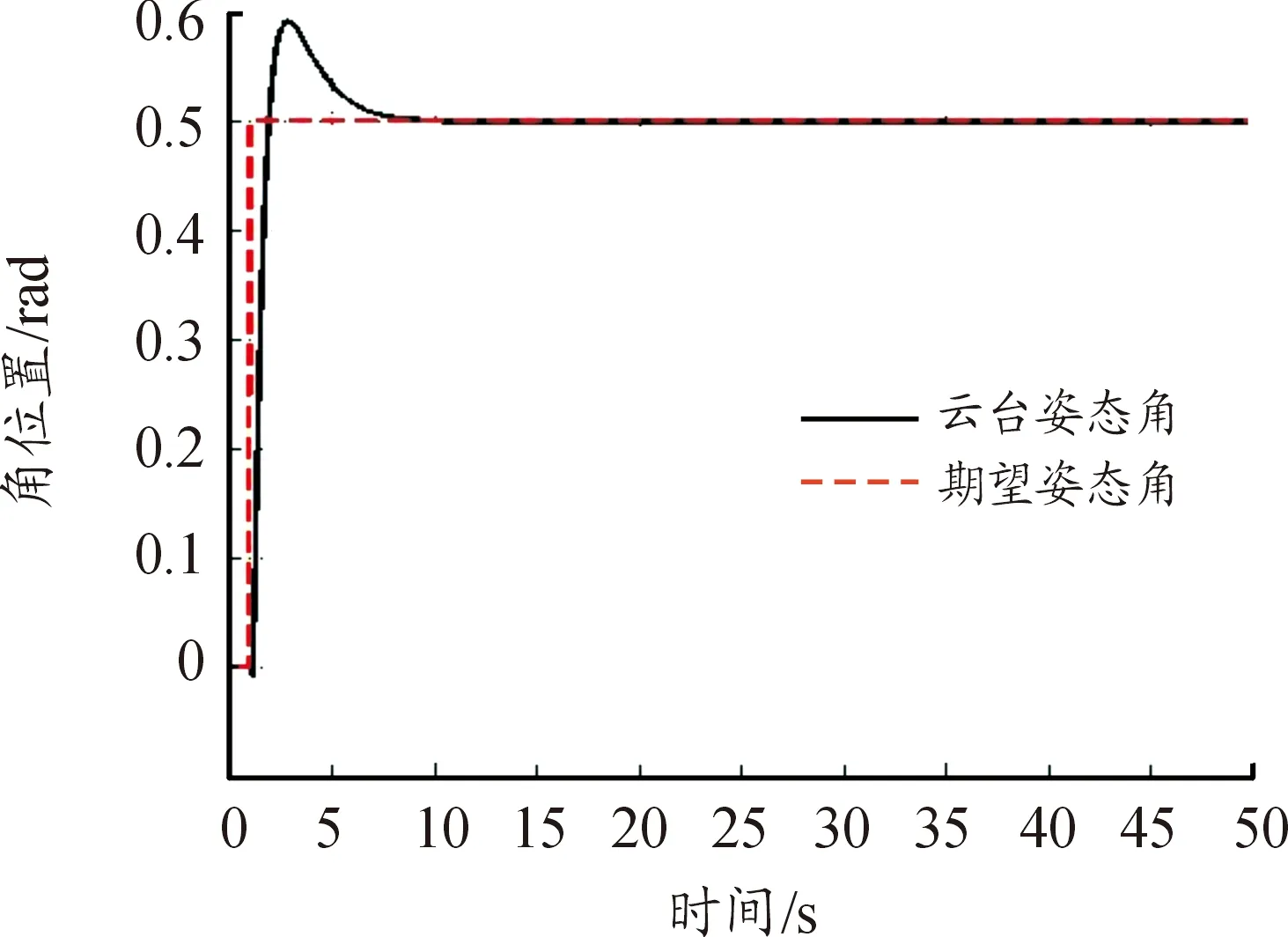
图12 阶跃输入云台姿态角输出曲线
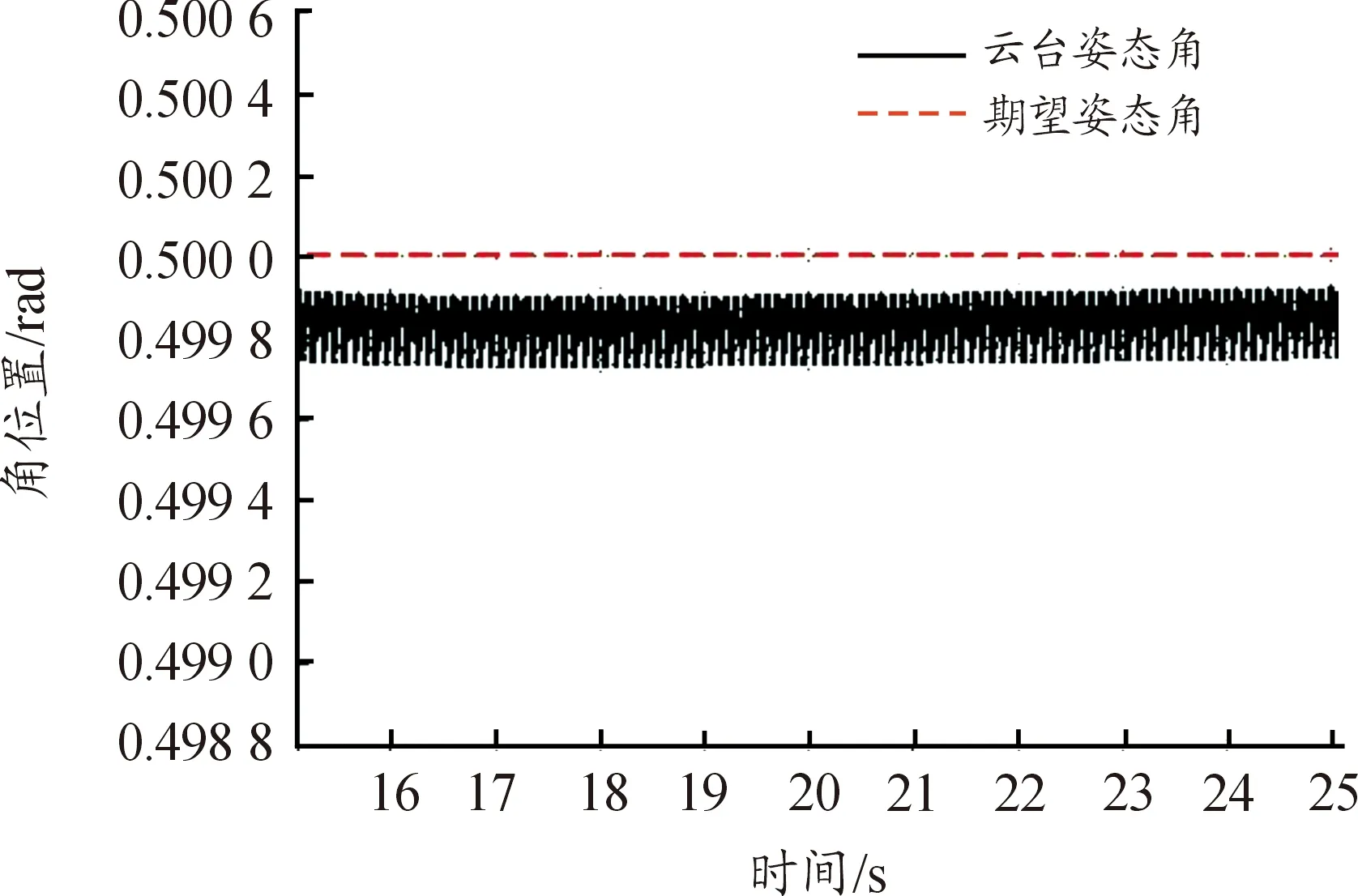
图13 稳定后云台姿态角输入曲曲线
令输入信号为θ=0.5*sin(0.5*2*π),期望姿态角与云台姿态角仿真结果如图14所示。
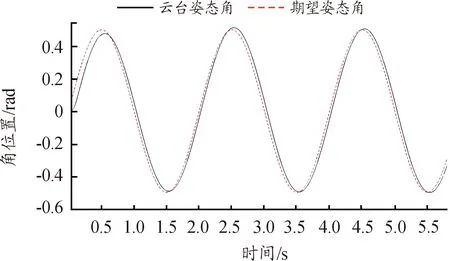
图14 正弦输入的下云台姿态角输出结果
6 结论
提出一种无人机伺服云台的多模式控制及分析方法。基于实际工程应用,设计了无人机伺服云台的手动模式、自稳模式、跟踪模式的仿真及控制方式。手动模式的控制方式为相对于机体坐标系的角速度控制,自稳模式与跟踪模式的控制方式为相对于惯性系的角位置控制。首先基于设计目标,对伺服电机进行选型,选择直流力矩电机作为执行器件,并对直流力矩电机的数学模型进行分析,作为后续速度环、位置环控制的基础。基于所建立的数学模型以及可能存在的外部扰动情况,分别对手动模式、自稳模式、跟踪模式工况下的控制结果进行仿真分析。仿真结果表明:通过所提出的方式分析及控制机载伺服云台可使机载云台保证载荷姿态较好地隔离无人机的外部扰动,使其姿态稳定可控,满足设计的性能指标,并能较快响应角速度、角位置指令。所提出的云台控制与分析方法在实际工程应用中具有参考价值。
