一种德州扑克牌力评估方法

张小川，杜 松，赵海璐，刘 贺，伍 帆

(1.重庆理工大学 两江人工智能学院， 重庆 401135；2.重庆理工大学 计算机科学与工程学院， 重庆 400054)

计算机博弈是人工智能研究中的一个重要领域，以人类所创造的博弈类智力游戏为主，如中国象棋[1]、围棋[2]、二打一扑克[3]、兵棋推演[4]等。非限制性德州扑克作为不完美信息博弈，其博弈状态空间达到10165级别[5]，是一项极为困难的牌类博弈。

近年来，开发顶级德州扑克博弈智能体主要基于以下2种方案：寻找纳什均衡策略[6]、对手模型[7]。2种方案都涉及到牌力评估。反事实遗憾最小化算法(CFR)[8]是求解纳什均衡策略的热门算法。CFR需要计算期望手牌牌力来完成信息集抽象，以此简化博弈状态空间。智能体建立对手模型需要以对手特定牌力时的动作概率分布为依据[9]。牌力也可以直接用作智能体行为决策的依据[10]。优秀的人类玩家必须能够对自身牌力精准地评估，对于计算机博弈智能体而言同样如此。

传统牌力评估方法如TPT(two-plus-two)[11]、Bit Manual[12]、ARS(average rank strength)[13]等，计算数学以领先对手的自然概率作为牌力。这种静态的方法忽略了游戏中的动作信息，且不能针对不同风格的对手调整，导致牌力评估往往不够准确。

为了使智能体对自身牌力有更为准确的认识，提升智能体对抗不同风格对手的实际效益，本文中提出一种方法，通过创建对手模型来辅助牌力评估。该方法充分利用已知信息，使智能体可以根据不同的对手调整自身策略，从而获得更大的收益。

1 背景

1.1 基本概念

德州扑克是2～10人以不带王牌的52张牌进行的扑克游戏。一局游戏有4个阶段：Pre-flop、Flop、Turn、River。Pre-flop阶段每名玩家获得2张手牌仅自己可见，之后的每个阶段分别发出3张、1张、1张公告牌。经过4个阶段的下注后进入摊牌阶段，未弃牌的玩家从公共牌与手牌共7张牌中选出5张组成最大成牌决胜。每个阶段玩家可执行4个动作：Fold、Check、Call、Raise。根据玩家的动作概率分布可以将玩家风格分为凶、弱、紧、松。本文的研究以2人非限制性德州扑克为主要研究对象展开。

游戏中，假定牌桌上所有的牌的集合为Δ，玩家的手牌集合为Φ，场上的公共牌的集合为Ω，任何一位玩家的手牌不会与公共牌重合。排名值函数可定义为Rank=f([Δ]5)。玩家从手牌与公共牌的合集中选出5张牌的组合，该组合的排名值是最大的。该过程可由式(1)表示：

Rank=max({∀x∈[Φ∪Ω]5∶f(x)})

(1)

排名值可类比为一手牌的得分，当牌局进入摊牌阶段时，得分最高的玩家将赢得所有筹码。牌力表示玩家的排名值大于其他未弃牌玩家的概率，取值在0～1。简言之，牌力是一个玩家在摊牌阶段中获胜的概率。

1.2 牌力评估算法

通常，牌力值的计算使用式(2)[14]：

(2)

式中：Total、Ahead、Tied分别表示对手手牌可能的组合总数、领先的组合数、排名值相等即平局的组合数；n表示场上对手的数量。在牌局未进行到River阶段时，尚有公共牌未发出，此时需要考虑潜力，使用式(3)[14]来计算有效牌力值。

EHSn=HSn+(1-HSn)×Ppot

(3)

式中：Ppot表示发出新的公共牌后反超或平局的概率。在Flop阶段，有2张公共牌未发出，此时使用式(3)求解有效牌力值需要计算排名值约106次。优化排名值的计算能提高评估算法的整体效率。

TPT[11]算法是一种快速计算排名值的算法。它需要一个250 M大小的查找表。该算法利用嵌套表结构，每个条目存储着当前索引对应的排名值和另一个表，表中包含所有后续状态。以每张牌的信息作为索引，可以对应找到包含此牌的排名值和下一个状态，在查找牌的数量n次后可得n张牌所代表的排名值。此处n可以是5、6、7，TPT算法支持5、6、7张牌的排名值直接查找，有效提高了效率。王帅等[12]提出Bit Manual算法以5张牌为基础计算排名值。用一个64位整数表达5张牌忽略花色后的牌值信息，通过简单的位运算判别牌型后，结合排序后的牌值计算出排名值。该方法节约了空间占用，但效率并不高。高强等[15]提出一种基于经验的德州扑克博弈系统架构，在系统的估值核心模块中，设计哈希表存储排名值，通过查询哈希表，比较排名值来快速判别胜负。

一些算法不依据式(3)来评估牌力。Teófilo等[13]提出ARS来替代由式(3)计算得到的EHS值。该算法采用3个10 M的查找表，分别对应3个阶段(Flop、Turn、River)。每个表中存储167种手牌发展成7 462种排名值时对应状态的平均有效牌力值。唐杰等[16]利用卷积神经网络，加入对手动作等因素评估当前局面，将胜负结果作为网络输出，其准确率达到了89%。此类监督学习的方法存在一定缺陷，非完美信息博弈中专家经验可能是不可靠的，因此难以提取深度学习所需的高质量数据。张佳佳等[17]采用深度强化学习，提出一种基于蒙特卡罗采样的算法来计算终结状态的期望胜率与期望奖励，减小不完全信息条件下的数据波动影响。

多数算法旨在优化使用式(2)(3)的计算效率，且默认对手持有每种手牌的概率是一样的。考虑对手动作和行为模式，例如一个谨慎的对手在Pre-flop阶段大额加注，那么他持有AK的概率和27的概率显然是不一样的，且前者应该远远大于后者。因此，本文中通过建立对手模型，结合对手动作信息来估算对手实际持有每种手牌的概率，提高当前状态胜率评估准确性。

2 本文的方法

2.1 行为模式树

用树来存储对手在每个状态下的动作频率，称为对手行动模式树。理论上，模式树的规模越大，越能体现对手更细致的策略模式。然而树的规模越大就需要更多的数据来填充树中结点信息，这在实际对局中近乎不可能。由于希望能够在尽可能少的局数里建立可靠的又足以体现对手行为特征的模式树，因此必须限制模式树高度和深度。由于游戏中下注筹码的多样性，使得状态空间非常巨大。玩家可以下注100～20 000范围的任意筹码量，实际上下注120与下注150仅有细微差别。使用动作抽象方法将近似下注量视为同一动作，减少模式树中的分支结点。游戏规则最多允许玩家在一轮下注中4次Raise，实际游戏中通常一方Raise，另一方Call则进入下一轮。默认双方玩家都不会在一轮中做出2次Raise动作，将模式树的深度限定为3层。至此小规模的模式树结构设计如图1所示。

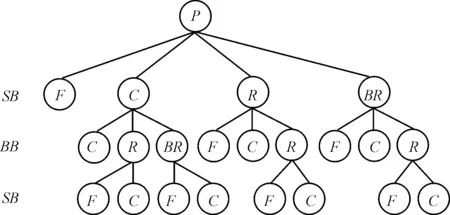
图1 Pre-flop阶段对手模式树结构

与传统博弈树不同，模式树中每个结点均为对手的动作。游戏中每一局后都会轮换大小盲注位置，动作的先后顺序也会随之交换。图1中根节点P表示当前为Pre-flop阶段，第1层中的结点代表对手在小盲位(SB)的所有合法动作，第2层中的结点代表对手是大盲位(BB)，在己方执行相应父节点动作后的选择。C结点代表跟注，R代表加注，BR为大额加注，F为弃牌。所有叶子结点中，F结点的状态为次局游戏结束，C节点代表当前回合结束，进入下一阶段。模式树的结点中保存着对手进入该状态的次数times。

为了分析出对手在各阶段中的策略倾向，需要为4个阶段分别构建模式树。游戏开始时将各模式树中结点的times初始化为0，在对局进行中更新结点信息。更新步骤如下：

步骤1根据当前牌局阶段，选择对应的树的根结点为当前结点S，S中times++。

步骤2根据玩家的动作A，选择S中对应的子结点，将该子结点作为新的当前结点S。

步骤3判断动作A是否是对手执行的，如果是则S中times++。

步骤4判断S是否为叶结点，如果是则转到步骤1，否则转到步骤2。

假设对手不改变自身策略，随着游戏局数增加，树中各结点的times值增大，越能准确体现对手的策略偏向。例如在400局后图1中第2层各结点的times值对应为[16，110，56，18]，可以看出对手在小盲位会倾向于Call，同时有近似8%的手牌会直接弃牌。

2.2 虚拟对手智能体

在游戏中，要凭借已知信息完全破解对手是不可能的，要实现一个智能体能够模仿对手的行为模式做出决策，将其称为虚拟对手。首先需要一个没有任何策略倾向的智能体作为基准，这样的智能体是基于CFR[18]算法求解纳什均衡方法来实现的，其策略称之为均衡策略。理论上，一个采用均衡策略的智能体在对阵任何对手时都可以保证不输，顶尖扑克智能体可以求解近似均衡策略[19]。ACPC[20]比赛官方提供了大量的比赛记录数据，可以通过比赛数据来建立顶尖智能体的模式树。一条比赛记录的格式如下：STATE：6： cr300c/cc/cr1800f：TcTs4d5c/5s2d9c/Th：-300 300： bot1 | bot2。采用2.1节中方法构建顶级智能体的行为模式树，作为均衡模式树基准记为B。

当游戏中与对手进行一定局数(一般为500局)后，对手的行为模式树(记为O)信息开始较为可靠。对于非叶子结点T，每个子结点中times值组成元组(T1，T2，T3)，则有Ts为所有子结点times值总和，归一化处理可得对手在T状态下的行为模式为OT=(T1/Ts，T2/Ts，T3/Ts)。同理求得均衡模式树中T结点下的行为模式为BT，对手的行为偏向GT=OT-BT。

虚拟对手的主要决策算法是一个简单的经验算法，必须快速计算策略才能满足牌力评估的时间要求，此阶段主要是针对对手的一个近似模拟，不需要太高的精度。对于某一具体牌局状态Si，为虚拟对手设定2张手牌，计算出的策略为一个概率分布Pi=(xi，yi，zi)。例如Pi=(0.04，0.36，0.60)，表示在该状态下，对手会有4%的概率弃牌，36%的概率跟注，60%概率加注。当状态Si属于T结点时，实际行动策略根据行为偏向而改变，有P=Pi+GT，至此虚拟对手智能体的策略构建完成。

2.3 牌力评估

当给定手牌和公共牌信息，虚拟对手根据计算出的策略选择一个动作，各阶段动作集合成完整的行动路线。但是由于策略是一个概率分布，相同状态下选择的动作也可能不同，因此虚拟对手给出的策略中执行实际的概率可作为评估对手实际持有该手牌概率的依据。例如在Flop阶段，对手的所有可能手牌为47张牌任意2张组合共 1 081种。令W=(w1，w2，w3，…，w1 081)，所有w值对应手牌的权重，权重wi越大，对手持有对应手牌hi可能性就越大。当前信息包括自身手牌K4，公共牌3Q4，对手为小盲注，所有动作记录为r300c/cr600c。依靠算法1更新权重后，一些与公告牌无关的组合的权重会变得较低，比如虚拟对手持有T7在连续2个阶段下注的概率是较低的，其相应的权重会更新为2个较小的概率的乘积。一些带Q的组合如QJ对应的权重则会相应较高，因为虚拟对手的策略中加注的概率会较大，其行动路线更加符合实际2次加注。

算法1

define update_w：

初始化W=(1，1，1…1)，牌局状态S；

For eachain 动作记录 do：

Ifa是对手执行的do：

For eachhiin opponent_hands do：

计算S虚拟对手策略P;

wi=wi*P(a);};

End For

End If

更新牌局状态S;

End For

每次对手执行动作以后，可以更新W中的权重。

算法2以式(2)为基础，根据W可计算牌力值。初始时权重均为1，此时算法2退化为计算数学上获胜的自然概率。通过对手动作信息来更新W后，计算出的牌力值相对可靠。在公共牌没完全发出之前，还需考虑潜力值，此时使用式(3)结合蒙特卡洛模拟计算有效牌力值。由于德州扑克中花色没有大小之分，2个算法中迭代对手可能的手牌的过程会出现很多重复的计算，通过存储计算历史，可以减小计算耗时。

算法2

define compute_HS：

初始化ahead=tied=behind=total=0;

//使用TPT算法求排名值

self_rank=TPT(self_hand+common_cards);

For eachhiin opponent_hands do：

total=total+wi;

op_rank= TPT(hi+common_cards);

if(self_rank>op_rank)

ahead=ahead+wi;

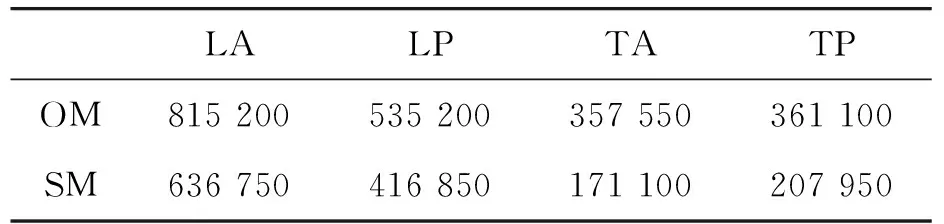
else if(self_rank

behind=behind+wi;

else

tied=tied+wi;

End For

HS=(ahead+tied/2)/total

3 实验结果与分析

为验证基于对手模型的牌力评估方法针对不同对手的有效性。设计了4个风格迥异的对手进行对局实验。对手风格的分类基于专家知识，在文献[9]中也有相关描述，“松”指玩家会以大范围的手牌进入翻牌圈，与之相反的是“紧”，这类玩家在持有胜率较低的起始手牌时会弃牌。“凶”则代表了玩家的激进程度，“弱”为保守程度，与下注攻击对手的频率有关。

通过分析全国博弈大赛的对局记录，选择对手倾向的参数配置如表1所示，4个对手均采用同一决策方法计算基准策略P，然后添加倾向得到在实际博弈状态中采用的策略P′。实验对手在大量博弈中即可表现出明显的风格特征，表1中“松凶”型对手会玩绝大多数手牌，在翻牌前主动弃牌的概率会小于%5，面对加注时也更倾向于跟注。如果翻牌后行成一对或者更强的牌，便会疯狂的加注。而“紧弱”型与之相反，会大概率弃掉不好的牌，且很少会主动加注。表1中的4个对手都有一定程度的缺点，以此来观察使用对手模型评估方法的智能体能否有效针对不同的对手以获得更大的收益。

表1 实验对手参数设置

设置实验对照组智能体SM，它采用静态的牌力评估方法。因建立对手模式树需要一定量的对局数据，在与对手的前500局游戏中，OM也采用静态评估方法。500局以后，对手模式树中的数据足够可靠，OM采用本文的方法继续对局。除了评估方法以外，OM与SM的架构均相同，在实验中2个智能体分别与表1中的4个对手分别进行5 000局，游戏盲注级别设置为50/100，筹码上限 20 000，每局结束重置筹码量。对局结果如表2所示。

表2 对局结果

表2中显示的各智能体5 000局后的累计盈亏筹码量，在面对不同对手OM的收益均高于SM。TA和TP是2个谨慎的对手，弃牌的频率较高，因此无法获得较大的收益，但OM在掌握对手谨慎的风格后，可以更精准地推测对方手牌范围，使得其收益相较SM提高近1倍。LP和LA弃牌较少，所以其最后输掉的筹码较多，他们的手牌范围很大，建立对手模型的效果有所降低，OM的收益提升较小。图2为OM和SM与LA对局的平均每局收益折线，SM在2 000局时可能由于随机发牌的运气因素收益有波动，而后趋于平稳。而OM在1 000局后，收益稳定上升，原因是此阶段对手的行为模式树构建逐渐完善。2 000局后收益趋于平稳，说明此时已经充分掌握了对手的特点，从而获得稳定的收益。

图2 SM和OM对抗LA平均每局收益折线

4 结论

提出的德州扑克牌力评估算法通过牌局信息构建对手行为模式树，分析对手各阶段的行为偏向，计算对手可能的手牌概率分布，完成牌力评估。实验结果显示，基于对手模型的评估方法的效益明显高于静态方法，使用本文方法的智能体可以有效地针对不同风格的对手获得更大的收益，该智能体在2020年全国计算机博弈锦标赛中获得一等奖。本文方法存在的缺点是在面对陌生对手时必须先收集对手信息，不能在游戏初始的对局中使用。如果对手在对局中采用的是混合的策略，模式树对于对手风格的分析会存在不可避免的偏差。后续的研究工作重点在于快速判断对手类型，针对混合策略的对手改进对手模型。