铝合金液态模锻流变充型能力预报模型
2021-10-19邢书明
王 营, 邢书明
(1. 郑州工程技术学院 机电与车辆工程学院, 河南 郑州 450044; 2. 北京交通大学 机械与电子控制工程学院, 北京 100044)
合金熔体的充型能力对成形工件的质量和性能有着非常重要的影响,充型能力直接影响成形铸件的完整性及所得工件的表面粗糙度,所以充型能力一直是材料成形领域关注的焦点问题[1-4]。合金熔体“流变充型能力”与经典的“充型能力”是不同的,流变充型能力是一种考虑流动与变形的充型能力。合金熔体的流变充型是指压力作用下合金熔体依靠自身特有的流变性进行充型的过程[5],在该过程中形成的固、液共存半固态合金熔体具有剪切流变特性[6],进而影响其流变性能。这种特有的剪切流变特性是流变充型区别于流动充型的根本原因。XING等[4]利用变直径的多孔模具研究了半固态合金在压力作用下的充型能力,提出了充型长度的理论计算公式,但是该公式有一定的局限性,主要适用于固相分数较高的半固态坯料。ZHANG等[7]结合不可压缩黏性流体的流变理论和流变充型条件,建立充型能力理论模型。但是该模型没有考虑合金熔体在流变过程中因凝固带来的流变抗力,因此造成误差较大。谭建波等[8]针对半固态A356铝合金建立圆管内流变充型极限长度的数学模型,该模型考虑工艺参数及材料的自身特性,但该模型是针对经过预处理的半固态合金熔体。WANG等[9]建立一个准确描述和预测具有良好孔隙分布的半固态泡沫铝合金的充型模型,该模型是基于固相、液相、气相三相共存的半固态泡沫铝合金的充型过程,该过程既不是液态成形时牛顿体的流动充型过程,也不是固态成形时的塑性变形过程,而是黏塑性非牛顿流体的流变充型过程,因为混合浆料是由悬浮在合金熔体中的固体颗粒和气泡组成的[10]。该模型基于流变充型过程中流变驱动力与流变阻力的动态变化过程,为流变充型距离的模型研究提供了重要参考。MA等[11]根据驱动力被耗尽而使合金熔体停止流动的条件,基于稳态流变行为建立了铝合金熔体/半固态浆料压力驱动充型模型。该模型全面考虑了液态和半固态合金熔体的充型过程,并且也考虑了半固态合金熔体的剪切变稀的流变特性。然而实际上驱动力未被耗尽前,合金熔体即停止流变,因为半固态合金熔体存在临界流变应力,当驱动力不能够克服该临界流变应力时,合金熔体即停止流变,因此该理论模型预测的充型距离要比实际值大,有一定的局限性。
本文针对图1所示的间接加压流变成型方法,其工作过程为合金熔体在压头作用下从压室经直浇道进入型腔。p0为压头作用于合金熔体的流变驱动力,即加压位置的比压;u0为压头运动速度;H1为液面距压室顶面的高度;H为压头运动距离;D为压室直径;D0为直浇道厚度。图1所示的间接加压流变成型方法中,合金熔体是包括纯液态、固液共存半固态的非均质复杂结构,基于非牛顿流体的流变模型和温度、压力的沿程衰减,建立了铝合金液态模锻流变充型距离数学模型。并采用6066铝合金通过间接液态模锻的阿基米德螺旋线试样长度验证模型的有效性。该模型包含加压流变成型工艺参数、材料性能参数及模具结构参数,可以用来预报具体工艺条件下的极限充型长度。
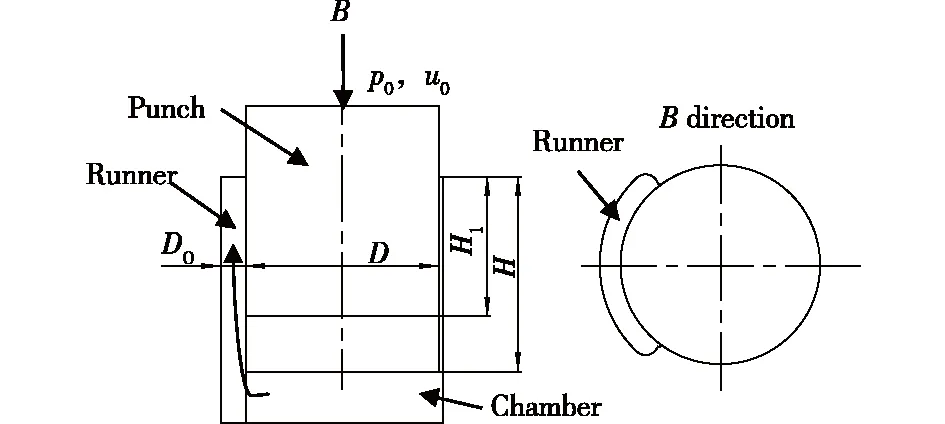
图1 间接加压流变成型示意图Fig.1 Schematic diagram of indrect pressurized rheoforming
1 停止流变机理
液态模锻过程中的流变充型驱动力来源于压头作用于合金熔体的压力p0,而流变充型阻力则包括流变充型过程中的沿程压力损失pf、糊状区由凝固收缩引起的枝晶间液体流动所带来的压力降pfi及合金熔体自身的流变阻力τc(临界切应力)。合金熔体在流变过程中,压头压力p0保持不变,而沿程压力损失pf、凝固收缩带来的压力降pfi及合金熔体自身流变阻力τc均随流变距离l的增大而增大,因此不同流变距离处的应力水平不同,如图2所示。
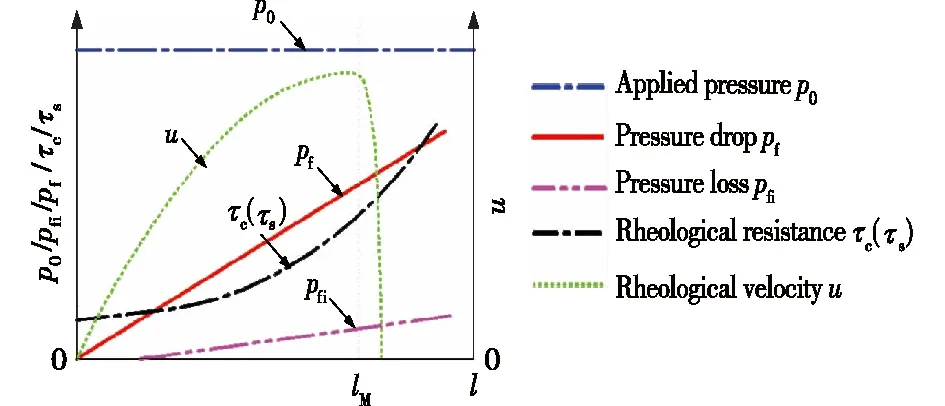
图2 压力/流变速度与流变距离的关系Fig.2 Dependence of pressure/rheological velocity on rheological distance
加压流变过程中,一方面随着凝固的进行,合金熔体温度逐渐降低,流变阻力τc逐渐增大,温度越低流变阻力越大;另一方面随着远离铸件起点距离的增大,压头作用于合金熔体的流变驱动力p0随着流变充型过程中压力损失而逐渐减小。在流变初期,流变驱动力能够克服流变阻力,合金熔体的速度从零开始增大,流变过程持续进行,而随着流变距离的增大及合金熔体温度的降低,外摩擦力及合金熔体的流变阻力均沿程增大,即流变阻力逐渐增大,当其与流变驱动力相等时,合金熔体的速度达到最大,此后因合金熔体流变阻力急剧增大,引起流变速度快速减小,从而使合金熔体停止流变。由此可见只有流变驱动力大于流变阻力τc,合金熔体才可以发生流变,因此,充型过程中包含纯液态和固液共存半固态合金熔体停止流变的条件为
p0-pf-pfi≤τc
(1)
初始条件:压头的运动速度u0视为压室内合金熔体的平均流速,A0,A1和A2分别为压室、直浇道和模具型腔的横截面积,根据流体的连续性方程得合金熔体在直浇道内的平均流速为
u1=A0u0/A1
(2)
合金熔体在模具型腔内的平均流速为
u2=A0u0/A2
(3)
假设合金熔体在模具型腔内充填的长度为x1,根据等体积原理得
A2x1=A0(H-H1)
(4)
2 流变充型距离数学模型的建立
2.1 流变充型过程的温度演变
根据能量守恒定律和傅里叶导热定律得一维常物性、有内热源的能量方程[12]
(5)
式中:ρ为流体密度,kg/m3;C为流体比热容,J/(kg·K);u为流体速度,m/s;λ为流体导热系数,W/(m·K);T为温度,K;t为时间,s;∂T/∂t代表非稳态项;u(∂T/∂x)代表对流项;λ(∂2T/∂x2)代表扩散项。
圆管内流动传热问题可作如下假设:①流动是一维流动;②流变过程中的平均速度为常数;③温度在液相线以上,金属液被认为是牛顿流体(Newtonian fluid),而在固液相线间金属液被认为是具有临界剪切应力的宾汉流体(Bingham fluid),温度低于固相线时认为是塑性体,因此合金熔体在流变过程中看作是牛顿体-宾汉体-塑性体的并联组合;④黏性耗散产生的耗散热可以忽略不计。该传热过程包括金属液与圆管壁面C的流动换热和自由端面B的自由换热,但由于圆管横截面积较小,自由端面的自由换热可忽略不计,其流动传热示意图如图3所示。
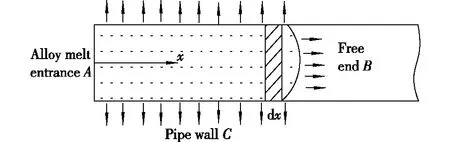
图3 圆管内流动传热示意图Fig.3 Schematic diagram of flow and heat transfer in a round pipe
内热源包括结晶潜热和通过壁面的散热,因此单位体积合金熔体的热源为
(6)
式中:L为结晶潜热,J/kg;d为流变管道内径,m;T0和T分别为铸型温度和任意时刻金属液的温度,K;h为金属液与铸型的换热系数,W/(m2·K),换热系数h与外加压力p0(MPa)间的经验关系[13]为h=0.001 1p03-0.112p02+6.605p0+2 924.57。式(6)带入一维常物性、有内热源的能量方程(5)整理得微分方程为
(7)
式中:u为合金熔体在流变过程中的平均速度,m/s;a为合金熔体的热扩散系数,m2/s,其表达式为a=λ/(cρ);x为流变距离,m。
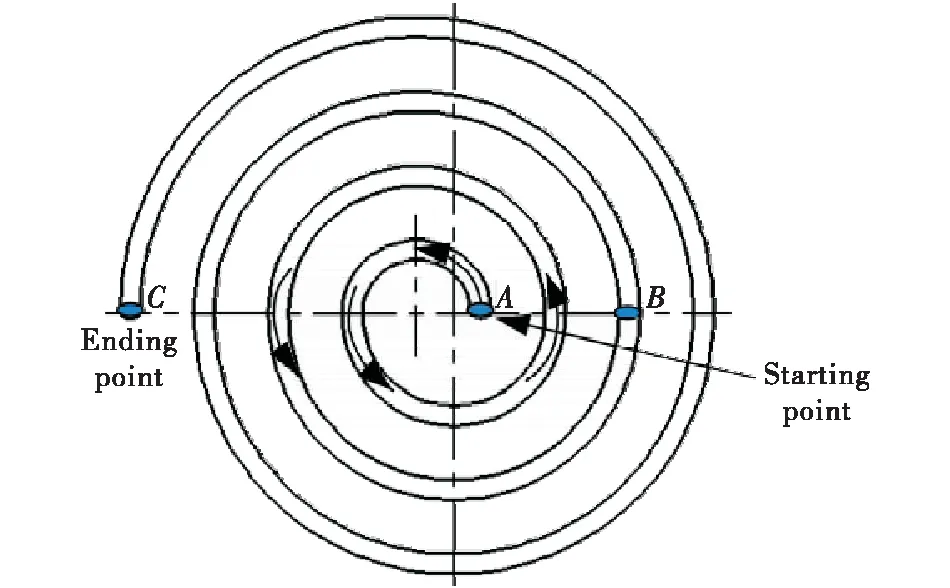
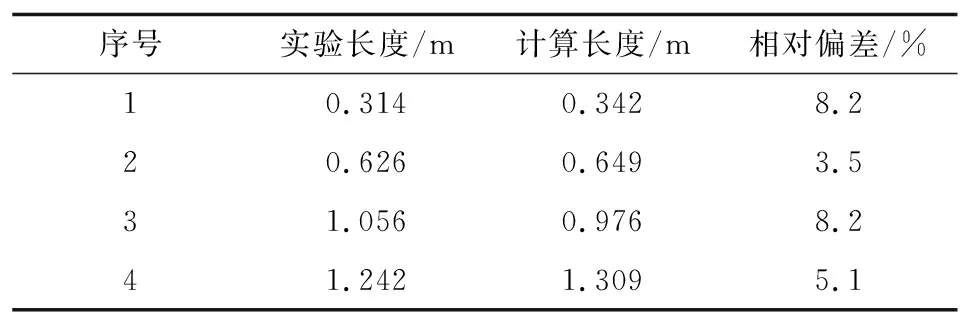
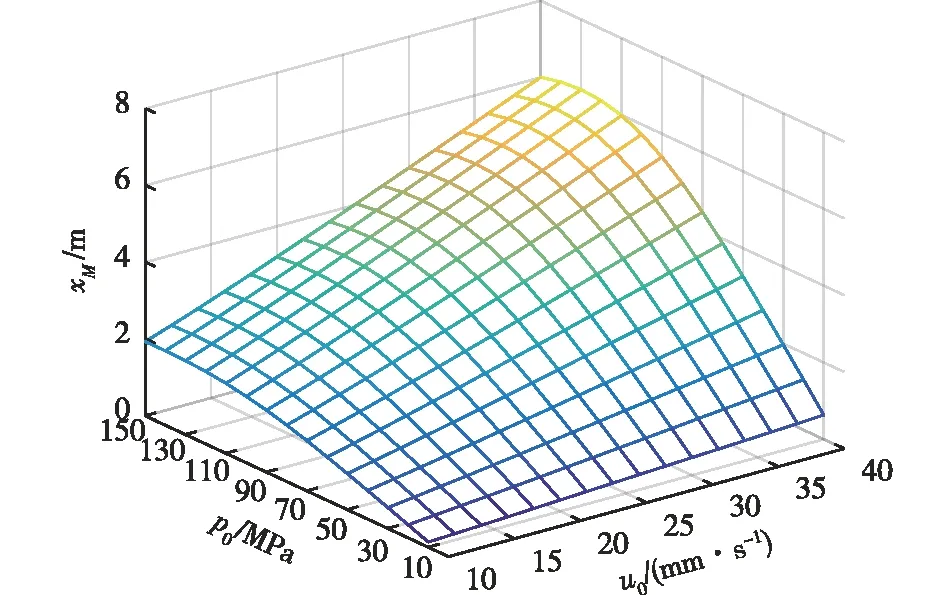
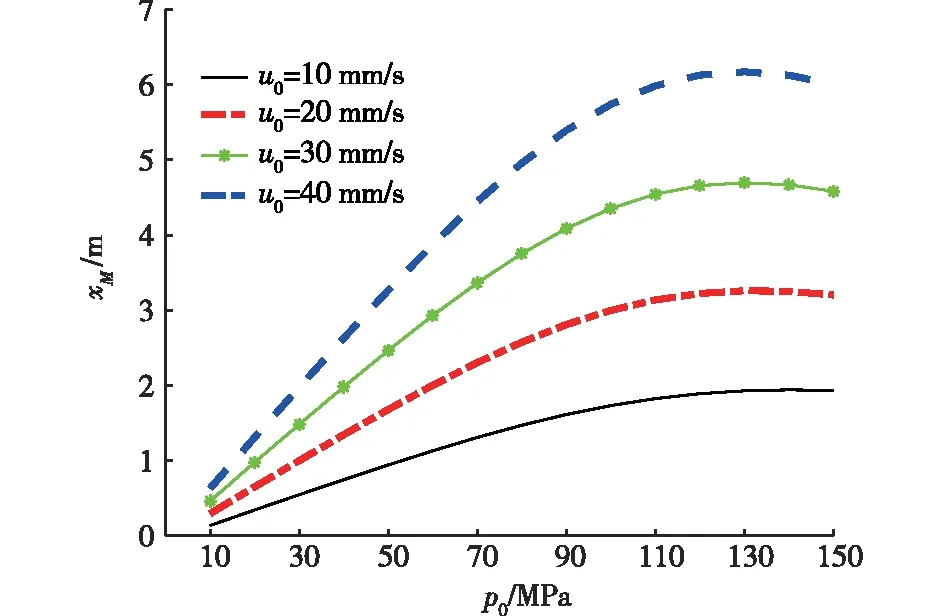
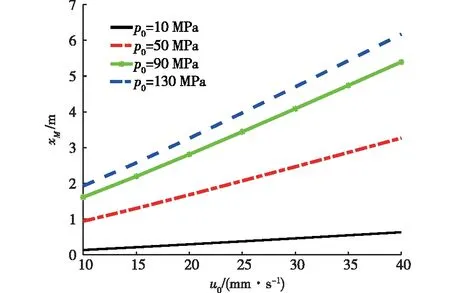
合金熔体在流变凝固过程中,假设TL和TS分别为材料的液相线和固相线温度,则固相分数fs的演变过程为:当T≥TL时,fs=0;当TS 当T≥TL时,初始条件为x=0,T=TJ(TJ为浇注温度),t→ ∞,T=T0+LρLd/(4h),ρL为液相密度,通过谐波法[14]求解微分方程(7),得合金熔体温度的沿程变化规律为 (8) 当金属液温度降至液相线以下直至停止流变(停止流变时的温度为TK),即TS (9) 引入固相分数fs,固、液混合半固态合金熔体的平均密度和平均导热系数分别为ρ1=ρsfs+ρL(1-fs)和λ1=λsfs+λL(1-fs),其中ρs为固相密度,kg/m3;λs和λL分别为固相和液相的导热系数,W/(m·K)。 根据泰勒公式,式(8)和式(9)中的eβx可表示为1+(βx)/1!+(βx)2/2!+…+ (βx)n/n!+…,对于工程实际中常用的如镁合金、铝合金及钢铁材料等金属材料,其物性参数为C=470~1 020 J/(kg·K),ρL=(1.73~7.87)×103kg/m3,λ=37.2~192 W/(m·K)140,取h=450 W/(m2·K)143,一般流变距离x<5 m,βx<1,因此略去2次以上的高次项对计算结果影响不大,为简化计算,式(8)和式(9)略去2次以上的高次项后,得温度的沿程变化规律见式(10),为 (10) 由式(10)可以看出,随流变距离的增大,合金熔体温度呈线性规律逐渐降低。 由液相、固相和固液混合物组成的金属熔体的流变行为极其复杂,它们共同的特点是存在一个临界应力,只有当外加应力大于这一临界应力,这种混合物才能发生流变。因此,这一临界应力称为流变阻力。且随着流变距离的增加,合金熔体温度逐渐降低,临界切应力逐渐增大。在较小的温度范围内,假设合金熔体的剪切流变阻力τc与温度T成线性关系[14],即 (11) 式中τst表示固相线温度TS时的流变阻力,MPa。 针对图1所示的间接加压流变成型方式,式中的u为式(3)中的u2,式中的x=H1+x1,将式(10)带入式(11)得流变阻力与流变距离的关系为 (12) 由于式(12)中β1<0,所以随流变距离的增大合金熔体的流变阻力τc呈线性规律逐渐增大。 合金熔体的流动状态分为层流和紊流,可以根据雷诺数Re来判断。对于牛顿流体雷诺数定义式为Re=ρdu/η。η为流体的动力黏度,MPa·s,对于非牛顿流体用表观黏度ηeff=η0(1+2.5f+6.2f2)[15]来表达。一般认为,雷诺数Re小于2 300视为层流流动,大于4 000视为紊流流动,而介于2 300和4 000之间,视为层流和紊流的过渡状态。液态模锻等加压流变成型中不允许出现紊流,都是层流,故只分析层流流动。对于非牛顿流体的层流流动,可借鉴牛顿流体压力降的表达方式,写成阻力系数或摩擦因数的形式,见式(13) (13) 式中:pi为流体的沿程压降;ξ为沿程阻力系数,是雷诺数和管子相对粗糙度的函数,即ξ=f(Re,Δ/d),其中,Δ/d为管子的相对粗糙度,Δ为管子的绝对粗糙度;x为流体流经的距离。 非牛顿流体的黏度较大,采用光滑管的计算能满足工程要求,即阻力系数计算时,可不考虑管子粗糙度的影响,用雷诺数Re表示沿程阻力系数ξ=64/Re。 合金熔体通过压室、直浇道和型腔的沿程压降分别为p1,p2和p3,为 (14) 合金熔体从压室流入直浇道再进入模具型腔,因流速方向及空间位置的改变,带来了附加阻力,从而增加能量损失,该部分损失通常称作局部阻力损失,表达式为 pj=Kjρu2/2 (15) 式中Kj为局部阻力系数。熔体从压室流入直浇道时Kj=k(1-A0/A)2,式中k为修正系数,参照管径突然收缩和急转弯管的局部阻力系数,一般取k=0.50~1.75。于是合金熔体从压室流入直浇道和从直浇道流入型腔的局部阻力损失分别为p4和p5,为 (16) 结合式(4),综合以上各种压力损失得合金熔体通过压室、直浇道和型腔的总压力降pf为 (17) 加压流变成型过程中,随着凝固的进行,合金熔体温度逐渐降低,流变阻力τc逐渐增大;另一方面随着流变距离的增大,压头作用于合金熔体的流变驱动力p0因外摩擦力的增大而逐渐减小。不考虑凝固收缩带来的压降,当流变驱动力减小到不能够克服流变阻力而停止流变时,螺旋线型腔内的充型长度xM即为流变充型距离。如图4所示,螺旋线型腔横截面考虑为圆形,从螺旋线起点A沿箭头方向流变到某一位置B处流变停止,从点A到点B的距离即为流变充型距离xM。不考虑凝固收缩引起的压降,将式(12)和式(17)带入式(1),整理得式(18),为 图4 螺旋线型腔内的流变充型距离Fig.4 Rheological filling distance in spiral cavity (18) 令式(18)取等号(x1=xM),解得流变充型距离xM为式(19) (19) 实验材料选用Al-Mg-Si系的6066变形铝合金,其化学成分见表1[16]。固相线温度836 K,液相线温度918 K,其他材料性能参数见表2[17]。 表1 6066铝合金的化学成分 表2 材料性能参数 实验采用的螺旋线试样模具如图5所示,模具的主体部分包括压头、上模、下模和压室4部分。液态模锻过程工艺参数为压头运动速度u0分别为10,20,30,40 mm·s-1,比压p0为20 MPa,浇注温度TJ为993 K,模具温度T0为373 K,浇注量为1 kg,所得到的螺旋线试样如图6所示。采用阿基米德螺旋线试样的充填长度作为流变充型距离的度量。 图5 螺旋线试样模具Fig.5 Mold of spiral sample 图6 螺旋线试样Fig.6 Spiral sample 由式(19)可知流变充型距离与材料性能、工艺过程、流道结构及微观组织等参数密切相关,在给定材料情况下,微观组织参数为动态变化的过程参数,因此可以通过改变工艺过程参数及流道结构来改变材料的流变充型距离。根据式(19)计算得到流变充型距离与间接液态模锻成型的阿基米德螺旋线试样长度进行对比,如图7所示。 图7 理论计算结果与实验结果的对比Fig.7 Comparisons between theoretical calculation values and experimental results 为展示模型计算结果与实验结果的吻合程度,进一步做了相对偏差分析,见表3。结果表明:理论计算结果与实验数据吻合较好,其最大相对偏差仅为8.2%。产生该偏差的原因主要有:①理论计算中,将型腔简化为直管,忽略了型腔内的局部损失,合金熔体的剪切流变阻力与温度在较小范围内假设为线性关系,与实际存在一定偏差等;②实验过程中浇注温度、模具温度的偏差,涂料喷涂的均匀性,液压机的压力波动等。 表3 理论计算结果与实验结果的偏差分析 ZHANG等[7]根据充型驱动力不小于合金熔体充型时的摩擦阻力和局部阻力之和建立理论模型的最大相对偏差高达15%,由此可见本文基于非牛顿流体流变驱动力不能克服流变阻力而建立的理论模型具有一定的进步性。谭建波等[8]虽然也从流变角度建立了充型极限长度理论模型,但该模型针对经过预处理的固相为近球形颗粒的半固态合金熔体,使用范围受到一定的限制。 通过式(19)的理论模型分析可知充型压力和充型速度是影响流变充型能力的两个主要因素,为了直观展示它们的影响规律,基于上述模型参数,进一步计算了充型速度和外加压力对流变充型距离的影响规律,结果如图8所示。结果表明随着充型速度u0(mm·s-1)和压力p0(MPa)的增大流变充型距离xM(m)均增大,为更清楚的反应该规律,以下分别对充型速度和压力对流变充型距离的影响规律进行详细分析。 图8 流变距离与充型速度和压力的关系Fig.8 Dependence of rechological distance on filling velocity and pressure 针对该理论模型分析不同充型速度下压力的变化对流变距离的影响规律,如图9所示。可以看出,不同充型速度下流变距离随着p0的增大逐渐增大,且增大的速度逐渐减小,当p0达到130 MPa时,流变距离不再继续增大,且随着压力的继续增大稍有降低的趋势。产生该结果的原因是:增大p0就是增大流变驱动力,在流变阻力等条件不变的情况下提高了合金熔体的流变性能,由图2可以看出,增大压力流变充型距离xM点向右移动,即流变距离增大。由此可见,适当提高外加压力有助于改善合金熔体的流变性能[19],从而增大流变距离,过大的外加压力不仅会造成能源浪费,还将大大降低模具的使用寿命。 图9 给定流变速度条件下流变距离随压力的变化Fig.9 Dependence of rheological distance on pressure at selected rheological velocities 针对该理论模型分析不同压力下充型速度的变化对流变距离的影响规律,如图10所示。可以看出,不同压力下流变距离随着充型速度的增大逐渐增大。产生该结果的原因是:一方面增大流变速度可以缩短流变时间,减少充型过程中的热扩散;另一方面半固态合金熔体具有剪切变稀的流变特性,随流变速度的增大表观黏度降低,两方面综合作用的结果使流变距离增大。由此可见,适当提高充型速度有助于改善合金熔体的流变性能[8],从而增大流变距离,而当流变速度增大到一定程度,合金熔体的流动状态将会由层流过渡为紊流,这将严重影响铸件的质量,这在液态模锻过程中是不允许的。 图10 给定压力条件下流变距离随流变速度的变化Fig.10 Dependence of rheological distance on rheological velocity at selected pressures 综上可知,流变充型距离理论模型可以方便的分析各工艺参数的变化对充型距离的影响规律,通过该理论模型计算可以发现适当提高外加压力及流变速度,均有助于改善合金熔体的流变性能,从而增大合金熔体的流变距离。但该模型在表达流变与凝固耦合的动态过程方面还存在一定的局限性,有待进一步完善,同时也需要进一步扩大实验范围。 1)揭示了铝合金液态模锻的停止流变机理。随着凝固的进行,铝合金熔体温度逐渐降低,流变阻力逐渐增大,而同时流变驱动力因摩擦消耗逐渐降低,当流变驱动力不能克服流变阻力时,流变速度快速减小而使流变停止。 2) 建立了铝合金液态模锻流变充型距离数学模型。通过谐波法求解一维耦合热传导——热对流方程,得到温度的沿程衰减规律,进而求出流变阻力的沿程增大规律;另一方面求解压力的沿程衰减规律,结合停止流变机理和条件,针对液态模锻铝合金熔体包括纯液态和固液共存半固态的非均质复杂结构,建立了流变充型距离数学模型。 3) 验证实验表明本文的流变充型距离数学模型预报精度更高。采用间接液态模锻成型的阿基米德螺旋线试样长度来验证理论模型的有效性,结果表明:根据式(19)计算得到流变充型距离与实验结果的最大相对偏差仅为8.2%。与现有的充型能力模型相比,本文的流变充型距离模型在预报精度及适用范围方面有一定的进步性。基于流变充型距离数学模型计算表明:适当提高外加压力及流变速度,均有助于改善合金熔体的流变性能,从而提高合金熔体的流变充型能力。
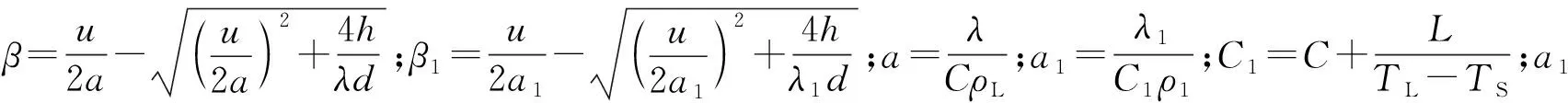
2.2 合金熔体流变阻力的沿程增大规律
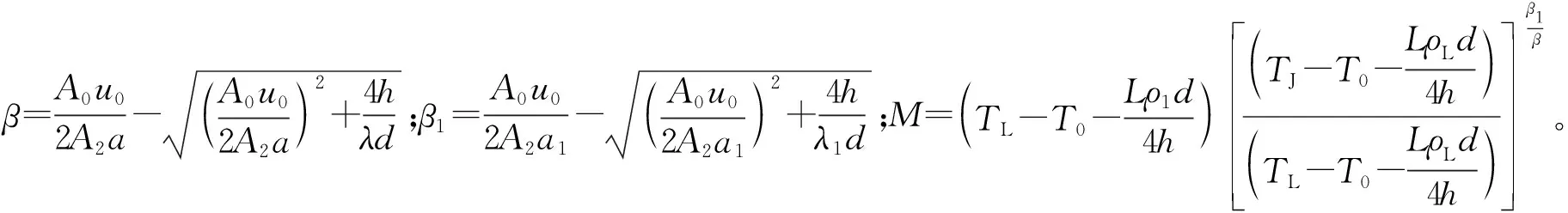
2.3 压头压力的沿程衰减规律

2.4 流变充型距离模型

3 模型验证与分析讨论
3.1 模型的实验验证





3.2 分析讨论
4 结 论
