横向冲击下圆钢管混凝土构件挠度计算方法研究

刘艳辉， 赵一超， 慈伟主,2， 王 喆， 王路明， 朱文凯， 韩达光

(1.西南交通大学 土木工程学院,成都 610031；2.安徽省交通规划设计研究总院股份有限公司,合肥 230088；3.奥斯陆城市大学 土木工程与能源技术系,奥斯陆 0166)

随着结构跨度的增大和层数的提高，钢管混凝土构件在桥梁、建筑中的应用更加广泛。在结构服役期间，钢管混凝土构件可能会遭受如列车脱轨冲击、船只意外冲击等偶然荷载的作用，从而对结构造成破坏或损伤[1-2]。冲击是一种高频高危的极端荷载作用[3]，不仅可能对构件本身造成损伤、破坏，更有可能引起整体结构的损伤、破坏，甚至连续倒塌[4]。所以研究钢管混凝土构件的抗冲击破坏性能，对防止工程结构破坏及连续倒塌，减少生命财产损失具有重要意义。

钢管混凝土构件在遭受横向冲击荷载的作用后，评估其损伤情况，是十分重要的。而对于未断裂构件，其挠度是一个重要的评价指标[5]。因此，如何计算钢管混凝土构件在遭受横向冲击时冲击点处挠度，一直是学者们广泛关注的问题。Bambach等[6]对空心和混凝土方型钢空心截面构件在跨中受到低速横向冲击时的动力特性进行了试验和分析研究，并提出了一套基于力、挠度或能量的方钢管混凝土构件设计方法。Qu等[7]通过LS-DYNA软件进行数值模拟，基于模拟结果建立了固简支条件下钢管混凝土构件跨中挠度简化计算方法，并给出了基于冲击能量、构件长度、截面动力塑性极限弯矩等物理量的固简支构件跨中挠度简便计算公式；在此基础上，Shakir等[8]通过试验研究了普通和再生骨料钢管混凝土柱在侧向冲击作用下的动力响应，并考虑冲击块的形状影响提出了各试验柱的挠度的理论预测方法，与试验结果具有较好的相关性。贾电波[9]进行了圆钢管混凝土构件侧向冲击试验，研究了不同因素对钢管混凝土构件横向挠度的影响，同时对圆钢管混凝土构件跨中撞击挠度进行了理论推导，并给出了基于冲击速度、构件质量、构件长度、截面塑性极限弯矩等物理量的两端简支跨中撞击构件的挠度简化计算公式。王蕊等[10]通过连续性模型，根据弯曲理论进行计算，分别推导出圆钢管混凝土构件在跨中撞击下的弹性阶段和塑性阶段的挠度理论计算公式。宋家欢[11]基于等效单自由度理论推导了一端固定、一端滑动的钢管混凝土构件受跨中冲击最大挠度计算公式；Wang等[12]在此基础上，基于等效单自由度法，提出了考虑轴力影响的简化计算方法，用于预测钢管混凝土柱轴心受压构件在侧向冲击作用下的挠度。然而，目前为止大部分的对挠度的研究都是针对跨中遭受冲击的钢管混凝土构件，在实际的工程应用中，不具有普适性。

为了给工程设计人员提供计算快速、结果可靠、应用广泛的计算方法，本文首先考虑边界约束效应理论推导出任一点冲击下的构件冲击点挠度计算公式，然后基于能量损失和局部变形，通过55组试验数据统计回归分析，拟合得到一个修正公式，用于修正理论推导时各类假定所导致的误差。

1 任意冲击点的最大挠度计算公式

Jones[13]曾利用移行塑性铰模型，将冲击过程分为两个运动相，对两端固支边界条件下的梁跨中冲击的动力响应做了理论推导，但从实际工程来说，冲击的部位是不确定的，构件的边界条件也不只有两端固定。故根据Jones的移行铰模型(在该模型中，塑性铰的位置是可以随时间变化的)，考虑不同边界边界条件，对任一点遭受冲击的构件冲击点挠度计算进行推导，以两端固定约束构件为例,如图1所示。

图1 两端固定构件遭受任一点横向冲击运动示意图

长度为l1+l2的构件在任意点O处受到质量为m1、初始速度为v0的冲击体横向冲击。冲击点在冲击瞬间以速度v0运动，而构件的其余部分保持静止。因此，冲击点处的扰动将向两个支座处传播，直到到达支座为止。然后，构件发生整体弯曲变形，消散剩余的冲击能量，最终停止。上述碰撞过程可分为3个不同的运动相，分别定义为第一相、第二相和第三相。

第一相，t=0时刻，冲击点处生成一个塑性铰，同时，另外两个塑性移行铰将扰动从冲击点向两个支座传播，直到D塑性移行铰率先到达近支座B，形成一个固定塑性铰，不再运动；

第二相，在D塑性铰变为固定塑性铰后，C塑性移行铰继续向远端支座A移动，直到到达支座A，形成一个固定塑性铰，不再运动；

第三相，支座处和冲击点处固定塑性铰均保持不动，构件在冲击能量的作用下继续向下运动，直到构件和冲击块的动能耗尽。

1.1 第一相运动

由图1的模型，当0≤t≤t1，即塑性铰在构件的OB段运动，此时速度场为

(1)

(2)

把式(1)代入式(2)及对t求积分可得

(3)

(4)

由构件C和D两塑性铰之间，取一半对冲击点O取矩，其中，Mp为构件截面极限弯矩[14]

(5)

(6)

(7)

式中：fc为混凝土圆柱体抗压强度；fy为钢管的屈服强度；D0为构件直径;h为钢管壁厚。

对t积分可得

(8)

联立式(4)和式(8)可得，构件任一点的横向位移，其中，w01为冲击点的第一相结束时的横向位移

(9)

(10)

1.2 第二相运动

此时D移动塑性铰与固定端B重合，不再运动，而C移动塑性铰继续向远固定端移动，此时选取AC段进行分析。其中，w02为冲击点的第二相结束时的横向位移，推导过程同理第一相，可得

(11)

1.3 第三相运动

第三相即为冲击动力响应的最后相，该处假设冲击块和构件的剩下的所有动能都能在该相中由塑性铰消耗掉。K为系统的总动能;K1为冲击块的动能;Kl2为构件l2跨动能;Kl1为构件l1跨的动能;θ1为l1跨的塑性铰的转角量;θ2为l2跨的塑性铰的转角量，其中

2Mpθ1+2Mpθ2=K

(15)

联立横向位移场和几何关系可得

w=θ1l1

(16)

θ1l1=θ2l2

(17)

联立式(12)～式(17)可得第三相构件的横向位移场为

(18)

上述是针对两端固支边界条件下的三个运动相运动过程理论推导，而对于其他边界条件，比如两端简支边界条件和两端固简支边界条件。由推导过程可知，区别主要在于第三运动相中塑性铰的个数。对应的式(15)可以修改为

简支

Mpθ1+Mpθ2=K

(19)

固简支

2Mpθ1+Mpθ2=K

(20)

为方便计算，此处设立边界系数μ1和μ2，其值与边界条件有关，与两端固支边界条件下的钢管混凝土构件冲击点挠度理论推导过程同理，可将式(18)修改为

(21)

式中，μ1和μ2可根据下列三种边界条件进行相应取值：①两端固支构件，μ1=2，μ2=2；②两端简支构件，μ1=1，μ2=1；③固简支构件，μ1=1，μ2=2。

综上所述，钢管混凝土构件受到横向冲击，其冲击点最大挠度为

w0=w02+w03

(22)

2 不同边界条件下的挠度公式修正

为了验证公式的精度，基于以下两个条件，表1～表4统计了文献[9，15-18]中55根钢管混凝土构件在侧向冲击荷载下的试验结果：①构件在侧向冲击荷载作用下未开裂，以避免构件开裂失去抗冲击能力的影响；②基本材料性能和构件信息完善。

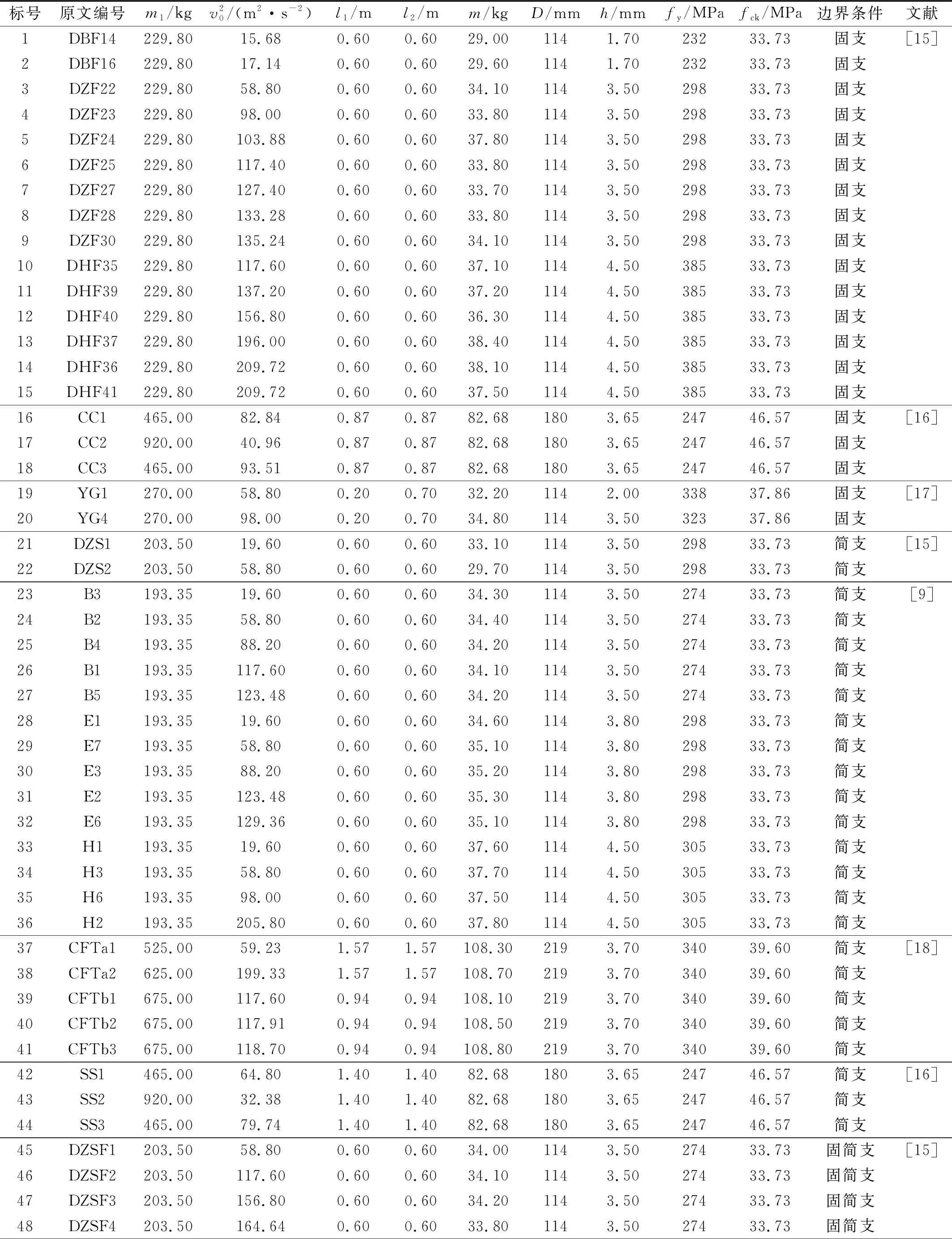
表1 统计的试验构件详细信息

表1(续)

通过计算发现，钢管混凝土构件的计算挠度明显大于试验挠度,如表2～表4所示。这是因为在实际钢管混凝土构件遭受任一点横向冲击的工况中，系统的动能并不是全部由塑性铰耗散的，局部压缩变形、支座边缘钢管屈曲变形以及约束端摩擦也会消耗一定的能量。本文在理论推导时，为了得到清晰的力学现象和冲击点的计算挠度，利用的是简化的刚塑性力学模型，假定所有能量都被塑性铰完全耗散，导致在本文的第三相中计算出来的横向变形明显大于试验值，是一个上限值。因此，需要考虑一个折减系数λ对其进行修正。

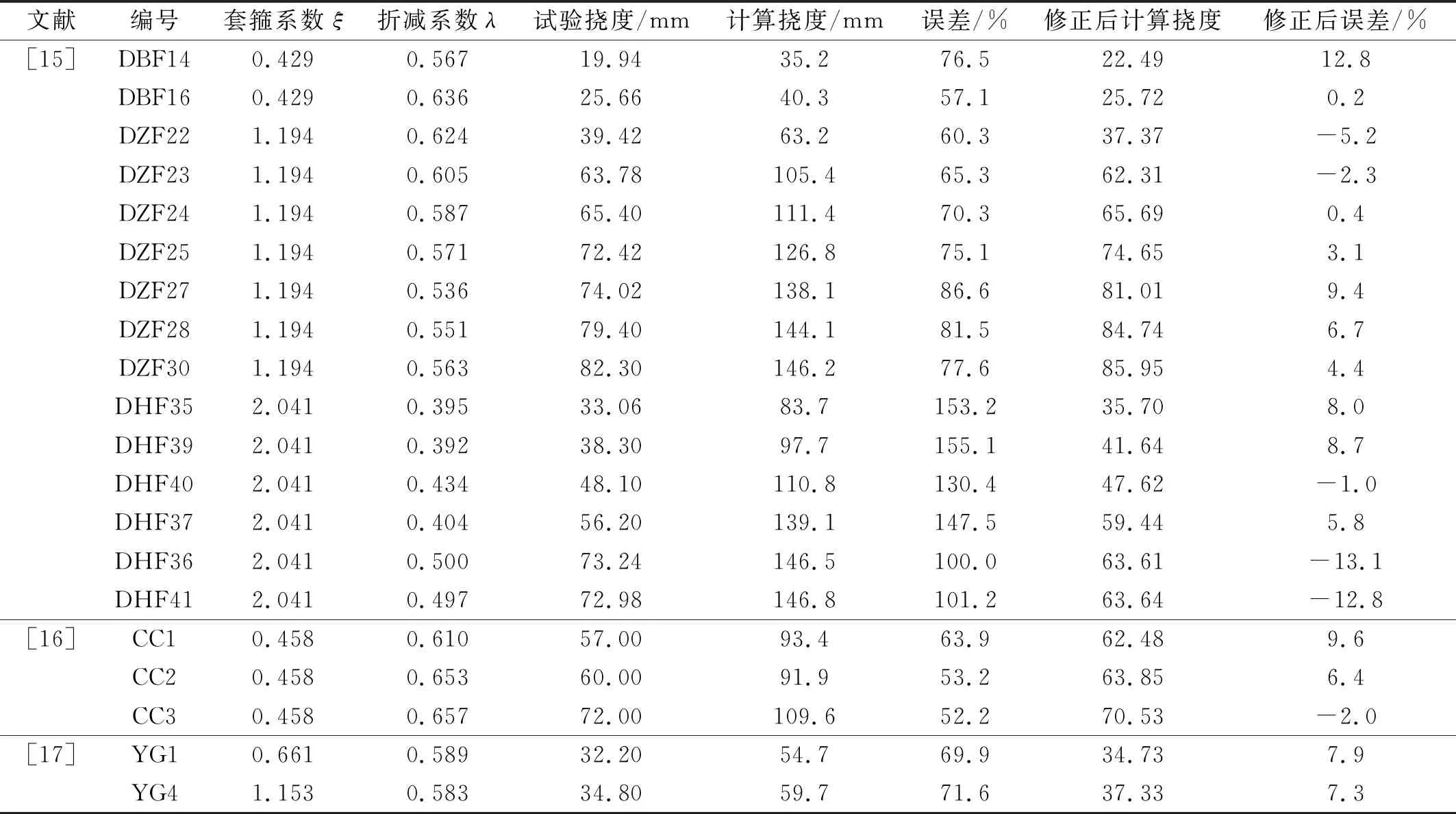
表2 两端固支边界条件构件挠度计算结果

任够平等[19]研究表明，套箍系数ξ、边界条件是横向冲击下钢管混凝土构件挠度的显著影响因素。为了进一步证明套箍系数ξ对折减系数λ的显著性，本文通过对不同边界条件下折减系数λ和套箍系数ξ进行方差分析[20](见表5)，发现对应F值均显著大于F0.01(s-1,n-s)，即因素(套箍系数ξ)对结果(折减系数λ)高度显著，因此可以假定套箍系数ξ是折减系λ的唯一因变量。分别通过回归分析，得到了不同边界条件下，钢管混凝土构件冲击点的计算公式和折减系数。

套箍系数按式(23)计算

ξ=(fyAs)/(fckAc)

(23)

式中：As为横截面钢管面积;Ac为横截面混凝土面积，fck为混凝土轴心抗压强度;fy为钢管屈服强度。

2.1 两端固支边界条件下挠度计算公式

钢管混凝土构件的冲击点最大挠度计算公式可以修正为

w0=w02+λw03

(24)

式中，折减系数λ由统计试验结果回归分析得到。对于两端固支约束构件，表2统计了国内外共20根构件，由统计结果，折减系数λ与套箍系数ξ之间存在一个明显的二次函数关系，即

λ=-0.065ξ2+0.046ξ+0.613

(25)

由图2可知，拟合优度R2为0.82，这表明统计回归模型有效的反映了折减系数与套箍系数之间的变化规律和发展趋势。其中，套箍系数为挠度修正计算公式的敏感因素，样本中ξ取值范围为0.429～2.041。GB 50936—2014《钢管混凝土结构技术规范》[21]规定实心钢管混凝土套箍系数ξ宜为0.5～2.0。故最终挠度修正计算公式的适用范围为ξ=0.5～2.0。

图2 两端固支边界条件下拟合图

2.2 两端简支边界条件下挠度计算公式

同理，得到钢管混凝土构件两端简支构件的冲击点挠度计算公式。表3统计了国内外24根钢管混凝土冲击构件，由统计结果，折减系数λ与套箍系数ξ之间存在一个明显的二次函数关系，即

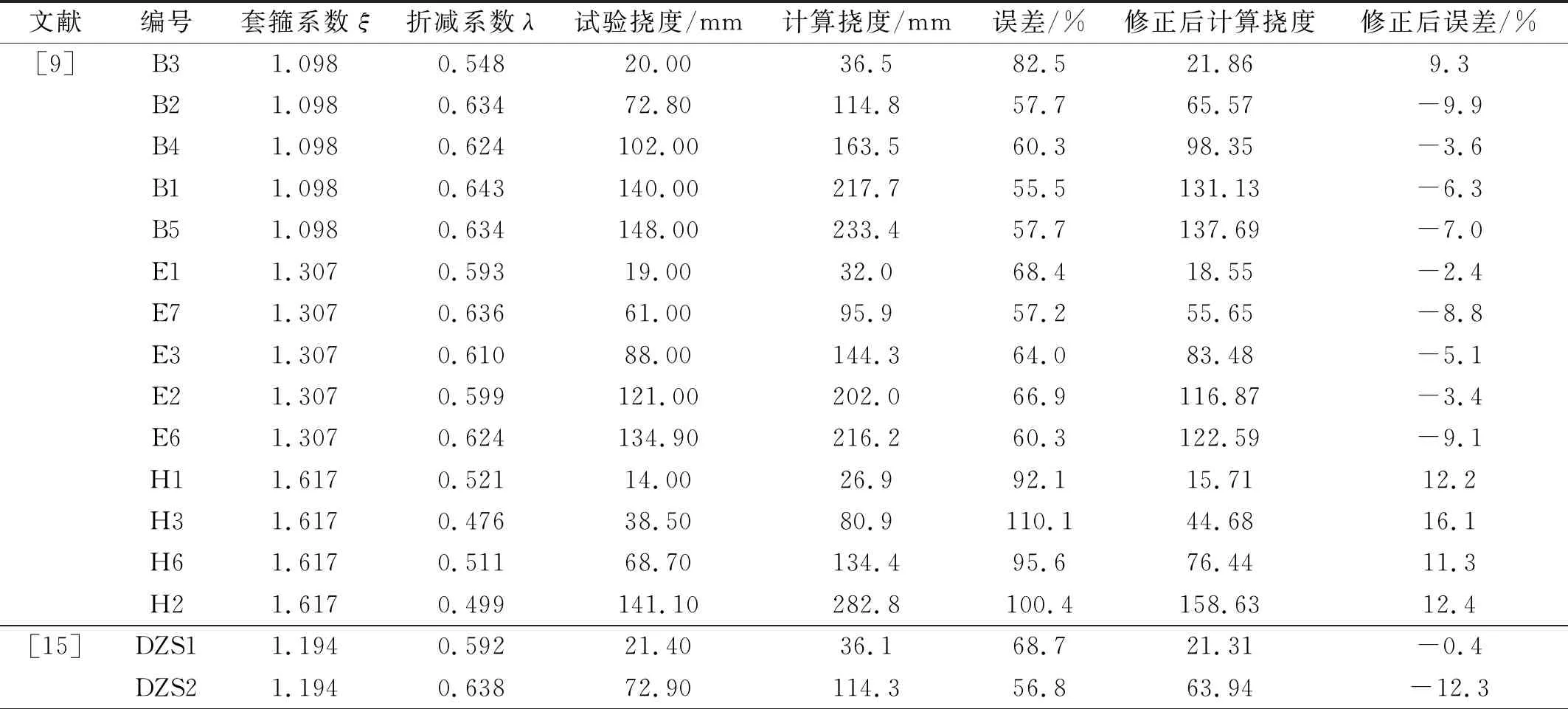
表3 两端简支边界条件构件挠度计算结果

表3(续)

表4 固简支边界条件构件挠度计算结果比较

表5 方差分析结果

λ=-0.158ξ2+0.199ξ+0.6

(26)

由图3可知，拟合优度R2为0.815，这表明统计回归模型有效的反映了折减系数与套箍系数之间的变化规律和发展趋势。其中，挠度修正计算公式的适用范围为：ξ=0.500～1.617。

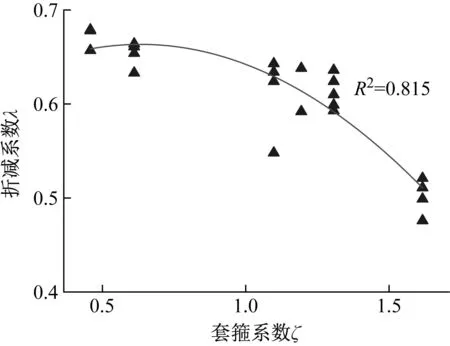
图3 两端简支边界条件下拟合图

2.3 一端固支、一端简支边界条件下挠度计算公式

同理，得到钢管混凝土固简支构件的冲击点挠度计算公式。表4统计了国内外11根固简支钢管混凝土冲击构件，由统计结果，折减系数λ与套箍系数ξ之间存在一个明显的线性函数关系，即

λ=-0.066ξ+0.656

(27)

由图4可知，拟合优度为0.829，这表明统计回归模型有效的反映了折减系数与套箍系数之间的变化规律和发展趋势。其中，挠度修正计算公式的适用范围为：ξ=0.500～1.307。

图4 两端固简支边界条件下拟合图

同时，为了保证构件在低速冲击下能够发生弯曲变形，并避免构件断裂，应该确定公式中的冲击质量和冲击速度的范围：m1=193.35～920.00 kg；v0=3.96～14.48 m/s。

3 公式的有限元验证

3.1 有限元模型的建立

通过挠度修正公式计算统计的样本挠度，误差减小到了20%以内(见表2～表4)。为了进一步验证其的计算精度，采用王路明等研究中YG1和YG4为原型拓展样本(具体参数见表1)，改变钢管厚度、冲击位置、冲击速度、冲击体质量等参数，建立模型。

采用LS-DYNA建立有限元模型，采用六面体网格进行单元划分。对于材料参数，混凝土采用LS-DYNA中072R3号材料(*MAT_CONCRETE_DAMAGE_ REL3)，通过定义应变率-增强系数曲线(横坐标为有效应变率，纵坐标为强度增强系数)来考虑混凝土的应变率效应。钢管采用LS-DYNA中003号材料(*MAT_PLASTIC_KINEMATIC)，钢材的屈服强度和应变率的关系采用Cowper Symonds应变速率模型中的应变速率参数C和P来体现。冲击体和支座均看作刚体，不考虑变形的影响，通过LS-DYNA中020号材料(*MAT_RIGID) 来模拟冲击体和支座，并固定支座的各个方向。通过关键字(*CONTACT_AUTOMATIC_SURFACE _TO_SURFACE)来模拟冲击体与构件之间的接触、冲击体和支座之间的接触，钢管单元和混凝土单元之间设置为共节点，不考虑钢管与混凝土之间的黏结滑移。

3.2 模拟可靠性验证

为了验证数值模拟所采用参数的准确性和精度，YG1和YG4的冲击时程曲线和位移时程曲线如图5所示。通过对比发现，两组构件的冲击力和位移时程曲线变化趋势基本一致。最大挠度、冲击力平台值、持续时间的误差如表6所示，均在合理范围内。综上所述，试验结果和仿真结果能够良好的吻合，模拟所采用的参数具有足够的准确性和精度。

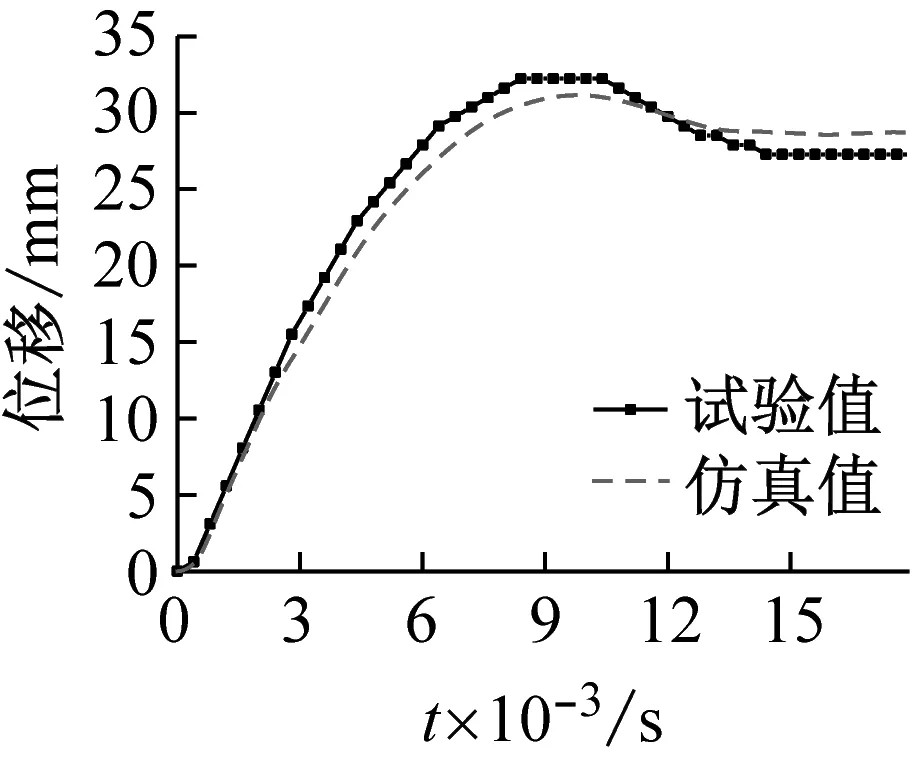
(a) YG1位移时程曲线

表6 仿真分析与试验结果对比

3.3 数值模拟对公式的验证

利用拓展样本YZ1～YZ10对公式进行验证，拓展样本的构件信息、数值模拟结果和挠度修正公式计算结果如表7所示。对于数值模拟下拓展样本的10根构件，修正公式计算挠度与数值模拟的挠度误差都在10%以内。综上可知，公式的计算精度良好，可以较好的预测钢管混凝土构件遭受横向冲击下的最大挠度。

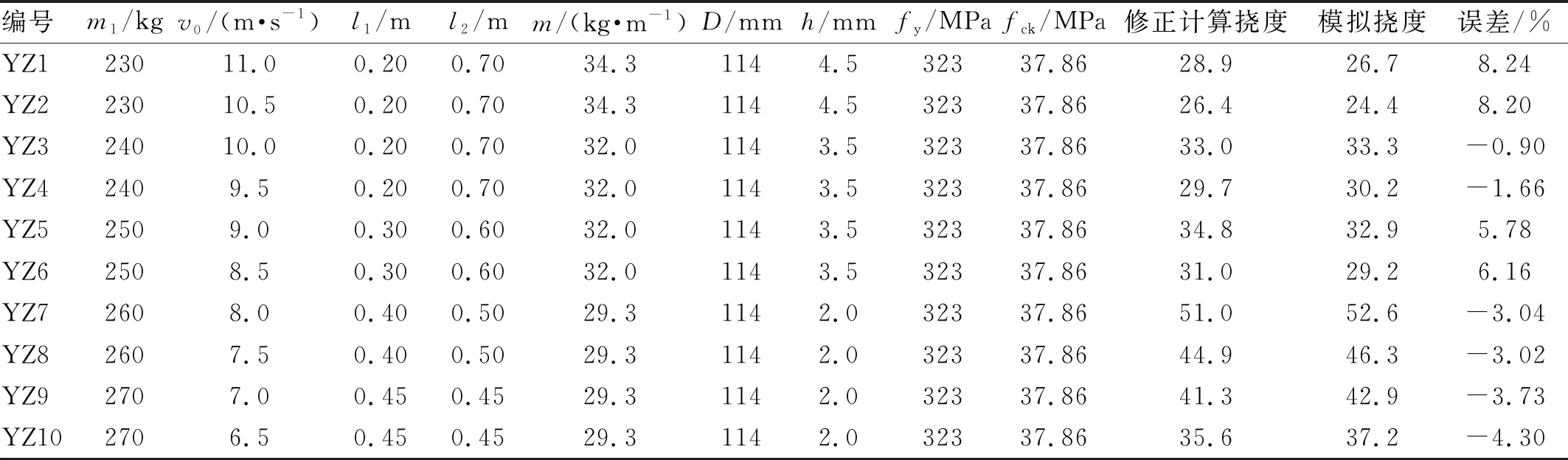
表7 数值模拟构件挠度计算结果比较

4 结 论

本文对任一横向冲击点、不同边界条件下的圆钢管混凝土构件最大挠度计算方法进行研究，得到以下结论：

(1) 基于移行铰理论和材料理想刚塑性假设，将圆钢管混凝土构件受到横向冲击作用下运动分为3个运动相，并进行了每一相的运动受力分析，计算出每一相的挠度值，得出了不同边界条件下构件的最大挠度理论计算公式。

(2) 通过比较试验挠度与计算挠度，发现挠度理论计算公式偏于保守，其原因为基于刚塑性假定的推导过程没有考虑能量损失和局部变形。

(3) 提出修正系数λ来修正理论公式，以弥补刚塑性假定的局限性。通过对55组试验样本方差分析，发现修正系数λ和套箍系数ξ显著相关。

(4) 针对套箍系数ξ对挠度计算误差进行修正，拟合得到修正系数λ的计算公式。并通过数值模拟拓展验证样本，对比发现挠度修正公式计算结果与数值模拟结果的误差保持在10%以内，验证了提出的挠度修正公式的准确性。

(5) 但上述研究方法折减系数仍然具有局限性：套箍系数虽然是折减系数高度显著因素，但折减系数仍可能与刚度、长细比等因素相关；且统计样本的尺寸偏小，需要补充实验进行进一步研究和验证。在后续的研究中将综合考虑与套箍系数、刚度、长细比等多因素的拟合关系，并综合考虑尺寸效应，以得到更为准确合理的结论。