动力吸振器在声黑洞单元中的放置位置对减振效果的影响

贾秀娴， 赵 剑， 杜 宇， 于 野

(大连理工大学 汽车工程学院,辽宁 大连 116024)

随着近些年来能源问题和环境问题的日益严重，为了降低运载工具的传统能源消耗以及减少污染排放，轻量化研究成为运载工具发展的必然趋势。然而，减轻结构质量，在一定程度上会恶化振动及噪声性能。因此，如何在轻量化的同时保持甚至提高减振降噪性能已成为汽车、高速列车、船舶以及航空航天运载工具的研究热点之一。一种基于声黑洞(acoustic black hole,ABH)理论的结构，其可以潜在地实现使用较少附加质量就可有效控制结构振动噪声响应，因此逐渐得到越来越多的关注和研究。

Pekeris[1]观察到，在分层、非均匀的媒质中，横截面的厚度线性衰减到0之后，声波并没有发生反射。Mironov[2]研究波在楔形体中传播时指出，当楔形体的截面轮廓变化符合一定指数规律时，即h(x)=εxm(其中ε为常数，m为正有理数，且m>2)，且当其厚度平滑地减小为0时，其内弯曲波传播到厚度为0的点(奇点)时，相速度趋于0，即波无法到达楔形板的末端，从而不会发生反射。基于这一效应，Krylov等[3-8]提出ABH的概念，并利用ABH效应对结构进行了一系列的减振研究。理论上，ABH结构可以吸收100%的入射波能量，并可应用于空气环境或者液体环境中的不同工程结构，同样也适用于使用Lamb波的超声波设备。然而任何实际结构都不可能存在0厚度，加工过程中的制造偏差、切割工具引起的卷曲以及过早的切断，使得实际存在的ABH结构边缘均具有一个具体的厚度，其反射能量可达50%～70%。研究表明，即使边缘厚度的存在、制造工艺不足够精准等缺陷会削弱ABH的聚焦效应，但ABH结构也能够被广泛地应用，起到减振降噪的有效作用。实际应用中的ABH结构截面轮廓变化规律为h(x)=εxm+hmin，其中hmin为ABH区域的最薄厚度，轮廓变化如图1所示。图1中h0为均匀厚度区域的厚度。

图1 声黑洞结构示意图

以周期性排列着ABH单元的变厚度板结构为主要研究对象，Conlon等[9-11]从声功率、损耗系数、模态损失因子、能量流在变厚度板结构中的分布、ABH单元的动态特性及参数设计等方面进行了研究，讨论了该结构的振动衰减效果。结果表明：周期性排列的ABH结构可以使辐射声功率减少高达20 dB。而且使用多个动力吸振器(dynamic vibration absorber，DVA)针对一个激励频率下的振动进行减振控制相对于单个DVA效果要好很多[12]。当分布式的动力吸振器应用在ABH单元周期性排列的变厚度板结构时，被证明在宽频带内有较好的减振效果。但是，由文献[13]可知，在某些频率下，将DVA放置在ABH结构的中心位置时减振效果并不明显。其原因可能是在实际模型中，ABH中心位置的厚度大于0，与基于等于0的理论假设不符，从而导致聚焦位置并不在ABH的中心。因此，将DVA放置在该位置的减振效果不符合理论预期。此外，在某些模态下，ABH的中央位置还有可能成为动态响应为零的点，这时将DVA放置在该位置时势必不会产生任何减振效果。因此，DVA放置位置对减振效果的影响至关重要，而根本原因是聚焦位置。

本文首先通过射线声学理论直观展示了不同入射角度下ABH结构的弯曲波聚焦路径，初步了解弯曲波在ABH结构中的传播路径和聚焦位置。其次，使用数值搜索法[14]确定多个DVA的参数。最后，通过有限元仿真计算对比分析两种DVA布置方案(即ABH单元中心位置和聚焦位置)的振动响应。

1 ABH结构的弯曲波聚焦位置

在ABH理论中，假设其中心位置厚度为0，其聚焦位置必然位于中心处。但实际物体中的ABH无法加工成0厚度(即hmin≠0)。因此，其聚焦位置可能不在中心处。通过使用射线声学理论，可以直接观察到嵌入ABH结构变厚度板中弯曲波的传播路径以及聚焦位置。本文分别探究了两种入射方式下的弯曲波聚焦位置，即中央点源激励和平面波激励。

1.1 数值模型参数

使用的ABH结构为半径R=100 mm的圆形，即x0=100 mm，如图2所示。由图1中的幂律轮廓以最薄点为中心旋转形成，4个同尺寸的ABH结构对称地嵌入在一块无限大的自由边界板中，相邻两个ABH结构的中心间距为d=204 mm。板的均匀厚度部分h0=8 mm，ABH区域最薄处(即圆心处)厚度为hmin=1 mm，厚度变化的幂指数设为m=2.2。板结构材料为钢，弹性模量E=196 GPa，密度ρ=7 850 kg/m3，泊松比v=0.3，假设无材料阻尼。从图2可知，板左侧箭头为平面波激励方向，位于板几何中心处三角形内的点代表点源激励位置。

图2 结构模型的示意图

1.2 射线声学

射线声学，即几何声学，类似于几何光学方法，声音以射线形式传播。在射线声学的范畴内，有两个基本的方程：一个是用于确定声线行走轨迹的程函方程；一个是用于确定单根声线强度的强度方程。这两个方程可以在一定的近似条件下得到。非耦合弹性波射线的运动轨迹方程[15]为

(1)

(2)

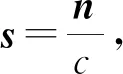
1.3 中央位置的点源激励

在不考虑反射波的情况下，使用MATLAB软件对式(1)和式(2)求解，得到弯曲波在ABH结构中的传播轨迹。变厚度板结构在30 kHz频率的中央点源激励下弯曲波传播的轨迹图，如图3所示。入射角从原点出发(见图2)，每隔6°增加一条入射线模拟点源激励。以板的几何中心(0，0)为原点，4个象限内相应于原点处点激励的响应关于几何中心对称，故取第一象限讨论。第一象限中ABH单元的几何中心坐标为(102 mm，102 mm)，图3中弯曲波在第一象限的聚焦位置为(125.98 mm，125.95 mm)，二者并不重合。

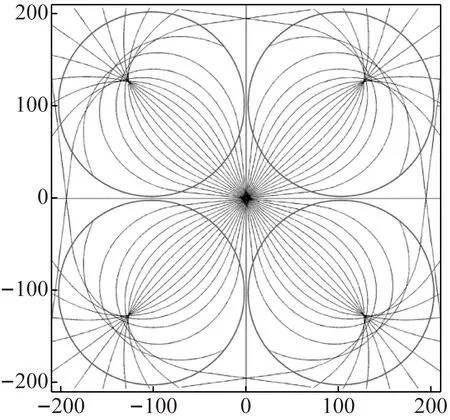
图3 30 kHz点激励条件下弯曲波的传播轨迹(mm)

1.4 边界位置的平面波激励

当平面波激励从板的一侧进入(见图2左端入射)，模型设入射角为0°，每隔5 mm增加一条入射线，共80条平行入射线。变厚度板结构在30 kHz平面波激励下弯曲波传播的轨迹图，如图4所示。以板中心为原点，图4显示在第一、第二象限的聚焦位置分别为(132 mm, 102 mm)和(-72 mm, 102 mm)。若以每个ABH单元的中心为原点分别建立坐标系，则弯曲波在这两个单元中相对于各自圆心的聚焦位置相同。此结论也同样适用于第三、第四象限。

图4 平面波激励条件下弯曲波传播轨迹(mm)

与点源激励仿真结果类似，当ABH结构的最薄处厚度不为0时，其对弯曲波产生的聚焦位置与ABH结构几何中心不重合。

2 DVA的位置对减振效果的影响

2.1 结构模型

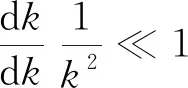
使用4个DVA对结构进行减振，每个ABH单元内布置一个DVA。由文献[13]以及第1章的研究结果可知，为了提高减振效果，当附加DVA时，ABH结构的中央位置(即厚度最薄处)并非最佳位置。本节利用有限元仿真的方法得到中央点源激励在3 677 Hz下ABH单元的聚焦位置，其在第一象限中的坐标为(130 mm, 130 mm)，而第一象限中ABH单元的几何中心位置为(102 mm,102 mm)。未加DVA的变厚度板(variable thickness plate,VTP)模型。根据放置位置的不同将附加DVA的模型分为两种:一种是将DVA放置在ABH单元的中心位置(VTP-DVA-Center)，以板中心为零点，整体结构为中心对称结构，DVA在第一象限的坐标为(102 mm, 102 mm);另外一种是放置在能量聚焦处(VTP-DVA-Focus)，DVA在第一象限的放置位置坐标为(130 mm, 130 mm)。

2.2 参数优化

DVA参数的优化目标是针对3 677 Hz激励条件下产生的共振峰进行优化，同时使得3 677 Hz附近一定带宽内(4个DVA中最小共振频率2 985 Hz，最大共振频率4 042 Hz)的响应得到较好的控制。假设板结构为无阻尼结构，DVA的刚度ki(i=1,2,…,6)保持一致，第i个DVA的固有频率、质量、阻尼分别为

(3)

(4)

ci=2miξTωi

(5)

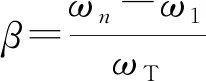
通过使用数值搜索技术，获得DVA的最优参数公式

(6)

(7)

(8)

DVA的总质量与板结构的质量比μ=0.1，当DVA的个数n=4时，计算得到调谐频带宽β=0.3，调谐频率比f=0.96，阻尼比率ξT=0.082。各个DVA的参数，如表1所示。

表1 DVA参数

2.3 加速度频率响应云图

通过使用Hypermesh有限元软件进行前后处理，板结构使用四面体单元进行网格细致划分，采用Nastran有限元分析软件进行求解计算(该有限元仿真方法的可靠性和精度已经在之前的研究工作中得到详细论证)。通过计算得到了垂直于板面方向的加速度频响云图，如图5所示。图5(a)为未加DVA时的加速度响应，图5(b)为将DVA附加在ABH结构中央位置的加速度响应，图5(c)为DVA放置在能量聚集位置处的加速度响应。模型VTP，VTP-DVA-Center,VTP-DVA-Focus在云图中的最大值分别为：2.34×107mm/s2，3.26×104mm/s2，8.63×103mm/s2。分析可知，加了DVA之后，最大值至少降低了57 dB。而且，将DVA放置在能量聚集位置比放置在ABH单元的中心位置衰减了11.5 dB。通过观察云图的色度区域可知，加了DVA之后，较大响应区域的面积是减小的，而且，VTP-DVA-Focus的较大值区域面积较前两种情况显著减少。

图5 3 677 Hz激励频率下的加速度响应云图

2.4 平均加速度频率响应对比

2.3节中板上所有节点的平均加速度在2 700～4 200 Hz频带内的频率响应曲线，如图6所示。第f个激励频率下的平均加速度响应值Af为

(9)

式中:f=1,2,…,m，m为激励频率的总个数;ai为第i个节点的加速度值，i=1,2,…,n;n为仿真模型中的总节点个数。

表2所示有3条曲线的各峰值。加了DVA之后，加速度平均响应的峰值得到较大幅度的抑制，第一个峰值降低了至少26.9 dB，第二个峰值降低了至少27.9 dB,如图6所示。而且，当将DVA放置在能量聚集位置处时，峰值减少为一个，另外，相对于VTP-DVA1模型在约3.8 kHz的峰值衰减了16.7 dB。

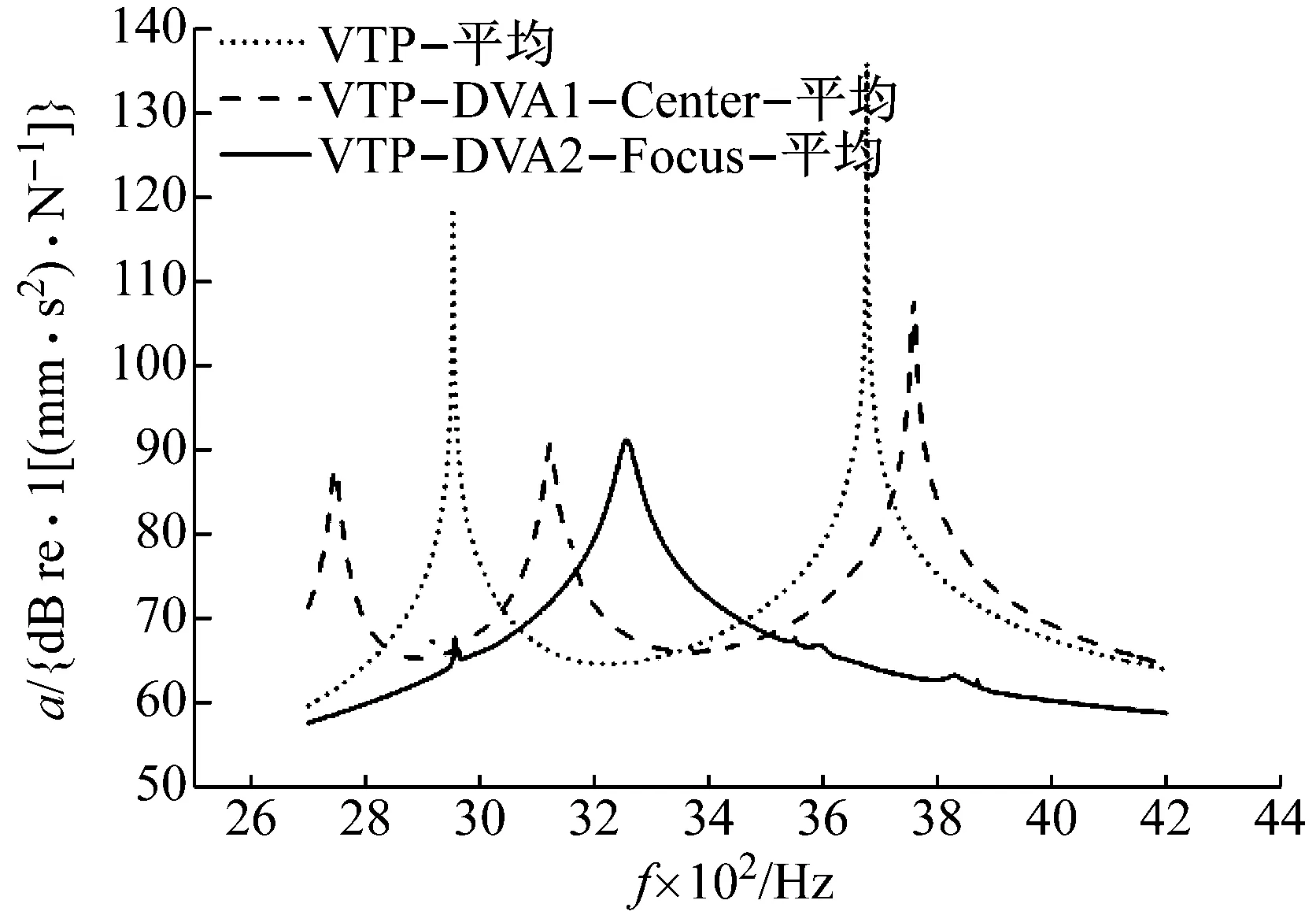
图6 板的平均加速度响应

表2 各板的总平均加速度值及平均加速度响应曲线的峰值

在2 700～4 200 Hz内，板的总平均加速度响应值Aw为

(10)

各板的总平均加速度值(见表2)。在频带内附加DVA后，加速度总平均响应明显降低。并且相比将DVA布置在ABH中心，放置在聚焦位置的总平均加速度值降低幅度更大。

3 结 论

本文以周期性排列的ABH结构为研究对象，使用多个DVA对一个频率进行振动控制。通过调整DVA的放置位置，使结构的振动衰减效果达到更高的水平。通过有限元仿真得到板结构的加速度响应的云图以及平均加速度响应曲线，探讨了DVA的放置位置对减振效果的影响。结论如下：

(1) 应用射线声学理论方法获得弯曲波传播的轨迹，观察到当ABH结构的最薄厚度不为0时，其聚焦位置没有出现在其几何中心位置。

(2) 对于3 677 Hz的共振频率，放置在能量聚焦处的DVA结构能够更有效地衰减板的平均加速度响应峰值，与放置在ABH单元中心位置相比，其最大峰值衰减了16.7 dB，同时峰值的数量由3个减少为一个。

(3) 通过对比总体平均加速度，可知附加DVA在2 700～4 200 Hz内具有明显的振动衰减效果，尤其是当把DVA放置在ABH聚焦位置时，总平均加速度值降低了28 dB。比DVA在中心位置时衰减了9.2 dB，明显优于放置在ABH中心处。