向量值亚纯函数修正的亏量和
2021-10-18李琛,赵静
李 琛,赵 静
(商丘师范学院 数学与统计学院,河南 商丘 476000)
引言
20世纪20年代初,芬兰数学家R.Nevanlinna[1]引进了亚纯函数的特征函数并以此建立了Nevanlinna理论(即复平面上的亚纯函数值分布理论).它是复分析理论研究的重要工具,也是二十世纪最伟大的数学成就之一.近百年来, Nevanlinna理论不断发展,并广泛应用于亚纯函数唯一性理论研究等各个方面.它不仅奠定了现代亚纯函数理论的基础,也对其他许多数学分支的交叉和融合产生了重要的影响.上世纪末,著名数学家E.Picard和E.Borel先后获得了比较突出的研究成果.在这之后,很多学者从事这方面的研究,因而逐渐形成了整函数与亚纯函数值分布理论.
Nevanlinna理论不断发展.其中一个重要的方面是引进了导数,通常把导数与函数本身结合起来考虑值分布问题.起初是建立相应的结果,例如Milloux不等式、熊庆来不等式、Miranda定则等.之后则进一步考虑引进导数后特有的问题,例如庄圻泰关于亚纯函数与其导数的特征函数的比较、Hayman不等式以及最近顾永兴获得的正规定则等[2-7].涉及亏量和的亚纯函数的值分布理论问题是近年来复分析专家关注的热点课题[8-10].
本文中如未进行特殊说明, 所涉及到的亚纯函数均是指在开复平面C上.
C={z:|z|<∞}
扩充复平面表示为:
1 预备知识
为了方便,我们先介绍一些基本的概念和符号.

设f(z)是定义在CR={|z| 假设读者熟悉Nevanlinna理论的基本概念和结果及其标准记号[11-13],例如m(r,f),T(r,f),m(r,a),T(r,a),S(r,f),等等. Toda在1970年给出如下定义. 定义1[14]如果α表示任意小于ρ的非负数(ρ>0)(特别地,当ρ=0时,α=0).对任意正数r0,记: 这里ψ(t)是关于T(r,f)的辅助函数. 结合Nevanlinna理论中的相关定义记号,得到推广的相关记号如下. 定义2[15]设f(z)是在|z|<∞上的亚纯函数,记: 其中Tα(r,r0,f)叫做关于f(z)推广的α特征函数. P.K.Jain在R.Nevanlinna对亏量的定义的基础上,对其定义做出进一步推广并给出推广的亏量定义如下. Tα(r,f)=mα(r,f)+Nα(r,f)=mα(r,a)+Nα(r,a)+ε(r) 在定义3中,结合上述推广的第一基本定理可得到如下定义. 定义4设f(z)是在|z|<∞上的亚纯函数,对任意复数a,记: 为了证明本文中的结论,我们先引入以下几个引理. 引理1[16]如果f(z)是超越的向量值亚纯函数,对任意的α,有: 引理2[16]如果f(z)是超越的向量值亚纯函数,对任意的α,有: 证明令 其中: mα(r,Ff′)+(l-1)Sα(r,f) 本文在推广的亏量定义的基础上,把亏量的定义从亚纯函数推广到向量值亚纯函数上,并给出了向量值亚纯函数修正的亏量和的一个不等式结论,下面是定理内容及相关证明. 定理2如果f(z)是在E上的超越的向量值亚纯函数,则对任意的整数l有: 证明令ai(i=1,2,…)是无穷序列C上的不同元素,则对任意a∈C,δα(a,f)>0有: (1) 令q>2,由引理3得: 令q→∞,结合式(1)式可得: 左半不等式得证,下面证明右半不等式. 得: 进一步变形可得: 右半不等式得证. 本文在Nevanlinna基本理论的基础上对亚纯函数及向量值亚纯函数的亏量定义进行了推广,得到推广的亏量形式.并将亚纯函数亏量和的相关结论推广到向量值亚纯函数上,给出了向量值亚纯函数修正的亏量和的一个结论并给出了相关证明过程.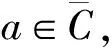
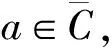
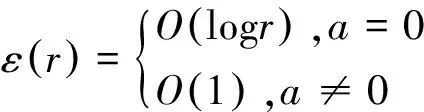
2 相关引理及证明




3 定理及证明


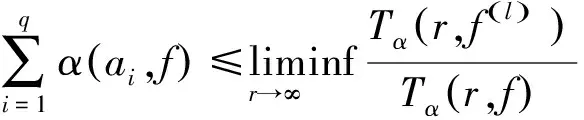

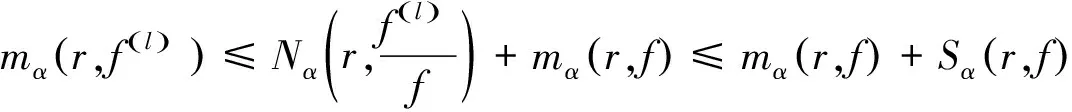
4 结语
