基于二维微流控模型的多孔介质渗透特性
2021-10-18陈超聂绍凯刘鹏飞陈云敏巴特
陈超,聂绍凯,刘鹏飞,陈云敏,巴特
(1.浙江大学岩土工程研究所,浙江杭州,310058;2.浙江大学软弱土与环境土工教育部重点实验室,浙江杭州,310058)
多孔介质材料的渗透特性引起了很多学者的研究兴趣。岩土体作为一种典型的多孔介质材料,其内部渗透特性对于坝体等工程的稳定性[1]、污染场地修复[2]、天然气水合物开采[3]等有重要的指导意义。影响多孔介质内流体输送和渗透特性最主要的因素有孔隙率、孔隙连接方式、孔隙曲折度和多孔介质的比表面积等[4−5]。
对于多孔介质材料渗透特性的预测最早由KOZENY 开展,通过一系列等长度和直径的平行毛细管模型计算流体流动时多孔介质两端的压降,进而分析多孔介质的渗透系数,CARMAN对该方法进行了修正,得到了较合理的Kozeny-Carman公式(KC 公式)[6−7]。在此之后,不断地有学者对该公式进行了修正和补充[8−11]。
传统上对于多孔介质内部流动规律的研究多基于宏观模型,比如土柱试验和箱型模型试验等[12−13]。OVALLE-VILLAMI 等[12]利用离心机研究了岩土体中孔隙特性和离心加速度对于流动特性的影响,分析了超重力下达西定律和福希海默定律的适用性。近年来,GUO等[14−16]也使用简化的微观模型,采用理论推导和数值模拟的方法进行研究;AKBARI等[17]使用微模型研究了流体流进矩形通道后的压力变化,并与理论解相比较,发现两者能较好地符合;YANG 等[18]提出了一种分析模型,预测各向同性、完全饱和的微开孔金属泡沫的渗透特性;REN 等[19]从理论分析、基于有限元的数值模拟、实验室试验和现场试验4个方面回顾了水合沉积物渗透性的测量和估算方法。3D 打印技术也被用来构建模型研究多孔介质的渗透特性。PIOVESAN 等[20]使用高分辨率的CT 图像提取了材料的三维孔隙结构,采用聚甲基丙烯酸甲酯(PMMA)打印出多孔结构来研究其渗透性,并通过数值模拟进行建模,发现提取的孔隙结构和建模参数对渗透特性有很大的影响。
传统三维模型无法观察多孔介质内部的结构和细观变化,因此,利用简化的二维模型研究多孔介质的渗透特性也是很多学者的研究方向。JOSEPH等[21]对原位的储层岩心取样扫描,提取岩心的孔隙结构,构建二维裂隙通道模型,发现岩心渗透率随多孔介质的孔隙和喉道数量增加而明显上升;SCHOLZ等[22]利用观测多孔介质内部的粒子流动特性来测量多孔介质的渗透系数。然而,简易二维微观尺度的模型试验有其局限性,通过多孔介质两端的压力变化来计算渗透系数也存在一定偏差。KOSAR 等[23]采用低长宽比的微模型探究层流条件下的压降和摩擦因数,发现宏观条件下试验结果不能预测微观的试验结果;GUNDA等[4]在低雷诺数下测量带有集成微柱的微通道两端的压降和流阻,通过达西方程计算出模型的渗透系数。但试验结果和理论值存在一定偏差,这是因为作者对通道两端的压降进行了修正和简化。
微流控作为一项新兴的技术,最早被应用在化学和生物学领域[24]。随着微纳加工技术的进步,更多的人使用微流控模型模拟多孔介质的流体流动[25]:如多孔介质内部不混溶流体的相互驱替[26],细颗粒在多孔介质内部的迁移和堵塞效应等[27]。渗透性是表征多孔介质特性的重要参数,反映了流体流进多孔介质的难易程度。使用微流控模型来研究多孔介质的渗透性是一个很好的方法。
本文作者利用微流控技术制作出二维多孔介质芯片,测量芯片两端的压降并进行修正,结合芯片孔隙参数,利用KC公式及其修正公式,研究多孔介质渗透系数和其内部结构的关系。
1 试验设计
1.1 微流控芯片
通过软光刻技术制作二维聚二甲基硅氧烷(PDMS)微流控芯片(长×宽为2 cm×1 cm)。
首先,使用硅片制作微流控芯片模具,设计的图案代表简化的二维多孔介质模型;
然后,将液态的PDMS倒在模具上;
最后,待其固化和硬化后,使用氧等离子体处理PDMS和玻璃片并将二者键合[28]。
研究中使用的所有芯片的微柱高度均为50 μm。芯片图案是中心对称的。每个芯片都有一个入口和一个出口,入口和出口具有二叉树状结构,旨在确保芯片内部形成均匀的流场(图1)。本次试验共设计3组芯片,C1组和C2组芯片的微柱直径分别为200 μm 和500 μm,但微柱排列方式分别为正方形和正三角形;C3组芯片微柱为正三角形排列,微柱直径均为250 μm,孔喉直径为40~60 μm(表1)。
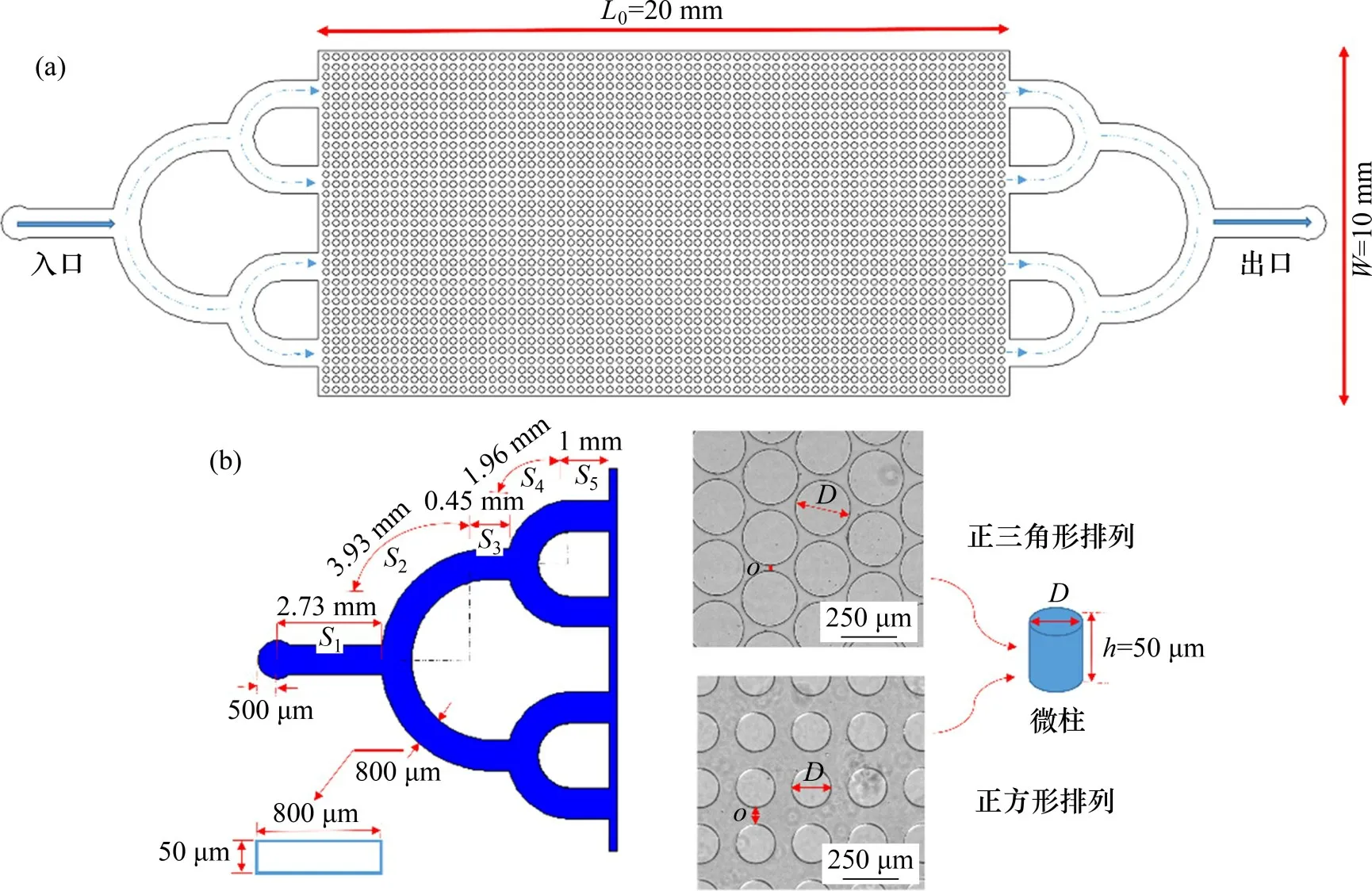
图1 微流控芯片结构示意图Fig.1 Schematic diagram of microfluidic chips structure
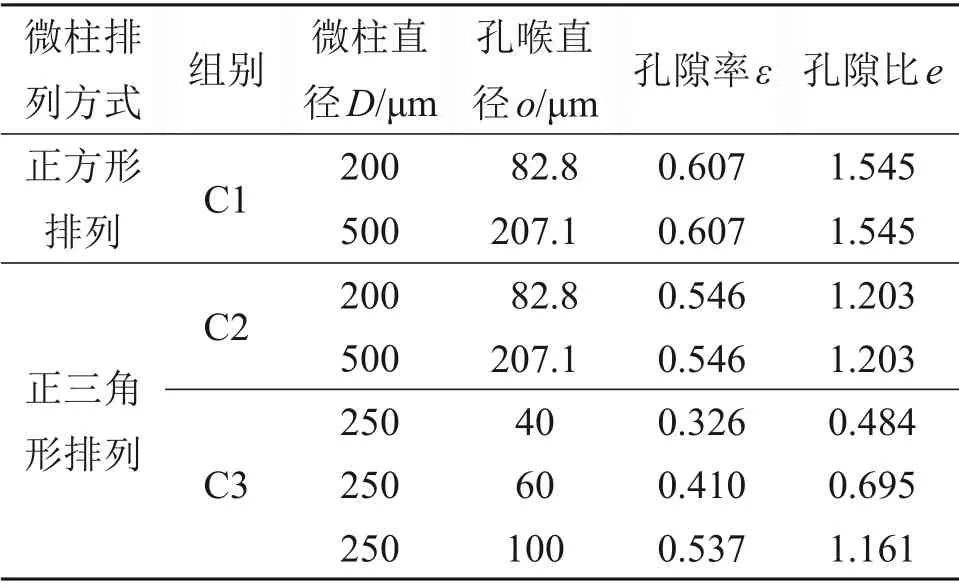
表1 设计芯片类型及内部结构参数Table 1 Sizes of micropillars and pore throats
1.2 试验设备
研究微流控芯片渗透性能的试验装置如图2所示。本次试验使用无气去离子水作为输送流体,用精密注射泵(PHD ULTRA 4400,Harvard Apparatus,US)将无气水注入到微流控芯片中,该注射泵可以提供恒定且无脉冲的流量。微流控芯片和注射泵之间通过毛细管和钢针连接。

图2 测量压降的试验装置图Fig.2 Schematic of experimental facility used for pressure drop measurements
在芯片的入口和出口处,2 个压力传感器(uPS01-T116,LabSmith,美国)的测量范围为−100~150 kPa,配合数据采集软件,监测芯片两端的压力变化。此外,配置1 台倒置显微镜(Ti 2,Nikon Corp,日本),内置高速CCD 相机(Zyla 4.0,Andor Technology,Belfast,英国),观测芯片内部的情况,确保在整个试验过程中芯片内部没有气泡。
1.3 试验步骤
首先,制作无气水。将去离子水放入真空抽气机中抽气30 min,排除水中的气体,避免去离子水中的气体影响。
其次,按照图1所示的方法连接装置,并将压力传感器调零,以较高流量(1 mL/min)通入无气水,利用PDMS 材料微小的透气性排除掉芯片内部残余的气泡,使芯片内部完全饱和。
最后,通过倒置显微镜观察芯片内部的流动情况,至芯片内部饱和后开始记录数据。
本次试验设计的流量范围为0.1~4.0 mL/min,由于压力传感器的量程为−100~150 kPa,在孔隙率较低的芯片中未能达到4.0 mL/min,当压力达到传感器量程时,试验暂停。在每次调整输入流量后,应保证压力传感器显示的压力稳定后再进行记录,记录的压力时间为3 min,以其平均值作为测量点的压力。整个试验过程在室温下(约25 ℃)进行。
2 试验结果
雷诺数Re计算公式为

式中:ρ为流体密度;v为流速;D为特征长度,本试验中取微柱的直径;μ为流体黏度。本次试验条件下的雷诺数0 在低雷诺数条件下,水力梯度与流速呈线性关系,流动由黏滞力控制,可以用达西渗透公式表示: 式中:ΔP为压降;L为多孔介质的长度;g为重力加速度;k为渗透系数。 在高雷诺数条件下,流动由黏滞力和惯性力共同控制,水力梯度与流速呈非线性关系,可以用福希海默公式表示: 式中:A和B为福希海默系数。 在整个流动体系中,由于压力测量点并未严格意义位于多孔介质两端,因此,应该对所测量的压降ΔP进行修正[17]。 式中:ΔPm为实测压降;ΔPt为入口和出口管道的压降;ΔPc为芯片内部入口和出口通道的压降;ΔPa为直角转弯处和管道中截面变化产生的压降;ΔPe为电黏滞效应产生的压降。 首先,对于ΔPc,以宽矩形断面的Poiseuille流动为基础,对于横截面宽度远大于高度的矩形来说,通道压降可通过以下方程得出[12,29]: 式中:d为圆管直径。 结合式(5)和式(6),可以得出式(7),计算矩形通达内的压降。 式中:L0为流道的长度;f为摩擦因数;Dp为流道的等效直径。 由图1可知:在整个芯片的两端,通道的长度L0已在图1中标出,流道的宽度w为0.8 mm,流道的高度h为50 μm。由此可以计算出ΔPc。 对于ΔPt,可直接根据圆形管道中的阻力计算: 式中:L1为圆管流道的长度(单侧1 cm);这里d取0.8 mm。 对于直角转弯处和管道中截面变化产生的压降ΔPm,由文献[17]中公式得到: 式中:Q为流量;A为矩形通道截面积;At为圆管通道截面积;Kc,Ke和Kb为损失系数,取1.2,经过计算其数值可以忽略。 当流体在有压力的狭窄通道中流动时,流体与壁面因为双电层的影响会产生压降ΔPe,其与壁面材料和流体的种类有关。在以PDMS 作为壁面材料,水作为流动介质的情况下,此压降也可以忽略[17]。 图3所示为不同尺寸和微柱排列方式的芯片在注入无气去离子水过程中单位长度的压降和流阻与注入流量之间的变化关系。由图3(a)可见:在低流量阶段(<1 mL/min),正方形排列和正三角形排列(C2)的芯片两端的压降和流量呈较好线性关系;在高流量阶段(>1 mL/min)时,这种线性关系消失,压降增长速率也逐渐降低,可能是在高流量条件下的PDMS材料的变形引发[30]。 图3 微柱不同直径和排列方式芯片的压降与流阻随流量的变化规律Fig.3 Variation of pressure drops and flow resistance in microfluidic chips with different flow rates and micropillar diameters and arrangements 在这2种排列方式中,相同流量条件下,正三角形排列(C2)比正方形排列表现出更大压降。正三角形排列(C2)中流体流经的距离更长,流线更复杂,在芯片内部受到的阻力也更大,因此压降也更大。在同一种排列方式中,孔喉直径较小的芯片比孔喉直径更大的芯片表现出更大压降,正方形排列和正三角形排列(C2)均表现出这种现象。值得注意的是,本次设计的微流控芯片组内的孔隙率相同(表1),但是在不同的流量条件下表现出不同的压降变化。 流动阻力R又称摩擦阻力,是黏性流体在运动过程中产生的阻碍流动的反作用力。 由图3(b)可见:流阻随着流量Q增大而减小,且逐渐趋于稳定;在流量相同的条件下,正三角形排列(C2)芯片的流阻大于正方形排列的流阻;在同种排列方式内,较小孔喉尺寸也反映出更大流动阻力,这与前文分析结果一致。 KC公式为预测多孔介质材料渗透系数的半经验公式,在地下水渗流和油气开采等多个领域被广泛使用,其表达式如下: 式中:K为渗透率;γp为流体的容重;k0为形状系数;T为孔隙流道的曲折度;S0为多孔介质材料单位体积的表面积。 自从Kozeny-Carman公式提出后,学者们不断地对其进行修正,提出了很多估算多孔材料渗透率的计算公式,如表2所示。但前人们的研究多使用实验室尺度的土柱和箱型模型来进行试验,未能在微观尺度上设置孔隙结构来探究渗透系数形成的原因。本次试验使用微流控芯片制作的二维孔隙结构来探索渗透系数与孔隙率之间的联系。 表2 不同学者对Kozeny-Carman方程进行的修正Table 2 Correction of Kozeny-Carman equation by different scholars 试验中使用正三角形排列C3 组的芯片进行渗透试验,分析芯片渗透系数与芯片结构的关系,芯片参数如表1所示。试验的流量范围为0.025~1.000 mL/min,根据前文可知,当Q<1 mL/min时,芯片两端的压降和流量呈较好线性关系。因此,可根据达西定律(式(2))计算芯片的渗透系数。利用测得的压降,经过修正绘制出C3 组芯片的流速v和水力梯度i的关系,如图4所示。 图4 C3组芯片流速v和水力梯度i的关系Fig.4 Relationship between flow velocity v and flow gradient i 经线性拟合,得出图4中C3组v−i图线的拟合直线斜率,即渗透系数分别为1.04×10−4,1.28×10−4和1.82×10−4m/s。用经典的KC 公式(式(10),其中k0T2即KC 常数。多孔介质芯片的渗透系数如表3所示。 表3 C3组芯片试验和理论推导的渗透系数Table 3 Permeability coefficients of C3 derived from experiments in this study and theories of previous scholars m/s 通过试验测得压差计算的渗透系数与用经典KC公式计算得到的渗透系数十分接近。因此,可以利用经典的KC公式预测微流控芯片等均匀多孔介质的渗透系数。然而,对于非均匀多孔介质的渗透系数还有待进一步研究。 1)多孔介质材料的内部结构决定其渗透特性,不同的孔隙结构具有不同渗透特性。 2)微柱为正方形排列的芯片在流动过程中比正三角形排列(C2)的芯片具有更小压降和流动阻力。 3)在同种排列形式中,孔喉直径也影响渗透特性。孔喉直径越大,渗流过程中也具有更小的压降和流动阻力。 4)试验测得的微流控芯片的渗透系数与由KC公式计算到的渗透系数较接近。因此,利用经典的KC公式可以较准确地估算均匀多孔介质的渗透系数。 5)由于PDMS 材料本身具有一定的弹性,在试验过程中,芯片内部的孔隙在一定的流量和压力条件下会发生形变,进而在影响试验中测得的压力。接下来将采用玻璃材质的孔隙结构进行试验。
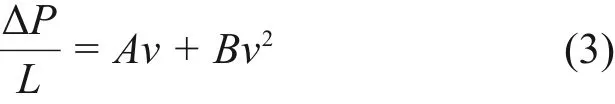
2.1 压降分析



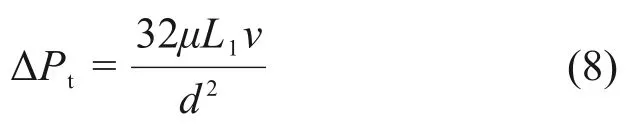


2.2 流阻分析

3 渗透系数分析
3.1 KC公式预测渗透系数
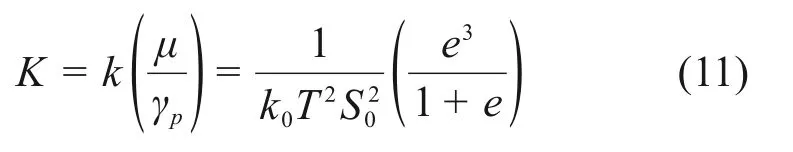

3.2 微流控芯片的渗透系数


4 结论
