晶粒组织对7B04铝合金超塑性变形机理的影响

2021-10-18陈锦廖荣跃孙泉刘晓东叶凌英

中南大学学报（自然科学版） 2021年9期

陈锦，廖荣跃，孙泉，刘晓东，叶凌英

(1.中南大学材料科学与工程学院，湖南长沙，410083；2.中南大学有色金属材料科学与工程教育部重点实验室，湖南长沙，410083)

超塑性指细晶金属材料在一定变形温度、应变速率等条件下，可达到很大的的伸长率，且变形过程中流变应力很小、无明显颈缩的现象[1−2]。这种现象最早由PEARSON[3]在Sn-37%Pb 和Bi-44%Sn 共晶合金的挤压材料的慢速拉伸实验中发现，其中Bi-44%Sn 共晶合金的伸长率达到了1 950%。随后，BACKOFEN[4]利用超塑性成形零部件。该技术在复杂形状产品制造中的优势引起了国内外众多研究者的兴趣和重视，如Superform公司每年利用超塑成形技术生产数十万件产品[5]。尽管在过去的几十年里，关于超塑性变形时的应变速率、应力、晶粒粒径和温度等重要参数的研究众多，但对于超塑性变形机理的物理科学本质认识进展不大[6]。

目前普遍认为可以利用晶界滑移、扩散蠕变及晶内位错滑移这3种变形机理的协调机制来解释超塑性变形行为[7−8]。对于超塑性变形过程中以何种机制为主，仍存在争议，即使在对同种合金材料的研究中，也存在着不同的超塑性变形机制。如对于Al-Mg-Mn 合金，YAKOVTSEVA 等[9]发现其主要的变形机制为晶内位错滑移协调的扩散蠕变机制，晶界滑移贡献量很小；MIKHAYLOVSKAYA等[10]也发现在Al-Mg-Mn 合金的超塑性变形过程中晶界滑移所做出的贡献很小；而MASUDA 等[11]则指出Al-Mg-Mn合金的拉伸超塑性由伴随着刚性晶粒旋转和晶粒滑动的晶界滑移所导致，与之前关于Al-Mg-Mn合金的研究结论相反。

在7B04 铝合金超塑性变形过程中，也存在着不尽相同的结论。王建等[12]利用变形激活能发现7B04 细晶铝合金的超塑性变形为晶格扩散控制；而廖荣跃等[13]利用聚焦离子束(focused ion beams，FIB)刻蚀定量分析发现7B04 铝合金超塑性变形过程中伴随着扩散蠕变的晶界滑移机制。引起上述问题的可能原因是不同的研究中使用材料晶粒组织存在差异，对变形机制存在影响。本文作者利用FIB[6,14]在2 种不同晶粒组织的7B04 铝合金板材上刻蚀微米尺寸网格，在相同变形条件下拉伸后，通过变形前后的网格变化定量计算晶内位错滑移、晶界滑移和扩散蠕变对总变形的贡献量，从而分析晶粒组织对7B04 铝合金的超塑性变形机理的影响。

1 实验材料及方法

1.1 实验材料

实验材料为初始厚度为12 mm 的7B04 铝合金板材，该合金板材的化学成分如表1所示。

表1 7B04铝合金板材的化学成分(质量分数)Table 1 Chemical composition of 7B04 aluminum alloy sheet(mass fraction) %

1.2 实验方法

首先，将12 mm 厚的7B04 铝合金板材经485 ℃/4 h固溶后水淬，随后进行400 ℃/8 h 过时效处理，在200 ℃下进行多道次轧制得到2 mm厚的铝合金板材。将该2 mm 厚的板材在480 ℃进行30 min 的盐浴再结晶退火，使得晶粒细化得到细晶板材，并在细晶板材基础上经530 ℃/48 h 空气炉退火得到粗晶板材。

将所制得的细晶和粗晶板材沿其轧制方向制成如图1所示的标准试样[8]，用于超塑性高温拉伸。超塑性高温拉伸在对开式三段电阻丝加热炉加热的RWS50 高温拉伸试验机上进行，温度波动范围为±5 ℃。变形条件采用廖荣跃等[13]所获得的变形温度为515 ℃和初始应变速率为5×10−4s−1的7B04的最适宜变形条件。

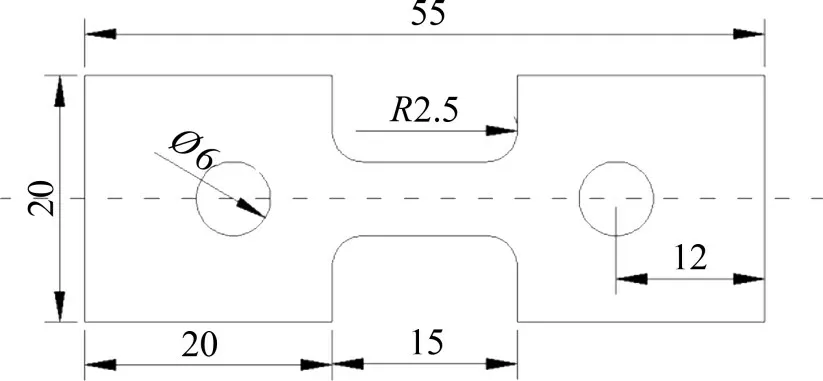
图1 超塑性拉伸试样形状和尺寸[8]Fig.1 Superplastic tensile specimen shape and size

1)将2 种试样进行120 ℃/12 h 时效处理(为保持一致性，后续所用试样进行此处理)，并进行金相组织观察。

2)在上述变形条件下拉伸至断裂，分析其力学特征，并利用速度突变法得到应变速率敏感性指数。

3)对2种原有试样在高温拉伸前进行FIB刻蚀处理，处理过程如下：抛光后用混合酸(1% HF+3% CrO3+16% HNO3+83% H2O，体积分数)腐蚀，进行高温拉伸之前，在Helios Nanolab 600i 双束电子显微镜下，利用F IB在拉伸试样标距段内约1/2处刻划10 条平行于拉伸轴的刻痕线，并在此处刻划10 条垂直于拉伸轴的刻痕线，刻线深度均为0.8 μm，线间距为50 μm，形成一个10×10 的闭合大网格。在大网格附近取线宽为0.5 μm，线间距为3 μm，分别刻划20 条平行于拉伸轴的刻痕线及20 条垂直于此刻痕线的刻线，使之形成闭合小网格[10]。

4)对刻蚀后的2种试样在相同变形条件下拉伸至不同真应变时停止，利用扫描电镜及透射电镜观察其晶粒、网格及其他微观组织演变。

5)根据变形前后网格的变化定量计算位错滑移及晶界滑移对总体变形的贡献量[15]，间接得到扩散蠕变的贡献量，从而分析各变形机理对超塑性总体变形的影响，并对比分析细晶和粗晶板材超塑性变形的区别。

2 实验结果

2.1 变形前显微组织

图2所示为2种不同晶粒组织板材的三维金相图。由图2可见：细晶板材沿轧向晶粒粒径较小，晶粒形状多为等轴状。而粗晶板材中轧向上晶粒粒径比细晶板材的大，且多为长条状晶粒，并含有许多细小的晶粒分布于大晶粒周围。在2种板材的轧面上，晶粒都大致保持等轴状。表2所示为2种7B04 铝合金板材纵截面上的平均晶粒粒径和晶粒纵横比统计结果，得到细晶和粗晶的平均粒径分别为9.7 μm 和11.8 μm。细晶板材纵横比较小，为1.89，而粗晶板材的纵横比略大于细晶板材的纵横比，为2.39。

表2 2种7B04铝合金板材的晶粒粒径及晶粒纵横比统计表Table 2 Grain size and aspect ratio statistics of two kinds of 7B04 aluminum alloy plates

图2 2种7B04铝合金板材三维金相组织Fig.2 Three-dimensional metallographic structure of two kinds of 7B04 aluminum alloy plates

2.2 应力−应变特征

图3所示是细晶和粗晶板材在变形温度为515 ℃和初始应变速率为5×10−4s−1的适宜变形条件下拉伸至断裂的真应力−真应变曲线。细晶板材的伸长率为1 180%，其峰值应力为6.9 MPa，而粗晶板材的伸长率为690%，其峰值应力为6.0 MPa。因此，细晶板材的流动应力随真应变增加首先呈现急剧增加的趋势，后逐渐变缓，到变形后期，呈现明显软化趋势，应力随着真应变增加而下降，直至断裂。而粗晶板材在初始变形阶段，流动应力随着真应变增加而明显增大，达到峰值应力后，应力缓慢下降趋于平缓，直至断裂。

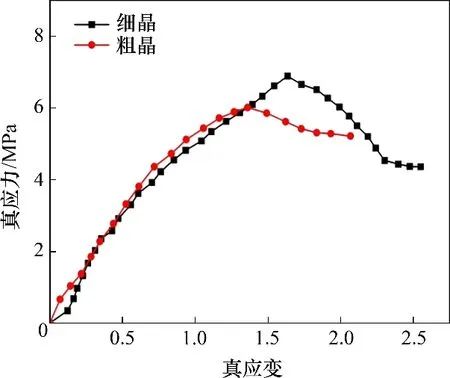
图3 7B04铝合金在适宜变形条件下的真应力−真应变曲线Fig.3 True stress−true strain curve of 7B04 aluminum alloy under suitable deformation conditions

图4所示为2 种板材在该变形条件下的载荷−真应变曲线及其对应的应变速率敏感性指数−真应变曲线。材料的应变速率敏感性指数m反映金属在变形过程中抵抗颈缩的能力，可利用速度突变法[16]求得。

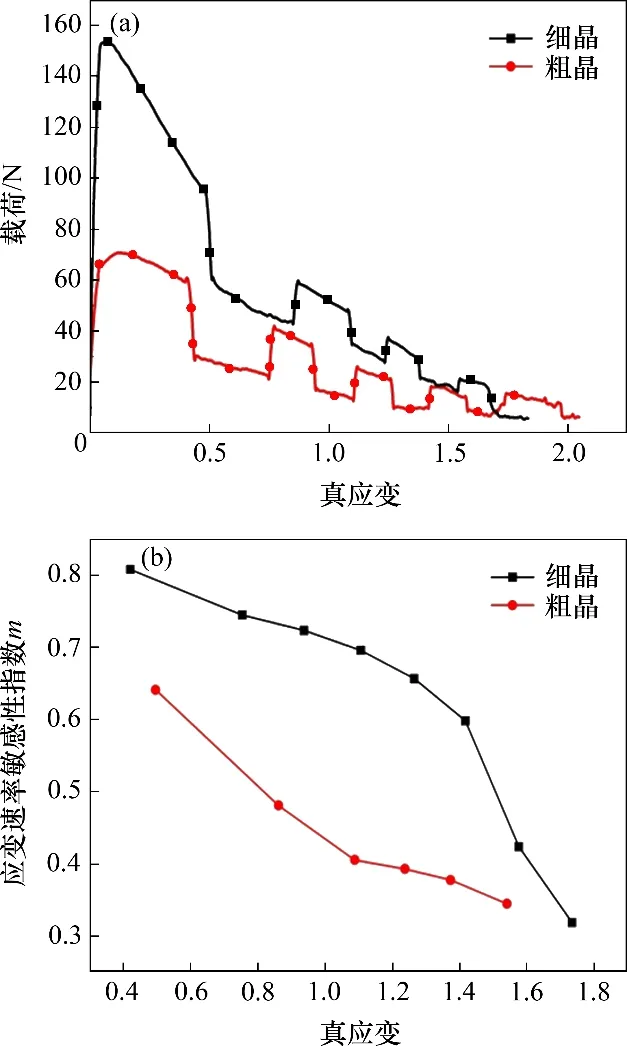
图4 2种样品的载荷−真应变曲线及对应的应变速率敏感性指数变化曲线Fig.4 Load−true strain curve and corresponding strain rate sensitivity index change curve of two samples

先以v1为5×10−3mm/s 的恒定夹头移动速度进行拉伸，待流动稳定后将夹头速度突升至v2为1×10−2mm/s，这时拉伸载荷会跃至一点，此处的载荷记作PA，拉伸过程中交替改变拉伸速度，得到如图4所示的载荷−应变曲线。利用外推法可得到不改变夹头速度时与该点具有相同应变所对应的载荷PB，并利用下式求得应变速率敏感性指数m：

一般认为，当m大于0.3 时，材料具有超塑性，而当m大于0.5时，材料的超塑性变形机理主要为晶界滑移[17]。由应变速率敏感型指数−真应变曲线可知，2 种板材的m整体分布在0.30～0.85 之间，且随着真应变增大，m减小，说明7B04 铝合金在本实验条件下具有超塑性。

对于细晶板材来说，其m随真应变增加时变化范围较大，而粗晶板材随真应变改变的变化幅度较小。在同一真应变下，细晶板材的m大于粗晶板材的m。结合2种板材在5×10−4s−1的初始应变速率条件下的伸长率可大致得到：细晶板材在该变形条件下，m较大，故超塑性变形能力更强，伸长率更大。

3 超塑性变形机理

3.1 晶内位错滑移机制的贡献

图5和图6所示分别为细晶和粗晶板材拉伸至不同真应变时的表面细网格的形貌变化。整体上来看，在拉伸过程中整个细网格沿拉伸方向伸长，而垂直于拉伸方向的部分收缩。细晶板材随着变形开始，晶界开始显现，晶粒开始出现高低起伏现象，这说明在拉应力的作用下，部分晶粒出现错动。随着真应变增加，细晶板材沿拉伸方向晶界处的网格发生明显错动，而垂直于拉伸方向的晶界处网格出现条纹带扩展，但晶内网格未发生明显变形，部分被晶界处条纹带扩展所覆盖。直至真应变增大至1.03 时，部分晶内网格仍保持原始形貌，而条纹带扩展覆盖了大部分网格。而粗晶板材相较于细晶板材，其条纹带扩展较少，大部分网格形貌保留完整，晶内处网格未发生错动和明显变形。在整个变形过程中，晶粒内部的网格线未发生明显变化，说明晶粒内部未发生变形。随着真应变增加，晶界处的网格发生错动，且逐渐被变形过程中不断扩展的条纹带所掩盖。

图5 细晶板材拉伸至不同真应变下表面细网格的形貌变化Fig.5 Morphology of fine mesh on surface of fine-grained sheets stretched to different true strains

对比图5和图6可见：相较于粗晶板材来说，细晶板材的条纹带扩展更长。由于晶内位错滑移一般会导致等轴晶粒沿拉伸方向明显长大[18]，因此，利用变形前后晶粒内部细网格长宽比的变化可以定量计算晶内位错滑移对整个超塑性变形的贡献量。2种板材在超塑性变形过程中，晶粒内部的小网格未发生明显变形，主要为晶界处的变形，说明等轴晶粒内部未沿拉伸方向发生变形，晶内位错滑移未对2种板材的超塑性变形产生贡献，即细晶和粗晶中晶内位错滑移对总体变形的贡献量接近0。

3.2 晶界滑移机制的贡献

利用FIB刻蚀得到的试样拉伸后表面10×10的粗网格形貌变化如图7所示。当板材发生超塑性变形时，经过晶界处的网格线会产生偏移，且随着变形量增加，其偏移量增大，因此可以利用所刻网格线在晶界处的平均偏移量来计算晶界滑移机制对7B04 铝合金板材总体变形的贡献量。其计算方法[15]如下：

图7 板材拉伸前后表面粗网格的形貌变化Fig.7 Morphology of coarse grid on surface of sheet before and after stretching

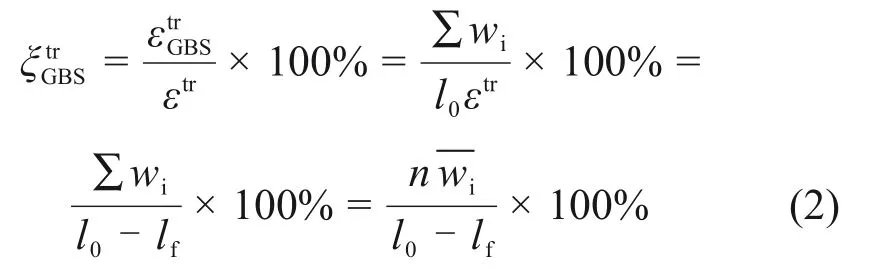
式中：为晶界滑移对样品变形的贡献比例；εtr为板材的总变形量；为晶界滑移变形量；wi为晶界处网格线条的偏移量；为晶界处网格线条的平均偏移量；n为轴向单位长度上的晶粒数；l0为变形前垂直于轴向的刻痕线的平均长度；lf为变形后刻痕线的长度。

表3和表4分别统计了细晶和粗晶板材的各超塑性变形机制对样品变形的贡献比例。根据表3和表4可知：随着细晶板材变形量增加，其晶界滑移的贡献量呈增加趋势；当真应变为0.16 时，晶界滑移贡献量为40.32%；当真应变增大至0.43 时，所对应的贡献量为52.34%；而粗晶板材的晶界滑移贡献量随变形量增加而降低，从真应变为0.15时的95.65%减小至真应变为0.41时的65.94%。

表4 粗晶板材中各变形机制对总变形的贡献Table 4 Contribution of various deformation mechanisms to total deformation of coarse-grained sheets

根据表面细网格的分析可知，细晶板材和粗晶板材中晶内位错滑移机制的贡献量为0，则可相应得出2种板材中扩散蠕变机制的贡献量。扩散蠕变机制在细晶板材中对总体变形的贡献量随着真应变增加而减少，而在粗晶板材中则随着真应变增加而增加。在2种板材的变形初始阶段中，粗晶板材的晶界滑移对于总变形的贡献量比细晶板材的大，且随着真应变改变，贡献变化量更大，这说明细晶板材中变形较均匀、稳定。结合金相组织可知，粗晶板材中晶粒纵横比较大，且存在较多小晶粒，其晶界数量较多，变形过程中利于依靠晶界滑移来达到宏观变形。随着变形进行，粗晶板材中小晶粒晶界不断偏移、扩展，形成大晶粒，晶界数量减少，从而导致晶界滑移的贡献量降低。

对比表格中2种板材间接得到扩散蠕变的贡献量发现，粗晶板材的扩散蠕变贡献量低于细晶板材的扩散蠕变贡献量，根据表面晶粒形貌演变可知，粗晶板材在超塑性变形过程中由于扩散蠕变引起的垂直于拉伸方向的条纹带扩展较小，这也表明粗晶板材中扩散蠕变的贡献量较少。

3.3 扩散蠕变机制

扩散蠕变机制以空位扩散为基础[8]，在超塑性变形过程中，横向晶界即垂直于拉伸方向的晶界处形成空位，从而该处空位浓度较高，纵向晶界处空位浓度较低，在浓度梯度差的作用下，空位往纵向晶界附近迁移，形成无沉淀析出带，物质则在横向晶界处沉积[19]。细晶板材和粗晶板材在适宜变形条件下拉伸至真应变为0.53 时，晶界附近的无沉淀析出带如图8所示。细晶板材和粗晶板材经过超塑性变形拉伸后，都在纵向晶界处形成了一定程度的物质贫瘠区，即无沉淀析出带，且所形成的无沉淀析出带主要分布在晶界其中一侧，并非以晶界对称分布，这说明晶界处发生的扩散是不均匀的。当真应变相同时，细晶板材的无沉淀析出带宽于粗晶板材的无沉淀析出带，这说明拉伸至该应变时，扩散蠕变机制对于细晶板材的总体变形的贡献大于粗晶板材的总体变形的贡献。

图8 板材变形至真应变为0.53时晶界附近的无沉淀析出带形貌Fig.8 Morphology of no precipitation zone near grain boundary when ε is 0.53

根据将板材拉伸至不同真应变时所形成的无沉淀析出带宽度可以定量计算出扩散蠕变的贡献量，如表5和表6所示。计算方法[16]如下：

表5 细晶板材中扩散蠕变对总变形贡献量Table 5 Contribution of diffusion creep to totaldeformation of fine-grained sheets

表6 粗晶板材中扩散蠕变对总变形贡献量Table 6 Contribution of diffusion creep to total deformation of coarse-grained sheets

式中：为扩散蠕变对样品变形的贡献比例；为扩散蠕变的变形量；B为无沉淀析出带宽度；Bˉ为无沉淀析出带的平均宽度；n为轴向单位长度上的晶粒数。

当真应变为0.21 时，细晶板材中扩散蠕变的贡献量为54.82%，随着真应变增加至0.79，扩散蠕变的贡献量减小到5.95%，在真应变为1.22时贡献量增加至53.22%，真应变继续增加至1.50 时贡献量减小至16.78%，处于波动趋势。因此，在超塑性拉伸过程中，细晶板材中可能存在动态再结晶，导致无沉淀析出带周围的晶粒碎化成为再结晶晶核，从而导致无沉淀析出带的宽度和数量有所降低。随着变形量增加，晶粒长大，无沉淀析出带变宽，扩散蠕变贡献量增加。

粗晶板材超塑性变形过程中随着真应变从0.22增加至1.26，扩散蠕变贡献量呈增长趋势，从最小的8.43%增大至59.88%。这说明粗晶板材没有发生再结晶过程。随着变形增加，物质在横向晶界处沉积，而纵向晶界处的无沉淀析出带宽度不断增加。对比通过晶界滑移和晶内位错滑移间接得到的扩散蠕变的贡献量，发现利用无沉淀析出带宽度所计算的贡献量较小，这是由于部分第二相粒子向晶界附近靠拢，导致所测得的无沉淀析出带宽度较小。

4 晶粒迁移机制

在7B04 铝合金板材的高温拉伸过程中，应变速率敏感性指数m均大于0.3，断裂时细晶板材伸长率达1 180%，粗晶板材伸长率为690%，均表现出超塑性。

细晶板材的超塑性变形初始阶段，m高于0.5，说明此阶段该板材抗颈缩能力强，变形均匀。由表3可知：在真应变低于0.29时，细晶板材晶界滑移的贡献量略低于扩散蠕变的贡献量，说明在细晶板材的超塑性变形初始阶段，扩散蠕变机制为主导机制，伴随着晶界滑移机制。随着真应变增大，晶界滑移的贡献量增加，逐渐占据主导。这是由于在变形初始阶段，晶界滑移缓慢启动，变形初期主要为晶界扩散，随后转为晶界滑移。

在细晶板材的超塑性变形过程中观察到典型的扩散蠕变协调晶界滑移的Ashby-Verrall晶粒换位过程，如图9所示。将未变形的细晶板材的相邻4个晶粒分别标记为A，B，C 和D，如图9(a)所示，其中A和C晶粒相邻，将B和D晶粒分隔开来。由图9(b)可见：当真应变为0.43时，A和C晶粒的晶界通过变形所形成的条纹带相连，B和D晶粒相互靠拢。由图9(c)可见：随着真应变增至0.72，B 和D 晶粒继续靠拢，A 和C 晶粒被分隔开来。由图9(d)可见：继续变形至真应变为1.02时，A和C晶粒与相邻的B和D晶粒间的条纹带扩展，形成韧带组织，C晶粒破碎。结合表5可知，细晶板材的超塑性变形后期阶段，主要变形机理晶界滑移机制，扩散蠕变作为协调机制。

图9 细晶板材中Ashby-Verrall晶粒换位过程Fig.9 Ashby-Verrall grain transposition process in fine-grained plates

粗晶板材整体m比细晶板材的低，在变形初始阶段，m较大，变形均匀。由表4可知：粗晶板材超塑性变形过程中晶界滑移的贡献量高达95.65%，且随真应变增加而减小，结合m数据，可知在粗晶板材的超塑性变形初始阶段，以晶界滑移机制为主导，伴随着扩散蠕变的机制。粗晶板材中存在一定数量的小晶粒，变形时优先在这些小晶粒晶界处发生晶界滑移，随着变形不断加强，小晶粒逐渐迁移到大晶粒中间，该过程如图10所示。

图10所示为粗晶板材中小晶粒迁移换位过程，由图10可见：将未变形的粗晶板材的相邻3 个晶粒分别标记为D，E 和F，其中E 晶粒较小，与D和F 晶粒相接触。由图10(b)和10(c)可见：在超塑性拉伸过程中，E晶粒向D和F晶粒中间迁移，将D和F晶粒分隔开来，且D和F晶粒沿拉伸方向伸长，直至D，E 和F 沿拉伸方向排列成直线，如图10(d)所示。根据表6中粗晶板材无沉淀析出带宽度所得到的扩散蠕变贡献量可知，在超塑性变形的后期阶段，扩散蠕变机制占据主导地位。