CT 图像重建算法对比研究

彭 慧，孙维昆，冀东江

（天津职业技术师范大学理学院，天津 300222）

CT 图像重建是指通过对物体进行不同角度的射线扫描，根据检测到的数据来重建物体内部截面图像的技术[1]。目前主要的图像重建算法有2 类，分别为解析类重建算法和迭代类重建算法[2]。解析重建算法的特点为算法简单，计算量小，重建速度快，但在投影数据不完备或投影数据噪声大的情况下，获得的图像效果并不好[2]。解析重建算法中最常用的是滤波反投影算法（FBP）[3]。目前运用较多的迭代类重建算法有代数重建算法（ART）和联合代数重建算法（SART）[4]，该类算法可以获得较好的重建图像，但是耗时比较长[5]。ART 算法是由Gordon 等[6]于1970 年提出，该算法在低剂量重建时不能很好地起到去噪的作用，但是相比于FBP，其重建出来的图像更好。SART 算法是由Anderson 等[7]于1984 年提出，该算法在ART 的基础上进行了改进，可以解决ART 算法受噪声影响的问题，但是由于该算法不具备高速收敛性，进行一次图像更新需要所有的投影数据，所以在重建效率上比ART 算法低。Sidky 等[8]提出了基于最小化图像总变差的优化准则的迭代重建算法（TV），TV 模型可以很好地保持图像的边界，对于分片常数的图像重建效果很好，但是该算法常会在分片光滑区城产生“阶梯效应”。SART-TV 算法是一种基于最小化总变差，结合SART的重建算法。本文分别从稀疏角度和有限角度情况下，采用上述几种算法对Shepp-Logan 模型进行仿真试验，并比较其重建效果。

1 算法介绍及图像数值评价指标

1.1 FBP算法

FBP 算法的基本思想[9-10]：扫描被测物体，先把获得的投影函数做滤波处理，得到修正的投影函数，再对修正后的投影函数进行反投影，最后得到重建图像。FBP 算法的实现步骤：①在角度θ 下对原图像进行扫描，得到投影数据f（s，θ）。②求投影数据f（s，θ）的傅里叶变换，得到f（ω，θ），用滤波器的传递函数|ω|对f（ω，θ）进行滤波，得到Q（ω，θ）。③求Q（ω，θ）的以ω 为变量的一维傅里叶逆变换，得到q（ω，θ）。④用滤波后的数据q（ω，θ）进行反投影得到重建图像f（x，y）[10-11]。

1.2 ART算法

ART 算法的基本思想[10，12-13]：求解方程p=Au，其中u=[u1，u2，…，uN]T为待估计的图像，p=[p1，p2，…，pM]T为系统采集的真实投影数据，A 为系统矩阵，其维度为M×N。

ART 算法的公式

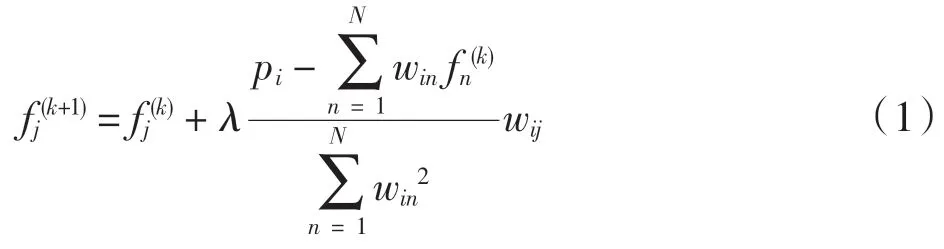
式中：0 <λ<1 为松弛因子；k 为迭代次数；N 为图像的大小；i 为第i 条射线；j 为第j 个像素点；fj(k)为第j个像素点的灰度值；pi为第i 条射线的真实投影数据；wij为第i 条射线与第j 个像素相交的长度[10，12，14]。

ART 算法的实现步骤[10，12，14]：①为被重建对象赋初值，给定ART 的迭代次数，松弛因子fj(k)=0，k=0，（j=1，2，…，N）。②计算估计投影值（i=1，…，M）。③计算由②得到的估计投影值和实际投影值的误差④利用误差对所有射线经过的像素点进行修正。⑤将上面的结果作为第一步的初始值，重复所有步骤，直到满足收敛条件或者达到迭代次数。

1.3 SART算法

SART 算法的基本思想[10，14]：在修正某个像素值前，需要计算经过像素的所有射线的误差来对该像素进行修正，并进行加权及归一化处理之后，再把上述结果更新到该像素上去，重复上述过程，直到满足收敛条件或迭代次数满足人为约定的值。

SART 算法的公式

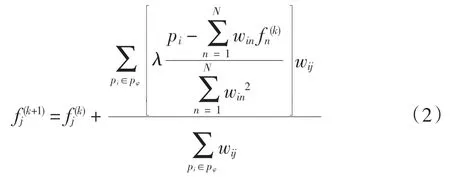
式中：pi为第条射线的实际投影数据；pφ为同一投影角度下的实际投影数据集合为理论投影值；λ为松弛因子[10，14]。

SART 算法的实现步骤：①为待重建对象赋初值，给定SART 的迭代次数，松弛因子fj(k)=0，k=0（j=1，2，…，N）。②计算理论投影值（i=1，…，M）。③计算由②得到的理论投影值与实际投影值的误差④对其余射线，重复上述步骤，计算其余射线的误差值。⑤用步骤④得到的所有射线误差值修正待重建图像，直到满足收敛条件或者迭代次数满足人为约定的值[10，14]。

1.4 SART-TV算法

SART-TV 算法的基本思想：基于TV 正则化，结合SART 算法。图像的TV 表示为[13-15]

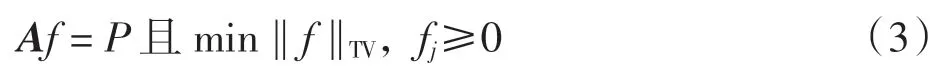
式中：f 为图像函数，其中每一个像素由fj，j=1，2，…，N 表示；P 为系统采集的真实投影数据；A 矩阵为射线穿过图像时和每一像素相交的长度的集合。要得到图像的总变差最小，要求图像总变差的梯度递减。图像像素对应的梯度定义为[13-15]

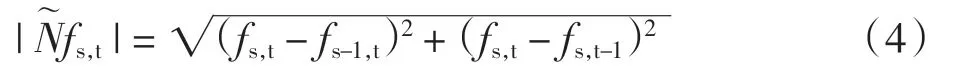
于是，图像的总变差（TV）写成下列形式

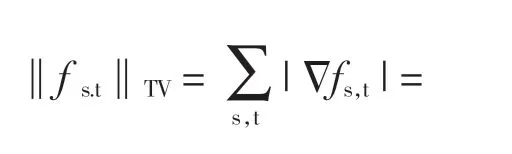
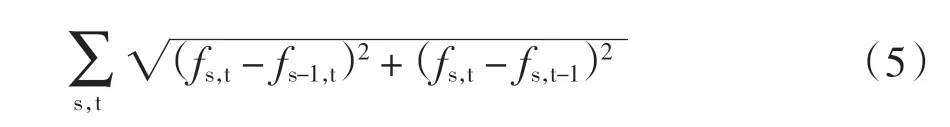
式中：fs，t为二维图像第s 行，第t 列像素的灰度值[14-16]。

SART-TV 重建算法步骤：①输入原始数据P，姿SART，kSART，KTV，for i=1：k，重建结果图像。②用式（2）计算SART，得到fi。③用式（5）对fi进行TV 正则化约束。④输出结果图像。

1.5 图像数值评价指标

本文分别采用均方误差（MSE）、峰值信噪比（PSNR）[17]来评价图像质量。

式中：ti，j、ri，j分别为原始图像和重建图像在像素（i，j）处的像素值；M×N 为图像的大小；MAX1为原图的最大像素值。

2 实验结果及分析

本文对Shepp-Logan 头模型进行图像重建仿真模拟，用Matlab R2018b 软件在PC 机（4.0 GB 内存，3.10 GHz CPU）上实现。重建物体的大小为256×256，一个扫描角度下探测元个数设置为256 个。

2.1 稀疏角度投影数据重建结果比较

本研究在180°范围内依次等间隔取样45 个投影和60 个投影，用FBP、ART、SART、SART-TV 4 种算法重建图像。在ART 算法中，kART=17，姿ART=0.2；在SART 算法中，kSART=5，姿SART=0.3；在SART-TV 算法中，kSART=10，姿SART=0.1，kTV=25。图1 和图2 分别为45 个、60 个投影情况下重建出的图像。

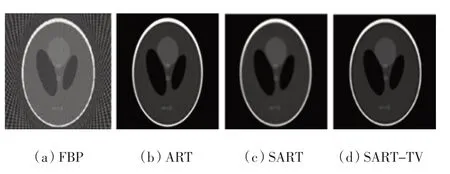
图1 45 个投影角度下重建结果

图2 60 个投影角度下重建结果

从主观角度来看，ART、SART、SART-TV 算法重建出的图像质量优于FBP。因为这3 种迭代算法重建出的图像只有较少的伪影，而FBP 算法重建出的图像伪影较重。为了客观分析不同算法重建图像的质量，本文计算了2 种评价图像质量的数值指标，如表1所示。

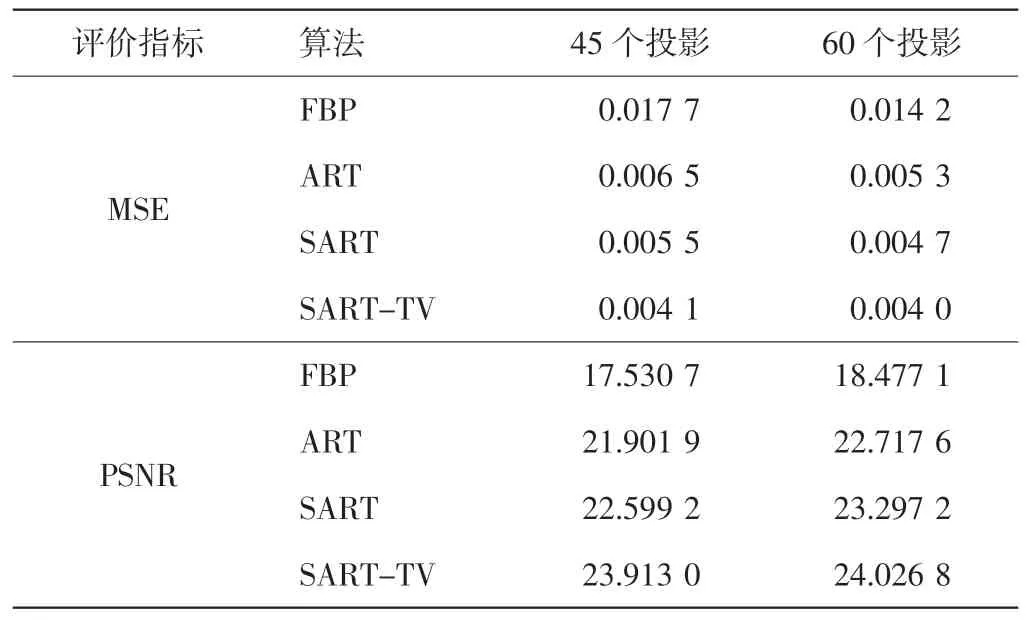
表1 4 种算法在2 种稀疏角度下的客观评价指标

由表1 可以看出，ART、SART、SART-TV 算法的均方误差小，峰值信噪比大，重建出的图像要好于FBP 算法。随着投影数据的增多，4 种算法的均方误差逐渐变小，峰值信噪比逐渐增大。由此可见，在稀疏采样的情况下，利用ART、SART、SART-TV 算法重建图像比较合适，相比之下SART-TV 重建结果更好。

图3 和图4 分别为45 个、60 个投影角度下每种迭代算法随着迭代次数增加时MSE 的结果。

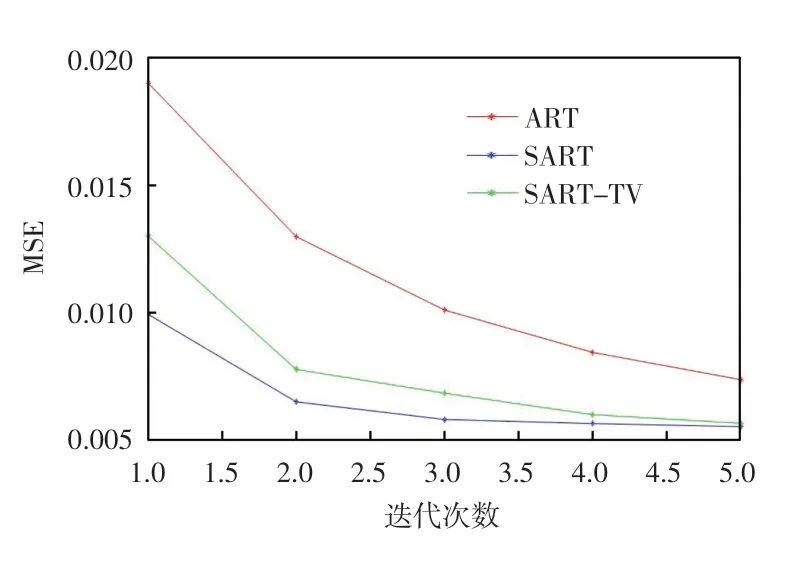
图3 45 个投影角度下MSE 结果

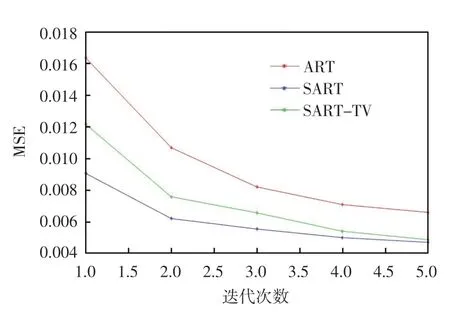
图4 60 个投影角度下MSE 结果

从图3、图4 中可以看出，随着迭代次数的增多，3种算法的均方误差逐渐减小，且逐渐趋于稳定，所以这3 种迭代算法是收敛的。并且在60 个稀疏投影下，每种算法的均方误差都比45 个稀疏投影情况下均方误差小。

2.2 有限角度投影数据重建结果比较

本文在[0°，130°]、[0°，150°]以及[0°，170°]范围内，每隔1°均匀采样，采用FBP、ART、SART、SART-TV 算法进行图像重建。在ART 算法中，kART=17，姿ART=0.2；在SART 算法中，kSART=5，姿SART=0.3；在SART-TV 算法中，kSART=10，姿SART=0.1，kTV=25。

有限角度的重建结果如图5 所示。从图5 可以看出，FBP 算法重建出的图像条状伪影较多，其他算法虽然也有伪影，但是比FBP 的更少。用FBP 算法进行重建时图像的细节恢复程度也没有迭代类算法的恢复程度好，并且获得的重建图像的效果从好到差依次为：SART-TV、SART、ART、FBP。随着角度的增多，4种算法重建出的图像逐渐变好，获得的图像数据越多，重建出来的图像也越接近原始图像。4 种算法在不同有限角下的客观评价指标如表2 所示。

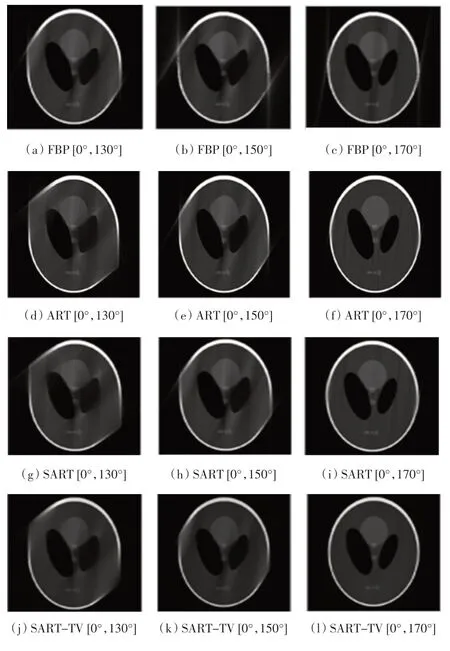
图5 有限角度的重建结果

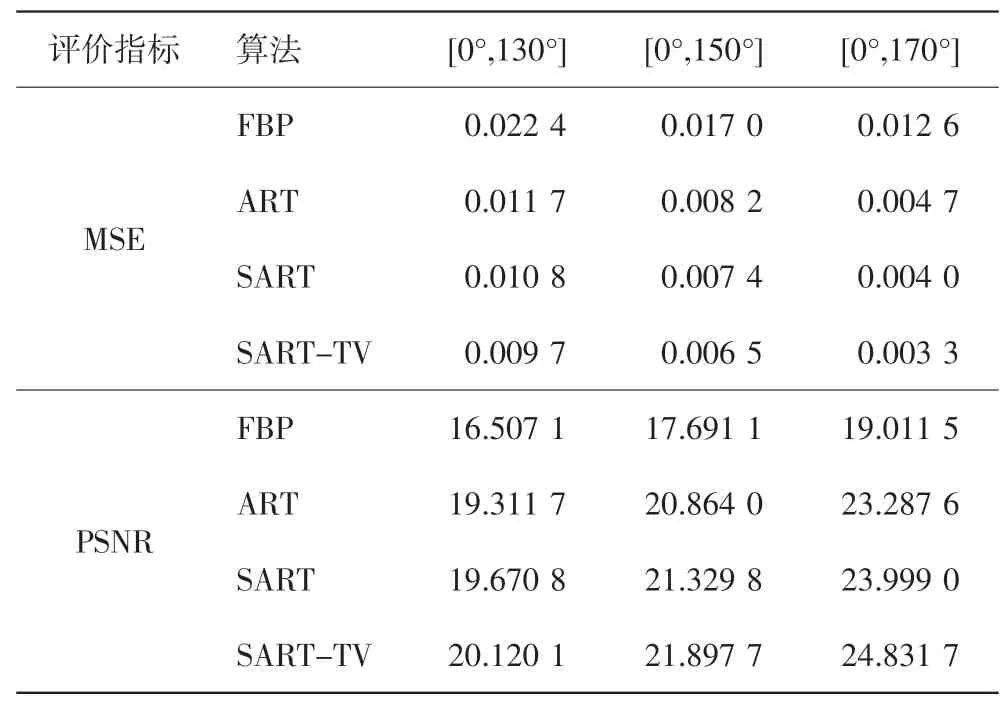
表2 4 种算法在不同有限角下的客观评价指标

从表2 可以看出，ART、SART、SART-TV 算法的均方误差小，峰值信噪比大，FBP 的均方误差比其他3种算法大，峰值信噪比比其他3 种算法小，相比之下SART-TV 算法的均方误差最小，峰值信噪比最大。所以，在有限角度的情况下，相比其他3 种算法，使用SART-TV 重建得到的图像更好。

在[0°，130°]、[0°，150°]、[0°，170°]下每种迭代算法随着迭代次数增加时MSE 的结果如图6—图8所示。从图6—图8 中可以看出，随着角度的增大，每种算法的MSE 都是减小的，同时随着迭代次数的增多，3 种算法的均方误差逐渐减小，且逐渐趋于稳定。于是，在有限角度情况下，这3 种迭代算法是收敛的。

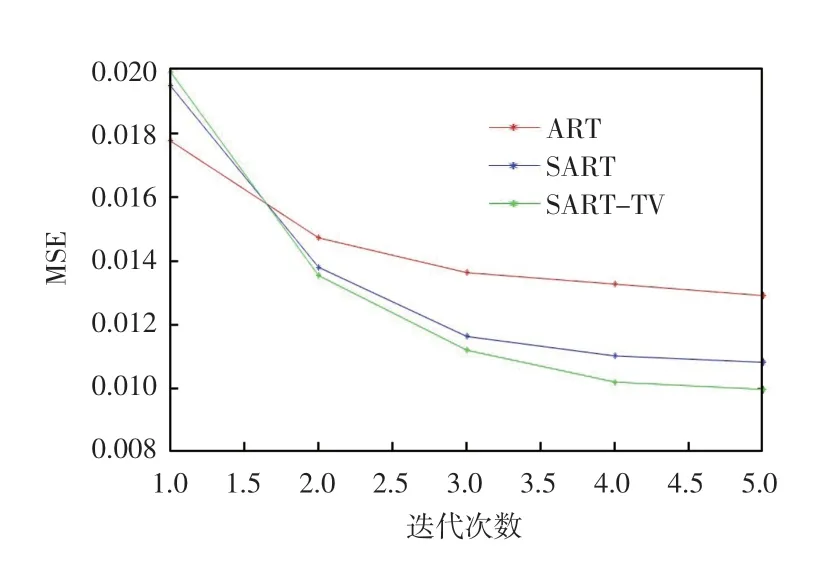
图6 [0°，130°]下MSE 结果

图7 [0°，150°]下MSE 结果

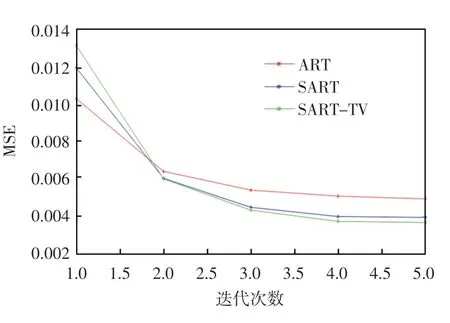
图8 [0°，170°]下MSE 结果

3 结语

本文利用4 种算法对Shepp-Logan 头模型进行了实验，对稀疏角度和有限角度投影数据进行图像重建，并分析每种算法的优缺点及适用情况。通过对重建图像效果分析可知，用Shepp-Logan 头模型进行实验时，迭代类重建算法的重建效果比解析类好，重建效果的优劣依次为：SART-TV、SART、ART、FBP。但是，每种算法都有其局限性，并不能在所有情况下都能重建出完美的图像，同时迭代类的算法还会受迭代次数以及松弛因子的影响且算法耗时长。此问题还需要进一步研究，今后针对不同的模型进行实验，提出更适用的改进算法。