具有半封闭非选择性捕获种群模型研究进展

雷朝铨 ,张馨馨 ,许丽莉

（1.宁德师范学院 数理学院，福建 宁德 352100;2.福州大学 数学与计算机科学学院，福建 福州 350016）

随着社会的不断发展，人类对自然资源的开发更加迫切.但是为了维持生态系统的持续稳定，人类不能无限制地开发自然资源，而应对其合理开发，如为了保护野生动物建立自然保护区，从而限制对野生动物的捕获，使得各物种能够稳定地维持在可持续状态.因此研究具有非选择性和半封闭捕获的模型对维持生态系统的稳定性具有重要意义.2013 年，Kunal 等[1]首次提出具有半封闭非选择性捕获的捕食-食饵系统，近年来学者们在该方向展开了大量的研究，取得了丰富的成果，特别宁德师范学院的林启法、雷朝铨在该方向做了较好的工作，试图对国内外的研究进展进行归纳，使得有心从事该方向研究的学者能快速地了解国际上的相关进展.

1 具有非选择性和半封闭捕获捕食食饵模型的研究进展

Chakraborty 等[1]提出了如下具有非选择性和半封闭捕获的Beddington-DeAngeli 功能性反应捕食-食饵系统:

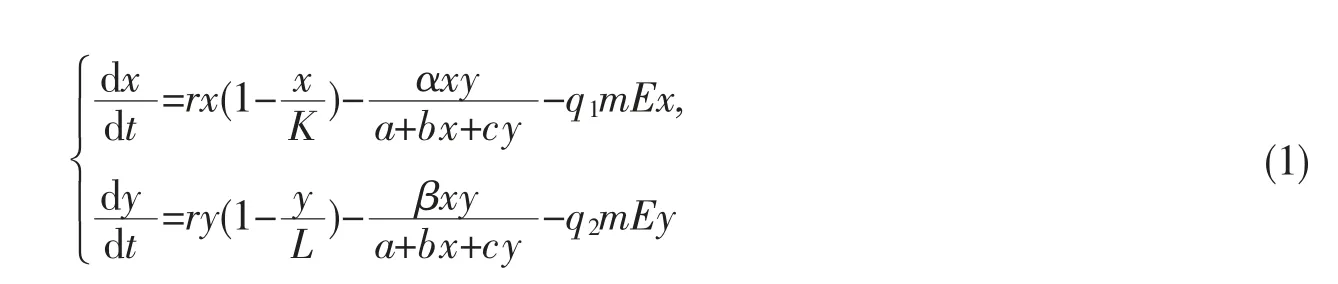
平衡点局部稳定的充分条件，其次通过构造适当的Lyapunov 函数得到正平衡点全局稳定的充分条件.但是由于系统过于复杂,作者未能对参数m 如何影响系统的动力学行为给出明确的理论分析，同时也没有对边界平衡点的稳定性进行研究.

由于式（1）过于复杂而无法明确地对m 如何影响系统的动力学行为进行探讨，因此刘羽等[2]在最简单的Lotka-Volterra 竞争系统基础上提出具有半封闭捕获两种群的Lotka-Volterra 捕食-食饵系统:

作者的研究表明无论捕捞努力量多大，只要捕捞区域被限制得足够小，则两个物种均能持续生存；若捕捞区域过大，即使人类不能进入封闭区域进行捕捞，物种最终都将灭绝.

Zhang等[3]提出了波动水位下具有非选择性捕获的捕食-食饵模型：

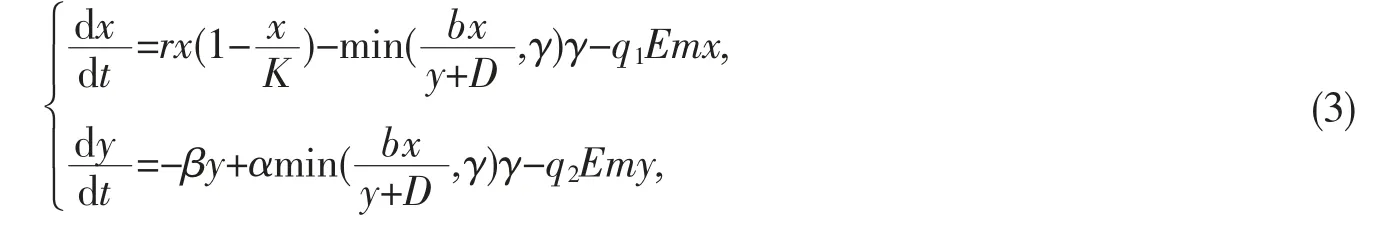
2 具有非选择性和半封闭捕获偏利、偏害或者合作种群模型的研究进展

偏利、偏害或者合作是自然界中较为常见的3 种种间关系，学者们对非选择性半封闭捕获如何影响这3 类系统的动力学行为展开了系列研究.

Lin 等[4]受式(1)启发，建立了半封闭条件下具有非选择性捕获和非单调功能反应的两个种群偏利共生模型：

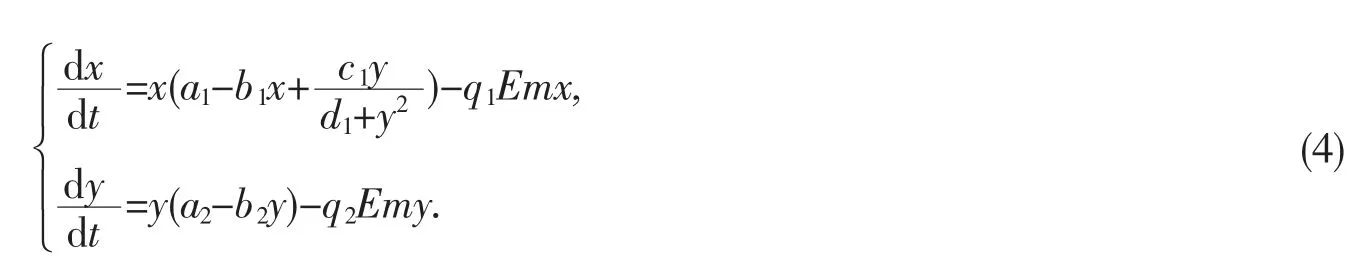
其研究表明：受参数m 的影响，系统中两个生物可能同时灭绝，或者一个灭绝而另一个稳定存在，或两个种群能持续共存.没有捕获的系统存在唯一的全局吸引的正平衡点，相比之下，捕获极大地改变了系统的动力学行为.

Huang 等[5]提出具有非选择性捕获和半封闭捕获的Lotka-Volterra 偏利共生模型：

作者讨论了式（5）平衡点局部稳定性和全局稳定的条件；同时得出若平衡点是局部稳定，定为全局稳定，若正平衡点存在，则必为全局渐近稳定.此外对正平衡点E(x*,y*)，x*,y*是关于m 的严格递减函数，进而分析得出为了保证两个种群共存，捕捞比例m 不能太大，否则至少有一个种群将趋于灭绝.

Liu 等[6]提出如下具有非选择性和半封闭捕获的非自治偏利共生模型：

作者分析了式（6）的持久性和绝灭性，得出根据可捕捞区域的变化，系统可能表现出持久性、绝灭性或残存性.

合作是两个种群之间最基本的关系，Lei[7]提出具有半封闭和非选择捕获的合作系统：

作者研究了式（7）平衡点E0(0,0)，,E4(x*,y*)的存在条件和局部稳定性，同时利用微分不等式理论得到边界平衡点全局吸引的充分条件：

有趣的是，对比平衡点局部稳定性和全局吸引的充分条件可以看出平衡点的局部稳定性就能保证全局吸引.同时作者还发现尽管ki、ai(i=1,2)影响种群的最终密度，但对系统的持久性没有影响；通过数值模拟发现当种群的内禀增长率足够大且捕获区域被限制在合适范围内，两个种群能够长期共存.

偏害也是种群之间的一种共存关系，指的是两个种群之间的一种共存作用,这种作用使得其中一个种群从另一个种群受到损害而对另一个种群没有影响.

Chen[13]建立了半封闭条件下具有非选择性捕获的偏害共生Lotka-Volterra 模型：

作者首先研究了系统平衡点的存在性、局部稳定性和全局稳定性，得出如下结论：1)系统正平衡点存在必是全局渐近稳定的；2)平衡点若是局部稳定必定是全局渐近稳定的.

然后根据正平衡点D(x*,y*)全局渐近稳定的充分条件和参数m 的生物意义得出：当种群的可捕捞比例较小时，无论两种群初始状态如何，两个种群都可持续共存.

最后通过对正平衡点D(x*,y*)的x*、y*关于m 求导发现x*、y*均为关于m 的递减函数，即捕获面积越大，种群最终的数量越少.

近年来，越来越多学者发现，对于寿命短、世代不重叠的种群或者种群数目较小，在某时间间隔内形成一代，那么离散数学模型比连续模型更符合实际.基于Chen[8]的工作，Su 和Chen[9]提出具有半封闭条件下具有非选择性捕获离散的Lotka-Volterra 偏害模型：

作者利用差分不等式得到系统持久性和绝灭性的充分条件：

3 具有非选择性和半封闭捕获阶段结构种群模型的研究进展

很多动物一生都要经历几个明显的阶段,因此阶段结构种群模型一直是学者们研究的热点之一.Xiao 等[10]首次提出具有非选择性和半封闭捕获单种群模型：

通过分析，作者得出该系统平衡点存在情况和稳定性，进而得出如下结论：在种群出生率和死亡率较为合理的情况下，可捕捞比例m 是种群灭绝的决定性因素；当m 越小，则种群最终稳定下来的数量越大，反之则越小，当m 大于某个值时，种群将灭绝.这启示人类需要建立一定大小的保护区对种群捕获进行限制，过小的保护区起不到保护种群的作用.

最近，Wang 等[11]也考虑出生率为非线性的情况，对半封闭条件下具有非选择性捕获和非线性出生率的单种群模型进行研究：

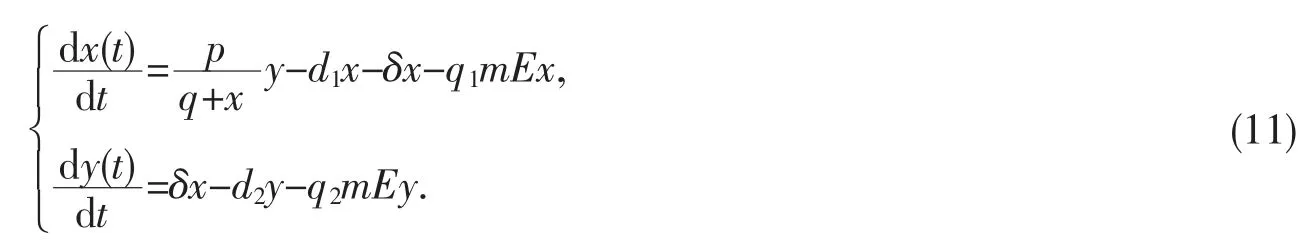
在该模型中作者假设幼年种群和成年种群都可被捕获.证得正平衡点存在必为全局渐近稳定.其后，对m 如何影响系统动力学行为展开了详尽的分析.

4 总结

自Kunal 等[1]首次提出具有半封闭捕获的捕食-食饵系统以来，学者们探讨了半封闭捕获对其他类型的种群，如偏利、偏害、合作、阶段结构单种群模型等的影响，得到了一些很好的结果.

由于这一方向研究起步较晚，尚有大量的问题有待研究：如考虑非选择性半封闭捕获对具有恐惧效应的Lotka-Volterra 捕食-食饵模型的动力性行为影响；非选择性半封闭捕获对具有反馈控制的两种群Lotka-Volterra 合作系统模型的影响；非线性选择性捕获对竞争系统种群模型的动力学行为影响等等.