公路线形安全性新型隶属函数关系模糊评价
2021-10-16刘永顺
刘永顺
(中国人民公安大学,北京 100038)
引言
在我国公路纵横交错、四通八达的同时,也带来了更多的交通安全问题。线形作为公路的骨架,在公路总体布局与设计中起着决定性作用,仅在2019 年,由于道路线形引起的事故起数达到247 646起,造成20.44 万人受伤、4.74 万人死亡[1]。因此,有效地线形评价是保证线路设计合理以及行车安全的重要一环,很多专家学者对线形安全设计进行了研究。LIU 等[2]选择坡度方向、高差绝对值、高程标准差、曲线半径、过渡曲线比来描述道路线形特征,建立二元Logistic 回归模型,分析线形因素对事故的影响。LI 和KAN[3]建立了回归模型,分析了过渡曲线长度、圆形曲线半径等对交通安全的影响。郭忠印等[4]利用流量与车速的关系建立基于标准通行能力的理论分析模型,以相邻路段标准通行能力差作为道路线形安全评价指标进行研究。符锌砂和龙昱[5]通过速度、线形、舒适性、总体线形连续性、弯道密度进行模糊综合评价。
公路线形评价的难点在于如何更准确地定量分析评价指标,评价方法既要做到避免主观性,又要保证客观性不脱离实际。线形安全的影响因素很多,且具有模糊性,因此,可以采用模糊综合评价法。以往模糊评价研究大多基于运行速度指标与线形之间的关系[6]或者依赖于操作繁琐的专家打分法[7-8],前者将其运用到工程中时仍存在实用性欠缺的问题,后者受人为主观影响较大,因此,依据规范[9-10]要求提出改进的评分标准,通过新型隶属度函数建立模糊关系矩阵,为公路线形设计提供综合评价方法。
1 公路线形安全性评价指标体系
采用层次分析法(AHP)进行分析,通过对平面、纵断面及横断面相关指标进行筛选,确立了具有三层次结构的评价体系,即目标层、准则层和指标层,见图1。
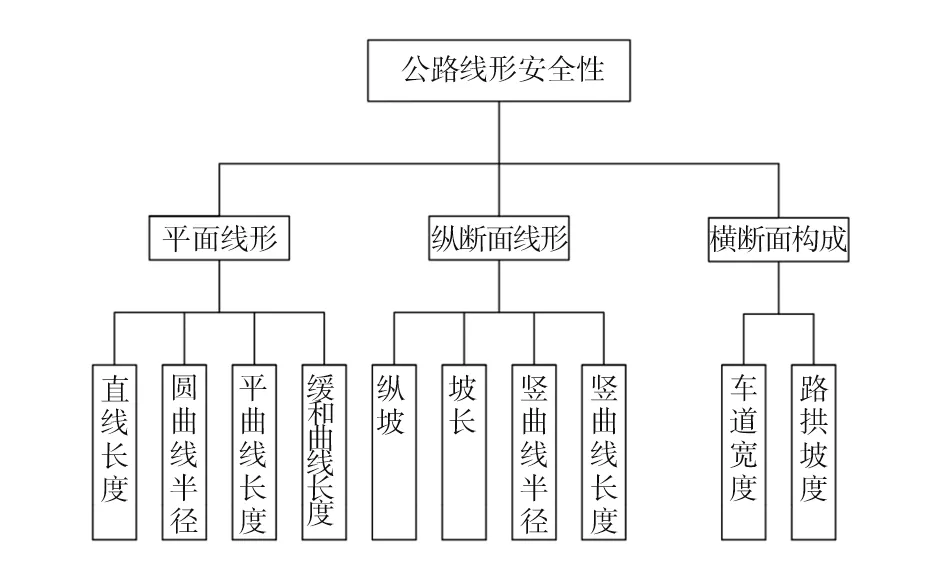
图1 公路线形安全性评价指标体系
1.1 直线长度
在由线形引发的事故中,平直路段占比超过80 %,对于计算设计速度≥ 60 km/h 的公路,同向曲线间直线长度不小于6 倍设计时速,最大直线长度一般不超过 20 倍设计时速。以设计时速为80 km/h的一级公路作为研究对象,故直线长度应介于480 m和1 600 m 之间。
1.2 圆曲线半径
为保证行车舒适,圆曲线半径设置不宜过小,圆曲线最小半径的确定与设计速度相关,同时又要减少半径过大对测设和施工的不利影响,最大半径不宜超过10 000 m,当设计时速为80 km/h 时,圆曲线半径不宜<400 m。因此,圆曲线半径应介于400 m 和10 000 m 之间。
1.3 平曲线长度
当平曲线长度较小时,由于离心力的作用,会让驾驶员产生操作突变感,因此,应对平曲线长度下限加以限制,当设计时速为80 km/h 时,平曲线长度应>400 m。
1.4 缓和曲线长度
为便于驾驶员的操作,减少离心力变化带来的乘车舒适性及行车平稳性,应在圆曲线与直线之间加一段一定长度的过渡线性,当设计时速为80 km/h时,缓和曲线长度应>70 m。
1.5 纵坡
为使车辆行驶平顺,公路纵向起伏不宜过大且过于频繁,同时又要考虑路面排水所需,公路纵坡不宜小于0.3 %,当设计时速为80 km/h 时,最大纵坡为5 %,因此,纵坡应介于0.3 %和5 %之间。
1.6 坡长
坡长过长或过短都会造成驾驶员情绪紧张,易造成操作失误,引发交通事故,因此,要对其坡长加以限制,当设计时速为80 m/h 时,其值应介于200 m 和700 m 之间。
1.7 竖曲线半径及长度
竖曲线半径大小及其长度直接影响着行车视距及驾驶安全性,当设计时速为80 km/h 时,凸型竖曲线半径应>4 500 m 为宜,凹形竖曲线半径应>3 000 m为宜,且其长度都应>70 m。
1.8 车道宽度
车道宽度影响着驾驶舒适性,过窄会造成驾驶员情绪紧张,过宽会浪费土地资源,当设计时速为80 km/h 时,一级公路车道宽度应取3.75 m 为宜,且随着道路等级的降低可适当减少。
1.9 路拱坡度
一级公路整体式路基的路拱一般采用双向路拱坡度,为便于路面排水以及车辆平顺行驶,路拱坡度宜为2%且不应小于1.5%。
2 模糊综合评价方法
2.1 确定评价因素集
根据图1 确定评价因素,模型采用二级模糊评判法[11]。
评价集U={U1,U2,U3}={平面线形,纵断面线形,横断面构成}。
2.2 建立子评价因素集
U1={U11,U12,U13,U14}={直线长度,圆曲线半径,平曲线长度,缓和曲线长度};
U2={U21,U22,U23}={坡度,坡长,竖曲线半径,竖曲线长度};
U3={U31,U32}={车道宽度,路拱坡度}。
2.3 确定各因素权重向量
评价指标权重反映其对评价目标的重要程度。采用层次分析法确定指标权重,对两两因素间进行重要程度的比较,利用yaahp 软件构造判断矩阵并进行一致性检验,求得各层级指标权重向量见表1 ~表4。
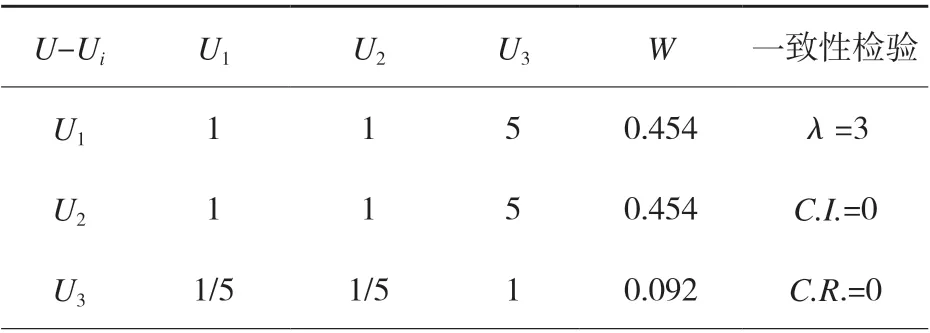
表1 准则层权重向量计算结果
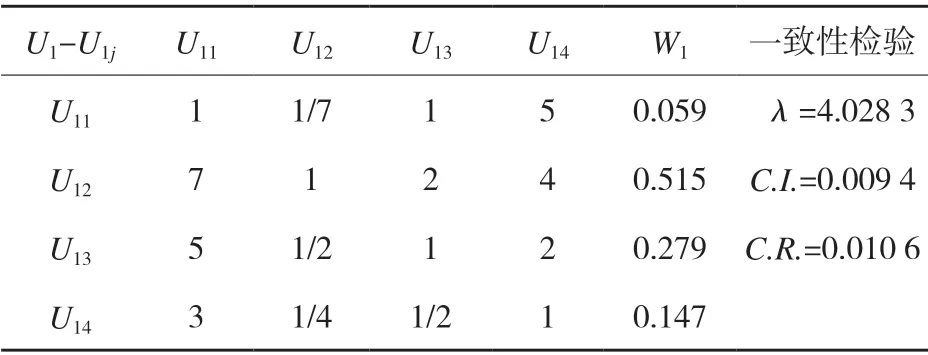
表2 第一准则层权重向量计算结果

表3 第二准则层权重向量计算结果
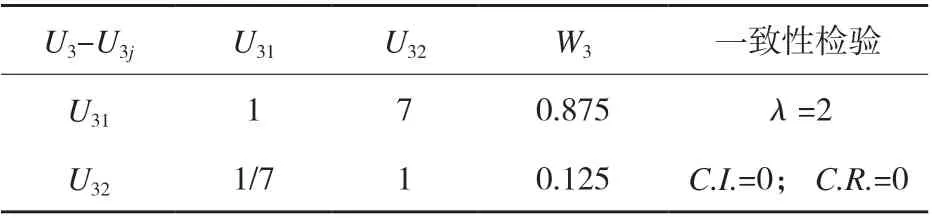
表4 第三准则层权重向量计算结果
2.4 建立评语集
评语集是评判者对公路线形安全性评价可能得出的评判结果所组成的集合。
评语集V={V1,V2,V3}={ 优,良,差},其中评分在85 ~100 之间的属于“优”级别,评分在70 ~85 之间属于“良”级别,在55 ~70 之间属于“差”级别。
2.5 建立基于新型隶属函数的模糊关系矩阵
模糊关系矩阵R([rij])是从评价集U 出发进行评价,以确定评价对象对评语集元素V 的隶属度,其中rij表示评价因素Ui对于第j 个评语集的隶属度。由此,可得到单因素模糊评价集Rij,并由其组成评价矩阵R。该问题的隶属度函数由评判标准确定,评判标准根据《公路路线设计规范》(JTG D20—2017)和《公路工程技术标准》(JTG B01—2014)等[9-10]规范及相关文献[12-13]中关于公路线形要素的标准确定,见表5。

表5 公路线形安全评价指标评判
隶属度由隶属度函数确定,见公式(1)~公式(3)。

2.6 确定模糊关系
将各因素权重向量W 与模糊关系矩阵R 相乘,便可得到模糊综合评价集。

式中:bi—评价指标对第i 个评语Vi的隶属度。根据最大隶属度原则,当存在i ∈[1,2,3]使bi最大时,则认为该评价集属于第i 个评语Vi,其中,1,2,3分别表示“优”“良”“差”级别。
2.7 进行模糊综合评价
通过上述方法,可以由指标层评价准则层,再由准则层的评价结果来得到公路线形安全性的综合评价结果。

式中:Bi—指标层对准则层的隶属度;B—准则层对目标层的综合评价矩阵,即公路线形安全性的隶属度。由此可得到公路线形的安全性。
3 线形安全指数
线形安全指数是通过评价结果加权平均的方法,得到线形评价最终得分。
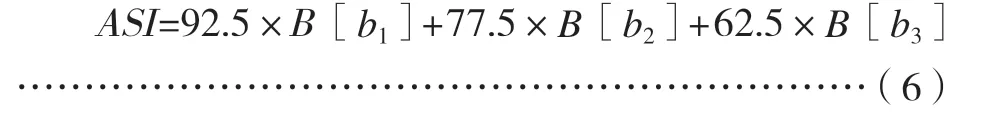
式中:B[bi]—公路线形安全性评级为“优”“良”“差”的隶属度,而“92.5”“77.5”“62.5”分别为三个评级的阈值。
4 工程应用
甘肃省兰州-永登高速公路C 标段全长5.326 km,设计时速为80 km/h。参照评分准则,采用内插法,将该路段线形设计平面图每相邻拐点间线段进行各自区间平面线形打分并取其平均值,以纵断面图每相邻拐点间线段进行各自纵断面线形打分并取其平均值,各指标得分值见表6。

表6 指标得分值
4.1 隶属度计算
根据公式(1)~公式(3)的隶属度函数得出各参数指标的隶属度Rij,并将其归一化,得单因素评价集:

4.2 模糊综合评价
根据表2 ~表4 的指标层权重系数,按公式(5)进行运算,可得准则层Ui的隶属度。

(4)公路线形安全性U 隶属度
根据准则层权重系数及公式(5),得出综合评价。

(5)评价结果
通过建立的基于《公路路线设计规范》(JTG D20—2017)等标准的新型隶属函数关系,根据最大隶属度原则,该公路属于“优”“良”“差”的隶属度分别为0.367、0.452、0.181,因此,该路段的安全性评价为“良”。
4.3 线形安全指数
由公式(6)计算得到线形安全指数为80.3,说明该路段的安全性综合评价等级同最大隶属度原则结果相同,也为“良”。一般可以认为该路段的公路线形是安全的,但依然存在一些指标如“直线段长度”设置不当的情况,还需通过改善路段的交通设施、调整路段弯道个数等措施提醒驾驶者谨慎驾驶,提高该路段的线形安全性。
5 结语
将层次分析法与隶属函数模糊评价法相结合来评价公路线形的良好程度,运用模糊数学概念,对隶属函数关系建立方法提出改进,可以在复杂系统中较准确地评价公路线形的安全性。但本研究涉及的线形设计参数还不够精细,没有考虑到线路转角、超高及道路加宽的影响,具体计算有待进一步的研究。
