矮塔斜拉桥设计参数对主梁受力及变形的影响

王汪阳

（新疆兵团勘测设计院（集团）有限责任公司，新疆 乌鲁木齐 830002）

引言

近年来，矮塔斜拉桥因具有外型美观、经济合理、施工简便及跨径布置灵活等特点，逐渐在我国桥梁事业中得到广泛应用［1］。但在早期完工的矮塔斜拉桥工程中，由于设计者对桥梁部分参数的分析不足，导致桥梁出现主梁大幅度变形、受力不均等严重病害［2-3］。因此，为保障矮塔斜拉桥运营的安全性，深入研究其参数设计具有重要意义［4］。

目前，国内外学者关于斜拉桥的参数设计问题展开了大量研究，张欣欣［5］针对矮塔斜拉桥结构体系、合理结构参数、斜拉索张拉方案等关键技术进行分析研究，发现采用刚构连续梁体系，辅以外伸跨，可以有效地减小下部结构受力，同时满足刚度要求，结构经济合理。鲍英基等［6］对PC 矮塔斜拉桥运营阶段主梁的应力和位移进行敏感性分析，得出主梁应力和位移随各参数的变化规律。上述学者主要是针对传统斜拉桥进行的参数设计研究，而关于矮塔斜拉桥的参数设计研究还有待进一步完善。

1 工程概况

某大跨度双塔混凝土矮塔斜拉桥+先简支后连续预应力T 梁组合体系桥梁全长475 m，主桥跨径布置为80 m+145 m+80 m，引桥跨径布置分别为2×40 m和3×30 m，桥面总宽25 m，包含2×0.5 m 防撞护栏+2×11 m 行车道+2 m 中央隔离带。道路设计为双向四车道，设计速度为80 km/h，设计荷载为公路-Ⅰ级，地震动峰值加速度为0.2 g。矮塔斜拉桥主梁采用单箱三室斜腹板变截面箱梁，顶板宽12 m，底板宽6.8 m，支点处梁高5.8 m，跨中梁高2.8 m，呈二次抛物线形式变化，斜拉索张拉位置的箱梁内每隔6 m 设置一横隔板，厚度为40 cm。主梁与主塔采用塔梁固结体系，主塔采用矩形断面，截面尺寸为5 m×2.4 m，桥面以上塔高为24 m，主塔对称设置斜拉索17 对，呈单索面扇形布置。梁上间距为7 m，塔上间距为1 m，边跨无索区长度为18 m，中跨无索区长度为21 m，斜拉索通过塔身分丝管鞍座，对称锚固于梁体上，间隔1 m。矮塔斜拉桥总体布置见图1。

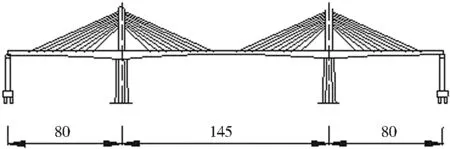
图1 矮塔斜拉桥总体布置/m

2 建立模型

运用软件Midas/Civil 建立矮塔斜拉桥有限元模型，其中主梁、主塔及桥墩均采用梁单元模拟，采用桁架单元模拟斜拉索，全桥共包含58 个桁架单元、182 个梁单元和276 个节点，有限元模型见图2。

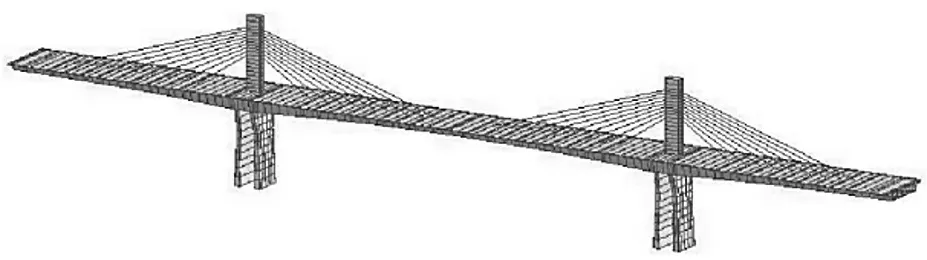
图2 矮塔斜拉桥有限元模型

计算过程中考虑初始张拉力的影响，斜拉索的初始张拉力均为5 600 kN，斜拉索的弹性模量取值按钢绞线实际弹性模量，但考虑到防腐材料的重量，斜拉索的容重增加10%。主梁与主塔节点之间采用固结连接形式，主梁与桥墩节点采用刚接连接形式，不考虑主梁、主塔及桥墩的几何非线性变形对结构的影响，模型基础边界条件采用相应刚度矩阵方法模拟。计算荷载主要考虑恒载、活载、挂篮与湿重荷载，混凝土的收缩徐变作用及温度荷载的影响。钢绞线及预应力钢筋计算参数见表1。

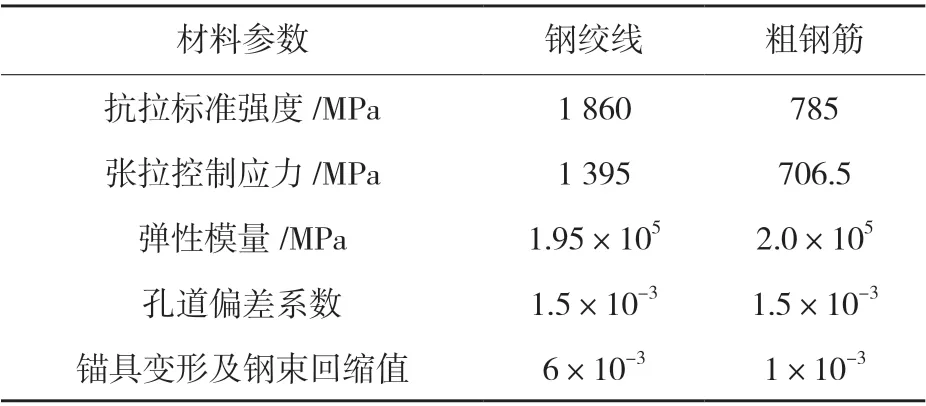
表1 钢绞线及预应力钢筋计算参数

3 结果分析

在矮塔斜拉桥的设计中，边中跨比与主塔高度的参数选取是一个非常重要的结构参数设计步骤，合理的参数选取可有效提升矮塔斜拉桥的经济性和力学性能。为了研究参数对矮塔斜拉桥的影响，通过建立模型对桥梁受力及变形情况展开对比分析。

3.1 边中跨比

建立边中跨比分别为0.52、0.54、0.56、0.58 及0.6 的矮塔斜拉桥模型。针对不同边中跨比的主梁边、中跨挠度及弯矩进行计算，得到最大挠度及弯矩变化曲线见图3。

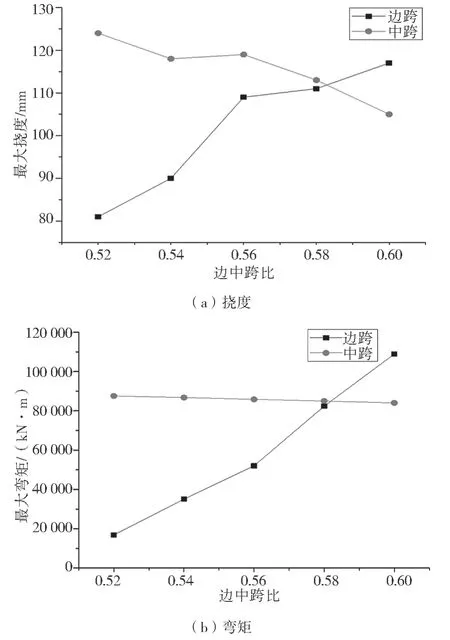
图3 最大挠度及弯矩变化曲线

根据图3 可知：（1）随着矮塔斜拉桥边中跨比不断增大，主梁边跨的最大挠度呈增大的趋势，而中跨最大挠度呈减小的趋势变化，说明边中跨比对矮塔斜拉桥变形的影响较大。当边中跨比由0.52 增至0.6 时，主梁边跨最大挠度由81 mm 增至117 mm，增幅为41.3%，而中跨最大挠度由124 mm 减小至105 mm，减幅为15.3%，说明增大边中跨比虽然可以一定程度降低主梁中跨变形量，但会大幅度增大边跨变形量。（2）随着矮塔斜拉桥边中跨比的增大，主梁边跨最大弯矩均呈不断增大的趋势，中跨的最大弯矩呈缓慢减小的趋势，说明边中跨比对矮塔斜拉桥受力存在影响。当边中跨比由0.52 增至0.6时，主梁边跨最大弯矩由16 846 kN·m 增至108 886 kN·m，增幅为546%。而主梁中跨最大弯矩由87 525 kN·m 减至84 002 kN·m，减幅为4%，说明增大边中跨比会大幅度增加矮塔斜拉桥主梁边跨受力，不利于结构的安全性。

3.2 主塔高度

建立塔高分别为18 m、22 m、26 m、30 m 及34 m的矮塔斜拉桥模型，针对不同塔高的桥梁边、中跨挠度及弯矩进行计算，得到最大挠度及弯矩变化曲线见图4。

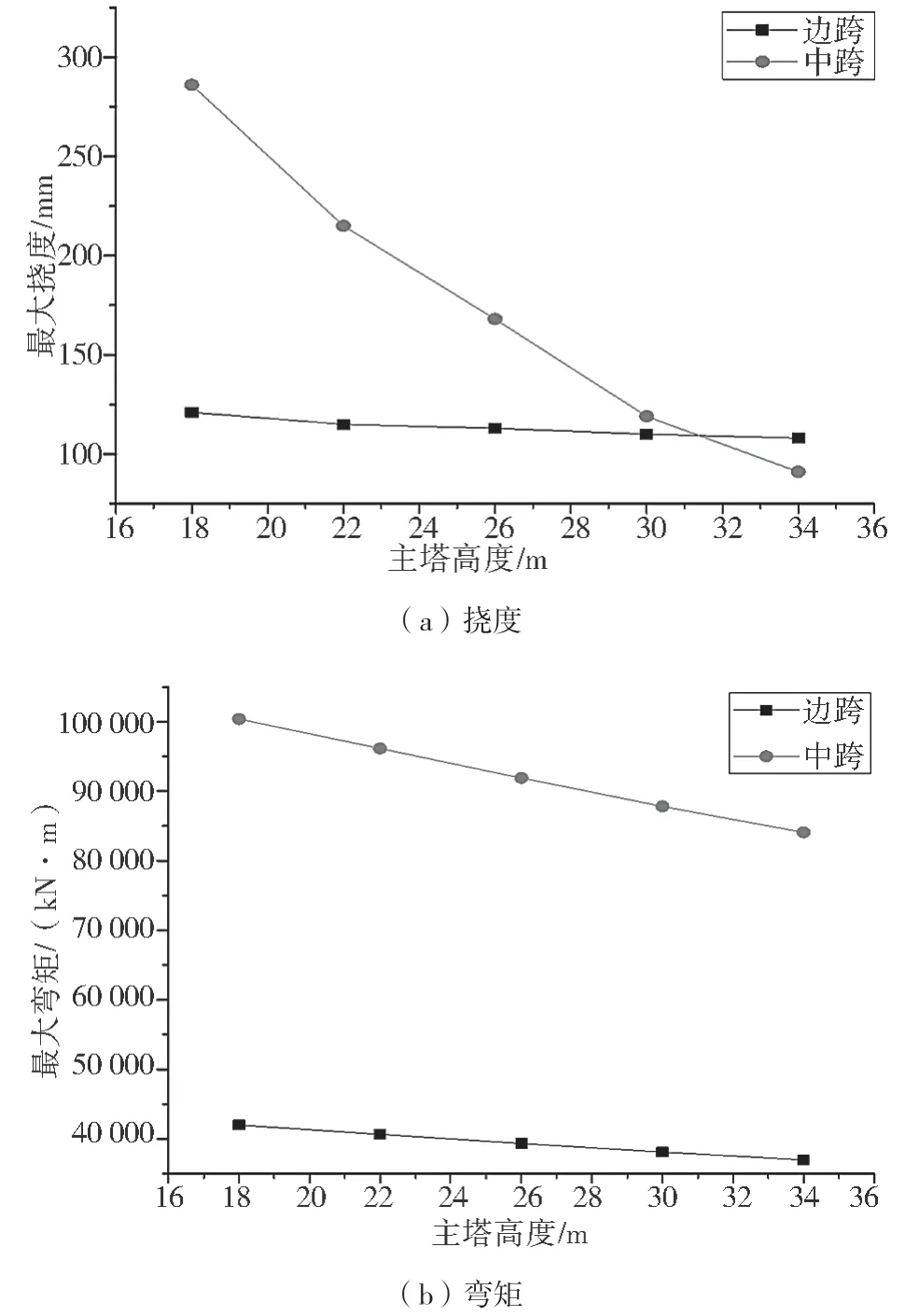
图4 最大挠度及弯矩变化曲线

根据图4 可知：（1）矮塔斜拉桥边、中跨最大挠度均随着主塔高度的增大而不断减小，说明边中跨比对矮塔斜拉桥变形的影响较大。当主塔高度由18 m 增至34 m 时，主梁边跨最大挠度由121 mm减至108 mm，减幅为10.7%，而中跨最大挠度由286 mm 减小至91 mm，减幅为68.1%，说明增大主塔高度可以大幅度降低主梁中跨的变形量。（2）随着矮塔斜拉桥主塔高度的增大，主梁边、中跨最大弯矩均呈不断减小趋势，说明边中跨比对矮塔斜拉桥受力存在影响。当主塔高度由18 m 增至34 m 时，主梁边跨最大弯矩由42 003 kN·m 减至36 984 kN·m，减幅为11.9%，而主梁中跨最大弯矩由100 386 kN·m 减至84 071 kN·m，减幅为16.3%，说明增大主塔高度可以有效降低矮塔斜拉桥整体结构受力。

4 结语

（1）斜拉桥主梁中跨最大挠度随着边中跨比的增大逐渐减小，而主梁边跨的最大挠度随之逐渐增大；主梁中跨的最大弯矩随着边中跨比的增大呈略微减小，主梁边跨最大弯矩则随之逐渐增大；边中跨比过大对主梁边跨的挠度、弯矩影响明显。（2）随着主塔高度的增大，主梁边、中跨的最大挠度均逐渐减小，且边跨减幅更明显；主梁边、中跨的最大弯矩均随主塔高度的增大逐渐减小。