基于巷道分区和鸡群优化的井下WSNs定位算法

吴雪敏,张继荣

(西安邮电大学 通信与信息工程学院,陕西 西安 710061)

0 引 言

与地面上环境不同，巷道是狭长的且有较多分支，同时，井下环境高粉尘、高压强，湿度大。井下的复杂环境对定位算法存在较大制约。传统有线监控系统的布设成本高、线路易受损且抗干扰能力差，无法满足井下监控的需求。无线传感器网络(wireless sensor networks,WSNs)具有低成本、布设灵活及很强的扩展性等特点，可以很好地弥补传统监控系统的缺点，实现井下环境的全覆盖和实时监测。目前，针对井下WSNs监测系统的定位问题已有了一些经典算法。如王慧[1]提出一种基于巷道模型和节点分布模型的定位算法，首先利用高斯消去法筛选用于定位的锚节点，然后采用最小二乘法估计待测节点的位置，实现井下精确定位。邢智鹏等人[2]利用LQI(link quality indicator)对接收信号强度指示(received signal strength indication,RSSI)数据滤波，并估计信道参数和环境参数，利用环境参数修正RSSI的测距结果，最后采用最小二乘法计算未知节点坐标。朱光[3]提出一种改进RSSI加权质心定位算法，该算法由RSSI测距和加权质心定位两部分组成，提高了算法对井下环境的适应能力，但精度不够。余修武等人[4]考虑到随着时间的变化，传感器节点电池能量越低，导致RSSI值变小，从而影响定位精度的问题，提出一种巷道分区策略，将巷道分成长度相等的区域，利用节点接收到的RSSI值判断其所属区域，并将该区域的质心作为未知节点的估计位置，该算法虽实现简单，功耗低，但定位精度同样较差。

针对上述情况，本文提出一种基于巷道分区和鸡群优化(chicken swarm optimization,CSO)的WSNs井下定位算法，该算法首先对巷道分区，根据未知节点所属区域确定未知节点的粗略位置；然后，在未知节点所属区域内，利用改进的CSO算法通过迭代寻优以得到未知节点的精确位置。本文将定位问题转换为优化问题，利用群智能算法群体间良好的合作能力，确定未知节点的位置，以提高井下定位精度。

1 巷道分区

井下巷道长度一般可达数千米(km)，但宽度只有3～5 m，因此，相比于长度，巷道的宽度可以忽略。巷道中锚节点一般通过人工等距离布署，井下巷道分区模型如图1所示。首先，将两相邻锚节点间区域根据其水平距离进行等距分区，并将锚节点间的实际距离和信号强度作为已知条件，根据信号传播损耗模型计算出锚节点的发射信号到达各个分区的接收信号强度值RSSI；然后，将RSSI值根据大小分为不同等级，利用RSSI等级划分区域；最后，根据节点接收到的RSSI值所属等级确定节点所在区域。

图1 井下巷道分区模型

上图为巷道分区模型，其中，A，B，C，D，E，F为锚节点，将相邻锚节点按其水平距离等分。如图中，a，b，c，d，e为相邻锚节点的中点，假设任意两个相邻锚节点间的距离为L，则a点到锚节点A和B的水平距离均为L/2，a点到锚节点C的水平距离为3L/2，同理，可得其它各点间的距离。若未知节点收到来自锚节点的信号强度RSSI，则根据式(1)可得两者间的距离d，如式(2)所示

RSSI(d)=RSSI(d0)-10δlg(d/d0)+N(0,σ)

(1)

d=10[RSSI(d0)-RSSI(d/d0)+N(0,σ)]/10δ

(2)

式中RSSI(d)为距锚节点dm处接收信号的强度值，d0为距离锚节点1 m，N(0,σ)为正态分布函数，δ为路径衰减因子，它一般在2～6之间取值。

将式(1)简化可得

RSSI(d)=RSSI(d0)-10δlg(d)+N(0,σ)

(3)

假设锚节点C和未知节点g收到来自锚节点A的信号，则由式(3)可得，节点C和g的接收信号强度分别为

RSSI(dAC)=RSSI(d0)-10δlg(dAC)+N(0,σ1)

(4)

RSSI(dAg)=RSSI(d0)-10δlg(dAg)+N(0,σ2)

(5)

由式(4)和式(5)可得

RSSI(dAg)=RSSI(dAC)-10δlg(dAg/dAC)+N(0,σ)

(6)

由于N(0,σ)很小，可将其省略，简化后的公式为

RSSI(dAg)=RSSI(dAC)-10δlg(dAg/dAC)

(7)

由式(7)可得点a，B，b接收到节点A的信号强度为

(8)

式中 显然a点的RSSI值最大，B点次之，b点最小。因此，可根据信号接收强度划分区域，若未知节点g接收到来自锚节点A的信号强度RSSI(dAg)≥RSSI(dAa)，则记为一等强度A1；若RSSI(dAB)≤RSSI(dAg)≤RSSI(dAa)，则记为二等强度A2；若RSSI(dAb)≤RSSI(dAg)≤RSSI(dAB)，则记为三等强度A3，若小于RSSI(dAb)，不记。

根据上述方法，可对分区进行等级编码，如图1中未知节点g，根据其接收到的信号强度，可对其位置区域编码为A2B1C3。同理，可将巷道中其他分区编码为A3B1C2，B2C1D3，B3C1D2等，不同编码对应不同的接收信号强度以及不同的区域。未知节点可根据自身接收到周围锚节点的信号强度和对应的编码判断其所属区域。

2 CSO算法与改进

2.1 CSO算法

CSO算法是Meng X等人根据鸡群觅食行为提出的一种群智能优化算法[5]。该算法根据雄鸡个数将鸡群划分为若干子群，雌鸡和小鸡随机加入各子群中。其中，雄鸡有较好的适应度值，可以在更大空间内寻找食物；雌鸡的适应度值次之，雌鸡追随其所在子群中的雄鸡寻找食物；小鸡的适应度值最差，小鸡跟随鸡妈妈寻找食物，鸡妈妈由子群中的雌鸡个体中随机产生并与小鸡随机组成母子关系，每只鸡妈妈可以有多只小鸡。进化G代后，重新分配鸡群的等级制度。鸡群中不同等级个体的位置更新如下。

雄鸡位置更新公式

(9)

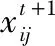
雌鸡位置更新公式

(10)

式中rand为[0,1]间的随机数，r1为第i只雌鸡所在子群中的雄鸡个体，r2为除r1之外的整个鸡群中雄鸡和雌鸡的任意个体。

小鸡位置更新公式

(11)

式中m为鸡妈妈，FL为跟随系数，取值范围为[0,2]。

2.2 基于行为反馈的雄鸡位置更新

CSO中，雄鸡相比于雌鸡和小鸡，具有最优的适应度值。在同一子群中，雌鸡的位置更新受雄鸡行为的影响，小鸡的位置更新受雌鸡行为的影响。由此可得，雄鸡的行为影响着整个鸡群的行为，一旦雄鸡陷入局部最优将使整个鸡群易陷入局部最优。因此，雄鸡是否可以避免陷入局部最优是整个优化过程的关键。

分析式(9)可知，假如雄鸡拥有更优的适应度值，则它的搜索范围更大。然而，根据CSO优化规则，当个体的适应度值更优时，表明其距离食物更近，此时应该在小范围内搜索才更可能找到食物。因此，拥有更优适应度值的雄鸡，其搜索范围应该更小。同时，雄鸡利用高斯随机搜索策略更新自身位置，没有考虑与其他个体的信息交换。在整个鸡群中，一方面，由于雌鸡的个数最多，在CSO的精度及寻优速度方面有重要的作用[6]；另一方面，雌鸡是连接雄鸡和小鸡的纽带，在鸡群中起承上启下的作用[7]。因此，本文在雄鸡的位置更新中加入雌鸡行为的反馈信息，使其不易陷入局部最优。改进的雄鸡位置更新公式如下

(12)

(13)

S=exp(fmean-fi)

(14)

式中S为反馈系数，fmean为跟随该雄鸡的所有雌鸡个体适应度值的均值，S越大表明雄鸡与雌鸡的适应度值相差越大，即雄鸡越偏离雌鸡群体。

式(12)～式(14)表明雄鸡的适应度值越小，即雄鸡具有更优的适应度值时，σ2越小，可以保证雄鸡在小范围内快速找到食物。同理，当雄鸡适应度值越大时，为了快速找到食物，其会在较大范围内搜索。同时，S≥1，当雄鸡越偏离雌鸡群体时，S越大，此时会增大雄鸡的搜索步长，当雄鸡越接近雌鸡群体时，S的值趋于1，此时雄鸡的局部搜索能力较强。

2.3 差分变异

CSO算法中鸡群个体的多样性会随着算法不断迭代而下降，导致算法容易过早收敛陷入局部最优解。为改进这一问题，引入了差分进化(differential evolution，DE)算法中的差分变异思想，当算法陷入停滞状态时，在鸡群中随机选取20 %的个体进行变异操作以达到增加种群多样性的目的。变异公式如下

(15)

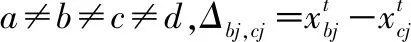
改进CSO算法的具体实现流程图如图2。

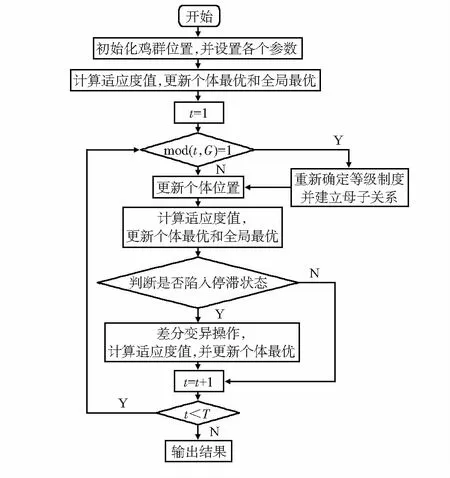
图2 改进CSO算法流程图

3 井下节点定位算法

3.1 适应度函数设计

在WSNs定位系统中，假设未知节点和信标节点坐标分别为(x,y)和(xi,yi)，i=1,2,3,…，n，则未知节点与各信标节点间的距离di可表示为

(16)

因此，WSNs节点定位算法的适应度函数可以定义为

(17)

通过上式将定位问题转化为求解最小值问题，CSO算法将每个可能解看作鸡群中个体的位置，计算每只个体的适应度值，通过不断迭代寻优，最终获得适应度值最优的个体，其位置即为未知节点坐标。

3.2 节点定位

经过巷道分区后可以确定未知节点所在区域，在该区域中，利用改进的CSO进行全局搜索，以实现对未知节点的精确定位。通过计算节点的定位误差error来评价本文算法的定位效果。公式如下

(18)

式中 (xi,yi)和(x′i,y′i)分别为未知节点i的实际坐标和计算坐标，N为未知节点总数。

井下节点定位的具体步骤为:1)在WSNs区域内部署节点，并设定通信半径R；2)按照本文第1节描述对巷道进行分区；3)根据未知节点接收信号强度确定其所属区域；4)利用本文改进的CSO算法迭代寻优，获得未知节点的坐标；5)利用式(18)计算本文定位算法的定位误差error；6)输出结果，算法结束。

3.3 仿真分析

通过MATLAB 2015b对本文算法与文献[3]中改进RSSI加权质心定位算法以及文献[4]中RSSP算法进行仿真对比。假设实验在图1所示巷道中进行，未知节点为50个，节点通信半径为40 m，鸡群总数为50，最大迭代次数为100次。各算法取重复50次的均值作为最终结果。定位系统的节点分布如图3所示。

图3 节点分布

1)三种算法定位误差对比

为对比本文算法、RSSI加权质心算法以及RSSP算法的定位误差，对三种算法进行仿真分析，结果如图4所示。

图4 三种算法定位误差对比

由图4可知，三种算法中，RSSP算法未知节点的最大定位误差为5.643 m，改进RSSI加权质心算法的最大定位误差为4.948 m，本文算法的最大定位误差为 2.903 m，明显小于另外两种算法，并且文献RSSP算法的定位误差最大。表明本文算法相比其他两种算法对未知节点的定位更准确，具有更高的定位精度，更适用于井下环境。

2)锚节点间距对定位精度的影响

令锚节点间距分别为20,25,30,35,40 m，其他参数设置不变，RSSP算法、改进RSSI加权质心算法以及本文算法的定位误差如图5所示。

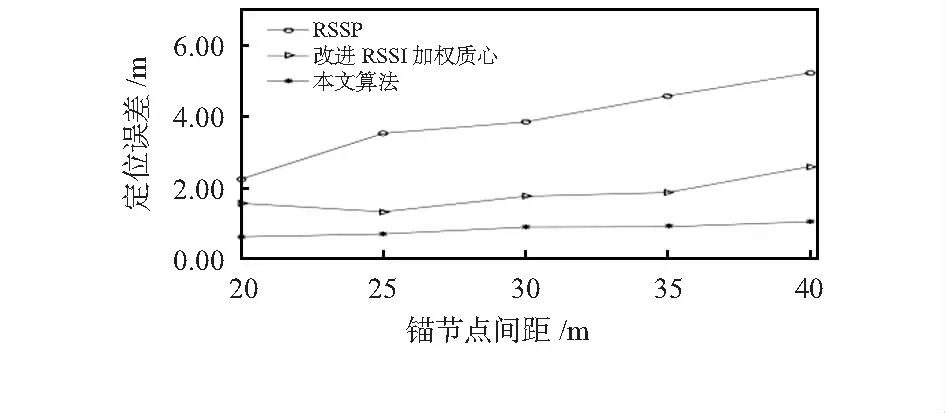
图5 锚节点间距对定位精度的影响

分析三条曲线可知，当锚节点间距从20 m增加到40 m时，三种算法的定位误差分别从 2.236,1.523,0.622 m增加到了 5.213,2.587,1.043 m。这表明，锚节点间距对三种算法的定位精度有不同大小的影响，RSSP算法在不同的锚节点间距处定位误差变化较大，且定位误差随着锚节点间距的增加而增大，相比而言，改进的RSSI加权质心算法和本文算法的定位误差受锚节点间距的影响较小，在锚节点间距不同的情况下，定位误差波动不大。同时，对比锚节点间距相同情况下三种算法的定位误差可得，本文算法的定位误差始终最小，因此，本文算法不但对锚节点密度要求较小，且具有更高的定位精度，即本文算法实现井下定位具有更好的效果。

3)测距误差对定位精度的影响

令RSSI测距公式中的正太分布函数标准差 的值分别等于1,1.5,2,2.5,3,3.5,4，其他参数不变，分别对三种算法进行仿真，结果如图6所示。

图6 测距误差对定位精度的影响

如图6所示，随着σ的增加，RSSP算法、改进RSSI加权质心算法以及本文算法的定位误差变化都较小，这表明三种算法都在较好的程度上克服了测距不准确对定位精度的影响。且总体来说，相比于RSSP算法和改进RSSI加权质心算法，本文算法具有更好的定位精度。

4 结 论

本文将定位问题转化为寻优问题，通过节点的RSSI值判断其所属区域，然后利用改进的CSO算法实现节点定位，最后通过实验证明了本文算法的有效性和优越性。