Ni–Al–Ru三元系1273K和1473K等温截面的试验和优化计算研究*

毛芯茹， 吴雪婷， 鲁晓刚，

（1.上海大学材料基因组工程研究院，上海 200444； 2.上海大学，上海 200444）

镍基高温合金具有优异的抗疲劳性能、韧性、高温蠕变强度、表面稳定性、抗氧化和抗热腐蚀性能，被广泛应用于航空航天领域，是目前用于制造先进航空发动机和工业燃气涡轮叶片等热端承载部件的主要用材[1]。然而随着服役环境越来越苛刻，镍基高温合金的开发面临着巨大的挑战，新的研发思路和方法应运而生。

随着计算材料科学的飞速进步，以计算热力学方法（CALPHAD）为基础构建的多尺度集成计算和试验平台， 是建立多元多相材料成分–工艺–组织结构–性能之间的定量关系、高效低耗设计先进工程材料的崭新手段， 也是材料基因组计划的终极目标[2]。这种新方法避免了传统试错法的许多缺点，节省了人力、物力，同时极大地提高了新材料设计的效率。CALPHAD 方法作为相图和热力学评估和计算手段，被广泛应用于新材料的设计和研发中[2–3]。

镍基高温合金中Ni–Al 系高温合金的主要强化相为L12–Ni3Al 结构的有序沉淀相（即γ′相）。经过研究发现[4–6]，元素Ru 对于提高Ni–Al合金的高温持久性能有重要的作用，但Ru 元素的过量添加会导致硬脆的TCP 有害相的析出，降低合金的蠕变性能[4]。因此，建立Ni–Al–Ru三元体系的热力学数据库对于掌握高温合金中析出相的相平衡关系及析出条件至关重要。

文献综述

在Ni–Al–Ru 三元体系中，Ni–Al 二元系的研究已经有大量报道。本研究中Ni–Al 二元系直接引用王杨[7]采用的热力学模型和优化的模型参数，计算得到的相图与前人的试验数据吻合得很好。

Al–Ru 二元系包含了大量的中间相。2003年Prins 等[8]根据前人的试验数据对该体系做了详细的评估，并给出了优化后的相图和热力学模型参数，其计算结果与试验数据吻合较好，可以用于外推至多元体系。

对于Ni–Ru 二元系，1961年Raub等[9]和1964年Kornilov 等[10]用差热分析法测得了液相线和固相线。两组测试的hcp 相的结果比较一致，但测得的fcc 相数据并不符合。而且所测的包晶反应（liquid+hcp→fcc）发生的温度相差很大，分别为1490℃和 （1550 ± 10）℃。另外，Kornilov 和Myasnikova[10]报道的包晶反应发生时Ru 在fcc 和hcp 相中的固溶度原子百分数分别为41.0%和53.0%，不同于Raub 等[9]报道的29.7%和51.3%。2002年Tryon 等[11]用纯Ni 和纯Ru 制备了1000 ℃、1100 ℃和1250 ℃时的扩散偶，使用电子探针显微分析（Electron probe micro–analysis，EPMA）技术测得3 个温度下的固溶度数据（原子百分数误差范围大约为1.0%），得到了fcc/hcp 两相区的结线 （Tie–line）。2004年Hallström[12]评估了以上3 组试验工作，并基于他们的相图试验数据利用CALPHAD方法给出了Ni–Ru 二元系的计算结果和优化后的热力学参数。2008年Hallström 等[13]研究Ni–Al–Ru 三 元系的相图时发现在2004年优化的二元体系的参数难以外推到三元系，所以结合第一性原理计算了亚稳的有序相的形成焓，重新对Ni–Ru 二元系进行了优化，计算相图与试验数据较为一致。2009年Okamoto[14]综合评估了前人研究的Ni–Ru 二元相图，相图上包晶反应发生的温度为1538℃，fcc 相在此温度时Ru 的固溶度原子百分数为31.1%，hcp 相的为51.0%，此结果与2008年Hallström[13]等的计算相图结果一致。

1986 年Chakravorty 等[15]详 细研究了1273K 和1523K 时Al 原子百分数为0 ～50%范围内Ni–Al–Ru 的等温截面，且根据1985年Chakravorty等[16]的研究，认为两个温度下都存在B2 相的溶解度间隙（即形成了基于B2–NiAl 的β1和基于B2–RuAl 的β2），当1273K时存在γ′+β1+β2和γ′+γ+β2三相平衡，1523K时存在γ+β1+β2和γ′+γ+β1三相平衡，并认为在1273～1523K 范围内，发生了反应：γ+β1→γ′+β2。此 后Horner等[17–18]在1997年报道了Al 原 子百分数低于50%和高于50%时Ni–Al–Ru 三元系的相图，但各相区的边界是模糊不准确的，此外还报道了一个新发现的三元相，其成分范围大约在Ni2Al14Ru，但尚未证实其正确性。2003年Mi 等[19]对富Al 区域不明确的相使用SEM、XRD、TEM 等测试手段测定了其晶格常数，确定了相的晶体结构，但并未给出具体的三元系相图。2006年Tryon 等[11]使用扩散偶法测定了Ni–NiAl–AlRu–Ru区域在1273K 和1373K 时的等温截面，并测得了元素的扩散通道。根据其试验结果认为B2 相区是连续的，即认为不存在B2 相的溶解度间隙。2008年Hallström 等[13]结合第一性原理计算和CALPHAD 方法，计算了1273K、1373K 和1523K 时的等温截面，但计算相图和试验数据吻合得不好。根据热力学优化的结果，他认为1273K 时不存在B2 相的溶解度间隙，且只会在低温时才存在。2009年Zhu 等[20]利用平衡合金法制备了一系列样品，主要研究的是三相区的相边界，对于B2 相是否存在溶解度间隙的问题，通过第一性原理计算了0K 时Ni–Al 和Al–Ru 体系中B2 相的形成焓，并利用这些数据进行热力学模型参数的优化，优化后的计算相图显示1473K 时存在B2 相溶解度间隙，在1523K 时溶解度间隙消失。2009年Raghavan[21]总结了相关研究结果，尤其评估了Chakravorty[15–16]以及Zhu[20]等的试验相图数据，得出结论，在1273K 时出现了范围很小的β1+β2的溶解度间隙，当温度升高到1523K 时，溶解度间隙消失，相图上出现了连续的B2 固溶体相。

试验材料与方法

原材料为质量分数99.995% Ni、99.999% Al 和99.95% Ru。其中Ni为厚约1mm 的板材，Al 为薄片材，Ru 为粒状。采用分析天平（精度为0.1mg）称重，进行合金成分配比。随后，采用WK–Ⅱ型电弧感应熔炼炉在氩气保护下进行熔炼将其合金化。为了尽可能消除成分偏析，合金质量控制在20g 以下，且翻转重复熔炼5 次以上。对于高熔点难熔金属Ru，尽量延长每次熔炼的时间。将熔炼后的纽扣锭封入氩气保护的石英管中密封，置于1473K 的马弗炉中保温3d 后水淬，进一步消除成分偏析，提高合金的成分均匀性。

本研究主要对富Ni 端的相图进行验证，不在富Al 区域设计试验。并采用合金法与扩散偶法相结合的方法对相平衡进行测定。

1 扩散偶样品的制备

将均匀化后的试样线切割为4mm×4mm×4mm 的块状，然后用超声波清洗去除油污并进行表面磨抛处理至镜面，以保证制作扩散偶时具有良好的接触面。采用纯钼夹具将样品夹紧，再将扩散偶试样密封在氩气保护的石英管中，分别在1273K中保温15d，1473K 中保温7d，具体试验方案如表1 所示。试样从高温马弗炉中取出后水淬，磨抛清洗后采用JXA–8230 型EPMA 测定成分，样品成分测试误差为±0.5%。

2 合金法样品的制备

均匀化后的试样用线切割成合适的大小后，用抛光机将切割后残留的油污以及氧化层打磨干净，将样品封入氩气保护的石英管中密封，分别在1273K 的高温炉中保 温45d，1473K 保 温30d，具体试验方案如表2 所示。试样从高温马弗炉中取出后水淬，磨抛清洗后采 用Sigma–300 型能谱仪（Energy dispersive spectroscopy，EDS）测试处理好的样品中各相的成分，成分测试误差为±2%。

热力学模型

1 溶体相模型

本研究在描述溶体相φ（包括liquid、fcc、bcc 及hcp 相）时使用的摩尔Gibbs 自由能的表达式[7]为：

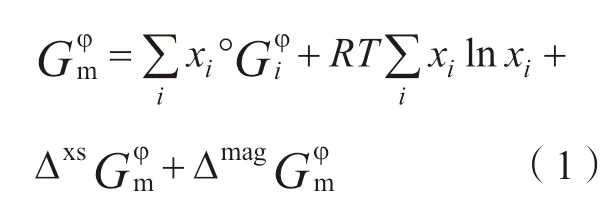
其中，xi（i=Ni，Al，Ru）表示元素i的摩尔分数；R为气体常数；T为绝对温度。°Gφi表示非磁性状态下结构为φ 相时元素i的摩尔Gibbs 自由能，数据来自Dinsdale[22]的SGTE数据库，表示为：

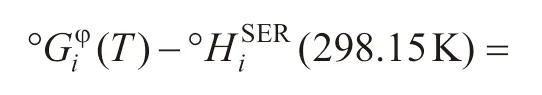
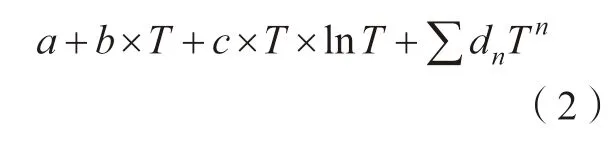
ΔxsGφm是过剩Gibbs 自由能，表示为：

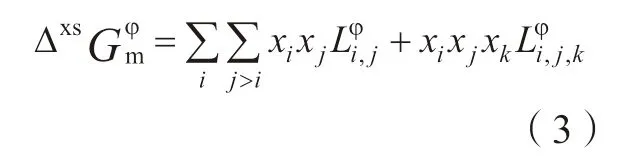
其中，Lφ表示二元系或三元的交互作用参数；ΔmagGφm表示φ 相发生磁性转变时Gibbs 自由能的变化值。

2 亚点阵模型

亚点阵模型可以用来描述含间隙原子溶体相、金属间化合物和化学计量相等。对于A–B–C 三元系，若θ 相被描述为（A，B）P（A，C）Q，则表示第1 个亚点阵含有组元A 和B，第2 个亚点阵含有组元A 和C，点阵比例为P∶Q。该相的摩尔Gibbs 自由能表示为[23]：

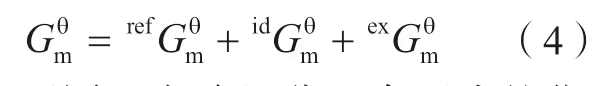
不同亚点阵组分组合而成的化合物（APAQ、APCQ、BPAQ、BPCQ）被称为端际化合物，θ 相的Gibbs 自由能由基于端际化合物所构成的能量参考面、理想混合能和超额自由能所构成，分别表示为：

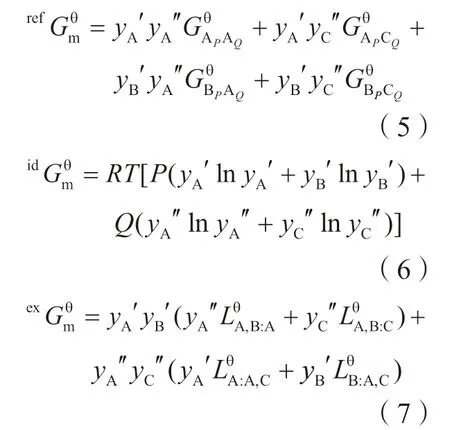
其中，y′A和y′B表示第1 个亚点阵中组元A 和B 的点阵分数，y″A和y″C第2 个亚点阵中组元A 和C 的点阵分数。

端际化合物的Gibbs 自由能，以APCQ为例，可以表达为：

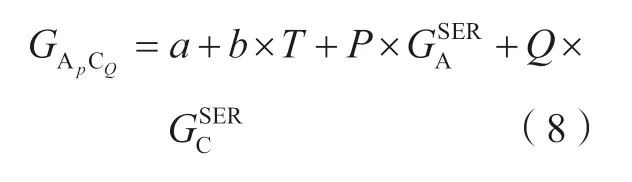
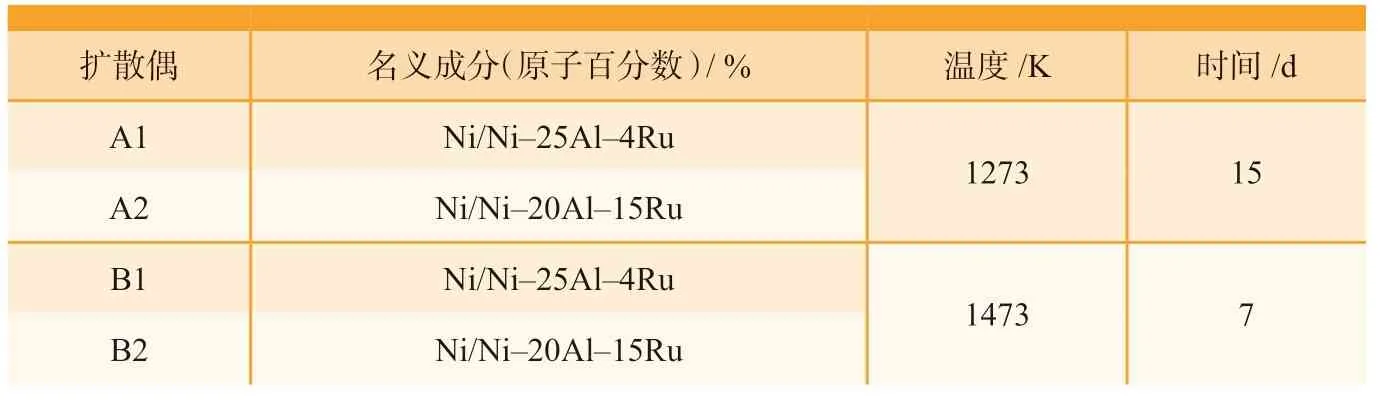
表1 扩散偶及试验条件Table 1 Diffusion couples and experimental conditions

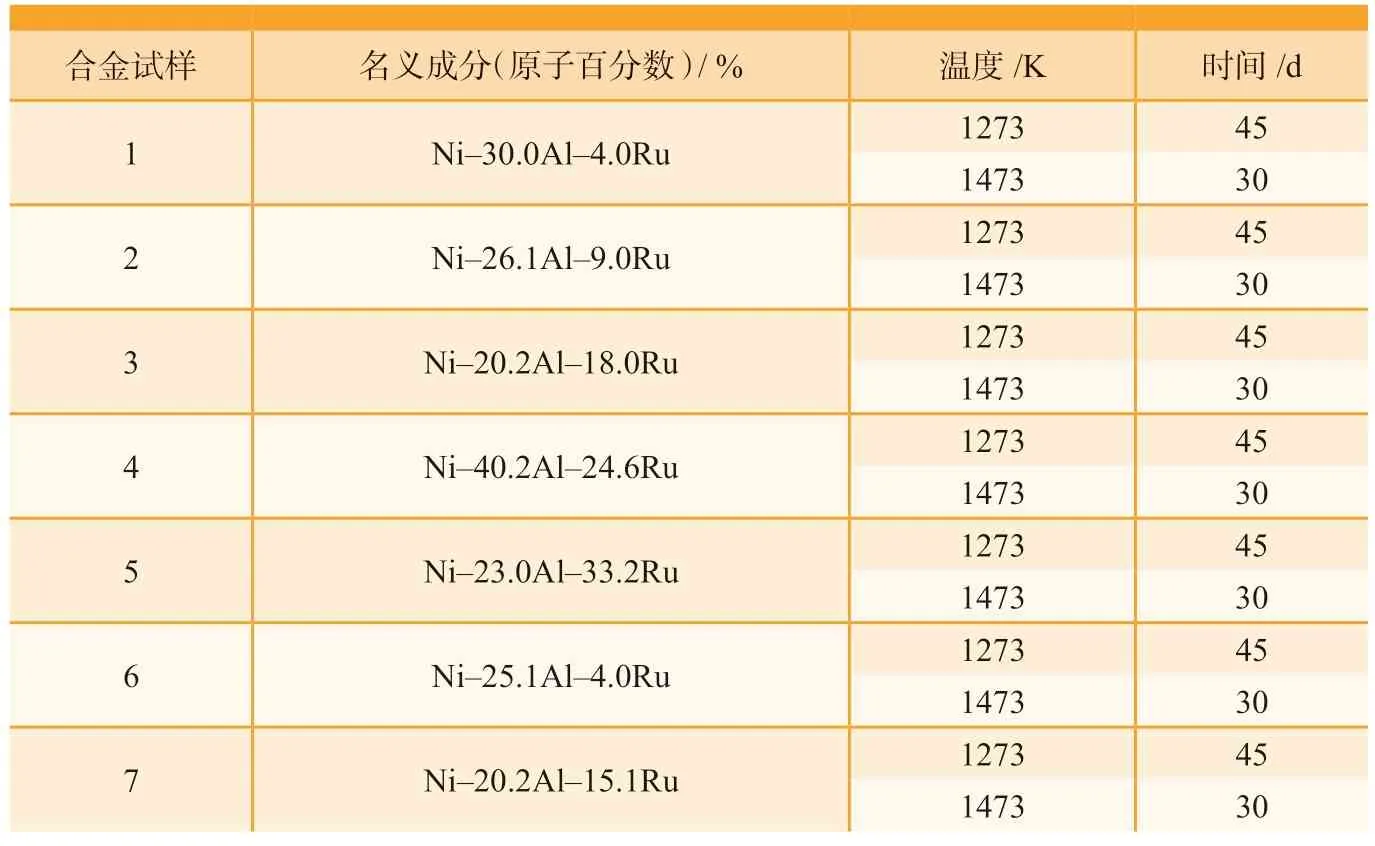
表2 合金试样成分及试验条件Table 2 Alloy compositions and experimental conditions

其中，和分别表示A、C在298.15K 和一个大气压下元素稳定相参考态（SER）的Gibbs 自由能，a表示APCQ的形成焓， 为形成熵对Gibbs 自由能的贡献。

3 有序–无序模型

有序–无序模型用一个Gibbs自由能表达式描述有序相和无序相，其关系式为[7]：

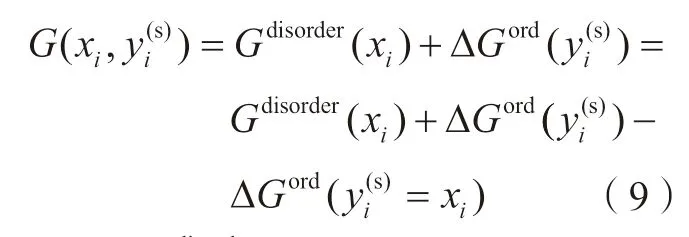
其中，Gdisorder(xi) 是无序溶体相的Gibbs 自由能，而ΔGord(yi(s))表示晶格有序对自由能的贡献。当亚点阵中点阵分数相同时，即yi(s)=xi，晶体处于完全无序状态，ΔGord(yi(s))=0；当点阵分数不等时，晶格为有序性状态， ΔGord(yi(s))≠0。

本研究中对基于fcc 和bcc 的有序/无序相采用了有序–无序模型。2009年Zhu 等[20]描述Ni–Al–Ru 三元系的B2 相时，热力学模型为（Al，Ni，Ru）0.5（Ni，Ru，Va）0.5。考虑到B2 相晶体结构的对称性，本研究将所有元素包括空位放入亚点阵中。另外，Zhu等[20]在描述bcc 有序无序相时将赋值为0，而本研究采用了王杨[7]评估之后给出的值，即=30T。

第一性原理计算

本研究运用第一性原理计算方法来计算面心立方（fcc）和密排六方（hcp）结构的Ni–Ru 二元无序固溶体在0K 下的混合焓。首先构建反映合金元素随机分布特性的特殊准随机结 构（Special quasirandom structure，SQS）模型[24]。然后基于密度泛函理 论[25]（Density functional theory，DFT），运用VASP（Vienna ab initio simulation package）程序计算NiRu 二元fcc 和hcp 无序固溶体在0K 的总能量。第一性原理计算结果经过转换后获得混合焓，具体公式如下：

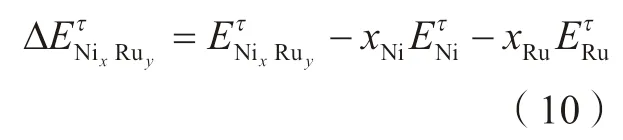
其中，xNi和xRu分别代表Ni和Ru的摩尔分数；EτNixRuy为第一性原理计算获得的NixRuy合金在τ（τ= fcc 或hcp）相结构下的总能量；EτNi和EτRu分别为第一性原理计算获得的纯Ni和纯Ru 的总能量；ΔEτNixRuy是NixRuy合金的混合焓。

在第一性原理计算过程中采用缀加投影平面波[26–27]（Projector augmented–wave，PAW）赝势法，平面波截断能取400eV。采用Perdew等[28]提出的广度梯度近似 （GGA–PW91）表述交互关联泛函。利用Monkhorst–Pack 包[29]构造布里渊区k点网格。对于fcc 相，k点的总数乘以单胞的原子个数至少为7200；对于hcp 相，k点网格为11×11×7。利用SQS 方法产生无序结构，构建了16个原子的超胞，包括如下成分构型，即Ni1Ru15、Ni4Ru12、Ni8Ru8、Ni12Ru4和Ni15Ru1。超胞结构完全弛豫，弛豫后采用四面体法进行校正[30]，进行最终的静态计算。电子自洽和离子弛豫的收敛标准分别为10–5eV/unit cell 和10–4eV/unit cell，以确保能量收敛到至少1meV/unit cell，并进行自旋磁化计算。使用ZenGen 脚本工具[31]，在VASP 计算过程中自动生成输入文件。

结果与讨论

1 Ni–Ru 二元系

本研究重新优化了Ni–Ru 二元系fcc 和hcp 的模型参数。由于Ni–Ru 二元系缺少热化学数据，故以第一性原理计算的0K 时fcc 和hcp 相的混合焓作为优化时的依据。为了尽可能保证拟合相图数据，在优化时对VASP 计算的混合焓设置了较低的权重。

图1 为不同参考态下优化和SQS计算得到的fcc 和hcp 相混合焓的比较（其中虚线表示Hallström 等[12]优化计算的混合焓曲线，实线为根据优化后的参数计算的fcc 和hcp 的混合焓曲线）。由于在非稳定相区弛豫有可能导致结构不稳定，故本研究仅拟合稳定相区的SQS 数据，即fcc和hcp 相分别拟合富Ni 端和富Ru端的两个数据。

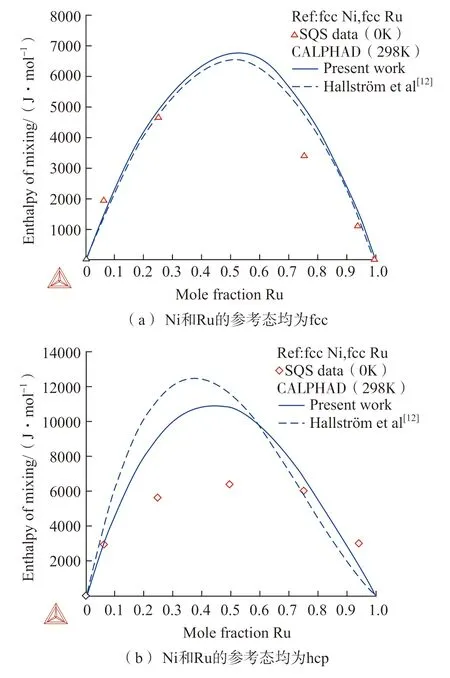
图1 Ni–Ru 二元系不同参考态下优化和SQS 计算得到的fcc 和hcp 相混合焓的比较Fig.1 Calculated enthalpies of mixing for fcc and hcp in Ni–Ru binary in comparison with SQS results

Raub 等[8]测试结果显示，包晶反应发生时Ru 在fcc 和hcp 相中的固溶度原子百分数分别为29.7%和51.3%，但分析相图上的数据点，此时的温度约为1550℃，和其文中给出的1490℃不一致。Kornilov 等[10]制备的试样（即在1200℃、1000℃、900℃、800℃下分别退火24h、50h、100h、200h）在低温下很可能未达到平衡状态。Tryon 等[11]使用扩散偶法测相图的准确性较高，但其数据未公开发表，2004年Hallström[12]进 行Ni–Ru二元系的优化时引用了其数据，故本研究参考了Hallström 给出的数据。进行优化时，固相线的拟合主要参考了Raub[9]以及Tryon 等[11]两组试验信息，包晶反应数据的拟合主要参考Kornilov 等[10]的结果，液相线则参考了Raub[9]以及Kornilov 等[10]的试验结果。优化之后的计算相图与试验数据吻合较好（图2）。与Hallström等[13]优化的结果进行对比，可以发现计算的相边界在Ni 端与之基本吻合，但在Ru 端有一定差别。这是由于考虑了第一性原理计算的混合焓数据，对二元系相图的优化结果产生了影响。

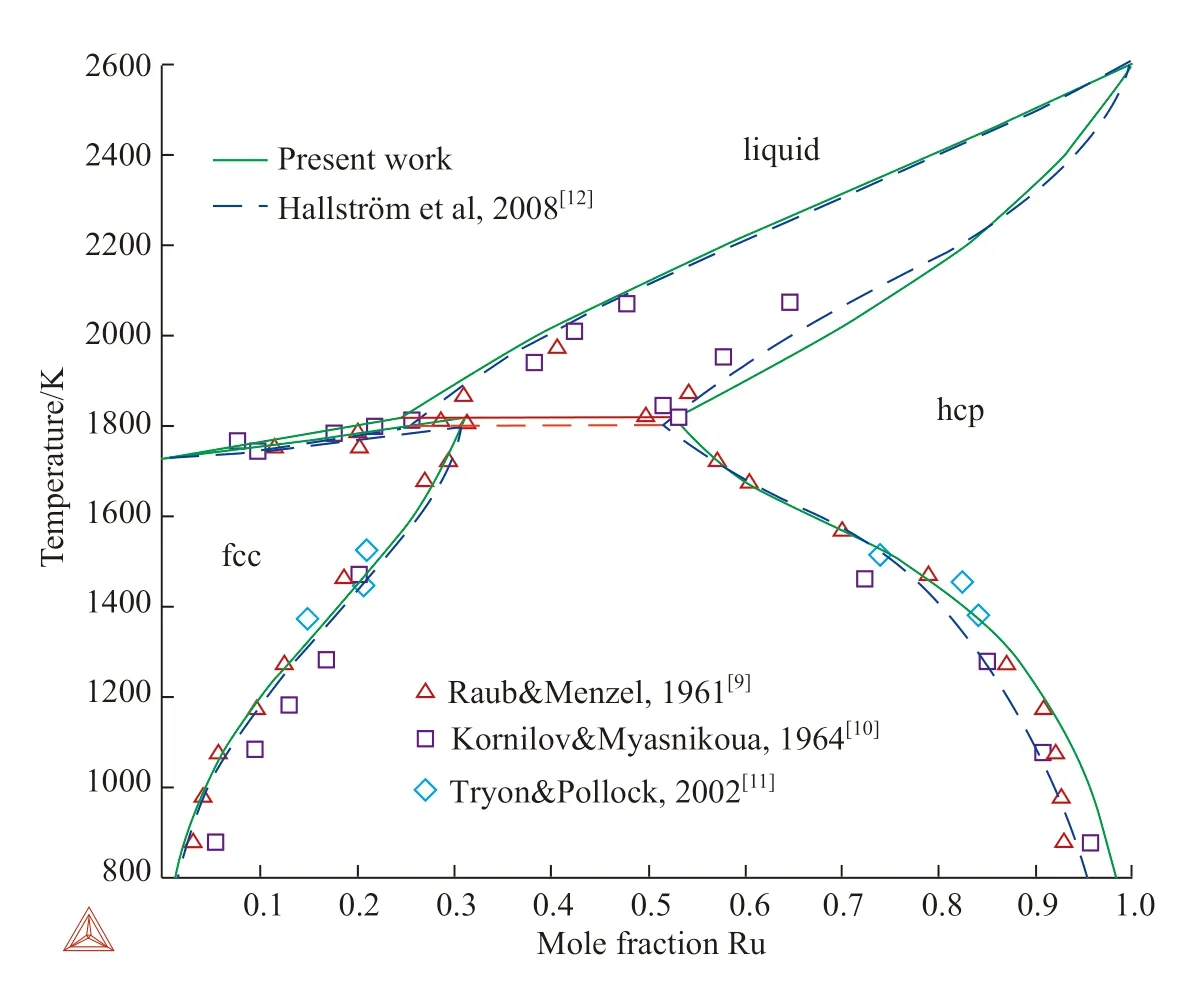
图2 本研究与他人计算的相图及试验数据的比较Fig.2 Comparison of calculated phase diagram by present work and others with experimental data

2 Ni–Al–Ru 三元系

2.1 试验结果

根据试验结果，Ni–Al–Ru 三元系相图在富Ni 端主要由γ、γ′、β1（B2–NiAl）、β2（B2–RuAl）和δ 的单相区，γ+β2、γ+γ′、γ′+β2、γ′+β1、β1+β2、β2+δ、γ+δ 两相区，以及γ′+β1+β2、γ+β2+δ、γ′+γ′+β2三相区构成。

图3 是不同试验条件下得到的扩散偶试样的背散射电子（BSE）图像。通过EPMA 方法对制备好的试样进行定量分析，以两相交界处为中点垂直界面打21 个点，使用Matlab程序对测试所得的一系列数据进行拟合，最终得到两共存平衡相的相成分，在相图上表现为两相区的tie–line，数据结果如表3 所示。图3（a）是A2 扩散偶样品局部放大的BSE图像，主要测定的是γ+β2和γ+δ 两相区的tie–line；图3（b）是B1 扩散偶样品局部放大的BSE 图像，主要测定的是γ+γ'、γ+β1和γ'+β1两相区的tie–line。

图3 不同试验条件下的扩散偶试样的BSE图像Fig.3 BSE images of diffusion couples under different experimental conditions

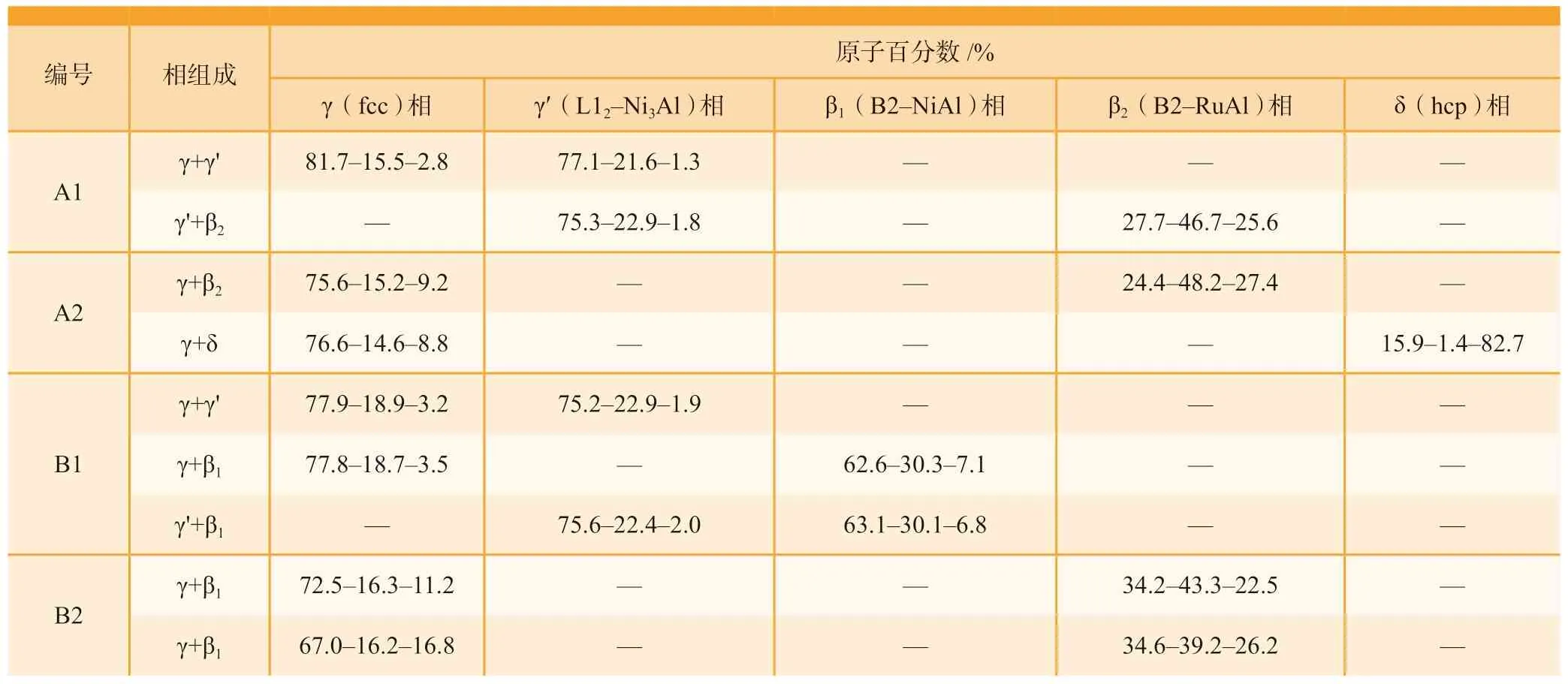
表3 EPMA 测定Ni–Al–Ru 三元系相平衡的结果Table 3 Measured phase equilibria results of Ni–Al–Ru ternary system by EPMA

图4 是不同试验条件下得到的平衡合金法试样的BSE 图像，通过EDS 方法对制备好的试样进行定量分析。测试所得的试验结果如表4所示。图4（a）是在1273K 下保温45d 的试验条件下1 号合金试样，其中灰色基体为γ′相，条状亮灰色为β2相；图4（b）是在1273K 下保温45d 的2 号合金试样，其中深灰色为γ′相，浅灰色为γ 相，白色为β2相；图4（c）是在1273K 下保温45d 的5 号合金试样，其中暗灰色为γ 相，灰色为β2相，亮白色为δ 相；图4 （d）是在1273K 下保温45d 的4 号合金试样，其中灰色为γ 相，白色为β2相；图4（e）是在1473K 下保温30d 的试验条件下6 号合金试样，其中灰色为γ′相，浅灰色为β1相；图4（f）是在1473K 下保温30d 的5 号合金试样，其中暗灰色为γ 相，灰色为β2相，亮白色为δ 相。

图4 Ni–Al–Ru 三元系典型合金试样的BSE 图像Fig.4 BSE images of typical Ni–Al–Ru ternary alloys

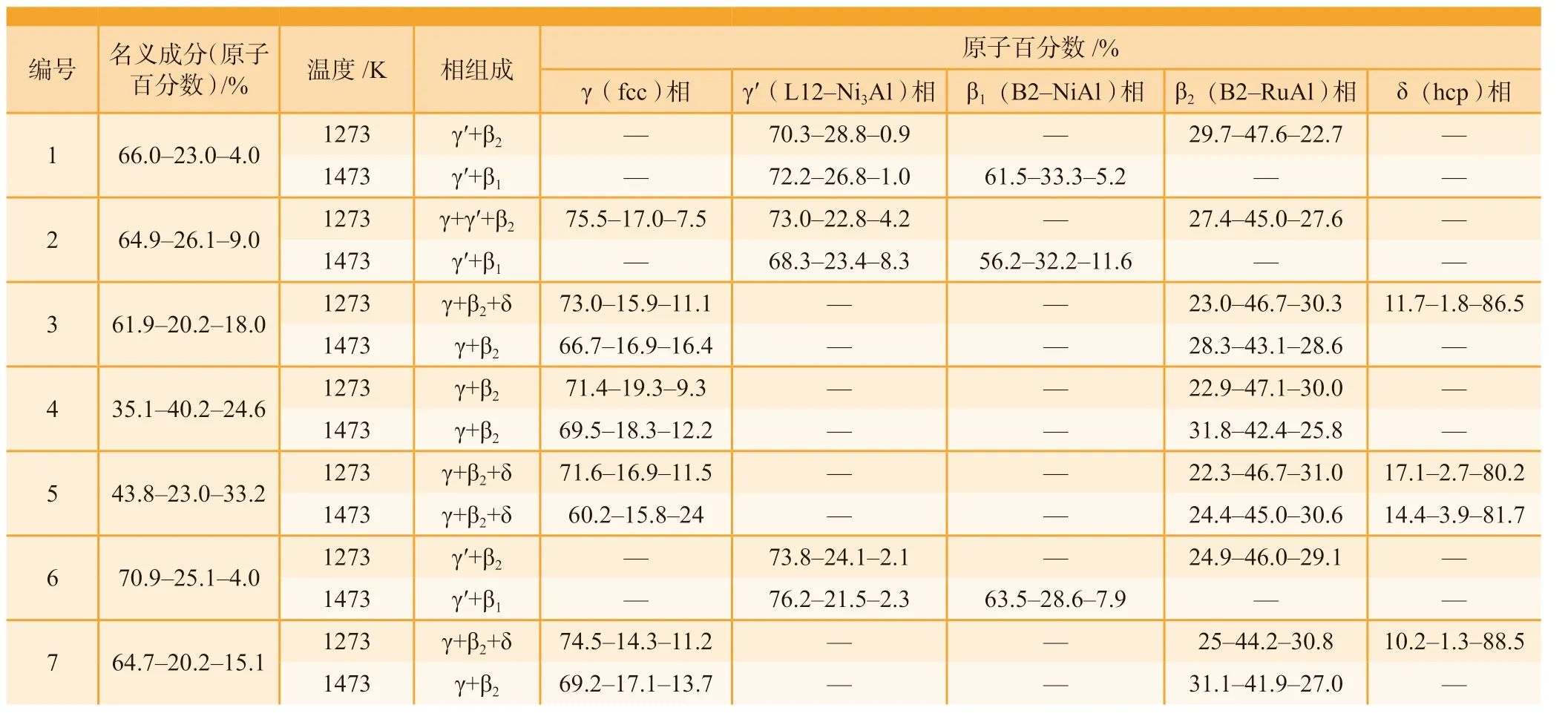
表4 EDS 测定的Ni–Al–Ru 三元系的平衡相成分Table 4 Measured phase equilibria of Ni–Al–Ru ternary system by EDS

本试验内容主要对两相区及三相区的相边界进行测定，同时验证前人试验数据的可靠性，所以在γ′+β2、γ+γ′+β2、γ+β2、γ+β2+δ 相区布置了试验点，测定了各相区平衡相的相组成和对应相成分，同时还通过扩散偶法测得了相图上γ+β2、γ′+β1、γ+δ 等相边界的位置。试验结果表明，合金法与扩散偶法的数据比较一致，证明了得到的试验数据的可靠性。如图5中所示，试验结果用黑色符号表示，其中虚线表示为平衡合金法的测试结果，点线为扩散偶法得到的试验结果。可以发现，合金法样品的试验结果与文献[14，20]中的相图数据更接近，且数据更丰富，所以在优化时尽量拟合了合金法样品测试得到的

数据结果。

2.2 CALPHAD 优化

Ni–Al–Ru 三元系的晶体结构和热力学模型如表5 所示，优化之后的模型参数如表6 所示。

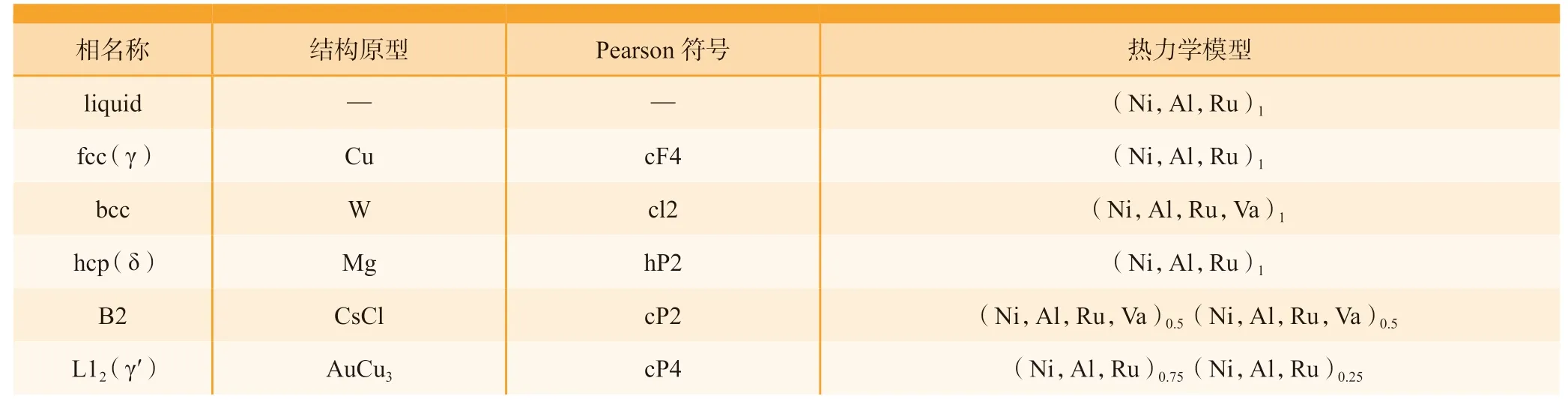
表5 Ni–Al–Ru 三元系各相的晶体结构和热力学模型Table 5 Crystal structures and thermodynamic models of phases in Ni–Al–Ru ternary system

表6 Ni–Al–Ru 三元系优化后的热力学模型参数Table 6 Assessed thermodynamic parameters of Ni–Al–Ru ternary system

在对Ni–Al–Ru三元系进行优化时，L12 和B2 有序相的端际化合物不是稳定相，缺少试验数据，故在进行热力学描述时使用了第一性原理计算值。Hallström 等[12]计算的L12 结构的亚稳相Al3Ru 和AlRu3的形成焓分别为–39.580kJ/mol 和 –5.69kJ/mol，而Zhu 等[20]给出的值分 别 为0.06kJ/mol 和–35.7kJ/mol，两组计算结果不一致。结合纯组元的第一性原理计算值，认为Zhu等[20]的工作可能混淆了Al3Ru 和AlRu3的计算结果，所以主要考虑Hallström 等[13]的计算结果。

与文献中试验数据相比，1273K的试验结果与Chakravorty 等[14]的工作结果比较符合，与Zhu 等[20]的试验数据也比较一致，所以在对1273K 的等温截面进行优化时考虑了前者相图试验数据。1473K 的等温截面在优化时只考虑了本研究测得的试验数据，而1523K 的等温截面在优化时主要拟合Chakravorty 和West 的试验数据。在对3 个温度下的等温截面进行优化后结果如图5所示，计算结果与试验数据吻合度较高。另外，本研究还使用优化后的热力学参数计算了1273K 时的等温截面，与Tryon 等[19]报道的试验数据也基本吻合，如图6 所示。

图5 CALPHAD 优化计算的Ni–Al–Ru 三元系不同温度下等温截面与试验数据的比较Fig.5 Calculated isothermal sections of Ni–Al–Ru ternary system in comparison with experimental data

图6 优化计算的Ni–Al–Ru 三元系1273K 等温截面与他人试验数据的对比Fig.6 Calculated isothermal section of Ni–Al–Ru ternary system at 1273K in comparison with experimental data by others

结论

（1）评估了Ni–Al–Ru 有关的3个二元系的相图优化结果，并结合第一性原理计算的混合焓数据对Ni–Ru 二元体系重新进行了优化，得到了可靠的二元系模型参数。

（2）采用合金法和扩散偶法，借助SEM 和EPMA 测定了Ni–Al–Ru 三元系1273K 和1473K 时的等温截面。

（3）结合晶体结构数据和第一性原理计算结果对三元系的各相进行热力学描述，在对前人的优化和试验工作做了综合评估后，主要对Ni–Al–Ru 三元系1273K 和1473K 时的等温截面进行了CALPHAD 优化。

（4）优化后的计算相图与试验数据基本吻合，得到了一套可靠自洽的模型参数。