基于重构曲面的整体叶盘叶根过渡区域精确搭接加工轨迹生成方法*

2021-10-15李世军王文理

航空制造技术 2021年18期

朱燏，李世军，王文理

（1.中国航空制造技术研究院，北京 100024；2. 复杂构件数控加工工艺及装备北京市重点实验室，北京 100024；3. 数字化制造技术航空科技重点实验室，北京 100024）

航空发动机的整体叶盘的叶片采用五轴数控铣削的方式进行加工[1]。首先选用曲率半径较大的刀具完成除叶片叶根附近区域以外的叶片中上侧区域的加工，然后使用与叶根圆角半径相同的小直径球头刀铣削叶片叶根过渡区域。

叶片叶根过渡区域是指在叶片曲面上靠近叶根圆角的一段区域，该区域内叶片曲面的uv参数线与叶根圆角边界线相交，难以通过传统的轨迹规划方式生成光滑渐变的加工轨迹[2]。现阶段，叶根过渡区域的加工通常采用球头刀具进行点铣，并通过偏置清根轨迹来生成过渡区域的加工轨迹。对于清根加工轨迹，蔡永林等[3]在保持刀具与流道面和叶片面同时相切的情况下计算加工轨迹的刀尖径矢与刀轴矢量，并生成无干涉加工轨迹。刘长明等[4]在计算理论余量的基础上识别需清根的区域并生成加工轨迹。西北工业大学相关学者在基于点搜索技术的基础上，提出了一系列的清根轨迹计算方法，搜索出叶根圆角边界点并生成加工轨迹[5–8]。Ren 等[9]通过一组虚拟球确定清根区域边界以及刀具的切触点，进而生成清根加工轨迹。此外，对于复杂曲面的侧铣加工，Gong 等[10]提出的基于约束面的轨迹计算方法与Li 等[11]提出的球头锥鼓型刀具的轨迹生成算法都可生成加工叶根过渡区域的加工轨迹。然而，提出上述的清根加工轨迹生成算法的目的是加工叶根圆角，在叶根过渡区域的加工中，未考虑与相邻加工轨迹之间的搭接问题。

在精确搭接轨迹生成方面，贺英等[12]通过调整刀轨驱动线的位置使圆环面刀具加工复杂曲面时的参数边界落在有效搭接区间内，进而实现加工轨迹的搭接。金曼等[13]通过控制圆环面刀具的端点误差生成具有重复搭接区域的加工轨迹。Xu 等[14]针对圆环面刀具端铣自由曲面提出双驱动线算法与Zhu 等[15]针对鼓形刀具侧铣自由曲面提出的双点接触算法也可以生成具有搭接效果的加工轨迹。然而这些方法生成的加工轨迹实现的是一次生成的多行加工轨迹之间的搭接，而非多次生成的不同加工轨迹之间的搭接。对于一次生成的多行轨迹，上述算法为了实现不同行轨迹之间的搭接，需要在每行轨迹计算的同时，计算该行轨迹对应的加工区域的边界，进而通过加工区域边界的搭接实现相邻两行轨迹之间的搭接。但是在目前算法和商用软件中，为了保持不同轨迹计算操作之间的独立性和高效性，并不生成某一轨迹计算操作对应的加工区域的边界，并且在执行某一个轨迹计算操作时不对其他轨迹计算操作的结果进行引用或参考，因此无法直接实现相邻轨迹之间的精确搭接。对于某些专用的叶片、叶盘加工编程软件或编程模块，在虚参数化功能的支持下，可附带实现相邻的球头刀螺旋加工轨迹之间的搭接，但不能实现鼓形刀加工轨迹与球头刀加工轨迹之间的搭接；在这些软件中，若针对叶根过渡区域单独生成其他拓扑形式的轨迹，则不能与已生成的螺旋加工轨迹之间形成精确的搭接。其根本原因是没有识别并单独地划分出真实的叶根过渡区域，因而不能够单独地对该区域进行处理，并进而生成可搭接的加工轨迹。

在整体叶盘的叶片较短且叶片弯扭程度不大的情况下，可使用通用的CAM 软件（如UG NX 的叶盘叶片加工功能）或专用的CAM 软件（如Hypermill 等）计算加工叶片曲面的螺旋加工轨迹和平行加工轨迹。该功能在设置几何体的基础上，通过两种驱动方式规划叶片曲面的加工轨迹，一种是在叶肩面与流道面之间按比例插值生成轨迹，另一种是通过偏置流道面生成加工轨迹。但是，在流道面狭窄的情况下，该功能在叶根过渡区域处无法生成完整的加工轨迹，且加工轨迹的进刀点位置及刀轴矢量难以灵活控制。在目前的CAM软件中，叶根过渡区域的加工轨迹与叶身加工轨迹之间通常存在一定的重叠，重叠区域的叶片曲面将被重复切削，由于钛合金叶片加工中的回弹现象，重复切削区域的轮廓度一定会受到影响。由于航空发动机叶片的加工精度要求高，且叶片在加工中存在一定的变形，如果不能准确地搭接相邻区域的加工轨迹，极有可能导致叶片（尤其是叶片进排气边）的过切。此外，过多的重复切削也增加了不必要的加工轨迹，增加了零件的占机时间，影响了加工效率，增加了加工成本。因此，针对叶盘叶片加工过程中叶片上侧与叶根过渡区域使用不同刀具或不同方法进行加工时产生的轨迹搭接问题，本研究提出一种生成精确搭接加工轨迹的方法。通过读入已使用的加工轨迹，识别已加工区域与未加工区域，并在此基础上进行未加工区域的曲面重构，进而生成相应的加工轨迹。

本研究首先给出了整体叶盘叶身已加工区域的识别技术；其次使用识别的已加工区域边界线与叶根圆角边界线重构出相应的叶根过渡区域；然后针对重构的加工区域进行轨迹规划与生成；最后，通过对某压气机整体叶盘的叶根过渡区域的加工试验来验证本研究提出的相应算法的效果。

面向叶根过渡区域曲面重构的边界求解方法

整体叶盘在叶根圆角上侧的叶片曲面可分为已加工区域与叶根过渡区域两个部分，如图1 所示。已加工区域通常选用较大直径球头刀或具有复杂母线形状的鼓形刀具进行加工，叶根过渡区域通常采用小直径球头刀加工。

如图1 所示，叶根过渡区域在上边界与下边界两条曲线之间，其中上边界是已加工区域的边界，下边界是叶根圆角与叶身曲面相交的边界线。本研究首先通过对使用的加工轨迹进行分析，找到已加工区域的离散点集，进而找到已加工区域的边界作为叶根过渡区域的上边界。然后处理叶根圆角的边界线，确定叶根过渡区域的下边界，为重构叶根过渡区域的曲面奠定基础。

图1 整体叶盘叶根过渡区域Fig.1 Transitional surface of a blade on a blisk

1 已加工区域的离散点集求解

1.1 面向球头刀的已加工区域离散点集求解方法

通过分析已使用的加工轨迹确定对应的已加工区域。如图2 所示，对于任意需分析的加工轨迹所需的几何信息包括刀具尺寸、加工坐标系下的刀尖径矢PMα、加工坐标系下的刀轴矢量TMα、加工坐标系OMe1e2e3，刀尖径矢是刀具坐标系的原点在加工坐标系下的位置。工件坐标系由坐标系原点OW与3 个正交单位矢量[XW，YW，ZW]构成，加工坐标系是工件坐标系下的某一特定坐标系且与加工轨迹的计算、输出直接相关，加工坐标系在工件坐标系里的坐标原点为OM，各轴坐标为e1、e2、e3，记矩阵MMW=[e1，e2，e3]。则工件坐标系下的刀尖径矢PWα与刀轴矢量TWα可由式（1）解得。

在使用球头刀加工叶盘叶片时，任意刀位处的刀心点的位置OTC如式（2）所示。叶片曲面上距OTC点最近的点为PC，且||OTCPC|| =R，即PC点为该刀位的切触点。加工轨迹中所有刀位的切触点PC，组成点集{PS}，该点集即为已加工区域的离散点集。

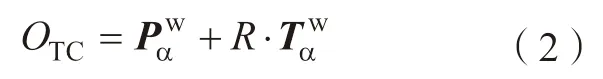
1.2 面向鼓形刀的已加工区域离散点集求解方法

图2 球头刀加工中使用的离散点Fig.2 Sample point selected for a ball-end cutter

在使用鼓形刀具加工自由曲面时，由于刀具本身的几何特点，使其具有较大的行宽，因而相应的加工区域的边界点将远离刀具的切触点。为此，在已知加工轨迹的情况下，首先确定任意刀位的特征线，随后在特征线上寻找满足残高的左右边界点，两个边界点之间的点将用于表征已加工的区域。

如图3 所示，在任意刀位的刀尖点建立刀具坐标系OTXTYTZT，其中ZT为刀轴矢量T Wα 的单位矢量，令本刀位的刀尖径矢到下一个刀位的刀尖径矢的方向为ey=PWαPWθ+1，则XT=（ey×ZT）/‖ey×ZT‖，YT由XT与ZT的矢量叉乘确定。由于已知刀具轨迹，工件坐标系下刀具上任意一点Q的速度τWα可通过刀尖点的速度VWT与刀具旋转的角速度wWT进行计算，如式（3）所示。

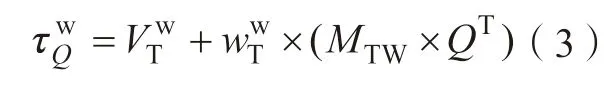
其中，MTW为刀具坐标系在工件坐标系下的位置；QT为刀具坐标系下刀具面上Q点的位置。QT通过参数h与θ定义，h为刀具坐标系下点沿ZT的值，θ为点绕ZT的旋转角度，同样求解出该点在工件坐标系下的法矢nWQ=MTW·nTQ。

若点Q满足式（4）所示约束，则点Q为该刀位处的特征点，点Q在刀具运动后形成的包络面上。任意刀位处的所有特征点的集合构成该刀位处的特征线，代表了该刀位处所形成的加工面的真实状态。

如图4 所示，对于第i个刀位点，使用纬线圆法离散鼓形刀的轮廓面，每个纬线圆上对应的特征点向曲面求最近距离，鼓形刀在瞬时运动速度下形成的特征线上存在两个边界点PCL与PCR，PCL与PCR点与理论曲面之间的最近距离等于预设的残高ε，PCL与PCR之间的纬线圆上解得的特征点构成第i个刀位点的加工区域点集{PSi}。如式（5）所示，全部n个刀位点的点集的并集记为{PS}，{PS}用于表征已加工区域。

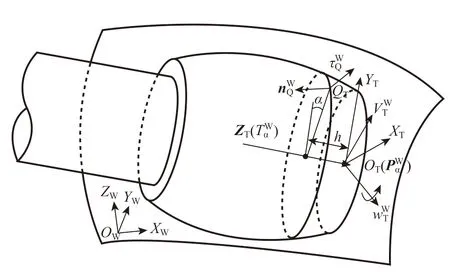
图3 鼓形刀加工自由曲面的几何关系Fig.3 Relationship between a barrel cutter and a sculptured surface

图4 鼓形刀加工中使用的离散点Fig.4 Sample point selected for a barrel cutter

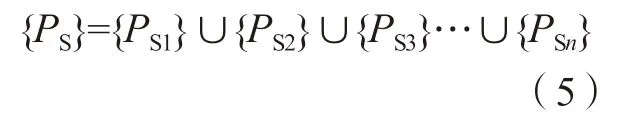
2 叶根过渡区域上边界求解

在获得点集{PS}的基础上，需要识别出点集的边界作为已加工的区域的边界，进而在后续的轨迹规划中实现对已加工区域的搭接。由于点云的形状并不规则，点集并不一定是一个凸集，因此使用传统的三角剖分方法将无法获得有效边界。本研究针对叶片加工需求，在uv参数空间内使用基于包围盒的边界搜索算法寻找点集{PS}所代表的已加工区域。在搜索点集{PS}的边界的过程中，只需要寻找点集{PS}沿叶展方向的下侧边界，不需要寻找点集{PS}内的孔与上侧边界。

图5 所示为使用文献[16]中所述边界搜索算法对边界点搜索后得到的结果。该搜索算法用于寻找uv参数域内的边界点。将边界点顺次连接后，得到一条由多段线组成的边界线。该边界线光顺性差，不能直接用来重构加工区域或规划加工轨迹。为了保证加工边界的光顺性，本研究在此基础上采用NURBS 曲线对边界点进行插值，但直接插值后的曲线可能会超出原多段线边界的范围。

为了保证提取的区域边界都在多段线边界内，从而保证后续生成的加工轨迹与已加工的区域之间的精确搭接效果，需在插值生成边界曲线的基础上对曲线进行调整。本研究首先遍历多段线边界中的每一段，计算每段中插值边界超出多段线边界的距离Δv；然后将该段边界线左右的点在参数域内向上移动Δv，作为新的边界点；最后重新插值生成边界线。若新生成的插值边界线仍然有图5 所示现象，则继续执行此过程，直至插值后生成的NURBS 边界曲线都在多段线边界内部为止。生成的已加工区域边界如图6 所示，该边界是参数空间内的已加工区域的边界，其对应的三维空间内的曲线即是叶根过渡区域的上边界。

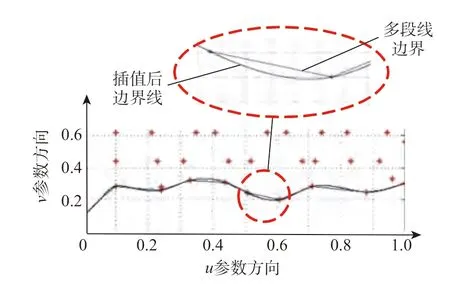
图5 已加工区域边界曲线构造Fig.5 Constructing boundary for a machined surface

图6 加工区域边界曲线调整Fig.6 Adjusting boundary for a machined surface

3 叶根过渡区域的下边界处理方法

叶根过渡区域的下边界是叶根圆角的边界线，下边界曲线与上边界曲线之间通常不具备统一的参数对应关系。如图7 所示，为了避免重构的叶根过渡区域曲面的褶皱，首先将叶根过渡区域的上边界与下边界曲线进行对齐。首先通过前一节求解出的上边界CBU（t）来重生成下边界CBD（t），并使叶片曲面∑B上的点PBUi与点PBDi在叶片的弦长方向（参数u方向）上具有相同的参数值，其中PBUi=CBU（ti），PBDi=CBD（ti），ti∈{t0，t1，…，tn}。

对于图7 所示的叶片模型，叶片沿叶展方向为参数v方向。首先采用等误差法将上边界CBU（t）离散为n个采样点PBUi，i∈[1，n]，误差值为δ；其次对于每个采样点，计算通过该点的等u线；然后求解等u线与原始叶根圆角∑C的交点PBDi；最后通过插值n个PBDi点重构下边界曲线。对于重构的下边界曲线CBD（t），计算其与原始的叶根圆角边界线CBD0之间的最大偏差dt，若dt小于预设值ε则采用此重构曲线作为边界，否则通过系数ξ减小δ的值，并重新执行此过程，如图8 所示。

图7 加工区域边界寻找叶根圆角边界上的点Fig.7 Finding points in boundary of a fillet corner which corresponds to points in boundary for a machined surface

叶根过渡区域曲面重构与加工轨迹规划

图8 叶根圆角边界曲线重构流程图Fig.8 Flow chart for reconstructing boundary of a fillet corner

在曲线CBU（t）与曲线CBD（t）的基础上，对叶根过渡区域进行重构，为了控制重构的曲面与原始曲面之间的偏差，可在曲线CBU（t）与曲线CBD（t）之间插入m条过渡曲线。如图9 所示，为曲线CBU（t）的采样点PBUi在uv参数域内对应的点，为对应的曲线CBD（t）上的点PBDi在uv参数域内的点。首先在uv参数域内计算点之间的m个插值点，然后计算相应插值点对应的工件坐标系下的点，遍历完曲线CBU（t）上的n个采样点后，得到m组过渡点，每组n个点。在此基础上生成的三维空间内的m组过渡曲线如图10 所示。根据自由曲面建模理论[17]及方法[18]，在m条曲线的基础上采用曲线串插值的方法生成重构的叶根过渡区域。由于此过渡区域的上边界是已加工区域的边界，下边界是叶根圆角边界，因此按照新生成的曲面规划的加工轨迹可实现与已加工区域的搭接且光滑地在两个边界之间过渡。

图9 uv 参数域内的过渡曲线Fig.9 Transitional curves in uv–parametric region

针对重构的叶根过渡区域，可采用球头刀或球头锥鼓形刀具进行加工，并采用等参数的方式规划加工轨迹，加工轨迹沿重构的过渡区域的参数u方向，从而生成由已加工区域边界逐渐过渡至重构叶根边界的加工轨迹，如图11 所示。

本研究所述方法的核心是构造过渡区域的曲面，过渡曲面构造后，可生成螺旋加工轨迹或按等参数方式生成等参数轨迹。在叶片较短或流道空间较开敞的情况下，可采用螺旋加工轨迹。在叶片弯扭情况复杂、流道空间狭小的情况下，应当分区生成等参数的加工轨迹，使刀具从叶盘叶片的侧面进刀完成叶根过渡区域的加工。

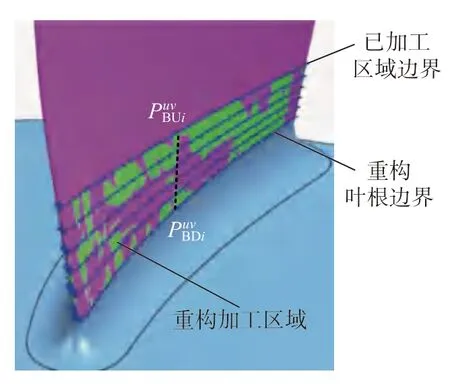
图10 基于过渡曲线的曲面重构Fig.10 Reconstructing a surface with a group of transitional curves

图11 重构曲面的加工轨迹生成Fig.11 Tool path generation with a reconstruction surface

整体叶盘流道空间极其复杂，叶片叶根区域在排气边附近的径向流面角小，整个叶片沿发动机轴向的径向流面角变化幅度大，叶根过渡区域扭曲程度大，因而难以生成通用的螺旋加工轨迹。本研究所述方法正是针对此类叶盘在实际加工中的工艺需求而设计的轨迹生成算法，在重构叶根过渡曲面后，分区域计算等参数加工轨迹，从叶盘叶片的进气侧或排气侧进刀，针对叶根过渡曲面扭曲较大的区域单独生成加工轨迹，进而完成相应区域的加工。

重构曲面上的点与原始设计曲面之间沿设计曲面的法向存在一定的偏差，该偏差值在远小于曲面的轮廓度公差的情况下可采用本方法直接加工重构曲面。目前，整体叶盘中叶片曲面轮廓度要求最高的区域为叶片进气边，为了保证加工后该区域的轮廓度，根据加工经验应当控制重构曲面与设计曲面之间的最大偏差值小于该轮廓度的1/10。通常对于航空发动机的叶盘叶片来说，此时重构曲面与原始曲面之间的偏差值已远小于使用机床的RTCP 精度，因而忽略曲面的理论偏差对加工后精度的影响。

重构的曲面通常不与原始曲面相切，在曲面光顺程度要求较高时，可将重构曲面作为驱动曲面，将原始叶片曲面作为加工曲面计算轨迹，从而保证加工后的叶根区域与已加工区域之间具有更好的搭接效果。后续的研究中也可通过相关方法[19]调整重构后曲面的控制顶点及节点矢量来调整重构曲面，使其与原始曲面之间在边界处达到G1 连续，从而进一步保证该区域的光顺性。

实例

通过某压气机叶盘叶根过渡区域的加工来验证算法的可行性。整体叶盘的叶片模型如图12 所示，其叶片下侧通过一个R2.5mm 的圆角与流道面相连，叶片高60mm，相邻叶片之间的最近距离12.1mm，叶片与加工刀具之间易产生干涉。

图12 整体叶盘模型Fig.12 A blisk model

使用传统的CAM 软件生成螺旋加工轨迹加工叶片叶身中上侧，加工中采用φ10 的球头刀。由于刀具的刀头半径大于叶根圆角的半径，因而该刀具加工后将在叶片上留下未加工的区域。为此，首先采用本研究方法读入已生成的加工轨迹，得到加工区域的点集{PS}，并判断已加工区域的边界如图13 所示。

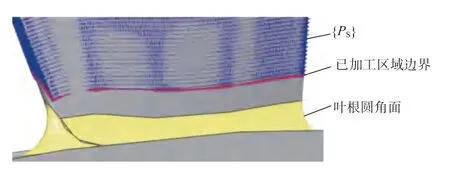
图13 已加工区域边界识别Fig.13 Boundary recognition for a machined surface

图14 为使用本研究算法重构的加工区域及生成的加工轨迹。在获取已加工区域边界曲线的基础上，首先生成参数对齐的加工区域上下边界曲线，随后在其内部插入3 条曲线，最后通过这5 条曲线重新生成由已加工区域边界至叶根圆角的叶根过渡区域。该区域将用于分区生成加工轨迹，并使用直径φ5 的球头刀具进行加工，加工后该区域的效果如图15 所示。可知，使用重构的叶根过渡区域计算的加工轨迹，可实现叶根过渡区域与叶片中上侧已加工的区域之间的光滑搭接，并实现该区域与叶根圆角之间的光滑过渡。如图16（a）所示，按等参数的方式从重构叶根区域上均匀取出2000 个点（40 行×50 个/行），依据微分几何原理[20]计算点到原始叶片曲面之间的法向距离，得到的法向偏差的最大值为0.000548mm。叶根过渡区域在加工后通过三坐标测量机的REVO测头及相关软件进行了扫描测量与评价，叶片在该区域的截面线轮廓度合格，如图16（b）所示。

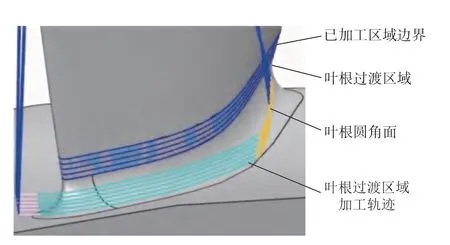
图14 按本研究方法重构叶根过渡区域与生成轨迹Fig.14 Surface reconstruction and tool path generation for a transitional surface using presented method

图15 过渡区域加工效果Fig.15 Machining result for a transitional surface

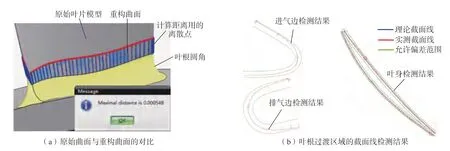
图16 叶根过渡区域曲面重构及加工结果Fig.16 Surface reconstruction result and machining result of blade root transitional surface

图17（a）为用原始叶片曲面规划的加工轨迹，由于叶根未加工区域的参数边界在参数v方向有较大的波动，在使用原始曲面规划加工轨迹时，为了覆盖整个未加工区域，需要根据未加工区域边界在参数v方向的最大值与最小值来确定轨迹规划时使用的参数边界。由于在通常情况下叶片类零件的uv参数方向与叶根圆角的边界不平行，规划的加工轨迹将覆盖大量的重复切削区域，而且会造成加工轨迹与叶根圆角边界相交的情况。生成的加工轨迹如图17 （b）所示，在保证加工轨迹不过切叶根圆角面与流道面的情况下，生成的加工轨迹无法实现向叶根圆角边界的渐变过渡，进而生成了多条被干涉检查面（叶根圆角面）裁剪的加工轨迹，增加了空走刀与重复走刀的情况，降低了加工效率，且无法保证叶根圆角的加工质量。