基于近似熵的摇号系统随机性安全检测研究

许颖媚 匡碧琴

（1．广东省高性能计算重点实验室，广东 广州 510000；2．广东省计算技术应用研究所，广东 广州 510000）

1 引言

随着信息化的发展，摇号系统的应用范围无处不在。摇号上学系统、抽奖摇号系统、保障性住房摇号、新车上牌摇号等都是以公平性为基础保障电子政务的公信力。摇号系统的公平性需要从技术角度进行验证。

从技术角度看，摇号系统的公平性取决于随机数发生器生成的随机序列。随机序列在信息安全领域用来增强安全性[1]，因此随机性的质量直接影响摇号系统的安全问题。随机性分为3类：统计学伪随机性、密码学安全伪随机性、真随机性。统计学安全伪随机性基于统计学的概念，定义为在生成的随机比特流序列中“1”出现的频率和“0”出现的频率一致。密码学安全伪随机性基于密码学的概念，定义为通过给定随机序列的随机生成算法和一部分序列不能推算出随机序列的剩余部分。真随机性基于物理现象产生，其随机序列是不可重现的。基于上述定义，生成的随机序列分为真随机序列和伪随机序列。真随机序列可通过硬件使用电子元件的噪音生成，对技术要求比较高。伪随机序列由计算机的随机函数和种子产生，满足统计学/密码学安全伪随机性的定义标准。在某种程度上，伪随机序列是可以通过标准方法进行检测的。而实际应用中，摇号系统的随机数就是伪随机序列。对摇号系统的伪随机序列进行检测可验证随机序列的质量[2]。

对摇号系统的检测研究中，文献[3,4]采用基于插值多项式的可验证随机数生成方案实现摇号系统的公平性检测。该检测方法满足可参与性、可验证性的要求，但该方法从用户是否参与随机数的生成过程进行验证，前提是在用户需要验证的情况下去验证。而摇号系统的使用往往是先通过第三方检测再进行摇号，因此上述方法不利于实际使用。文献[5]运用独立同分布的中心极限定理配合历史的双色球开奖数据验证彩票的随机性，该方法通过分析大量的历史数据采用X2-分布检验，不适用于摇号系统单次使用的随机性检测。目前国际上通用的检测方法是将多种随机性检测算法组成检测套件，文献[6]采用NIST统计测试套件进行检测并在套件的机上实现优化以此提升运算速率。近年来，近似熵检测成为我国的随机性检测标准之一。因此，本文将近似熵应用在电子摇号系统的随机性检测中，并以某区公办小学电脑摇号系统为例说明近似熵检测方法对摇号随机数的可验证性，保证摇号系统的公平性与安全性。

2 摇号系统随机数的构造

摇号系统的随机数通常由随机函数种子生成。种子是生成伪随机数的初始使用值，生成的机制是将种子的值通过一定算法转化为随机数空间中的某个点，依次产生的伪机数均匀分布在这个空间中。因此采用相同的随机函数生成器和种子会产生可预测的随机数。通常随机函数是给定的，摇号系统要保证生成的随机序列具备不可预测性需要保证种子本身具备随机性和不可预测性。所以实际使用中，摇号系统以当前时间为种子，保证前向不可预测性和后向不可预测性，即通过已生成的序列无法预测后续的输出序列，也无法得出种子。摇号系统的随机数区间则根据摇号规模自由制定。

3 近似熵检测

随机数的检测可依据国家密码管理局标准GM/T 0005-2012和NIST测试标准。近似熵检测作为GM/T 0005-2012中的一种统计检测项目，判断依据是分析待检测序列是否具有较强的规则性，适用于摇号系统随机序列的不规则性分析。近似熵检测的原理是通过比较m位可重叠子序列模式的频数和m+1位可重叠子序列模式的频数来判定随机性[7]。假设模式，则Yi(m)在待检测序列中出现的相对频数为：，=π，πi表示l=(i1,i2,…,im)在待检测序列中出现的相对频率。其中，近似熵检测对参数n和m的要求为：m＜-2。整体算法过程如下：

（1）将二元序列ε的前m-1位数据添加到序列末尾形成新序列ε'，则新序列ε'长度为n'=n+m-1。

（2）计算新序列ε'中的所有2m个m位子序列模式出现的频数vi1i2…im，针对所有的j(0≤j≤2m-1)计算。

（4）用m+1替换m重复步骤（1）到（3）获得计算后的φ(m+1)。

（5）计算熵ApEn(m) =φ(m)-φ(m+1)，ApEn(m)的值越大表示检测序列具有不规则性和不连续性；反之，值越小表示检测序列具有规则性和连续性。

（6）计算统计值V=2n[ln2-ApEn(m)]。

（7）最后计算度量指标p-value的值，计算公式为：p-value=igamc，其中igamc表示不完全伽马函数（Incomplete Gamma Function），将度量指标p-value与显著性水平α进行比较，依据标准α设为0.01，若p-value≥α，则认为通过近似熵检测；否则，不通过检测。

近似熵检测参数m的取值参考标准应为m=2,5，检测时需将随机序列转化为二元序列，二元序列是指由“0”和“1”组成的比特串，并计算m和m+1的重叠子序列出现的频数来检测随机性。

4 基于近似熵的摇号系统随机数检测

对摇号系统的检测实际是对摇号系统生成的伪随机数采用近似熵进行检测。摇号系统将随机函数生成的随机数作为派位号。本文以某区公办小学电脑摇号系统为例，阐述摇号系统通过近似熵检测验证随机数的公平性与安全性以及基于随机数的摇号过程。该摇号系统采用数据库管理数据，通过对数据库访问获取需要摇号的学生和学校数据，随机数的生成服务于摇号过程，验证模块与摇号模块相互独立以保证耦合性，其服务架构如图1所示。

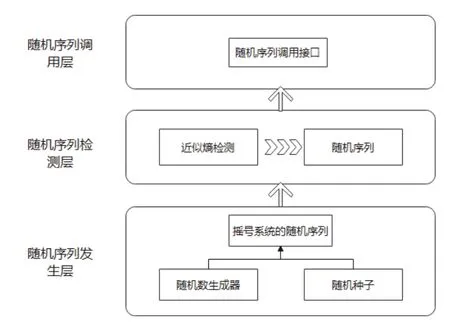
图1 随机序列服务架构

在摇号系统生成伪随机序列后，将伪随机序列转化为二元序列进入验证模块进行近似熵检测，通过近似熵检测则进入摇号过程，未通过检测则退出系统，流程如图2所示。

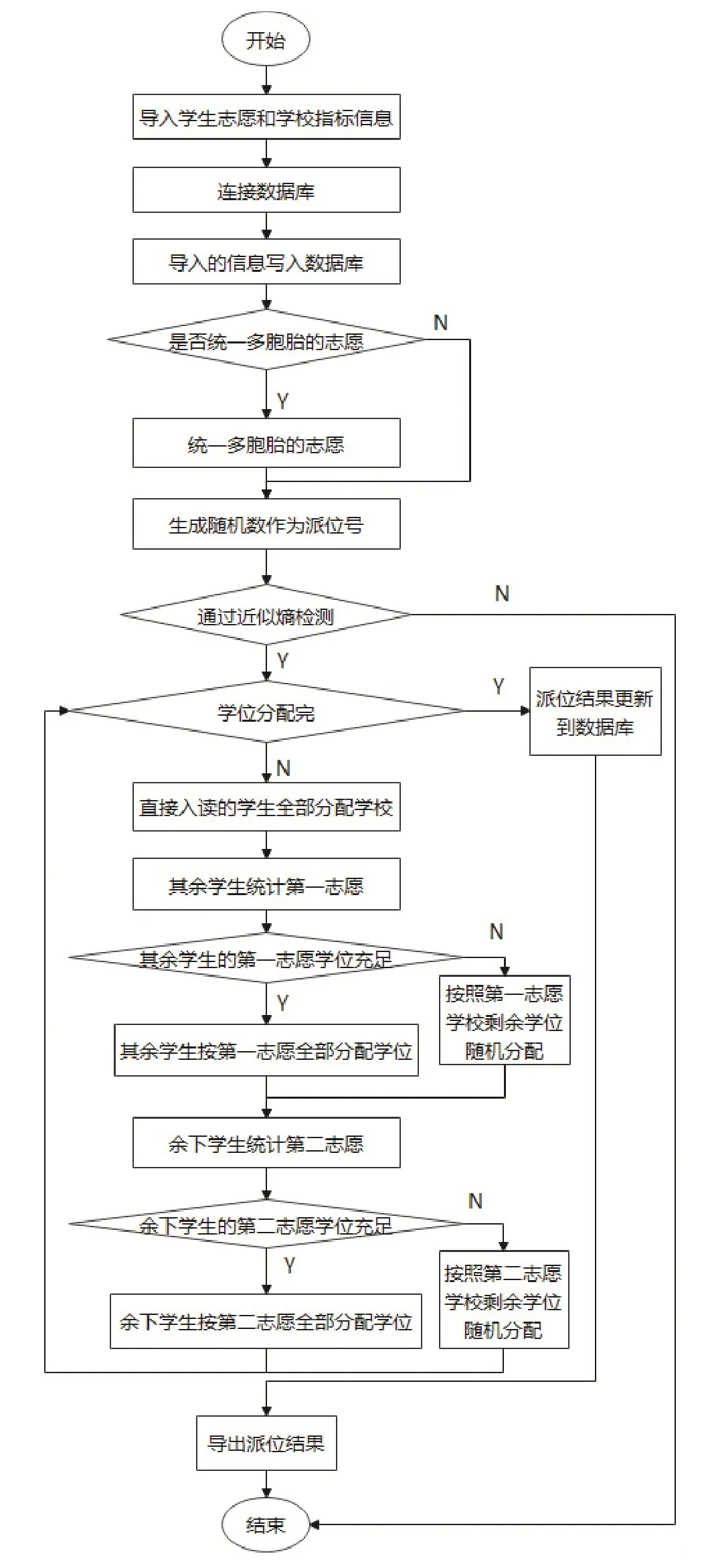
图2 近似熵检测和摇号过程

本文按照近似熵检测代码思想，分别以序列长度n=100、200为样本规模，样本数据为某区公办小学电脑摇号系统随机函数生成的随机序列转化的等价二元序列。实验参数取m=2,5进行计算，所有的算法过程在Windows系统采用python实现。实验结果如表1所示，表明摇号系统的随机数通过了近似熵检测，说明摇号系统的随机数具备可验证性。

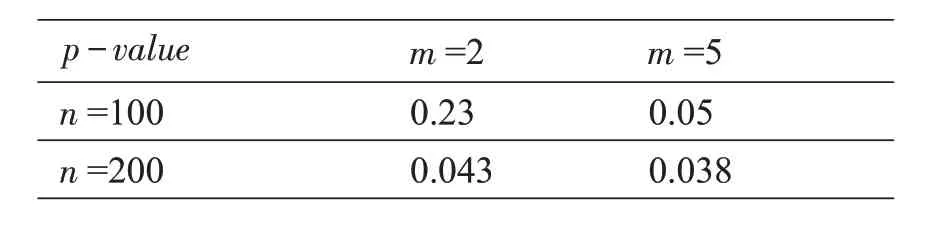
表1 近似熵检测结果

5 结语

本文基于近似熵检测法验证摇号系统生成的随机数，并以某区公办小学电脑摇号系统为例阐述近似熵检测法在摇号系统中的使用过程。实验结果表明摇号系统随机数具备可验证性、随机性和不可预测性，为保障摇号系统的公平性和安全性提供理论基础。随机性检测标准中还有其他检测项，下一步的主要工作将是研究适用于摇号系统大量随机序列检测的高效算法。