数学思想方法在课堂教学中的应用

钮丹媛

摘 要：数学课程标准要求义务教育阶段教师要充分发挥自己在课堂中的主导作用，让学生在课堂中获得所需的数学知识和数学技能、在学习中学会数学思想和方法，培养学生良好的逻辑思维。因此，教师需要把数学思想及方法巧妙地渗透到日常的课堂教学中，让学生在课堂中体会数学思想和方法的存在，学会使用它们。

关键词：一元一次不等式 数形结合 类比 归纳 转化

随着数字时代的到来，数学的培养目标不再是单纯地传授的数学知识，而是让学生理解、运用所学知识，重在培养学生逻辑思维。然而数学思想方法需要长期的培养，因此在数学知识跨度较大的初中，想让学生较好地掌握数学思想方法，就需要教师把理论知识作为基础，把课堂作为途径，将数学思想方法渗透到课堂中，在教学过程中潜移默化地影响给学生。本文就苏教版初中七年级“一元一次不等式”一节课中的教学片断，就教师如何渗透数学思想这一点与大家交流分享。

1 课堂片段

1.1 新课引入

师：观察以下式子，找出其中的不等式？这些不等式有什么共同特点？

（1）2x -2.5=15 （2）2x -2.5≥15

（3）x=4 （4）x<4

师：根据我们根据一元二次方程的定义可以明确左边两个方程所满足的条件。而右边三个不等式也满足这些特点。因此，我们可以得到一元一次不等式的概念：只含有一个未知数，并且未知数的次数为1，系数不等于0的不等式叫一元一次不等式。

【设计意图】在这个过程中，教师先复习一元一次方程，通过将方程与不等式进行比较，帮助学生发现两者的相同点和不同点，再根据一元一次方程的概念进行归纳，从而总结出什么是一元一次不等式。该过程中，教师运用了类比思想和归纳思想，由旧到新，这样能更好地帮助学生理解一元一次不等式。

1.2 例题讲解

师：解一元一次方程 3x+70=100

生：移项 3x=100-70

合并同类项 3x=30

系数化为1 x=10

师：由于一元一次方程和一元一次不等式的相似性，根据解方程的过程，结合不等式的基本性质解不等式，步骤有：

移项

合并同类项

系数化为1

师：解不等式14-2x>6，并把它的解集表示在数轴上，请同学上来作答

师：两位同学结果不一样，是哪位同学做错了，错在哪里？

生3：第一位同学做错了，第三步的时候，不等号两边同时除以-4，要改变不等号方向

师：我们看到在解不等式的过程中，在最后一步系数化为1时，我们一定考虑到系数的正负，根据不等式的基本性质，当系数为正数的时候，不等号不需要改变符号，当系数为负数时，不等号方向要需要改变。

【设计意图】此处教师首先复习了如何解一元一次方程，通过两者间的相似性，结合不等式的基本性质，引导学生解一元一次不等式。随后让学生自行解题，帮助学生自行发现错误，并即时总结易错点，强调了不等式性质的运用。同时，在教学过程中，将数轴与不等式联系起来，引导学生把数与图像结合，方便接下来教学。

1.3 拓展延伸

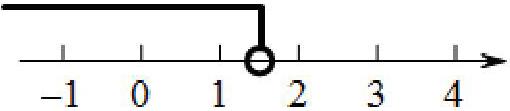
若关于x的不等式的正整数解有且只有1，借助数轴求a得取值范围

师：我们可以解得不等式的解集为，接下来如何来判断a的范围

生1：通过画数轴，我发现a要大于1，解集才能取到1。

师：还有其他的要求吗

生1：因为只能取1，所以取不到2，a要比2小

师：所以得到a的范围是，有没有其他意见

生2：a可以等于2，因为当的时候，解集为，正整数解还是只有1

师：那可以等于1吗？

生2：不可以，如果，解集是，这时候没有正整数解。

师：所以我们最后得到a的范围是

【设计意图】通过本题，将解不等式解集与数轴结合，通过运用数轴来确定解集的整数解。教师通过数形结合，帮助学生进一步理解数轴的使用方法。同时，运用了猜测的方法来考虑和这两种情况是否符合条件。

2 如何让数学思想渗透到课堂中

2.1 结合已有知识，活用类比归纳

数学知识间的联系紧密，教师在讲述一个新知识时，要以已学知识作为基础，适当地帮助学生复习旧知，并在此基础上再将新的知识融入进去。在这个过程中，教师可以通过类比及归纳等数学思想，通过比较，寻找新知识与旧知识间的联系与异同。在已有知识的基础上进行教学，减少学生对新学知识的迷茫感，让学生对要学的知识有所了解，这样能提高学生的好奇心、求知欲，学生才会愿意融入课堂。在教学过程中合理的运用归纳与总结的思想，方便学生理解知识，锻炼学生的逻辑思维，进一步影响学生的数学能力。

2.2 渗透转化思想，发散学生的思维

转化思想指的是将一个数学方面问题通过转化成其他问题来降低题目的难度和复杂度。而数学有一定的复杂性、灵活性，想要解决数学问题不能过于死板，要会变通，要尝试用多种方法去解决问题，而这就要求学生有较好的发散思维。

因此，在教学中，教师就需要渗透转化的思想，把学生新遇到的问题转化为熟悉的问题去解决，将复杂的问题转化成简单的问题。这就要求教师在教新知识时要善于引导学生发现新旧知识间的关系，帮学生找到两者间的联系。同时在解答难题时，仔细阅读题干，找到题目中显性或者隐性的各种条件，将复杂题目的解答分成几个阶段，降低解题难度。

2.3 优化解题过程，深化数形结合

数形结合思想作为数学思想方法中一个重要的部分。合理运用形的直观性，能使一个抽象的问题变得具体，从而帮助学生理解题目，还可以使解题过程更加简单化，解决很多的抽象问题。同时，数学知识涉及很多理论性较强的知识，对于学生而言，这些知识比较枯燥，很难提起兴趣。因此教师在教学过程中，要精准把握知识的特点，将知识点与图像紧密结合，将抽象概念转化为直观图像，方便学生更好地体会知识的迁移，让学生学会将数与形结合起来，将已学知识进行构建，形成自己能够理解的知识体系。这样就能在思维发展的过程中，通过数形结合这一思想，帮助学生更好地转换概念;培养学生的数感，发展学生的抽象思维能力。

3 总结

数学在初中阶段作为一个重要的学科，影响深远。数学的逻辑思维等能力也会影响学生的学习与生活的各个方面。因此，教师在教学过程中要重点强调对学生数学思想方法的教学，注重培养他们的逻辑思维能力。

参考文献：

[1] 严卿.借助情境渗透数学思想方法的基本策略[J].名師在线，2020，（32）：56-57.

[2] 邱明让.渗透数学思想方法培养数学学习能力[J].考试周刊，2020，（97）：91-92.

[3] 董明华.数学思想在初中数学解题中的应用研究[J].中学数学，2020，（22）：62-63.

[4] 陈富平.渗透数学思想方法培养逻辑思维能力[J].中学数学参考，2019，（27）：38-39.

[5] 祁慧.在数学教学中渗透思想方法培养学生能力的思考[J].中学课程辅导，2020，（01）：1.