基于知识要素平台 构建有效学习策略

张昌和

【摘要】有效教学关注每一个学习对象个体素质的高效发展，而课堂教学是否有效，能否获得高效，并不是看教师教的知识如何多，也不是看学生会做的作业有多少，更不能片面地理解为“用时少而教得多”或者说某某老师“教得认真，教得细致”;而是取决于单位时间内学生学会了什么，学到什么程度，掌握得好不好，学会学习了吗？基于小学数学分数（百分数）应用题的课堂教与学，谈谈构建有效学习的六点策略。

【关键词】基于  平台  构建  策略

【中图分类号】G623.5 【文献标识码】A 【文章编号】2095-3089（2021）07-0126-02

结构主义教学理论认为，任何一门学科都有一个基本结构，它反映了事物间的联系，包含了普遍而强有力的适应性。数学的抽象性、严密性和系统性决定了数学是一门可结构化教与学的科学。关于小学数学分数（百分数）应用题的教与学，结构化的探索有助于师生爱上课堂的教与学，提高课堂教学效率，提升教师教学水平。我们的数学课堂如何构建在有限的教学时间里培养学生的核心素养，让学生知识学得轻松、要点把握得牢靠、能力获得充分发展、取得满意的教学效果和实现预设的教学目标，是我们教育工作者为之思考和探究的重要课题，也符合新时代教育改革的方向。在小学数学教学中，分数应用题教学既是重点，又是难点，是小学阶段所应把握的核心内容。每到学习分数应用题这部分知识时总有那么一部分学生常常束手无策、摸不着头绪找不着北。现就小学数学分数（百分数）应用题的教与学，构建有效学习策略促进学生整体发展，谈谈有效学习的六点策略，以分散我们教与学的难点，帮助学生正确掌握解题策略，从而提高学生灵活解题的能力。

一、基于理解概念构建分数意义平台

分数的意义对于小学生来说是一个比较抽象的概念，理解“分数的意义”是小学生学习分数乘除法应用题的起点， “一个数乘以分数的意义”也是学生能否正确解答分数乘除法应用题的基础。怎样让学生理解单位“1”的含义？如何引导学生从具体的实例中逐步抽象、归纳出分数的意义就成了首先要解决的问题。学生在理解了意义后就为“求一个数的几分之几 （百分之几）是多少？”或“已知一个数的几分之几 （百分之几）是多少，求这个数”这两类分数应用题的解答做好了准备。因此，怎样让学生能准确理解掌握“分数的意义”和“一个数乘以分数的意义”就成了学好分数乘除法应用题的筑基工程，对此进行以下训练十分必要。

1.说一说，下面每句话中“分数”所表示的意义。

①六（2）班女生人数占全班的2/5;②今年比去年增产1/8;③一款手机降价1/7。

学生说：2/5表示把六（2）班人数平均分成5份，女生人数是2份;1/8表示把去年产量平均分成8份，增产的是1份;1/7表示把一款手机原价平均分成7份，降价的是1份。

2.议一议，下面每句话中“算式”所表示的意义

①“20×1/5” （表示“20的1/5是多少？”）;②“8千米×3/4” （表示“8千米的3/4是多少？”）;③“A×6/7”（表示“A的6/7是多少？”）

学源于思，思起于疑问。学生的数学思维常常伴随着对所接触学习素材的质疑而生，学生通过说一说、议一议，以“说”促思，用“议”释意。构建数学与生活的联系，在合作交流中体会，在理解构建中领悟单位“1”与“分率”的含义，为分数乘除法应用题的教与学迈出关键的第一步。

二、基于谁为“标准量”构建找对“分率”方法

“标准量”也就是“单位1的量”，如何正确找准“标准量” （单位“1”的量）和“比较量”（“分率”所对应的量），是小学生顺利解答分数乘除法应用题的关键。以北师大版数学为例，小学数学在二年级上册第六单元就出现了如“苹果有8个，桃子是苹果的2倍，桃子有多少个”“苹果有8个，苹果是桃子的2倍，桃子有多少个”这样的问题。尤其“苹果有8个，苹果是桃子的2倍，桃子有多少个”这一问题，学生的解题错误率不小于30%，这是一个困扰着小学数学一线教师的一大难题。如何把握“标准”，正确找对单位“1”和“分率”所代表的具体量呢？我认为关键要引导学生找出关键句和关键词，把握准关键句和关键词这一特征，学会对含“分率”的关键句的分析，能够准确而迅速地找出单位“1”的量和“分率”所对应的量，就能明确“量”“率”的关系。为此，可利用课前五分钟进行以下题型的练习。

1.找准单位“1”的量

例：画出下面句子中表示单位“1”的量。

①修了一條路的1/4;②一批水果，其中1/5是苹果;③高铁“复兴号”时速比“和谐号”时速提升1/6;④香菇脱水后，重量减少1/10。

2.理清“分率”所对应的量

例：修了一条路的1/4。

①一条路的（1/4）和（修了的）相对应;②一条路的（1-1/4）和（未修的）相对应。

虽然每节课只训练几道题，通过不断加强分数应用题找准单位“1”的量和理清“分率”所对应的量的基本结构模型的相关训练，有助于学生学会数学思维，推进学生学习的可持续发展。随着训练的持续积少成多，一段时间后，学生就能从中悟得一种数学能力。只要看到含有“分率”的“关键句”或“关键词”，就能把准“分率”的意义，从而实现为解答分数（百分数）应用题搭桥铺路之目的。

三、基于图文互动构建画线段图策略

苏霍姆林斯基说过：“教会学生把应用题‘画出来，其用意就在于保证由具体思维向抽象思维的过渡。”不同的学生对分数应用题有不同的理解，而且理解的程度还含有一定的特异性。通过画线段图可以把应用题中的条件和问题之间的关系清晰而直观地表示出来。所以在教学中，当学生感到对文字的理解有难度时，引导学生通过动手画线段图帮助自己理解数量关系，理清题意，也提高了自己分析问题和解决问题的能力。因此，要正确解答分数乘除法应用题，学会画线段图也是一种解题良策。

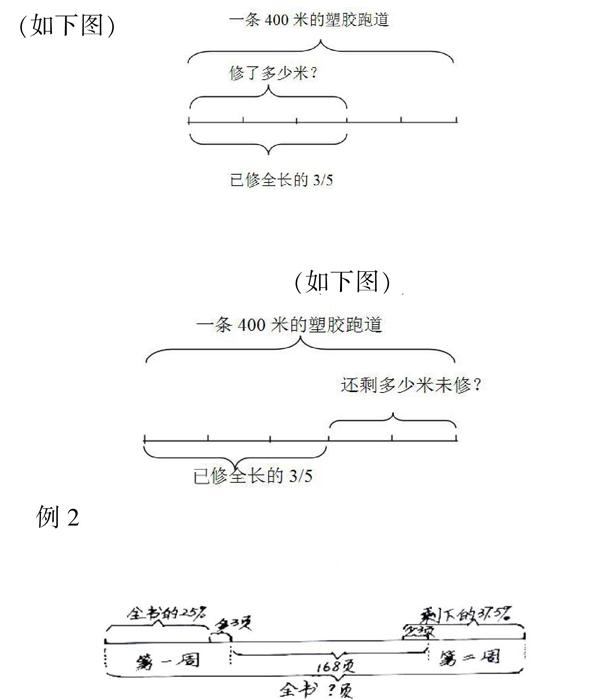
例1：学校修一条400米的塑胶跑道，已修全长的3/5，修了多少米？

指导学生画图三步骤：第一步先画标准量，也就是单位“1”的量;第二步再画比较量，也就是“分率”所对应的量;第三步标注已知条件和所求问题。 （如下图）

如果把问题“修了多少米”替换为“还剩多少米未修”那么这道题就转化为稍复杂的分数乘法应用题，掌握了画图步骤学生就能独立画出线段图。（如下图）

例2：笑笑看一本书，第一周看了全书的25%多3页，第二周看了剩下的37.5%还少3页，这本书还剩下168页没看，这本书有几页？

数学活动是学生认知的基础，解决问题的活动价值不局限于问题的解决，而在于让学生对问题的理解有自己的感受，能领会到解决问题的不同策略。如例2这道题既有数量的“多”和“少”，又存在以谁为标准的“单位1”的变换。如果单纯从文字上去理解，经过了小学阶段数学知识的积累能正确列式解题者还是屈指可数。若能将该题中的条件和问题用线段图表示，借助线段图的形象思维来支持抽象思维，“量”“率”关系一目了然了，正确解题也就得心应手了。

四、基于数量脉络构建写关系式模型

数学是关于“模型的科学”，小学数学分数应用题学习过程中的每一道习题都能从中找到其对应模型的影子，进行数学结构模型的训练能有效促进学生数学结构性思维，实现对数学素材的有效感知与获取。学生能否根据题意写数量关系式，是分数应用题正确列式的前提。有此基础，根据习题中的数量关系式学生就能列出相应的乘法算式或方程式，分数乘除法应用题就能迎刃而解。因此，构建写关系式这一模型就显得独具优势，小学数学教师要有计划地训练学生根据题中关键句写关系式。

例：1.一本书，看了1/5。

关系式：

（1）一本书×1/5=看了的;（2）一本书×（1-1/5）=未看的。

2.十月份用水量比九月份节约2/25。

关系式：

（1）九月份用水×（1-2/25）=十月份用水量;（2）九月份用水×2/25=十月份比九月份节约的用水量。

结构化的数学训练，有助于学生清晰、发散性地思考问题。学生通过例题这样的结构化训练能准确地写出乘法数量关系式，就为选择正确解题策略打好了基础，进一步提升用数学方式解决生活中的问题的能力。

五、基于思维拓展构建“分率”转化思想

分数应用题的数量关系复杂，变化大，比较抽象。关于“分率”的转化，不仅直接关系到学生的解题效果，而且对学生思维能力的拓展、知识面的延伸同样起着不可低估的作用。转化不仅是一种解决问题的策略，更是一种重要的数学思想，在解答一些复杂的分数应用题时，利用“分率”（百分率）的有关知识，将“分率”作适当的转化，可使题目的数量关系明朗，由间接变直接，由抽象变为具体，从而使问题得到顺利解决。同时，也掌握了多种解题的方法。

例：小百合合唱队男生人数是女生的2/3。通过分析我们可获得以下相关联信息：

（1）女生人数为单位“1”：男生人数是女生的2/3，男生人数比女生少1/3。（2）男生人数为单位“1”：女生人数是男生的3/2（3/2倍），女生人数比男生多1/2。（3）小百合合唱队人数为单位“1”：男生人数占全班的2/5，女生人数占全班的3/5，男生人数比女生人数少全班的1/5。

正如建构主义心理学家皮亚杰所言：“小学数学学习过程，就是通过不断的同化与顺应，实现数学认知结构不断平衡的动态过程。”通过“分率”的转化，不仅可以培养学生多思、多想的好习惯，还可帮助学生弄清知识间的联系。让学生感悟到转化的价值，学会了学习，还拓展了学生的数学思维空间，提升了学生的思维水平，同时又感悟到了运用转化思想选择最佳解法解决实际问题的数学魅力。

六、基于延伸对比构建分数应用题系统模型

小学数学新课标强调：小学数学知识的课堂教学，应该关注知识的结构和体系，着眼于知识的“生长点”与“延伸点”，更可以从多角度全方位去分析，从不同的层次有深度地去理解。为加深对不同类型、不同层次应用题的理解，我们可向教育对象提供对比练习素材进行思维训练。通过对比练习有益于知识结构的延伸，能清楚把握分数乘除法应用题间的典型特征，沟通知识间的内在联系，构建分数应用题知识系统模型，为学生快速、便捷、高效解答分数应用题打开通道。

例：淘气的书架分两层，上层有120本书，_______，下层有多少本书？

①下层是上层的4/5，列式：________;②上层是下层的4/5，列式：________;③下层比上层多1/4，列式：________;④上层比下层多1/4，列式：________;⑤下层比上层少1/5，列式：________;⑥上层比下层少1/5，列式：________。

通过上例逐步延伸对比训练，学生对分数应用题的解答就会逐步建立知识模型，系统掌握解题策略。可见，分数应用题的教与学，确有难度，但不是无法攻克的堡垒。有了延伸再辅以对比训练，所谓熟能生巧，只要我们遵循简单到复杂的认知规律，持之以恒、循序渐进，引领孩子走好求知路上的每一步，累积探究过程的点点收获，激励学生勇于探索、敢于攻坚，学好分数（百分数）应用题并非难事。

“教学有法，教无定法，贵在得法。”只要教师的“教”能激发学生的学习兴趣;学生的“学”有积极性、有动力;学习的过程有益于学生思维和创新能力的培养;学习的方法有助于知识的掌握和运用，都能称得上是教与学的好方法。有效的课堂教学作为一种理念，更是一种价值追求，一种教学实践模式，将会引起我们更多的思考、更多的关注，选择运用恰当的教学方法进行教学，为学生構建知识学习的模型，引领学生成为学习的主人、获取知识的主角，培养强烈的探求知识的欲望，高涨的学习热情，乐于学习，主动学习，学生学起来就有兴趣，就会有助于提高学习效率，为课堂搭建有效学习平台，切实提高课堂教学的有效性。