介子部分子分布函数的统计模型研究

谢修鹏，吕 准

(东南大学 物理学院，江苏 南京 211189)

量子统计方法,是一种量子力学和统计力学相结合形成的新的统计方法,在物理学的各个领域获得了大量的运用并取得很大成功.本文将讨论量子统计方法在粒子物理的运用,即确定强子的部分子分布函数.在介绍核子和π介子的部分子分布函数的统计模型基础上,将主要探讨如何利用现有实验数据来获取考虑K介子的部分子分布.

部分子分布函数是描述强子内部结构的一个重要的物理量，色禁闭导致很难从量子色动力学的拉格朗日量直接计算分布函数.因此从实验数据中利用参数化抽取分布函数成为了研究强子结构的重要途径.通常的参数化形式包括幂函数、多项式结合指数函数的形式，比如MSTW参数化[1]以及CTEQ参数化[2].近年来，一些新的方法也被用来研究部分子分布函数，统计模型方法[3]是其中一个代表性的方法.首先，在统计方法框架下，核子可以看成是一团给定温度下有限体积的、由不同部分子(夸克/反夸克和胶子)构成的处于平衡态的气体,因而具有清晰的物理意义.其次，夸克统计模型的基本元素是螺旋度(自旋在动量方向上投影)分别为+和-的夸克，其正确反映了微扰QCD 的手征特性.第三，统计模型具有很强的预言力，统计方法预言的深度非弹性散射结构函数和反夸克味道不对称性等结果均得到实验数据的证实.最后，统计方法需要的参数少，仅用几个参数就可以同时应用于非极化部分子分布和极化分布函数.基于上述优点，我们选择统计方法对K介子的分布函数进行研究.

统计方法同样可以用于研究介子部分子分布函数[3]. 显然，作为自旋为0的粒子，π介子的结构比自旋为1/2的核子结构简单得多. 对于核子，可以定义8个具有横向动量KT的夸克分布，在对KT进行积分之后，只剩下3个分布(非极化性、螺旋性、横向性). 而对于π介子，除了非极化性外，我们只能定义一个带KT的横向极化分布，其将在KT积分后消失.

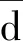
(1)

与在统计框架下构建核子的夸克分布一样，对于介子，也可以把初始能标下的夸克分布表示为两个简单表达式之和(Q=U，D)∶xQ(x)=xQ+(x)+xQ-(x)，其中

(2)

(3)

综上所述，轻夸克区的介子部分子分布函数是以10个参数进行参数化的，这种情况和核子十分相似.然而，10个参数中只有8个是自由参数，价夸克数守恒导致:

(4)

(5)

控制着小x行为的参数bG也取和核子相同的值，即bG=1.020. 而AG将由动量求和规则确定，即

(6)

文献[4]中利用式(3)和(5)构建的模型，以及约束条件式(4)和(6)，结合π-束流轰击钨靶的Drell-Yan双μ子产生的截面数据,对π介子分布函数进行了抽取，获得了相应统计模型的参数值.

类似的，可以利用上述统计模型来研究K介子的分布函数.NA3实验组[5]以K-介子作为束流轰击铂靶测量了K-N Drell-Yan过程，并测量了该过程的截面和π-N Drell-Yan过程的截面在不同x区域的比值.根据u夸克主导的原则，该比值近似于K-介子中u夸克分布和π-介子中u夸克分布的比值:

(7)

NA3实验组的结果显示,在大部分x区域，该比值小于1，特别是小x和大x区域. 这预示着K介子中u夸克的分布要小于π介子中u夸克的分布.

根据式(2)可以分别给出π介子和K介子的u价夸克的部分子分布函数:

(8)

(9)

图1 利用统计模型拟合K和π介子中u价夸克部分子分布函数的比值随x的变化(点为NA3实验数据[5]，竖条显示系统和统计误差，实线为最佳拟合曲线)

AUK=0.705±0.210，bUK=0.262±0.348

从图1的实验数据和拟合曲线的对比可以发现，统计模型可以很好地描述K和π介子参与的Drell-Yan过程的实验结果.利用抽取的结果，图2比较了K介子和π介子中u夸克的分布函数.其中误差条表示K介子分布函数的误差.可以发现，在小x区域，K介子中u夸克分布比π介子中u夸克分布小.其中，bUK>bUπ=0.048可以解释为何在小x区域UK(x)

图2 K介子中u价夸克部分子分布函数x*U(x)及相应误差条(虚线表示π介子中u夸克分布函数)

总之，本文将核子和π介子分布函数的统计模型方法运用于K介子分布函数的研究中.通过MINUIT最小化程序包，从介子-核子 Drell-Yan实验数据中抽取了K介子中u夸克分布函数统计模型的参数，发现统计模型可以很好地描述实验结果.这说明核子部分子分布函数的统计方法框架在介子范围内的推广是成功.同时，通过比较两种介子中u夸克的分布，发现K介子中u夸克的化学势小于π介子中u夸克的化学势.目前与K介子中部分子分布相关的实验和理论比较少，希望将来的实验能带来更多的信息，另外，希望统计模型能够更加完善，在获取介子的部分子分布函数和研究介子的内部结构方面取得成功.