若干delta势的薛定谔方程的傅里叶变换求解
2021-10-14熊路淋
熊路淋,谭 鑫,罗 光
(重庆师范大学 物理与电子工程学院,重庆 401331)
delta函数是一类重要函数,该函数描述的势在量子力学中也是一个非常重要的势.delta函数对应薛定谔方程的求解方法的讨论和研究也一直是学界的热门,而且求解一般仅涉及由于涉及单或者双delta势[1-3],讨论多delta势问题则相对较少.delta势约束下的薛定谔方程由于涉及分段问题以及相应的衔接条件,求解过程并不简单.特别是势的个数多时,薛定谔方程的求解过程更加繁琐[4-6].
针对量子力学中的傅里叶变换的讨论,一般在涉及坐标空间表象和动量空间表象中的关系时才给出.实际上傅里叶变换本身是一种比较有效的求解薛定谔方程的方法.但是由于傅里叶变换的条件较为苛刻,通过查阅傅里叶变换表[7-9]可知满足傅里叶变换的函数不多,因此在量子力学中用傅里叶变换法求解的实例不多,甚至并未真正提出这样一个求解方法[10-13].对于涉及双delta势阱、三delta势阱甚至n个delta势阱(即梳状delta势阱)的薛定谔方程,如果采用傅里叶变换法来求解,则求解过程将会变得相当简便.
本文研究基于傅里叶变换法求解若干delta势阱作用下定态薛定谔方程.
1 单delta势阱约束下傅里叶变换法求解
势V(x)约束下的定态薛定谔方程[3]为
(1)
当V(x)为delta势时,有
V(x)=-γδ(x)
(2)
这种情况下,薛定谔方程的常规求解一般需要从x≠0和x=0两种情况出发,得出对应的通解形式,然后利用|x|→∞时的边界条件以及x=0处的衔接条件,以确定相关的常数,最后得出特解和能级形式.但是如果采用傅里叶变换法求解,上述繁琐过程就可以大大简化.
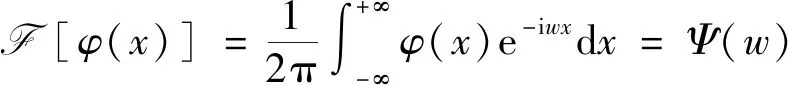

(3)
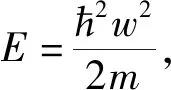
(4)
对式(4)作傅里叶逆变换,可以从以下3种情况进行分析
1)E>0:对式(4)两边作傅里叶逆变换,有
(5)
由于奇偶函数的傅里叶变换将保持函数的奇偶性的特点[14],式(5)得出的把函数也应该满足奇偶性,即φ(-x)=φ(x),故当x>0时
(6)
当x<0时
(7)
因此傅里叶逆变换结果为
(8)
进而得φ(0)=0,与前文矛盾,因此需舍去.
2)E=0:式(4)傅里叶逆变换表达式为
(9)
两边对x求导得
(10)
(11)
进而得
(12)
所以依然需要考虑保持被变换函数的偶函数性质φ(-x)=φ(x),因此
(13)
由于φ(x)有限要求φ(0)=0,与前文矛盾,因此需舍去.综合1)和2),下文就不再讨论E≥0,仅仅讨论E<0的情况.
3)E<0:式(4)傅里叶逆变换结果为[9]
(14)
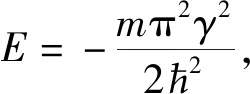
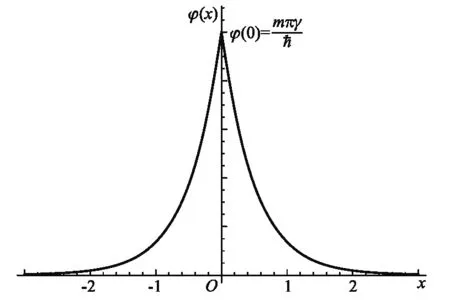
图1 单delta势约束下的波函数示意图
2 双delta势阱约束下傅里叶变换法求解
当V(x)为双delta势时,有
V(x)=-γ1δ(x+a1)-γ2δ(x-a2)
(15)

(16)

(17)
仅考虑E<0,对上式作傅里叶逆变换,结果为[9]
(18)
由于双delta势关于纵轴对称,方程(1)的解一般是具有宇称性.
(19)
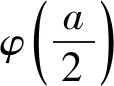

(20)
这样波函数可以最终确定出来,示意图如图2(a)所示.
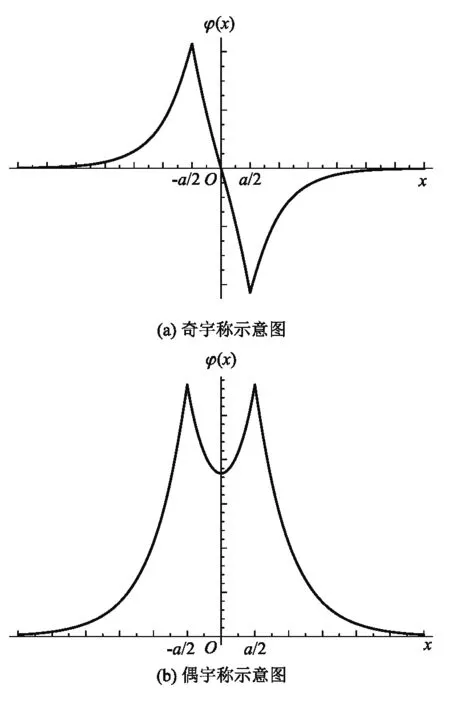
图2 双delta势约束下的波函数示意图
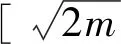
(21)
这样波函数可以最终确定出来,示意图如图2(b)所示.
3 三delta势阱约束下傅里叶变换法求解
当V(x)为三delta势时,有
V(x)=-γδ(x+a)-γδ(x)-γδ(x-a)
(22)
对相应的薛定谔方程做傅里叶变换可得
(23)
仅考虑φ(-a)eiwa+φ(0)+φ(a)e-iwa≠0且E<0,有
(24)
对上式作傅里叶逆变换,结果为[9]
(25)
利用波函数在x=-a、0、a处的取值以及归一化条件可以确定系数φ(-a)、φ(0)、φ(a)及E的取值.由式(25),也可以画出具有奇偶宇称性的波函数的示意图如图3所示.
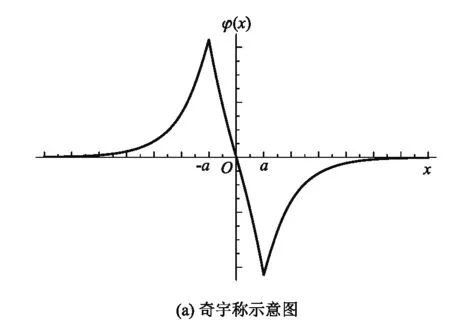
图3 三delta势约束下的波函数示意图
4 奇数(2n+1)个delta势约束下方程的求解
当V(x)为delta势时
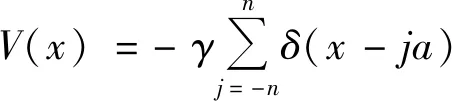
(26)
对三delta势阱约束下的薛定谔方程作傅里叶变换,得
(27)
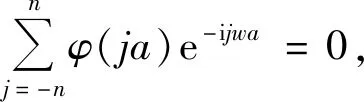
(28)
依然考虑E<0的情况,作傅里叶逆变换,结果为[9]
(29)
利用x=ja处波函数特殊性及归一化条件:
(i=-n,-n+1,…,n)
(30)
(31)
可以定出能量E和φ(ja),最终可以确定出波函数.由(式29),也可以画出具有奇偶宇称性的波函数(这里选择n=3时)的示意图如图4所示.
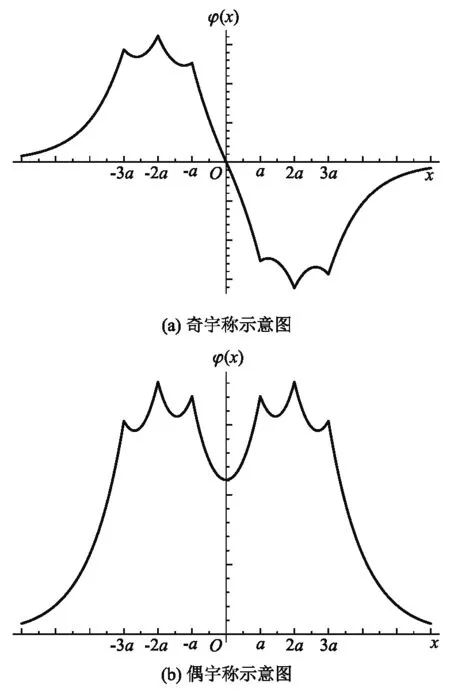
图4 7个delta势约束下的波函数示意图
5 偶数(2n)个delta势约束下方程求解
当V(x)为delta势时,有
(32)
对三delta势阱约束下的薛定谔方程作傅里叶变换,得
(33)
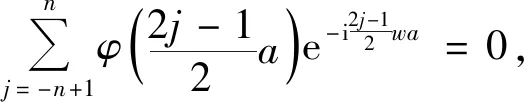
(34)
依然考虑E<0的情况,作傅里叶逆变换,结果为[9]
(35)
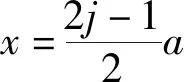
(36)
(37)
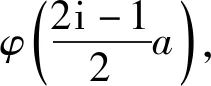

图5 8个delta势约束下的波函数示意图
5 结论
虽然基于傅里叶变换法的薛定谔方程的求解在量子力学中不多见,但这的确是一种简捷有效的方法.从本文讨论的具有若干delta势阱约束下的薛定谔方程的傅里叶变换法求解过程可以看出这一点.
