考虑多时间约束和机器效率的柔性作业车间调度问题建模及优化 *

梁晓磊 马千慧 李章洪 刘星雨 张孟镝

(武汉科技大学汽车与交通工程学院，湖北 武汉 430065)

柔性作业车间调度问题(flexible job shop scheduling problem, FJSP)是作业车间调度问题(job-shop scheduling problem, JSP)的一个重要分支，多机器选择和工序排序问题是比确定加工路径的调度问题更为复杂的NP-hard问题[1]，也是制造业中亟需解决的一类问题。针对这一问题，许多学者研究了不同条件下的柔性作业车间调度问题。如在模型构建方面，有考虑加工时间不确定性并利用时间Petri网建立模型[2]、基于设备状态-能量分布的绿色低碳调度模型[3]、考虑工件安装和定位调整时间的模型[4]、具有运输时间和以总拖期最短为目标[5]以及具有增强信息素关系的蚁群序列和运输时间的模型[6]。此外，大多数考虑时间因素的FJSP研究也都是以最小完工时间为目标[7-9]。在求解方法的研究中，主要采用智能算法，如结合仿生杂交细菌觅食优化算法和模拟退火算法求解FJSP[10]、粒子群算法和人类学习优化算法混合[11]、社会蜘蛛优化与遗传算法混合求解FJSP[12]等，这些研究表明，智能算法在求解FJSP方面具有较好的效果，成为研究的主流。可见，目前的研究主要集中在独立时间因素或以最小完工时间为目标的柔性作业车间调度，较少综合考虑多时间和多目标因素，特别是对工序间运输时间和机器效率的影响研究不足。在实际制造过程中，包括运输时间在内的多时间因素以及使机器负载均衡化是不可忽略的重要因素[13-15]。

因此，本文提出同时考虑工件运输时间、到达时刻和交货期，构建以最小化完工时间和最大化机器效率为目标的柔性作业车间调度模型，任务调度会受到工件的紧前工序、机器上的前置工序、机器可用时间段的影响。基于遗传算法，在变异操作过程中考虑机器的利用率对机器重新选择，并设计了一种分段交叉和局部种群扩张策略对模型进行求解。

1 考虑工件运输时间和机器效率的FJSP问题及模型描述

1.1 问题描述

在传统的JSP中，工件选择的机器和加工时间都是固定的，调度目标只需确定工序的加工顺序。在FJSP中，每道工序可以选择可加工机器集中的一台机器加工，且加工时间不同。与生产实际相一致，本文研究最大化机器效率下具有工序无关的运输时间和部分柔性作业特点的车间调度问题。问题描述如下：一个生产调度包含n个工件和m台机器，每个工件的操作工序不同，每道工序有不同的可选机器，在不同机器上的加工时间和运输时间也不相同，每个工件的到达时刻和交货期是确定的。调度目标是为每道工序选择最合适的机器、确定每台机器上各工件工序的最佳加工顺序，使工件的完工时间和机器效率综合最优。

1.2 模型假设

对于构建的模型，根据作业要求，做如下假设：

(1)所有机器在加工前准备就绪，所有工件严格按照到达时刻加工。

(2)在给定时间内，每个工件加工一旦开始不可中断，即加工过程为非抢占式。

(3)任意机器同一时刻只能加工一个工件，任意工件同一时刻只能被一台机器加工。

(4)不同工件间没有加工顺序约束；同一工件的工序需按照工艺顺序加工。

(5)任意工序一旦加工完成，就立即运输到下一工序加工机器，不考虑成批运输。

(6)工件交付受交货期限制，即每个工件最后一道工序的最大完工时间不大于交货期。

(7)不考虑机器故障和运输资源。

1.3 符号和变量定义

模型符号的定义如下：

Ji：表示第i个工件(i∈[1,n])。

Mk：表示第k台机器(k∈[1,m])。

Oi,j：表示第i个工件的第j道工序(j∈[1,h])。

Ut,i,j,k：表示t时刻机器Mk可加工工序数量。

Pi,j,k：表示工序Oi,j在机器Mk上的加工时间。

Ti,l,k：表示工件Ji在两个不同机器Ml和Mk之间的运输时间(l∈[1,m])。

FTk：表示机器Mk从开始加工到结束加工之间的空闲时间。

MSk,MEk：表示机器可用时间段的开始时间和结束时间。

Ei,j,k：表示工序Oi,j在机器Mk上的完工时间。

定义Oi,(j-1)表示Oi,j的紧前工序，Oi′,j′表示Oi,j当前所在机器的前置工序。则，

Ei′,j′,k：表示工序Oi′,j′所对应的完工时间。

每个工件的到达时刻和交货期是给定的：

Ri：表示工件Ji的到达时刻。

Di：表示工件Ji的交货期。

L：表示一个极大的正数。

决策变量的解释如下：

Xi,j,k：如果工序Oi,j选择机器Mk进行加工，则Xi,j,k=1，否则Xi,j,k=0。

Yv,g,i,j,k：如果工序Ov,g在机器Mk上比工序Oi,j先加工，则Yv,g,i,j,k=1，否则Yv,g,i,j,k=0(v∈[1,h],g∈[1,h])。

Z(Mk)：如果当前机器正在使用，则Z(Mk)=1，否则Z(Mk)=0。

1.4 模型建立

(1)

其中：k∈[1,m]

f2=min(maxEi,j,k)

(2)

其中：l∈[1,n],j∈[1,h]

Z(Mk)=0

(3)

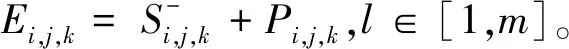
Z(Mk)=1

(4)

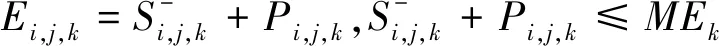
(5)

(6)

其中：v∈[1,n],g∈[1,h]

Ut,i,j,k=1

(7)

(8)

(9)

(10)

(11)

当j=h时，Ei,j,k≤Di

(12)

(13)

式(1)表示第一个目标函数，最大化机器效率；式(2)表示第二个目标函数，最小化工件最大完工时间；式(3)、(4)表示考虑了运输时间约束和机器可用时间段的工件完工时间的计算；式(5)、(6)表示每台加工机器的能力约束；式(7)表示每个工件同一时刻只能被分配给一个加工机器；式(8)表示同一工件中两个操作工序之间的优先约束；式(9)表示同一台机器上两个操作工序之间的优先约束；式(10)表示只有在当前机器可用时才能加工工件；式(11)表示运输时间约束；式(12)表示工件的交付受交货期限制；式(13)表示工件的任意一道工序的可选机器至少有一种，每一台机器上可以存在循环操作。

根据以上约束模型，考虑设备使用情况和加工机器的冲突，避免每次工件选择加工时间短的机器进行加工，造成单一机器使用频率过多，其余机器大量空闲，以致机器利用不均衡，现设置第一个目标最大化机器效率；考虑到车间效率，设置第二个目标最小化最大完工时间，目标函数构建如下：

(1)最大化机器效率

(14)

在此定义机器效率用每台机器开始加工到结束加工之间的空闲时间和计算。

(2)最小化最大完工时间

f2=min(maxEi,j,k),l∈[1,n],j∈[1,h]

(15)

2 求解柔性作业车间调度问题的改进遗传算法设计

2.1 算法编码及解码策略设计

(1)分段式编码策略

本文FJSP在传统JSP基于工序编码的基础上设计了分段编码策略，将两个子问题编码到一条染色体上，每个基因位用整数表示，该染色体由两部分组成，第一部分采用基于工序的编码，用来确定工序的加工先后顺序，工件号出现的次数就表示该工件的工序数；第二部分为基于机器分配的编码，用于选择工序的可加工机器，基因位上的数值表示工序可选机器集中从左往右的第几台机器，并不是表示实际的加工机器编号。这两部分染色体长度均为总工序数。为解释算法的编码和解码过程，本文构建了小规模部分柔性作业车间调度问题案例进行说明。表1、2是一个3×5(3个工件、5台机器)规模问题实例和运输时间表，其中“-”表示某一工序不能在该机器上加工。下文以该3×5规模问题为例说明编码过程，结合两种编码的染色体结构如图1所示。

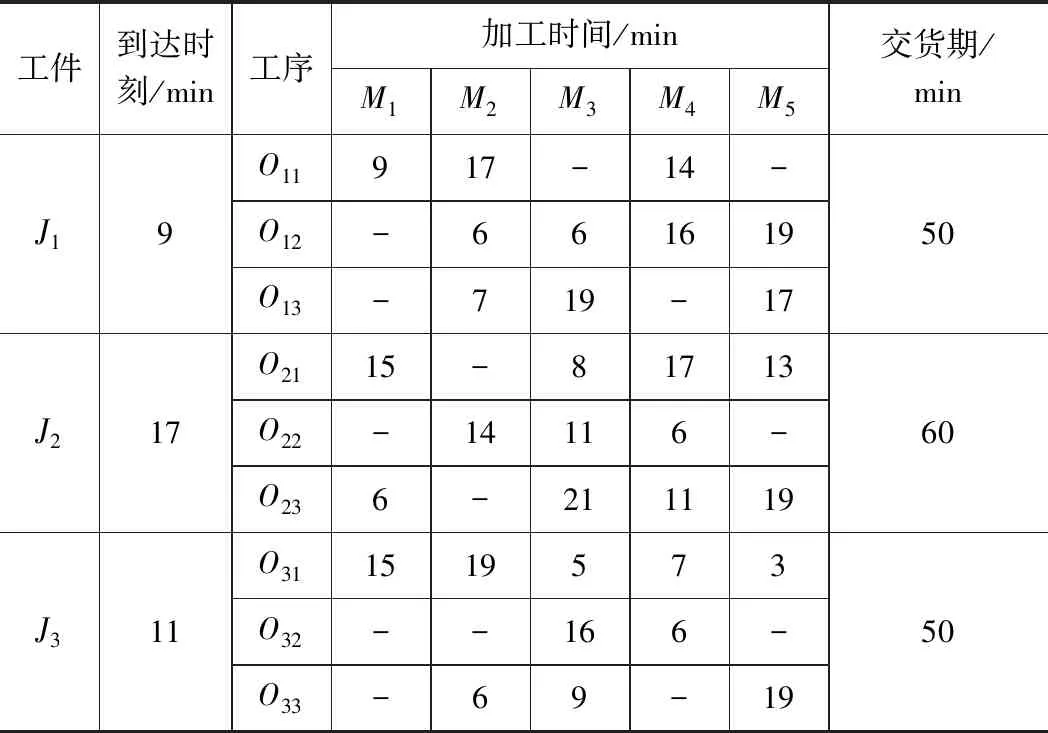
表1 3×5规模问题实例

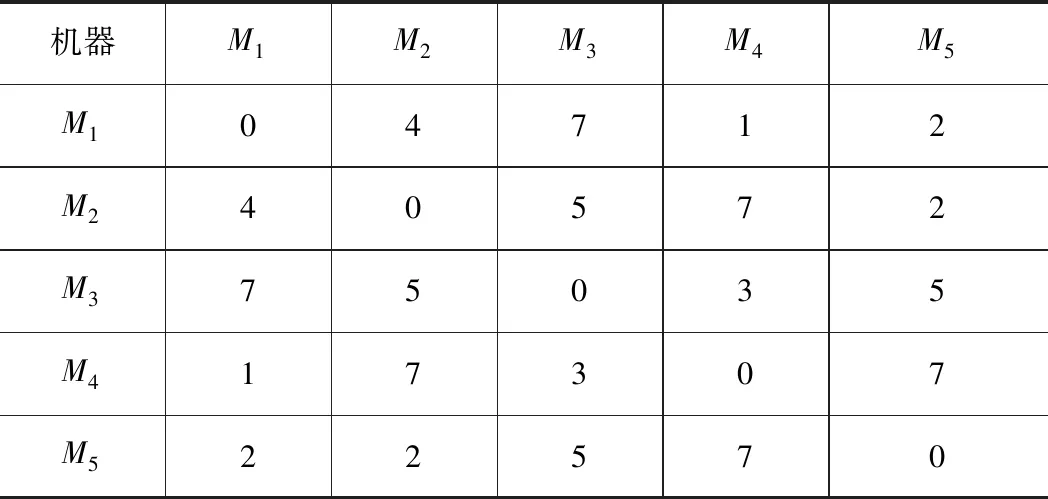
表2 实例运输时间

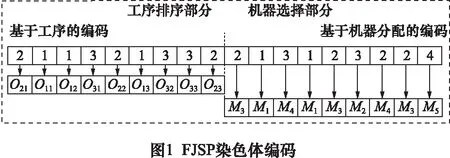
图1工序排序部分所示一个工序编码为[2 1 1 3 2 1 3 3 2]，染色体长度为9。第一个基因位上的数值2表示加工工件J2的第一道工序O21；第二个基因位上的数值1表示加工工件J1的第一道工序O11，以此类推。同样，图1机器选择部分所示一个机器编码为[2 1 3 1 2 3 2 2 4]，染色体长度亦为9。第一个基因位上的数值2表示工序O21选择第二台可以选择的机器M3，第二个基因位上的数值1表示工序O11选择第一台可以选择的机器M1，以此类推。

(2)插入式解码策略

①机器选择解码

对于机器选择部分，从左到右依次解码机器染色体，转换成机器矩阵JM和时间矩阵T。以表1、2实例为例，如图1所示的一个染色体编码，机器选择部分[2 1 3 1 2 3 2 2 4]转换成机器矩阵JM=[3 1 4 1 3 2 4 3 5]和时间矩阵T=[8 9 16 15 11 7 6 9 19]，其中JM中的基因位表示工序，基因位上的数值表示机器编号，如第一个基因位上的数值3表示工序O21选择机器M3，同样地，T中的基因位表示工序，基因位上的数值表示该工序在相应机器上的加工时间，如第一个基因位上的数值8表示工序O21在机器M3上的加工时间为8。

②工序排序解码

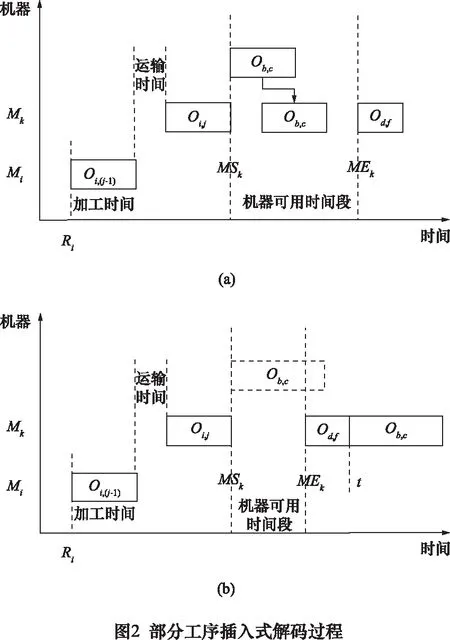
对于工序排序部分，从左到右依次解码工序染色体，得到最佳加工工艺顺序，再通过JM和T得到每一道工序的相应加工机器Mk、加工时间Pi,j,k和运输时间Ti,l,k；根据式(3)、(4)计算工件的最早开始加工时间和完工时间。如果该工序是机器上的第一个操作，只需考虑其紧前工序的完工时间；如果该工序是工件的第一道工序，则需要比较该工件的到达时刻和加工机器前置工序的完工时间的大小；否则，需要考虑机器的可用时间段是否满足工件的插入，当某一工件满足式(10)时，部分工序插入式解码过程如图2a所示，不满足时如图2b所示。

2.2 遗传操作策略改进

(1)混合初始化设计

初始解的质量影响算法的收敛速度和搜索性能。当前此类问题通常采用随机初始化的方法，但这种方法没有考虑时间约束，降低了生成初始可行解的效率。为了充分考虑多时间因素，在初始化阶段加入加工时间和运输时间约束，设计了一种混合策略初始化种群，工序排序部分采用随机初始化，机器选择部分采用混合初始化，即对80%染色体的工序选择加工时间和运输时间最短的机器，20%染色体的工序在其可选机器集中随机选择一台机器加工，使种群在保持多样性的前提下尽量选择优化结果好的个体。根据3×5规模问题实例，得到采用随机初始化和混合初始化两种方法下的初始解对比图如图3所示，从图中可以明显看出改进后的初始解更优。

(2)适应度值计算

本文模型以机器效率最高和完工时间最短为目标，为简化计算，在此采用加权方式对两个目标综合，构建适应度函数。适应度值计算如下：

F=ω1f1+ω2f2

(16)

式中：ω1、ω2取值在[0,1]且ω1+ω2=1。根据实际决策偏好(时间和效率)可调整ω1、ω2的大小，以满足不同决策者对两个子目标的要求。基于上述方式进行染色体适应度计算，作为遗传选择操作基础。

轮盘赌是遗传算法中一种常用的随机选择方法，这种比例选择操作能够使种群快速地逼近最优解。本文选择操作采用最优个体保存和轮盘赌结合的选择策略，最优个体保存是将种群中的最优个体直接复制到下一代，然后采用轮盘赌依据个体的适应度值计算每个个体在后代中出现的概率，以随机选择个体构成子代种群。

(3)交叉变异操作设计

①交叉操作设计

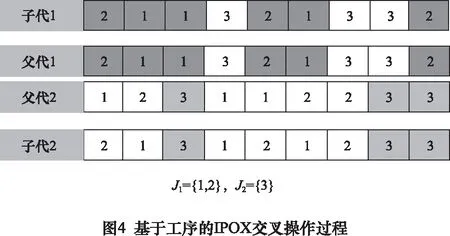
固定的交叉概率会使得个体在产生新子代的过程中缺乏适应性，无法根据种群需求进行调整。本文基于S-自适应交叉概率[16]设计了个体分段交叉策略，工序排序部分采用IPOX交叉方式，将所有工件随机分成两组，仅交叉父代染色体中工件的工序序列，直接复制工件中工序选择的机器到子代，而机器选择部分采用随机交叉方式。以3×5规模问题为例的交叉操作过程如下图4所示，复制父代1中包含在J1同一位置的工序到子代1，复制父代2中包含在J2同一位置的工序到子代2；父代1中包含在J1中的工序按顺序复制到子代2剩余位置，父代2中包含在J2中的工序按顺序复制到子代1剩余位置。

②变异操作设计

为了保持种群多样性，变异操作采用分段变异方式。对于工序排序部分，实施基于工序变异的单点变异操作；对于机器选择部分，基于机器利用率的机器选择策略在原有变异策略的基础上，计算每个父代个体每台机器的使用频次，在工序顺序不变的前提下，以一定概率对机器进行轮盘赌选择，重新选择时，以机器的使用频次为依据，使用频次越小，被选择的概率越大。以3×5实例问题为例，某一个体[1 1 2 3 2 1 3 3 2 2 1 3 1 2 3 1 3 1]机器选择部分对应的实际机器号为[2 2 4 1 3 5 3 5 1]，其中机器1被选择2次，机器2被选择2次，机器3被选择2次，机器4被选择1次，机器5被选择2次，机器4使用频次最小，使用轮盘赌操作使其被选择的概率最大，从而缩短机器的最大完工时间，实现机器效率最大化。

(4)局部种群扩张策略

针对传统的遗传算法采用交叉变异后的个体扩充种群，可能造成部分解信息丢失。在此常规种群构建基础上，本文采用一种局部种群扩张策略，从父代和子代混合个体中进行选择，这样父代个体和交叉变异得到的个体具有同等的选择机会，既能将最优个体保留到下一代，又便于保持子代的多样性。

2.3 算法流程

基于改进遗传算法求解考虑运输时间的柔性作业车间调度问题的步骤如下：

步骤1设置参数。确定种群大小P、最大遗传代数M、选择概率Pa、变异概率Pm；

步骤2 种群初始化。考虑调度问题的时间因素，基于分段式编码和插入式解码以及混合策略进行种群初始化；

步骤3 采用最优个体保存和轮盘赌结合的复合选择策略进行选择，选出交叉个体；

步骤4 采用S-自适应交叉概率对种群个体分段交叉；

步骤5 对工序排序部分进行单点变异，机器选择部分按照一定概率选择加工时间和运输时间短的机器；

步骤6 保持工序顺序不变，机器选择部分根据一定概率基于机器利用率进行轮盘赌选择；

步骤7 更新目标适应度值比较大小，若满足输出条件结束运行，否则，采用局部种群扩张策略重新插入新种群，执行步骤3。

3 案例求解与结果分析

3.1 案例及算法参数设置

为了验证模型和算法的有效性，以10×8算例[17]和12×10算例[5]数据进行测试，两个算例运输时间参考文献5中数据。

为了进一步比较算法的性能，采用传统遗传算法(genetic algorithm，GA)、粒子群算法(particle swarm optimization，PSO)、模拟退火算法(simulated annealing，SA)和本文改进遗传算法(improved GA，IGA)分别进行测试。采用Matlab R2018b对算法进行编程实现并对实例问题进行求解验证，实验在平台(Intel(R) Core(TM) i5-6500 CPU @ 3.20GHz 3.19 GHz，内存8.00 GB)上进行。算法参数设置如下：种群规模和迭代次数统一设置为P=200、M=200；其中PSO参数设置参考文献18，学习因子c1、c2取值2.05，惯性权重ωmax=0.9，ωmin=0.4；SA参数设置参考文献[19]，退火起始Tb=1 000，终止温度Te=0.001，降温速度r=0.98，迭代步长L=200；本文算法IGA设置选择概率Pa=0.8，变异概率Pm=0.1；为方便做对比，GA中设置和IGA相同的参数。设置算法IGA、GA、PSO达到设定迭代次数就终止算法，算法SA达到设定终止温度Te就终止算法。

表3 12×10规模问题实例

表4 实例运输时间

3.2 案例求解

以12 × 10 规模问题为例 。 求解中假设取时间和机器效率的目标权重分别为 0.8 和 0.2 ，得到考虑运输时间的最优调度甘特图如图 5 所示。基于优化结果(图 5 可知， 求解获得的最好适应度值调度解的工序编码为 [201 901 1001 301 401 701 501 902 601 702 1002 402 101 202 801 602 1101 903 1201 802 302 502 603 203 1202 102 904 303 403 1003 905 803 1102 103 1004 1203 304 906 804 ]，机器编码为 [4 7 9 3 8 4 5 7 9 8 6 4 7 9 3 10 5 4 7 3 8 6 10 4 7 1 2 8 6 4 2 1 0 7 4 10 1 2 4 10 ]。 解释如下:其中，201 在纵坐标对应值为4，表示第2个工件的第一道工序在机器4 上加工， 距离坐标原点的这段时间对应于工件2的到达时刻8,因此201的最早开始加工时间为8，再经过10个单位的加 工时间，它的完工时间为18；工件2的第2道工序 202 在机器9上加工，机器4到机器9的运输时间为5，此时机器9上有前置工序1001和601，工序1001的最早开始加工时间为到达时刻15，再经过7个单位的加工时间，其完工时间为22，工序601的到达时刻为19 ,其最早开始加工时间为 max (19,22 )=22,再经过 11 个单位的加工时间，其完工时间为33，因此工序202的最早开始加工时间为 max( 33 ,18+5 )=33。同理，10 × 8 规模问题类似。

图6 为不采用基于机器利用率的变异策略的调度甘特图，和图 5 相比较，将机器利用率作为影响因素考虑进调度方案可以明显缩短工件的完工时间，并且有效降低各机器的空闲时间，增大机器使用率，从而提高机器效率。

3.3 算法性能测试

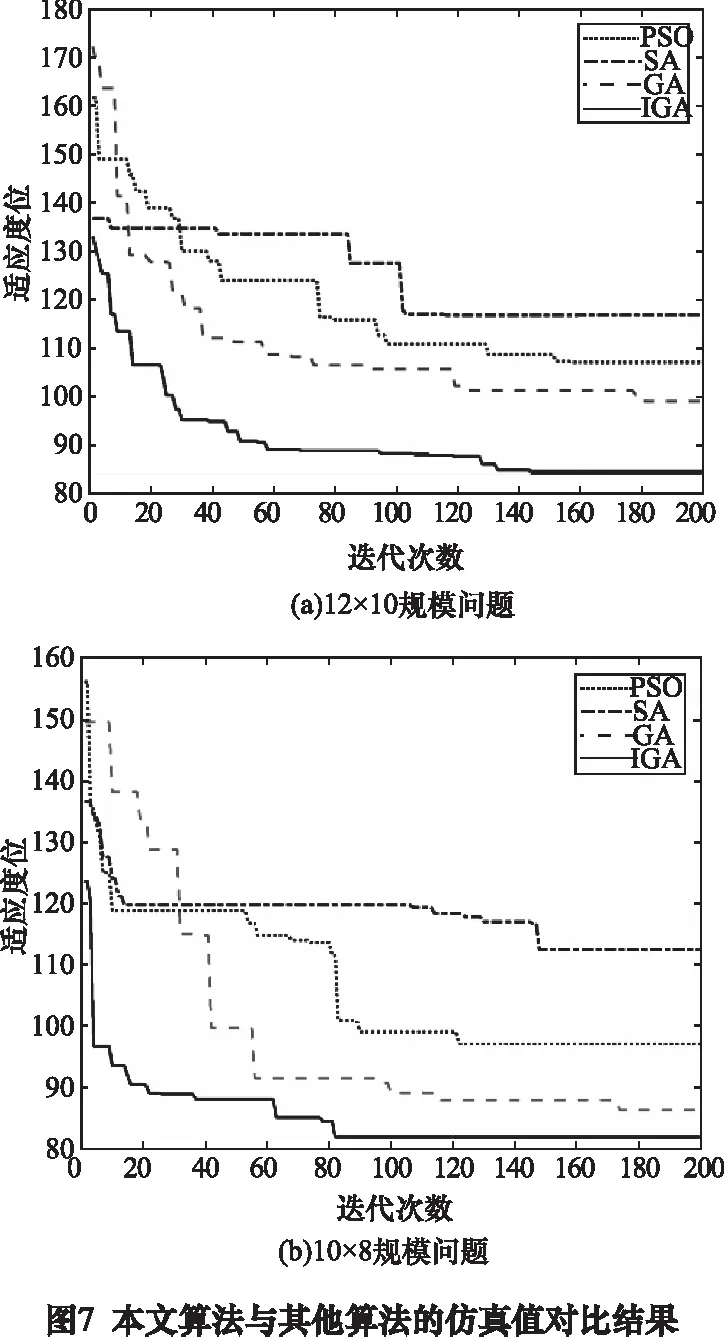
为测试算法性能，用上述两组问题实例对GA、PSO、SA和本文算法IGA分别进行测试，优化目标为最小化最大完工时间和最大化机器效率。运算取时间和机器效率的目标权重分别为0.8和0.2，针对每个不同的实例分别连续运行20次，并分别记录其最优值和平均值，测试结果见表5。基于运行时间和最优解，本文提出的IGA 算法明显优于PSO、SA 算法，虽然与GA相比，运行时间更长，但是获得的最优解比GA 更好，可以证明改进的遗传算法在解决实例问题中能找到更好的结果，具有更好的优化能力。

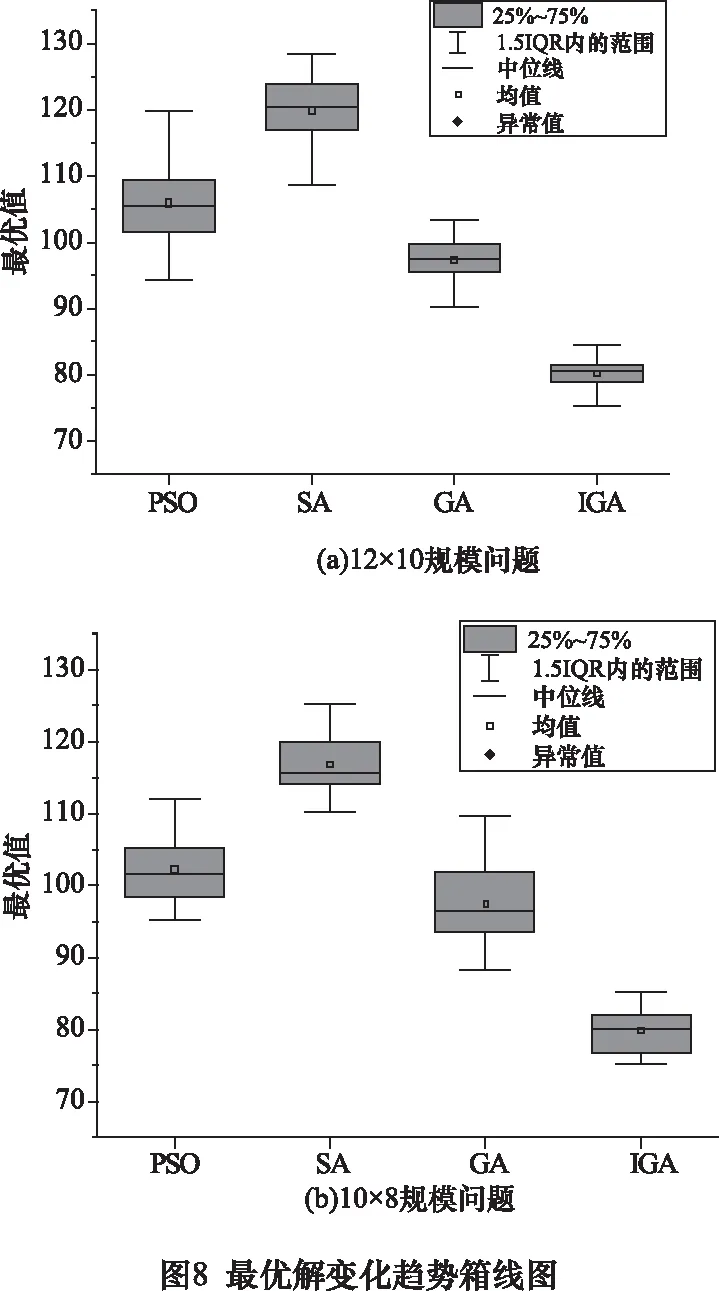
上述4种算法求解两组问题实例的最优解对比和最优解变化趋势箱线图如图7和图8所示，从图7中可以看出，在求解柔性作业车间调度问题实例时，与其他3种算法相比，本文提出的改进遗传算法明显降低了适应度值，克服了遗传算法的早熟收敛，并加快了遗传算法的收敛速度；从图8中可以看出，绝大多数最优解集中在中位值和平均值下方，证明本文改进算法有一定的优越性且提高了解的稳定性。

表5 不同算法测试结果对比

3.4 权重系数分析

ω为目标函数的权重系数，权重的分配可根据决策者的要求进行设置。在更加关注设备使用的情况下，即机器效率，则设计ω1>ω2；在更多关注车间效率的情况下，即最大完工时间，则设计ω1<ω2；当两者同等考虑时，则设计ω1=ω2。

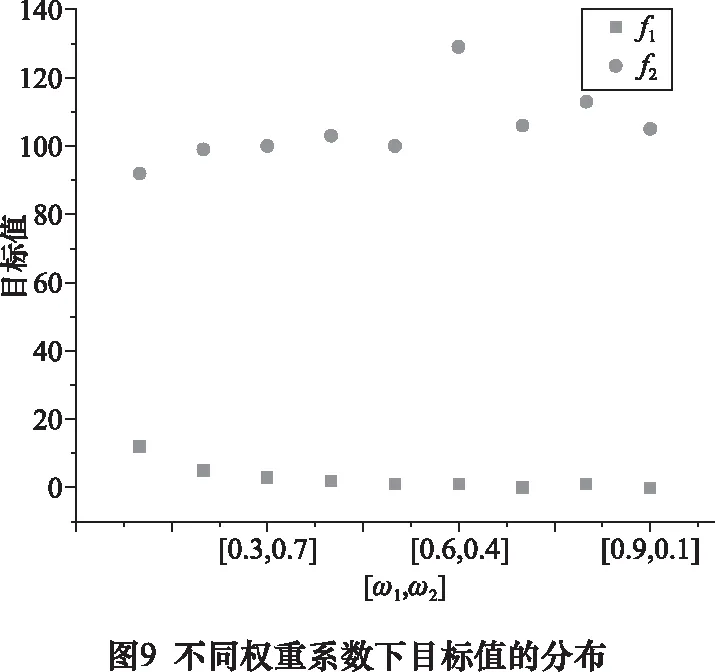
以12×10案例为例，设置不同权重系数取值，用本文改进遗传算法求解模型中机器效率和完工时间目标，实验结果如表6所示，同时给出不同权重系数下目标值的分布情况如图9所示。可以看出，调度过程中降低机器效率的同时会相应增大完工时间，说明目标权重取值大小会影响车间调度效率，决策者可以通过对目标的重视程度调整ω取值从而获得最优调度结果。

4 结语

本文在传统FJSP模型上，综合考虑了加工时间和运输时间等影响因素，增加了工件的到达时刻、交货期约束及机器利用率约束，建立了以最大化机器效率和最小化完工时间为目标的FJSP模型。针对该模型，设计了一种改进遗传算法对其进行求解。算法中采用了混合初始化、复合选择和局部种群扩张等策略，提升遗传算法求解此类FJSP问题能力，避免陷入局部最优。实例测试结果也验证了模型和算法的有效性。在下一步研究工作中，将重点研究考虑加工和运输中随机因素对柔性车间调度问题目标的影响及应用多目标优化方法的求解设计。