多组合设备的时间延迟优化研究 *

潘春荣 龙志强

(江西理工大学机电工程学院，江西 赣州 341000)

时间延迟过长会对晶圆质量造成损失。Wang J、Yang F J等[1-2]将驻留时间延迟作为约束，建立了生产系统的Petri网模型，对单臂组合设备进行稳态调度优化。潘春荣等[3]将时间延迟优化作为目标，提出了一种等待时间分配策略，对单臂组合设备进行调度。在此基础上，Xiong W Q等[4]开发了3种启发式算法对机械手等待时间进行进一步分配，从而有效降低了单臂组合设备的时间延迟。

上述学者对单台组合设备进行了调度，对于多组合设备，由于各组合设备间耦合依赖性强，多组合设备的调度更加复杂。Hu J等[5]考虑机械手、加工模块(process module, PM)约束，构建了相应数学模型，并提出基于分解的启发式算法对模型进行求解。Sakai M等[6]构建了高效的多组合设备Petri网模型，基于此，Bai L等[7]通过配置不同BM的容量，达到了系统的调度周期下限。对于多组合设备的时间延迟约束问题，Bao T等[8]从混合整数规划的角度，提出了生产系统的周期调度策略。Yan Y等[9]考虑时间延迟约束，提出了同时适用于单臂、双臂多组合设备的非周期调度模型，并改进了一种动态规划算法对模型进行求解。

上述研究大多对时间延迟进行分析，仅有少量文献将时间延迟作为目标进行优化，特别地，在多组合设备中，时间延迟的优化更是鲜有涉及。为平衡各工序的作业负载，组合设备常引入并行加工模块。本文对具有并行加工模块的单臂线形多组合设备进行研究，将时间优化问题转化为以降低时间延迟为目标的机械手等待时间分配模型，并提出一种改进多目标灰狼算法对问题进行求解。

1 稳态生产过程描述

由k(k≥ 2)台组合设备通过BM连接而成的设备称为k-组合设备，设Nk= {1, 2,…,k}，符号Ci(i∈Nk)表示第i台单组合设备。将LL(Load Lock, LL)视为工序0，连接设备Ci与Ci+1(i∈Nk-1)的BM视为设备Ci的b[i]工序或设备Ci+1的工序0，晶圆在设备Ci(i∈Nk)的最后工序为n[i]，则Ci共有n[i]+1道工序。令Ωk= Nk∪{0}，设PSij(i∈Nk,j∈Ωn[i])表示设备Ci的工序j，工序PSij中包含mij个并行PM，则晶圆在k-组合设备中的生产过程可以描述为：PS10→PS11→PS12→… →PS1(b[1])→PS21→… →PS(k-1)(b[k-1])→PSk1→… →PSk(n[k])→PSk0→PS(k-1)(b[k-1]+1)→… →PS(k-1)0→PS(k-2)(b[k-2]+1)→… →PS20→PS1(b[1]+1)→… →PS1(n[1])→PS10。

稳态下工序PSij的生产过程包括晶圆载入PM、晶圆在PM中加工、机械手卸载晶圆前等待、机械手卸载晶圆、机械手移动等活动，各活动的符号表示及耗费时间如表1所示。

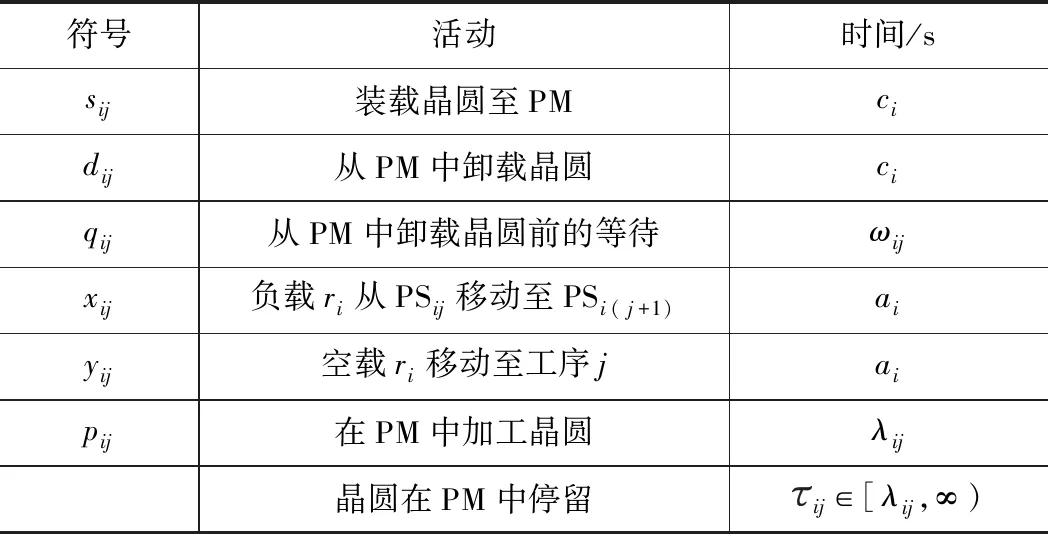
表1 设备Ci中各活动时间

2 调度分析

2.1 单组合设备调度分析

对于工序PSij(i∈Nk,j∈Nn[i]-1)，稳态单位周期内，机械手活动序列为：dij→xij→si(j+1)→yi(j-1)→qi(j-1)→di(j-1)→xi(j-1)→sij。在PSij(i∈Nk,j∈Nn[i]-1)的机械手活动序列基础上，将si(j+1)更换为si0，即可获得PSi(n[i])的机械手活动序列。对于工序PSi0，机械手活动序列为：di0→xi0→si1→yi(n[i])→qi(n[i])→di(n[i])→xi(n[i])→si0。工序PSij包含mij个并行PM，稳态下mij片晶圆同时进行加工，则工序PSij的生产周期πij为：

(2)

将生产周期中的时间延迟及机械手等待时间去除，可获得工序PSij的作业负荷θij：

(3)

(4)

由机械手活动序列可获得机械手的活动周期ψi为：

(i∈Nk)

(5)

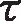
(i∈Nk,j∈Nn[i])

(6)

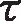
(i∈Nk)

(7)

令设备Ci(i∈Nk)的生产周期为πi，由文献[3]可知，稳态下对设备Ci进行周期调度，需满足各工序加工时间均与机械手活动周期相等的条件，即πi=πi0=πi1=…=πi(n[i])=ψi。为达成该条件，可调节机械手等待时间，使得各工序生产周期相等。

2.2 k-组合设备调度分析

设k-组合设备的系统生产周期为π，Πi为设备Ci(i∈Nk)的基本生产周期，用于衡量各设备的作业负荷，其中Πi=max{θi0,θi1,…,θin[i],ψi1}，当Πp=max{Πi|i∈Nk}时，称设备Cp为瓶颈设备。通过调整机械手等待时间，使得π=Πp，系统达到最优生产周期，此时工序PSij的时间延迟ρij计算如下：

ρij=ij-λij=mij·Πp-(λij+4ci+3ai+ωi(j-1)),

(i∈Nk,j∈Nn[i])

(8)

ρi0=i0-λi0=mi0·Πp-(4ci+3ai+ωi(n[i])),

(i∈Nk)

(9)

结合式(1)～(2)、(8)～(9)可知，在某系统周期下，增大机械手等待时间，能有效地降低时间延迟。特别地，由于晶圆在工序0与BM中不进行加工，将时间延迟更多的分配在工序0与BM中，能够显著降低工序PSij(j∈Nn[i])的有效时间延迟。因此，时间延迟优化问题可以表示为：

(10)

min(f2)=min(max{ρij|i∈Nk,j∈Nn[i]}),

j≠b[i]

(11)

(12)

(13)

ωi(j-1)≤mij·Πp-(λij+4ci+3ai)，

(i∈Nk,j∈Ωn[i])

(14)

(15)

式(10)～(12)为时间延迟优化的3个子目标，式(10)表示PM中时间延迟总和最小，式(11)表示最小化PM中的最大时间延迟，式(12)表示LL与BM中时间延迟最大，由此，具有并行加工模块的多组合设备时间延迟优化问题的调度目标为min(F) =min(f1,f2,f3)。式(13)保证了组合设备最优周期调度的条件，式(14)、(15)分别为时间延迟、机械手等待时间的非负约束。

3 调度算法

本文模型为多目标优化模型，采用启发式算法更易于寻找全局最优解。灰狼优化算法(grey wolf optimizer, GWO)[10]参数少、对参数依赖性弱、易实现，并且能够在全局搜索与局部寻优间实现平衡，在问题求解精度与收敛速度方面均有良好性能[11]。因此，采用GWO算法对模型进行求解。鉴于本文模型为多目标优化模型，故引入MOEA/D算法[12]并对其进行改进。

3.1 MOEA/D-GWO算法改进

(1)目标分解

采用切比雪夫聚合方法将多目标优化转化为多个单目标优化问题：设各目标的理想点为zi*(i∈{1, 2, 3})，在可行解空间Γ中均匀分布一组权重向量εi，如式(16)所示，其中pop为种群数量，并由切比雪夫策略将min(F) =min (f1,f2,f3)分解成3个单目标优化问题的最优解，如式(17)所示。

(16)

minF(x|εi,z*)=mingte(x|εi,zi*)=

(2)种群迭代更新

根据欧几里得距离最短，将εi进行聚类分析，形成邻域；随机选取两个邻域的εi，对解集合进行GWO算法迭代更新。

(3)灰狼变异

为增加种群多样性，避免局部最优，对非“精英”狼进行高斯变异，若变异产生的新解优于原解，则采用新解，变异方式如下：

(18)

σ=σmax-t·(σmax-σmin)/Gmax(19)

式(18)中xmaxv、xminv为第v维决策空间的上下界，Xnew为经过变异后产生的灰狼新位置，U[1,2,3]表示1到3之间均匀分布的随机整数，Gaussian(0,σ2)为服从均值为0，方差为σ2的高斯分布的随机数，σ2从σmax到σmin线性减少，计算方式如式(19)所示。

(4)修复不可行解

对不可行解进行修复，修复方式如式(20)，其中rand为(0, 1)均匀分布的随机数，Xnew为修复后灰狼的位置。

Xnew=rand·(xmaxv-xminv)+xminv

(20)

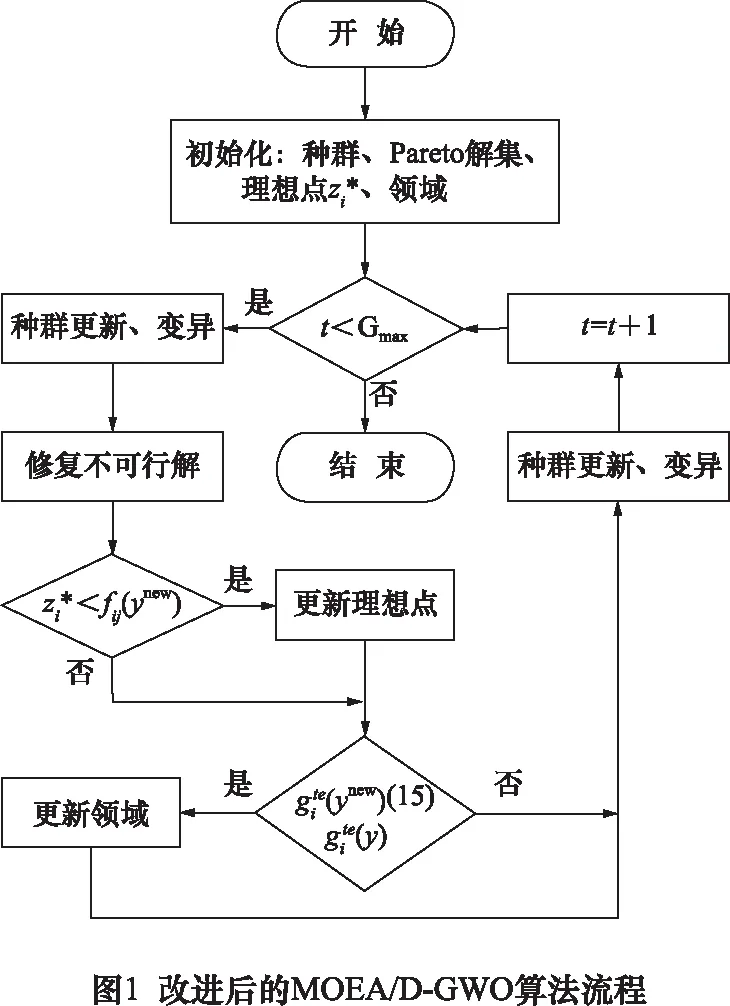
3.2 改进后MOEA/D-GWO算法流程

基于上述MOEA/D-GWO算法的改进操作，改进后算法的流程如图1所示。

4 应用实例

有一单臂线形3-组合设备对晶圆进行加工，设备C1包含2个LL，3个PM，1个BM；设备C2包含4个PM，2个BM；设备C3包含5个PM，1个BM。晶圆从设备C1的LL出发，经过各PM、BM，最终加工完成返回LL。设定各PM加工时间、机械手移动、晶圆装载与卸载时间见表2、表3。

表2 各PM加工时间

表3 机械手移动及装卸时间

该3-组合设备各工序可以表示为PS10、PS11、PS12、PS1(b[1])、PS20、PS21、PS22、PS2(b[2])、PS23、PS24、PS30、PS31、PS32、PS33、PS34，其中PS11表示PM11、PM12两个并行PM，PS32表示PM32、PM33两个并行PM。经计算，该3-组合设备为加工临界，且π=98 s。

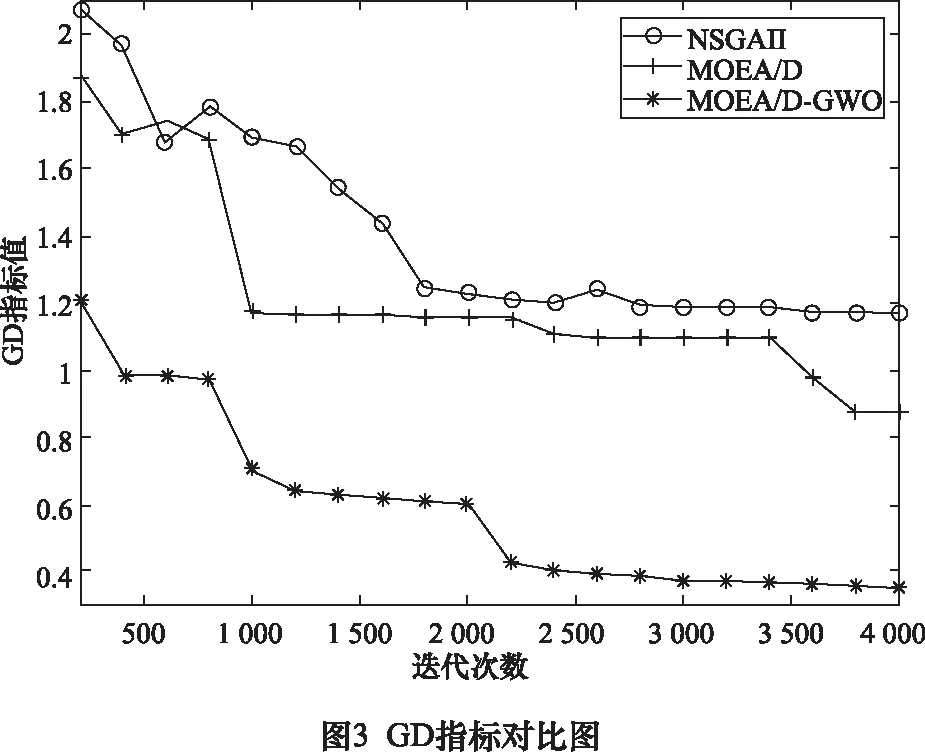
采用改进的MOEA/D-GWO算法对该案例进行求解，参数设置如下：种群数量pop=100，邻域大小为6，更新因子dmax=2、dmin=0，迭代4 000次，得到帕累托前沿(pareto front, PF)如图2所示。为评估算法收敛性，继续采用MOEA/D、NAGAII算法[13]对案例进行求解，并引入GD(generational distance, GD)指标[14]对算法性能进行评价。GD指标对比如图3所示，随着迭代次数的增加，MOEA/D-GWO算法、MOEA/D算法以及NSGAII算法均能较好的逼近PF，但MOEA/D-GWO算法的GD值更小，求解质量更优。

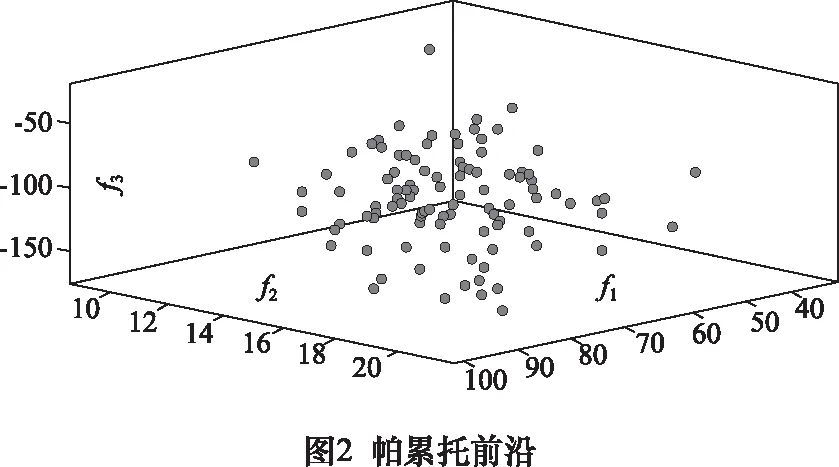
为获得最终解，设置各目标权重为(0.2, 0.4, 0.4)，对PF进行计算排序，得到最终解为ω= (ω10,ω11,ω12,ω1(b[1]),ω20,ω21,ω22,ω2(b[2]),ω23,ω24,ω30,ω31,ω32,ω33,ω34) = (17.50, 0.00, 0.25, 0.25, 2.05, 8.05, 0.13, 0.60, 3.04, 0.13, 4.88, 4.99, 3.40, 4.57, 0.16)，F= -108.87，各工序时间延迟为ρ= (ρ10,ρ11,ρ12,ρ1(b[1]),ρ20,ρ21,ρ22,ρ2(b[2]),ρ23,ρ24,ρ30,ρ31,ρ32,ρ33,ρ34) = (59.75, 0.50, 0.00, 59.75, 71.87, 13.95, 13.95, 71.87, 11.40, 13.96, 68.84, 11.12, 12.01, 5.60, 9.43)，晶圆在LL、BM中不会对晶圆质量造成损伤，有效时间延迟为在PM中停留时间，则总有效时间延迟为91.92 s。 若采用传统拉式策略，机械手等待时间ω'= (0, 0, 0, 18, 0, 0, 0, 0, 0, 14, 0, 0, 0, 0, 18)，各工序时间延迟为ρ' = (42, 18, 0, 60, 58, 16, 22, 72, 12, 17, 51, 16, 17, 9, 14)，总有效时间延迟为141 s，改进后时间延迟缩短了34.81%，改进有效。

5 结语

本文对带有并行加工模块的单臂线形多组合设备进行研究，探究了机械手等待时间对时间延迟的影响机制，以机械手等待时间为变量，建立了时间延迟的多目标优化模型，提出改进的多目标启发式算法对模型求解，并用案例验证了模型与算法的有效性。主要贡献为：

(1)构建了单臂线形多组合设备的时间延迟优化模型，为多组合设备时间延迟优化问题提供了一个解决思路。

(2)以多组合设备加工晶圆为案例进行应用，对模型及算法的有效性进行了验证，同时为具有并行加工模块的单臂线形多组合设备提供了高效可行的时间延迟优化方案。

多组合设备的时间延迟优化是个复杂的问题，本文将晶圆加工时间视为固定值，但在实际加工过程中，晶圆加工时间并非是固定不变的，而是在中心值上下波动。因此，下一步将考虑时间波动因素，对多组合设备的时间延迟优化进行更深入的研究。