FRP抗剪加固钢筋混凝土梁计算公式修正

吴林铭 王驰 李源 惠启祥 李付俊

长安大学公路学院，西安710064

纤维材料的差异、粘贴形式、锚固方式、受荷的剪跨比、混凝土强度、混凝土梁的配箍率以及混凝土梁的预损程度等，对纤维布材料性能的发挥都有不同程度的影响［1］。混凝土斜截面抗剪性能受力机理比较复杂，影响承载力的因素多，没有统一的计算公式。各国规范基于大量试验建立的半经验半理论公式进行控制设计，不同规范计算结果相差大，且这些公式对于不同尺寸FRP抗剪加固的适用情况不明确。

一些学者提出试验梁的尺寸对试验结果的影响也不能忽视，因此，Chaallal等［2］对足尺的T梁进行了试验，分析了FRP对大尺寸构件的加固效果。周英武等［3］对不同的FRP加固抗剪公式精度进行了对比分析，并指出混凝土强度是影响FRP抗剪性能的重要因素。周畅等［4］开发了一套CFRP（Carbon Fiber⁃reinforced Polymer）布预应力张拉与锚固装置，并对预应力CFRP布抗剪加固梁进行了试验研究。张智梅等［5］基于171根FRP试验梁，在前人研究的基础上提出了修正后的FRP筋抗剪承载能力计算公式。付一小等［6］设计了4组CFRP布T梁抗剪加固试验，考虑了二次受力的影响，研究加固梁在外荷载作用下的正常使用性能指标。

大部分学者仅对FRP布材抗剪加固进行了研究，而较少涉及FRP板材的试验研究。与FRP布相比，FRP板具有整体性好、强度大的特点，一条FRP板在一定程度上相当于4～8层FRP布的加固效果，不存在叠层削弱的情况。

本文基于42片FRP片材抗剪加固试验梁，在JTG/T J22—2008《公路桥梁加固设计规范》（简称规范）建议公式的基础上，考虑纤维板的材料特性及混凝土抗拉强度的影响，对规范中抗剪强度提高值进行修正，并对比公式修正前后的计算精度。

1 规范中斜截面加固承载能力计算公式

1.1 FRP梁斜截面加固承载能力计算公式

采用FRP对钢筋混凝土梁进行抗剪加固后，承载力计算的基本原理在国际上已趋于一致，即加固后的承载力为原梁承载力与纤维复合材料对承载力的贡献叠加。但在FRP对承载能力的贡献计算上存在差异，主要表现在破坏模式及FRP应力发挥的程度。JTG/T J22—2008公式分别按照美国ACI440建议公式、欧洲混凝土协会设计规范（EC2 1992）建议公式、英国混凝土协会规范建议公式（BS8110）、加拿大规范（ISIS）建议公式、中国工程建设标准化协会标准（CECS146：2003）建 议 公 式、香 港 理 工 大 学Chen&Teng建议公式和Triantafillou建议公式、Khalifa建议公式进行了对比分析。结果表明香港理工大学Chen&Teng建议公式和Triantafillou建议公式的计算公式精读较高，而加拿大、美国及欧洲规范建议公式均偏于保守。经模型试验研究，JTG/T J22—2008规范编写组考虑了片材条带间的应力分布不均匀现象，并认为加固后斜截面在破坏阶段片材已经出现滑移，即混凝土与片材之间出现不协调变形。根据规范中7.6.7条规定，采用FRP对梁、板构件进行斜截面加固时（图1），粘贴FRP后结构抗剪承载力的提高值为Vf，计算式见式（1）和式（2）。

图1 粘贴FRP抗剪加固计算图示

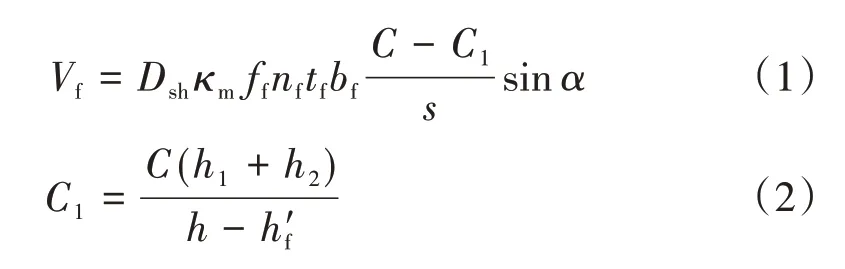
式中：Dsh为纤维应力分布系数，Dsh=1-[Le/(h-h′fh1)]sinα；h为梁的截面高度；h′f为梁顶面至上侧锚固区上边缘的距离；h1为纤维上侧锚固区压条宽度；α为纤维受力方向与梁轴线的夹角（≤90°）；Le为有效粘贴长度，；Ef为纤维复合材料的弹性模量；nf为纤维复合材料的层数；tf为每层纤维复合材料的厚度；fck为混凝土轴心抗压强度标准值；C为斜裂缝水平投影长度，C=0.6mh0，m为原构件的剪跨比，h0为梁截面的有效高度；ff为复合纤维材料的抗拉强度设计值；bf为纤维条带宽度；s为斜截面加固纤维条带间距；h2为纤维上侧锚固区压条宽度，对于U形粘贴取0；κm为纤维复合材料强度折减因子，取κm1与κm2中的较小值，κm1按下式计算，κm2可查规范。

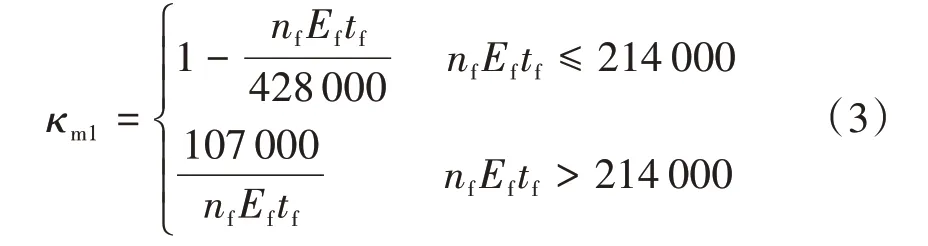
1.2 抗剪承载力计算公式的理论值与试验值对比

为直观分析规范公式的计算精度，基于42根试验梁对公式进行检验，计算抗剪承载力试验值与理论值的相对偏差，见表1。可知，有几片梁的相对偏差值非常大：①1#—4#、16#—19#、39#的试验梁均采用了较厚的碳纤维板，则理论值过小，39#试验梁的计算值甚至为负；②9#、36#、38#试验梁均采用封闭式包裹或附加锚固措施进行加固，理论值与试验值相差较大。③16#—19#试验梁截面尺寸太小，理论值过小。产生上述现象的原因是：①采用粘贴多层碳纤维布时加固效果削弱，采用碳纤维板时不存在叠层削弱的情况。因此，不能按公式的强度折减因子进行计算，须对折减因子进行修正。②公式只考虑了上下压条的锚固作用，并未考虑其他附加锚固措施（如全包裹、机械锚固等）对抗剪承载力提高值的影响。因此，当试验梁采用更加可靠的锚固措施时，试验值与理论值偏差较大。③当梁的截面尺寸过小时，有效粘贴长度相对于梁的截面高度小，导致纤维应力分布系数偏小（甚至有一片梁的承载力计算值为负值），试验值与理论值偏差较大。

表1 试验梁设计参数汇总及抗剪承载力

续表1

综上，当梁体采用较厚的碳纤维板、封闭式包裹或附加锚固措施，或梁体尺寸过小时，规范计算公式已不再适用。因此，本文通过对公式进行修正，提高公式的适用性和精确度。

2 混凝土抗拉强度对抗剪性能影响的灰色关联分析

利用灰色关联分析对混凝土抗拉强度对抗剪性能影响程度进行评价。灰色关联分析法（Grey Relational Analysis，GRA）的基本思想是根据序列曲线几何形状的相似程度来判断其联系是否紧密［15］。此方法研究的是少数据不确定性问题，对样本量的大小没有太高要求，因此剔除由于纤维板厚度、附加锚固措施和小尺寸梁导致公式不适用的几种情况，选取公式适用的32片梁作为研究对象。选取抗剪承载力序列[x0(k)]作为母因素序列，混凝土抗拉强度[x1(k)]、FRP极限强度[x2(k)]、FRP弹性模量[x3(k)]、FRP截面面积[x4(k)]、斜裂缝水平投影长度与FRP间距比值[x5(k)]，混凝土梁截面高度[x6(k)]作为子因素序列进行灰色关联分析。

GRA基本步骤：

①确定待分析序列。x0为母因素序列，xi为变量序列。

②序列无量纲化。计算公式为x′i(k)=xi(k)/-xi，其中

③求差序列、最大差和最小差。将无量纲序列代入Δi(k)=|x′0(k)-x′i(k)|中，得到各差序列Δi(k)，计算结果见表2。将数据代入和中求出最大绝对差Δmax和最小绝对差Δmin。

表2 无量纲处理后的数据序列和差序列

表3 各因素的灰色关联系数

⑤求灰色关联度γi。将得到的灰色关联系数εi(k)代入，计算各因素关联度。

各 因 素 的 关 联 度 为γ1=0.634 0、γ2=0.650 5、γ3=0.639 5、γ4=0.655 0、γ5=0.656 5、γ6=0.657 5。由此可见，6个因素对FRP梁加固后斜截面抗剪承载力提高值的影响由高到低依次为混凝土梁截面尺寸、斜裂缝水平投影长度与FRP间距比值、FRP截面面积、FRP极限抗拉强度、FRP弹性模量、混凝土抗拉强度。其中，混凝土抗拉强度虽然比其他因素影响较小，但影响程度接近，因此不能忽略混凝土抗拉强度对加固后斜截面抗剪承载力提高值的影响。由于规范并未考虑混凝土抗拉强度的影响，因此本文对公式进行修正。

3 斜截面承载能力计算公式的修正

3.1 混凝土抗拉强度对FRP梁抗剪承载力的影响

混凝土抗拉强度对加固后的抗剪承载力提高值有影响。当未采取有效的附加锚固措施时，FRP在主拉应力的作用下发生剥离破坏，粘贴界面处混凝土表现为内聚破坏。即FRP材料是因为界面处混凝土抗剪承载力补足而产生剥离破坏，故需要考虑混凝土强度的影响。因此，采用混凝土抗拉强度代替抗剪强度对加固后的抗剪承载力提高值进行修正。

在不同温度下，利用液体冷却介质处理玉米种子对玉米种子4 d和7 d发芽率有较大影响。同种种子在相同温度下用液体冷却介质处理不同时间后，其发芽率有显著区别。在-15℃下冷却介质处理不同时间的结果可以看出，X1，F6，S10，H1，H4和K16经液体冷却介质处理后，7d平均发芽率最高且均接近100%。液体冷却介质处理玉米种子是一种种子处理新技术。

若已对试验梁中抗拉强度标准值进行了测试，则采用实测值。对于无实测值的试验梁，采用JTG 3362—2018《公路钢筋混凝土及预应力混凝土桥涵设计规范》对抗拉强度标准值ftk进行近似计算，即

式中：fcu，k为混凝土的立方体抗压强度标准值；δ为混凝土的变异系数，可查规范；αc2为混凝土的脆性折减系数，对C40取1.00，对C80取0.87，中间按线性插值。

利用MATLAB的函数拟合功能对式（1）进行拟合修正，引入混凝土抗拉强度影响系数φc=0.348 2ftk+0.343 9来考虑混凝土抗拉强度对加固后斜截面抗剪承载力提高值的影响，即

试验梁抗拉强度标准值的计算结果见表4。可知，考虑混凝土抗拉强度影响系数后，除个别梁外，绝大部分梁修正后的FRP抗剪承载力贡献计算值明显更接近试验值。

表4 各试验梁的抗拉强度标准值的计算结果

3.2 采用纤维板对FRP梁抗剪承载力的影响

由于式（1）没有根据纤维板的性能特点进行计算，而是按多层纤维布进行强度折减，导致理论值与试验值偏差较大。因此，对纤维复合材料强度折减因子κm和有效粘贴长度Le进行修正。

当采用无附加锚固措施的碳纤维板进行抗剪加固时，κm取0.5。引入有效粘贴折减系数β，即

当碳纤维板厚度为1.4 mm时，β=0.7；当碳纤维板厚度为1.5 mm时，β=0.85。公式修正前后的计算结果见表5。可知，对κm和Le进行修正后，除7#梁外，其余梁修正后的FRP抗剪承载力贡献理论值明显更接近试验值。

表5 公式修正前后的计算结果

3.3 修正抗剪承载力公式验证

由于9#试验梁的加固方式为封闭式包裹，修正公式并未考虑这一加固方式对抗剪承载力贡献值的影响，因此，给出41片梁抗剪承载力试验值与计算值比值，见图2。图中，Vf，cal为抗剪承载力贡献计算值；Vf，exp为抗剪承载力贡献试验值。可见，修正后的梁抗剪承载力计算值与试验值的比值分布更加均匀，且接近1，说明利用修正后公式计算值更接近试验值，具有较高的精确度。

图2 41片梁抗剪承载力试验值与计算值比值

抗剪承载力贡献试验值与计算值对比见图3。其中，变化系数为计算值偏离试验值百分数的平均值p，p=(Vf，cal-Vf，exp)×100%/Vf，exp的平均值。可见，修正前后梁抗剪承载力贡献试验值与理论值之比的标准差由1.005减小为0.356，且均值由1.20减小为1.00，计算精度明显提高。

图3 抗剪承载力贡献试验值与理论值对比

4 结论

1）JTG/T J22—2008《公路桥梁加固设计规范》中纤维材料加固抗剪公式考虑的因素不全面，未考虑混凝土抗拉强度和新型纤维板材与纤维布差异性的特点，导致计算结果误差较大。

2）当梁体采用标高较高的混凝土时，规范公式的计算值偏小；当采用较厚的整体纤维板时，规范对纤维板的强度折减过大。

3）在规范推荐公式的基础上，引入混凝土抗拉强度影响系数，并且对纤维复合材料强度折减因子和有效粘贴长度进行修正；修正后，计算精度大幅提高，试验值与理论值之比的标准差由1.005缩小为0.356。

本文所选数据仅限于42根梁，且仅适用于未锚固、非全包裹的加固情况。今后对于抗剪承载力计算理论还需深入研究和优化。