大跨度公铁平层合建斜拉桥主梁有效宽度研究

2021-10-14李秀华任万敏曹海静

铁道标准设计 2021年11期

李秀华,任万敏,曹海静

(1.中铁二院工程集团有限责任公司,成都 610031； 2.中铁西南科学研究院有限公司,成都 610031)

大跨度公铁平层合建桥主梁常采用宽幅钢箱梁截面形式，钢箱梁具有抗弯能力强、抗扭刚度大、材料利用率高、造型优美等特点被广泛应用于桥梁工程中[1]。箱梁在弯曲横向力作用下，横向力通过腹板传递给顶底板，由于顶底板剪切变形的不均匀性，远离腹板的位置其纵向位移滞后于靠近腹板的位置，因此产生顶底板内弯曲法向应力的不均匀分布，称为剪力滞效应[2]。对于宽幅钢箱梁斜拉桥，主梁在弯矩、轴力的复合作用下，相比一般的简支、连续梁体系更为复杂，箱梁翼缘的剪力滞效应尤为突出。若忽略剪力滞效应的影响，可能导致结构局部应力超限，甚至产生桥梁结构的整体破坏[3]。

目前，国内外规范对于钢箱梁剪力滞效应并未统一，我国公路、铁路的桥梁设计规范均仅适用于纯弯构件，而斜拉桥由于拉索的作用，主梁为多点弹性支撑的压弯构件，规范中的计算方法并不适用[4]。斜拉桥规模较大，结构复杂，拉索和支座纵向分布对主梁剪力滞有明显影响和规律性，需要根据桥梁自身特点进行专门研究和设计。聂建国等研究了组合梁在轴向力作用下混凝土桥面板正应力分布情况及传递角度[5]。翟晓亮等提出了斜拉索水平轴向力作用下桥面板有效宽度系数沿跨长方向分布曲线计算公式，同时理论分析得出了弯矩作用下桥面板有效宽度系数的计算方法[6]。本文针对大跨公铁平层合建斜拉桥多点连续弹性支撑且同时承受轴力和弯矩的特点，通过建立全桥空间有限元分析模型，研究拉索轴力和成桥荷载作用下宽幅箱梁的法向应力分布，总结提出了斜拉桥全桥有效宽度分布规律。总体来看，跨中区、塔梁交汇区、辅助墩区有效宽度下降趋势明显，与现有研究成果结论相近，设计时应重点关注此类区域，通过加厚板厚、加劲构造等方式优化结构设计。

大跨度公铁平层合建桥具有跨度大、桥面宽、公铁共同作用荷载重等特点，与相近跨度的斜拉桥相比，同等索距下宽幅箱梁的弯曲剪力滞特性更为突出。加之高速铁路对结构刚度要求高，上行荷载较大，斜拉索索力随之增大，由此带来的拉索轴向力传递过程中，应力不均匀更为显著。因此，有必要针对大跨公铁平层合建斜拉桥主梁剪力滞效应开展深入研究。

1 项目概述

宜宾临港长江大桥于宜宾市临港区跨越长江，是新建川南城际铁路与渝昆高铁的过江通道，也是宜宾市规划的过江通道。为节约通道资源和工程投资，采用“四线铁路六车道公路”公铁两用桥梁方案。主桥按四线客运专线与六车道城市快速路同层设计，主桥梁长1 075.2 m，全桥孔跨可布置为9×40.7 m+(72.5+203+522+203+72.5) m+7×40.7 m，全桥立面布置见图1。

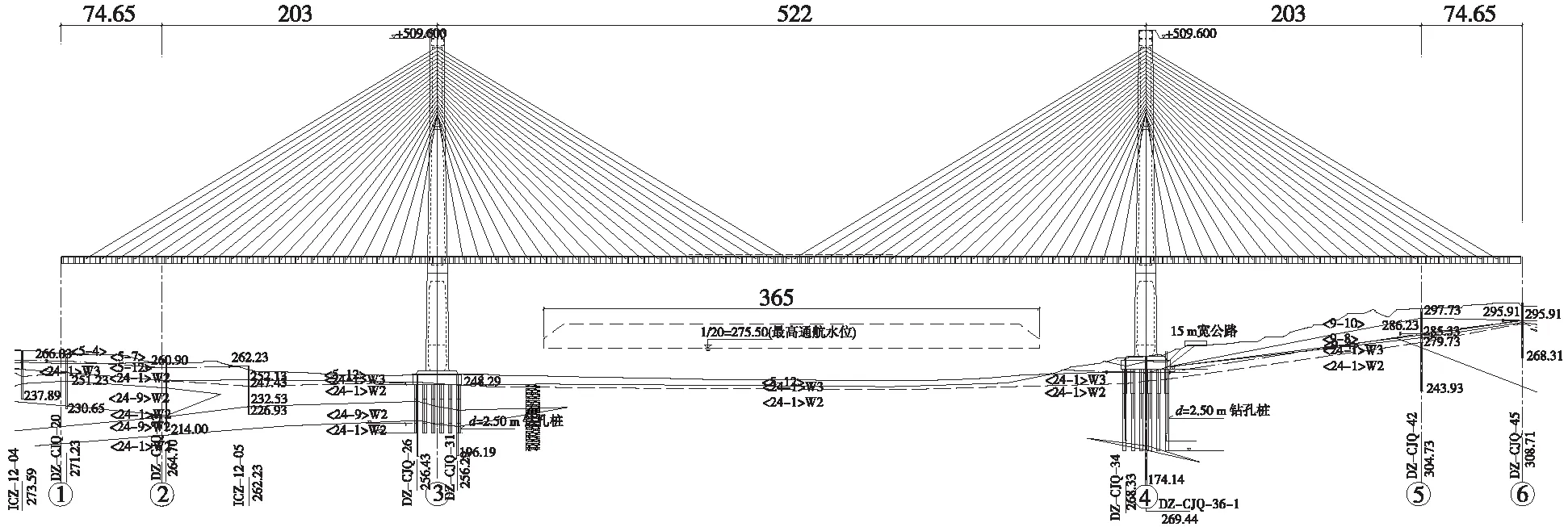
图1 全桥立面布置(单位：m)

主梁采用钢箱梁，桥面布置四线，300 km/h高速铁路设置在桥面中间，两侧各布置三车道设计速度80 km/h的城市主干道和人行道及非机动车道。桥宽63.9 m，采用国内首创公铁平层设计，为目前世界宽度最大的公铁两用桥，主桥桥面布置及钢箱梁断面见图2[7]。钢箱梁采用单箱五室结构，流线型轮廓，梁高5.0 m，主梁总宽63.9 m，底宽34.45 m。桥面设2%人字横坡，拉索锚固在铁路和公路之间，采用内置式钢锚箱，钢梁标准节段长12 m，单侧拉索采用2根索并置方案，拉索中心距0.9 m，顺桥向索距12 m。桥面布置见图2。

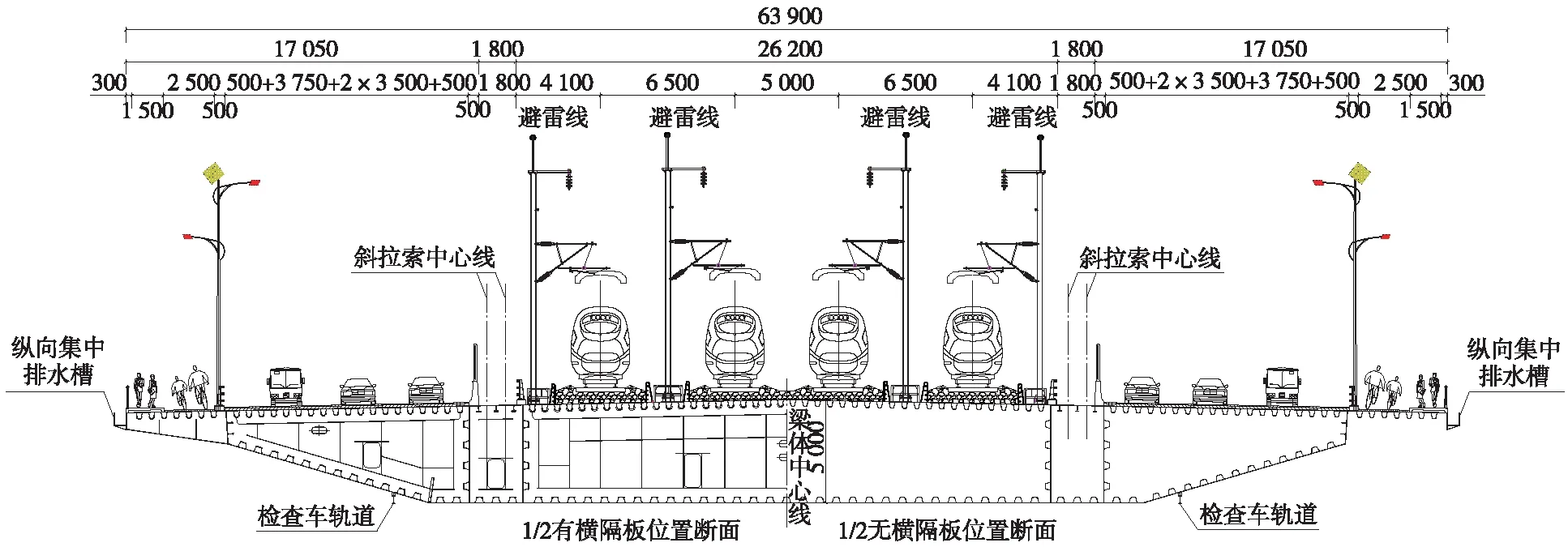
图2 钢箱梁桥面布置(单位：mm)

2 研究方法与模型建立

目前剪力滞效应的分析方法主要分为弹性力学解析法、比拟杆法、能量变分法[8]、有限元数值法和试验研究法等。基于理论的分析方法往往需要对复杂结构进行简化处理，对于钢箱梁斜拉桥这种大型复杂结构体系，采用理论分析得到的结果与实际情况差异较大。随着计算机技术的发展，基于板壳元的空间有限元方法成为了桥梁精细化分析的有效手段，通过建立全桥空间板壳单元模型，研究宽幅钢箱梁斜拉桥的传力路径和受力行为，分析剪力滞效应和分布规律。

主桥采用有限元软件Midas Civil建立空间有限元模型，主梁采用板单元模拟、主塔采用梁单元模拟、斜拉索采用桁架单元模拟，模型共有13 375个节点，24 768个单元。墩顶支座与主塔塔底采用一般支承模拟，塔梁间支座与索梁间采用弹性连接。全桥空间有限元模型如图3所示，基于该模型开展剪力滞效应分析。

图3 全桥空间有限元模型

采用该模型在成桥状态下非线性静力分析，研究恒载作用下钢梁顶底板的应力分布，进而求得恒载作用下有效宽度，计算公式如式(1)所示，有效宽度系数如式(2)所示[9]。

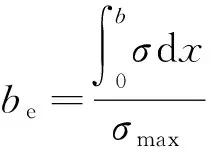
(1)

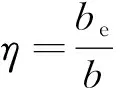
(2)

式中：be为钢箱梁顶板有效宽度；b为箱梁顶板宽度；σ为箱梁顶板正应力；σmax为箱梁顶板最大正应力；η为顶板有效宽度系数。

3 纵向力作用下有效宽度系数

3.1 各国规范传力规定

AASHTO LRFD规范[10]规定梁体在纵向集中力作用下，轴向力将沿两侧30°角方向传递，并逐渐均匀分布在整个桥面上，直至整个截面参与工作。German Deutsche Norm(DIN 1075)规范与之类似，角度为26.5°[11]。中国及欧洲国家等规范并未涉及轴向力作用下桥面有效宽度的问题。

3.2 拉索轴力作用下箱梁有效宽度

斜拉桥主梁为多点弹性支撑的压弯构件，主梁成桥计算结果包含有恒载弯矩和拉索轴力的综合影响，直接分析成桥结果很难分离拉索轴力影响结果。因此，国内外研究者常采用建立钢梁节段模型，在节段端部施加集中荷载，分析节段各截面应力分布的方式查看轴力作用影响的情况，研究结论与现有规范结果较为接近。

对于斜拉桥，斜拉索连续作用于梁体，多根拉索作用下箱梁应力分布与单独集中力效果不同。基于此，为研究斜拉索作用效果，可提取成桥状态下锚固点索力值，通过拉索倾角换算纵向水平分力，将该分力以集中荷载方式作用于锚固点位置，计算箱梁顶板应力。根据应力不均匀情况，按式(1)、式(2)计算有效宽度系数，绘制成桥状态(恒载)拉索轴力作用下全桥(半跨)有效宽度系数如图4所示。

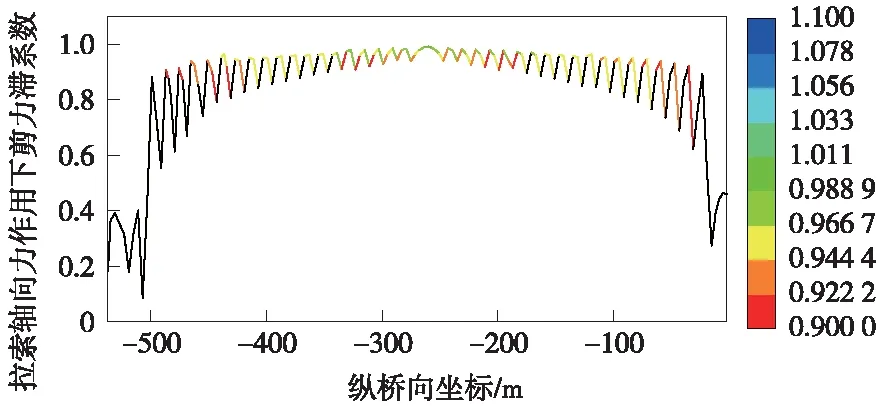
图4 拉索纵向水平力作用下有效宽度系数分布

图4中纵桥向坐标范围为小里程侧梁端至主跨跨中，坐标值为-537.6～0 m。从全桥有效宽度系数分布可以看出，受局部应力影响，最外侧拉索作用点(坐标-520 m、-20 m)处纵向力作用下箱梁应力不均匀程度最高，有效宽度系数为0.1～0.3，随着更多组拉索持续作用，应力扩散不断积累，应力分布逐渐均匀，箱梁有效宽度系数逐渐增大并趋于平稳，主塔位置(坐标-261 m)处有效宽度系数为1。

4 成桥状态主梁有效宽度

4.1 关键截面应力横桥向分布

在成桥状态下主梁受轴力、弯矩的共同作用，箱梁顶板纵向应力出现明显的不均匀现象[12]。为计算顶板应力不均匀的变化规律，通过空间有限元模型成桥计算，确定主梁恒载、主力工况作用下关键截面钢箱梁顶、底板纵向正应力沿横桥向分布情况[13]，公铁活载以车道面方式加载[14]。边跨跨中箱梁顶(底)板纵向正应力分布见图5、图6，桥塔位置箱梁顶(底)板纵向正应力分布见图7、图8，主跨跨中箱梁顶(底)板纵向正应力分布见图9、图10，辅助墩位置钢箱梁顶(底)板纵向正应力分布见图11、图12。

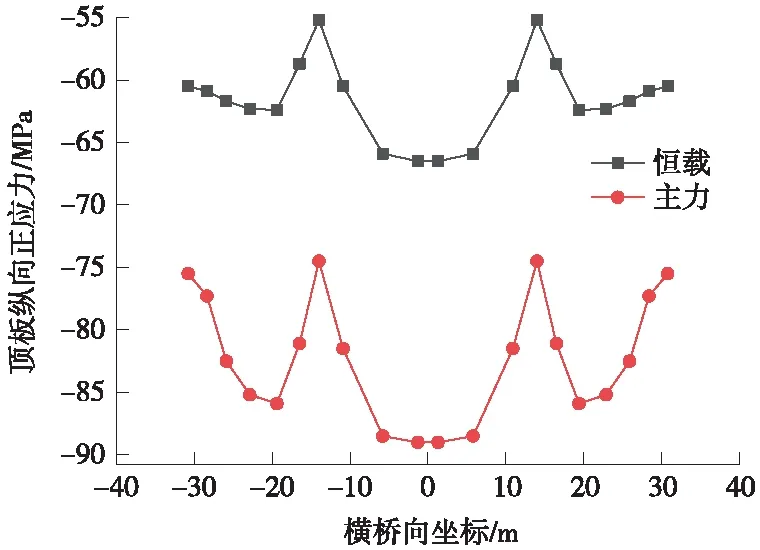
图5 边跨跨中箱梁顶板纵向正应力

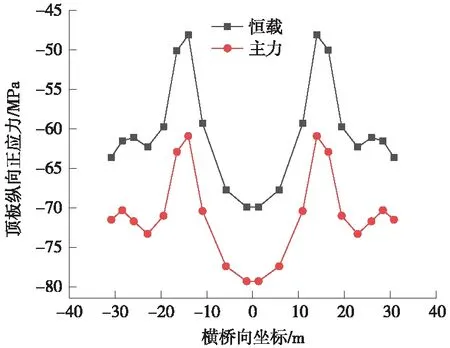
图7 桥塔位置箱梁顶板纵向正应力

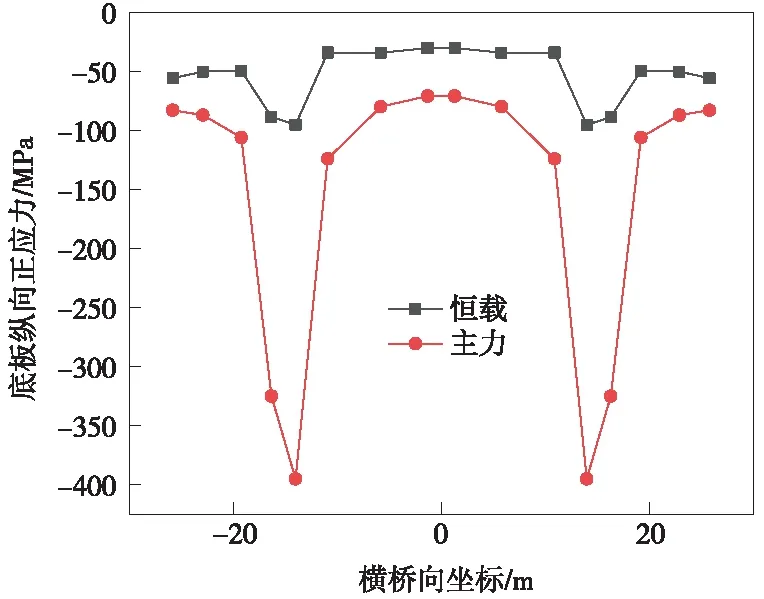
图8 桥塔位置箱梁底板纵向正应力

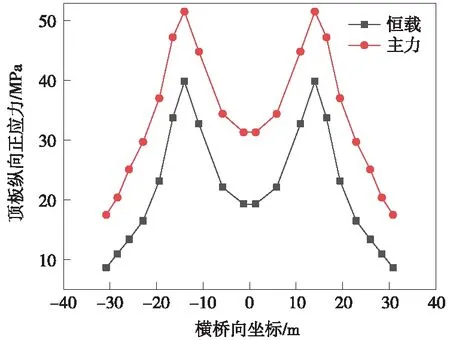
图9 主跨跨中箱梁顶板纵向正应力

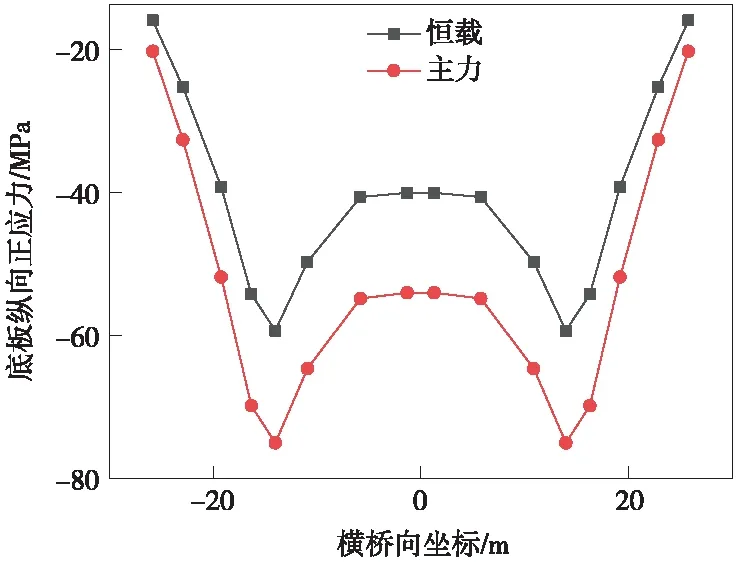
图10 主跨跨中箱梁底板纵向正应力

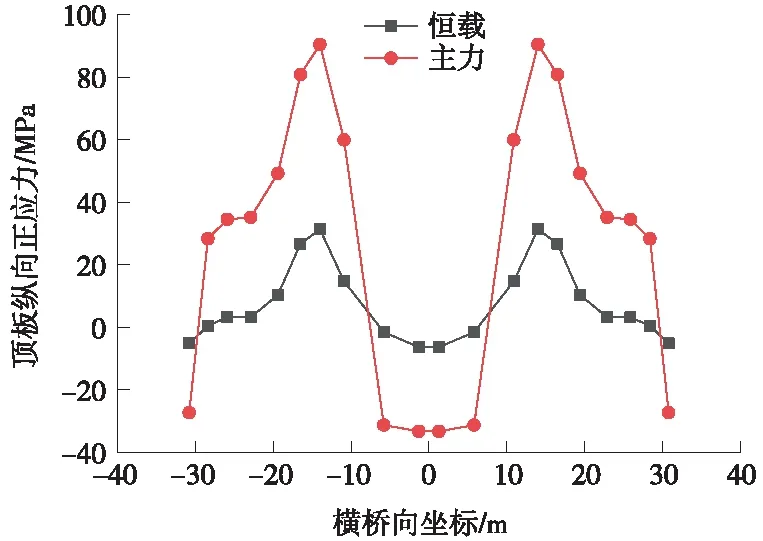
图11 辅助墩位置钢箱梁顶板纵向正应力

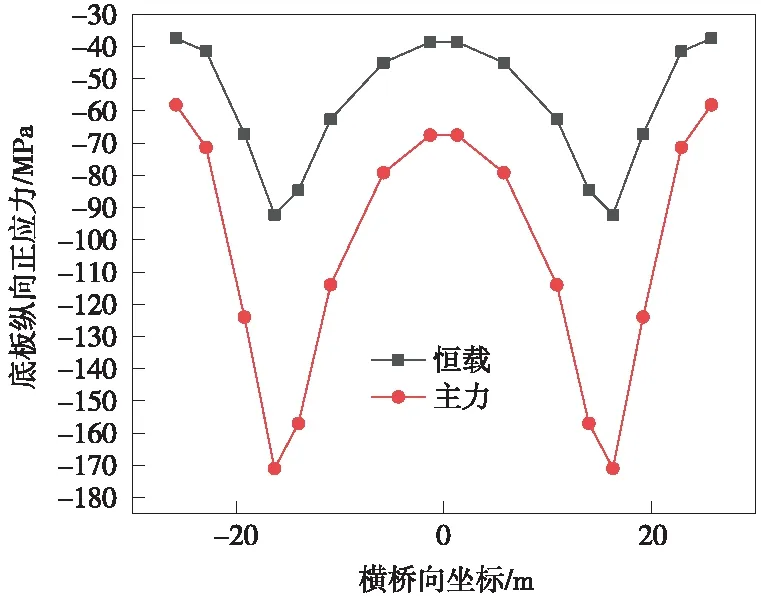
图12 辅助墩位置钢箱梁底板纵向正应力

根据图5～图12所示，钢箱梁顶底板的纵向应力沿横向分布应力相差不明显，全桥典型位置处均呈现锚箱位置处应力较大，横向跨中及两翼应力较小的趋势[15]。主力工况与恒载工况纵向应力的横向分布变化趋势一致。

由以上分析可知，边跨跨中、桥塔位置顶板纵向为压应力，主跨跨中顶板纵向应力为拉应力，辅助墩区域由于主梁负弯矩及拉索轴力的作用，呈现部分受拉，部分受压的状态，应力不均匀程度虽然较高，但应力水平满足规范要求。无论顶板内纵向应力为拉压状态，在横向分布均呈现拉索作用位置附近较大的趋势，可知宽幅钢箱梁纵向主要经由拉索锚箱及纵腹板传力[16-17]。全桥底板纵向为压应力，桥塔底板应力出现应力集中，因为该处为支座位置的缘故，因本模型未考虑支座位置处加劲加强处理[18]，故该处应力超限不反映真实情况，应由支座位置局部分析确定。

本桥边跨跨中、桥塔、主跨跨中等位置处顶板应力主力与恒载工况之比为1.1～1.3，而辅助墩位置主力与恒载比值达到2.89，辅助墩位置活载作用占比明显，且应力相对其他区域较大。因此，应着重考虑辅助墩区域顶板设计。

对于底板，边跨跨中主力与恒载应力整体应力水平相差较大，最大应力比值为92/52.8=1.74。辅助墩位置处最大应力比值为171/92.2=1.85，辅助墩区域应力相对集中于支座位置处。成桥状态下底板应力水平沿全桥(除支座附近外)基本一致，均在40～60 MPa以内，支座位置处应力水平较大，因此应根据应力分布合理确定底板板厚及分布。

4.2 钢箱梁顶底板有效宽度

根据应力不均匀情况，按式(1)、式(2)计算有效宽度系数，绘制半个桥跨(对称)的顶底板有效宽度系数如图13、图14所示。

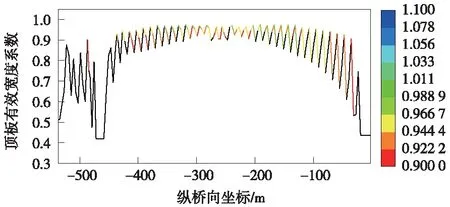
图13 主梁顶板有效宽度系数全桥分布

图14 主梁底板有效宽度系数全桥分布

从图13、图14分析可知，顶板有效宽度系数最小为辅助墩顶处，其值为0.43，说明该截面处剪力滞效应最严重。索塔支座附近的剪力滞效应次之[19]。跨中附近的剪力滞效应较前两者小，其有效宽度比为0.5。其余几处断面的剪力滞效应最小，有效宽度比基本在0.92左右，总结原因为弯矩作用下主跨跨中有效宽度系数最大，且在较长区域内均匀分布。轴力作用下主跨跨中有索区段内有效宽度系数沿跨长方向呈线性变化，有索区越靠近边索有效宽度系数越小。底板有效宽度分布与顶板情况类似，由于桥塔支座局部应力集中等影响，桥塔位置处有效宽度折减更为明显。以上规律符合斜拉桥钢箱梁压弯构件的受力特点[20]。相比拉索轴力作用成桥状态下有效宽度系数受弯矩作用影响突出，主梁在塔梁交汇处、辅助墩墩顶位置处有效宽度系数明显下降。