基于增广P型学习观测器的航天器故障重构和自适应容错控制

骆天依 李化义 孟庆松

0 引言

姿态控制系统作为航天器最重要的子系统之一,由于所处空间具有复杂不确定性,极易发生故障,导致航天器失去稳定性甚至完全失效[1-3]．因此,很有必要对航天器发生的故障及时进行诊断和隔离,并设计出新的容错控制器保证航天器在轨运行期间的可靠性与安全性．

按照Frank等[4]的观点,故障诊断方法可以分为三类:基于解析模型的方法、基于信息处理的方法和基于知识的方法．其中,基于解析模型的方法作为传统的故障诊断方法,经过近50年的发展和完善,至今仍被广泛应用在航天器姿控系统故障重构和容错控制领域．然而随着航天任务难度的提升,航天器的结构和功能趋向于复杂多样化,构成航天器的元器件种类和数量不断增加,这也提高了故障诊断方法的复杂性和容错控制器的设计难度．但仍有很多学者在此领域进行着不断的探索和突破．

针对航天器执行机构故障,Li等[5]设计了扩张状态观测器对航天器姿控系统模型参数、外在干扰和执行器的饱和输出进行估计和补偿,并利用逆最优控制李雅普诺夫函数方法保证闭环系统的渐近稳定性;Zhang等[6]针对刚性航天器执行机构失效故障和饱和约束,设计了一种滑模故障估计观测器,并在此基础上利用滑模控制思想设计了相应的容错控制器;Wang等[7]首先利用自适应方法估计执行器故障模型中的未知参数,在此基础上设计出一种自适应未知输入观测器对故障进行检测和隔离．

针对航天器传感器故障,Wang 等[8]基于线性矩阵不等式技术设计出两组具有良好鲁棒性的H∞最优观测器,并设计出满足一定姿态误差精度的PD控制器(Proportional-Derivative controller)保障航天器在陀螺和传感器故障同时发生情况下的安全稳定运行能力;韩冰[9]对基于扩张状态观测器的方法进行了改进,并利用动态输出反馈的方法,提高了故障系统的控制性能;江耿丰等[10]对常用的卫星测量部件光学敏感器和惯性敏感器分别设计了隔离观测器和Kalman滤波器,通过比较两个观测器的输出残差,达到故障诊断和隔离的目的．

基于上述研究,本文提出了一种基于增广P型迭代学习观测器的航天器传感器故障重构方法,并利用自适应积分滑模的思想设计新的控制器,解决了对航天器姿控系统故障容错控制问题．最后,通过航天器姿控系统仿真实例验证了本文所设计观测器和控制器的有效性．

1 问题描述

1.1 航天器姿控系统模型

考虑如下三轴稳定刚体卫星的姿态运动学与动力学模型:

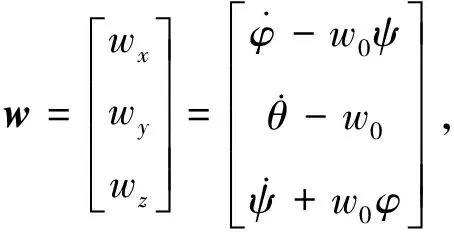
(1)

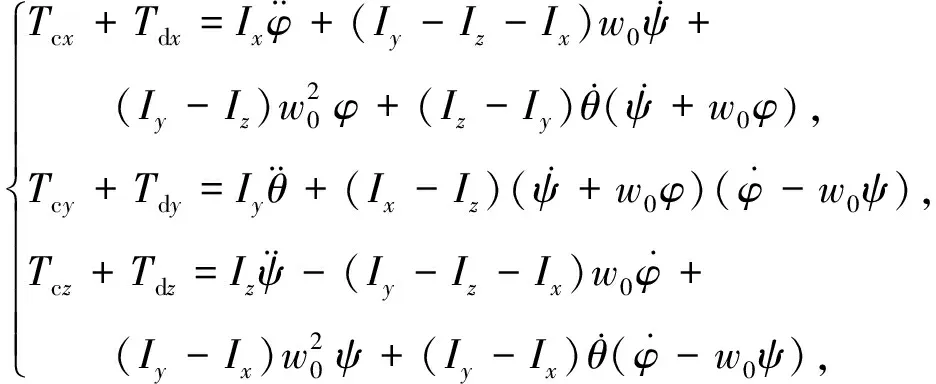
(2)

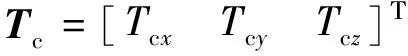
定义

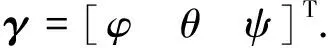
(3)

忽略二阶小量对系统模型的影响,动力学模型可以转换成如下微分方程的形式:

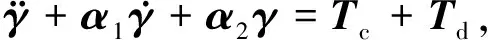
(4)

其中参数矩阵α1和α2表示如下:

令

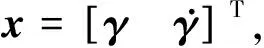
(5)

能够得到如下形式的航天器姿控系统状态空间模型:

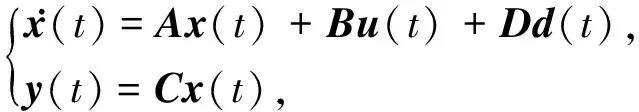
(6)

其中u(t)=Tc表示控制输入,d(t)=Td表示干扰输入．

1.2 问题描述

现考虑如下含有不确定干扰输入的传感器故障模型:

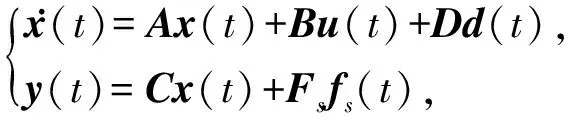
(7)

其中x(t)∈Rn,u(t)∈Rm,y(t)∈Rr分别表示系统状态向量、输入向量和输出向量，fs(t)∈Rq和d(t)∈Rr0分别表示航天器陀螺仪故障和受到的未知干扰，A,B,C,D均为适当维数的系数矩阵,A∈Rn×n,B∈Rn×m,C∈Rr×n,D∈Rn×r0,且满足r0≤r．

对于式(7)所示的传感器故障,为了抑制故障输出对系统可靠性的干扰,可以设计如下形式的输出滤波器:

(8)

其中系数矩阵Az∈Rr×r是一个稳定矩阵,所有特征值均具有负实部．

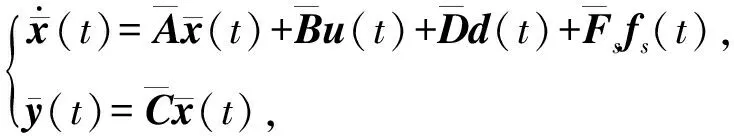
(9)

其中

本文的目的之一就是针对传感器故障增广系统(9)设计增广P型学习观测器,使得传感器故障能够实现精确重构．

同时,为了改善故障系统的性能指标,减轻陀螺仪故障对航天器姿控系统的不利影响,本文在实现故障重构的基础上,基于故障模型(7),进一步设计容错控制器,保证航天器在故障状态下的稳定运行能力．

2 基于增广P型学习观测器的故障重构

针对传感器故障增广系统(9),考虑如下形式的增广P型学习观测器:

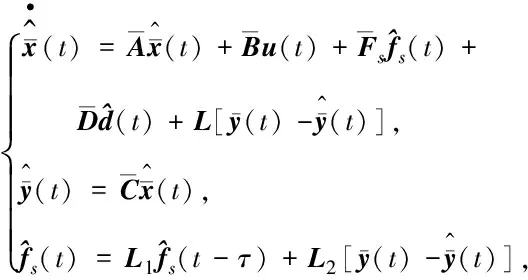
(10)

定义几种误差变量如表1所示．

表1 增广P型观测器设计所需误差变量

考虑增广系统(9)及其增广P型学习观测器(10),根据表1,可得误差系统动态方程:

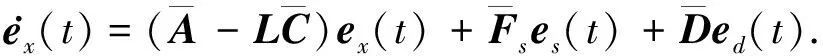
(11)

给出以下假设辅助增广P型故障重构观测器的设计:

(12)

根据假设1和表1,能够得到如下传感器故障重构误差方程:

(13)

引理1[11]若传感器故障重构误差如表1所示,则有以下不等式:

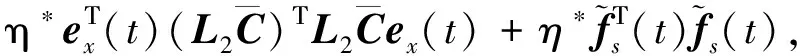
(14)

其中η*在定理1中给出．

定理1对于增广系统(9)及其增广P型学习观测器(10),若存在下列不等式,则所设计的增广P型学习观测器能够使系统状态估计误差ex(t)、干扰估计误差ed(t)和传感器故障重构误差es(t)一致渐近稳定．

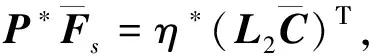
(15)

(16)

(17)

其中矩阵P*,Q*,参数δ*,ε*,η*,μ*的定义在证明过程中给出．

证明构造Lyapunov函数

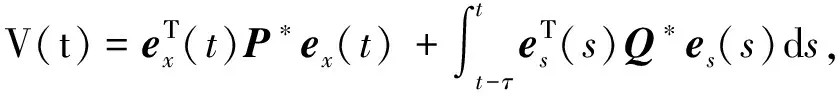
(18)

其中P*∈Rn,Q*∈Rm为正定的实对称矩阵．

将式(18)对时间t求导,得到:

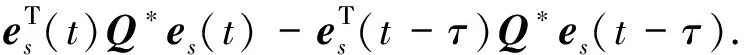
(19)

引理2[12]设x,y是具有适当维数的实向量,A,B(t)是具有适当维数的实矩阵,‖B(t)‖≤r,存在任意正数ε,有

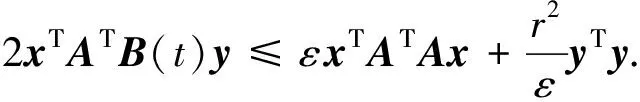
(20)

根据引理2,有:

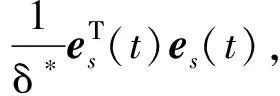
(21)

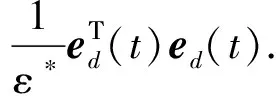
(22)

将式(21)和式(22)代入到式(19)中,并借助引理1,得到:

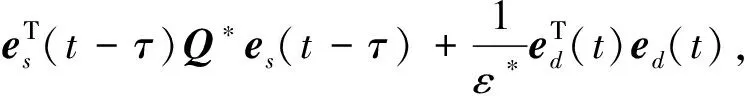
(23)

其中

η*=(1+σ*)λmax(Q*),

σ*≥0.

将式(13)代入式(23),并化简得到:

(24)

对于式(24),如果定理1中的式(15)成立,则有:

(25)

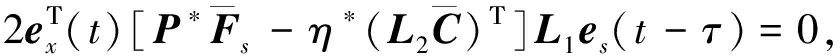
(26)

(27)

将式(25)—(27)代入到式(24)中,得到:

(28)

根据引理2,有:

(29)

将式(29)代入到式(28)中,有以下不等式成立:

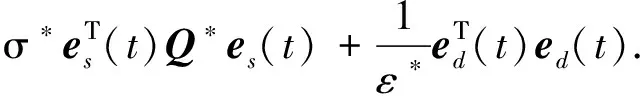
(30)

根据定理1中式(16)和式(17)可知:

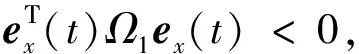
(31)

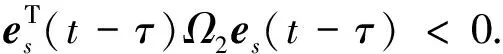
(32)

所以有:

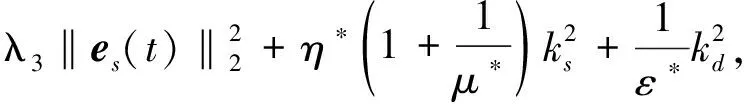
(33)

其中

将式(33)进一步简化,得到:

(34)

其中

根据式(34)可知,当不等式满足

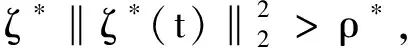
(35)

能够得到:

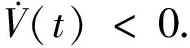
(36)

根据Lyapunov稳定性理论,系统状态估计误差ex(t),干扰估计误差ed(t)和传感器故障重构误差ed(t)一致渐近稳定．定理证毕．

由于定理1求解较为复杂,为计算定理1中的式(15)—(17),给出以下引理:

引理3[13]设

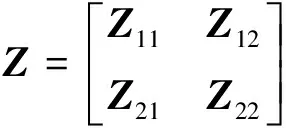
(37)

为对称阵,则Z>0的充要条件是:

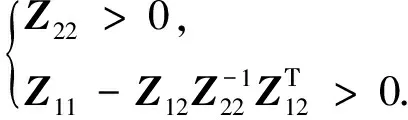
(38)

引理4[14]对于给定矩阵A∈Rn,当且仅当存在对称矩阵P∈Rn满足

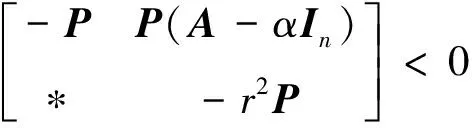
(39)

时,矩阵A的所有特征值能够位于圆形稳定域D(α,r)内．其中α和r分别表示该稳定圆的圆心和半径．

利用引理3和引理4,将式(15)—(17)转换为线性矩阵不等式形式:

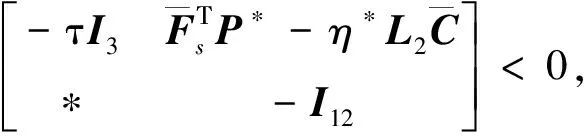
(40)

(41)

(42)

其中α和r分别表示该稳定圆的圆心和半径．

至此,增广P型学习观测器设计完成．

3 基于自适应积分滑模的主动容错控制

令

(43)

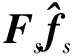
定义如下形式的积分滑模面:

(44)

其中矩阵K*=(CB)+∈R3×6,yc(t0)表示系统初始时刻的实际输出．采用这种积分滑模面可以使系统快速到达滑模面,提高系统的鲁棒性能．

对积分滑模面(44)求导,得到:

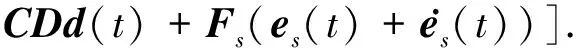
(45)

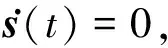
ueq(t)=-B+(A+I)x(t)-B+Dd(t)-

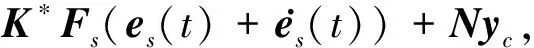
(46)

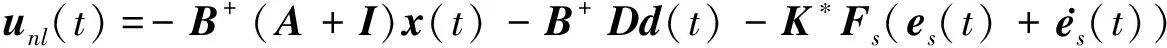
将等效控制律(46)代入到系统(7)中,得到如下形式的积分滑模状态方程:

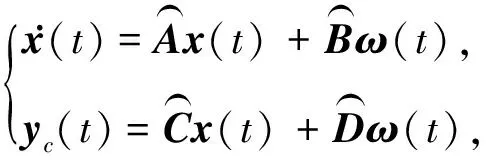
(47)

其中

定理2对于传感器故障系统(7),设计形如式(48)所示的容错控制律,能够保证系统的渐近稳定性．

u(t)=unl(t)+ul(t),

(48)

其中

其中λ*是选取的正常数．

被估计的未知参数ρ表达式为

(‖K*NFs‖+‖K*Fs‖)‖es(t)‖,

(49)

其自适应律为

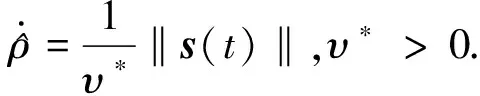
(50)

为求解定理2中的输出反馈增益矩阵N,给出以下辅助引理．

引理5[15]对于形如式(51)的线性系统,若存在正定对称矩阵P使得式(52)成立,则线性系统(51)渐近稳定．

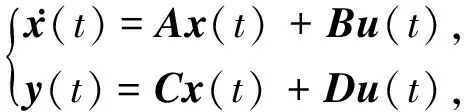
(51)

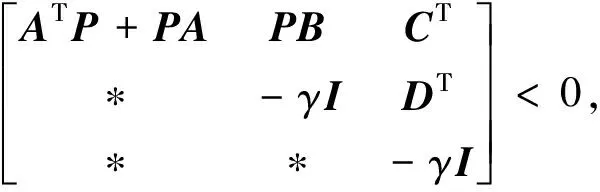
(52)

其中γ为一个任意给定的正常数,I为适当维数的单位阵．

证明首先,对于航天器姿控系统陀螺故障情况下的状态空间模型(47),利用引理5能够得到形如式(53)所示的不等式,使得系统(47)渐近稳定．

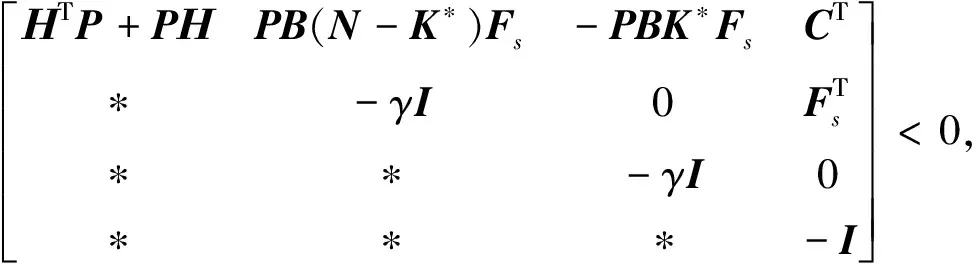
(53)

其中H=BNC-I．矩阵P和N可以通过LMI工具箱求解得到．

然后,定义形如式(54)的Lyapunov函数,利用Lyapunov稳定性理论,证明整个系统在故障重构后的渐近稳定性．

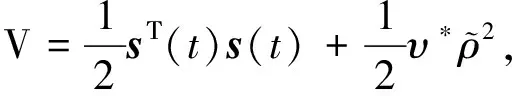
(54)

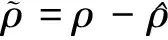
sΤ(t){[K*C(A+I)+NC]x(t)+

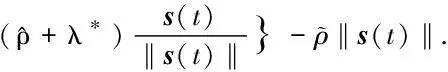
(55)

假设系统受到的未知噪声干扰有界,即‖d‖≤d0．进一步有:

(‖K*NFs‖+‖K*Fs‖)‖es(t)‖+

‖B+D‖d0]·‖s(t)‖≤

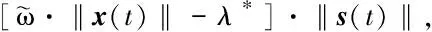
(56)

其中

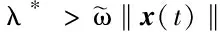
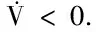
(57)

根据Lyapunov稳定性理论可知,所设计的自适应滑模容错控制器能够保证航天器姿控系统在陀螺仪故障情况下的渐近稳定性．

4 仿真实例

令δ*=ε*=1,Q*=L1=I3,此时有λmax(Q*)=1,η*=1．选取圆形稳定域D(0,1),学习速率τ=0.001,并选取如下参数矩阵:

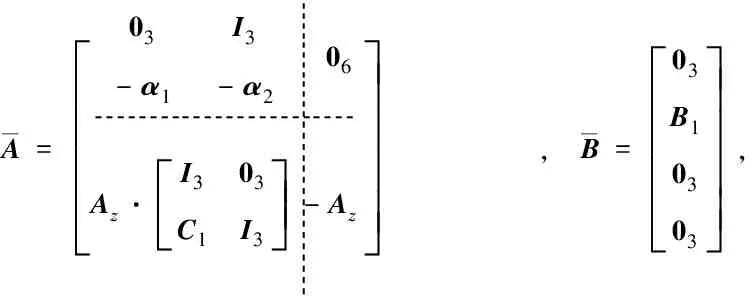
A=éëêêêê03I3-α1-α206Az·I303C1I3éëêêùûúú-Azùûúúúú, B=03B10303éëêêêêùûúúúú,

其中：

Az=diag{-1,-1,-1,-1,-1,-3},

w0=0.001 rad/s,

Ix=12.49 kg·m2,

Iy=13.85 kg·m2,

Iz=15.75 kg·m2,

利用LMI工具箱feasp求解器求解不等式(55)、(56)和(57),得到观测器增益矩阵L和L2分别为

根据以上给出的仿真参数和增益矩阵,可以利用Simulink搭建航天器姿控系统增广P型学习观测器．三种常见故障类型的仿真结果如图1—3所示．

图1 滚动轴陀螺加性突变故障重构Fig.1 Fault reconstruction of rolling axis gyro with additive sudden change fault

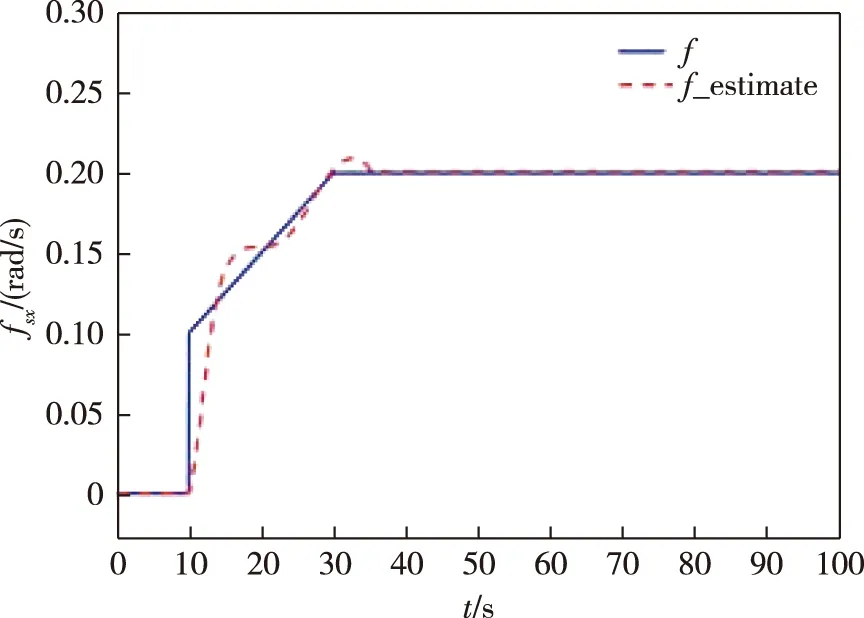
图2 滚动轴陀螺加性时变故障重构Fig.2 Fault reconstruction of rolling axis gyro with additive time-varying fault

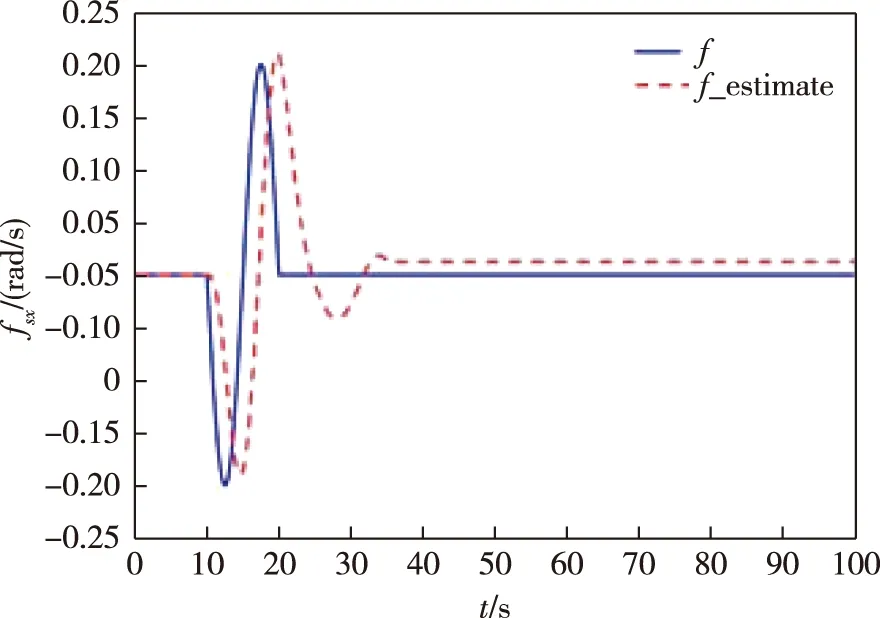
图3 滚动轴陀螺加性正弦时变故障重构Fig.3 Fault reconstruction of rolling axis gyro with additive sinusoidal time-varying fault

1)滚动轴陀螺仪发生加性突变故障:

2)滚动轴陀螺仪发生加性时变故障:

3)滚动轴陀螺仪发生加性正弦时变故障：

从图1—3可以看出,采用增广P型学习观测器能够对以上三种类型的传感器故障实现重构,验证了算法的可行性．但可以看出,这种故障估计方法对故障的估计有时不够精确．在故障突然发生时,对故障信号的响应不够及时;在故障消失或稳定后,仍存在一定的估计误差．可见该观测器对缓变故障的重构效果较好,对陡变故障的重构效果较差．

接下来,利用定理2设计自适应主动容错控制器提高故障系统的稳定性．

首先,利用Matlab/LMI工具箱feasp求解器求解不等式(50),得到矩阵P和N．然后选取参数λ*=υ*=1,同时假设在t0时刻yc(t0)=0．

假设滚动轴陀螺发生如下形式的加性正弦时变故障:

采用传统PD控制器和采用本文所设计的容错控制器的仿真结果如图4—7所示．

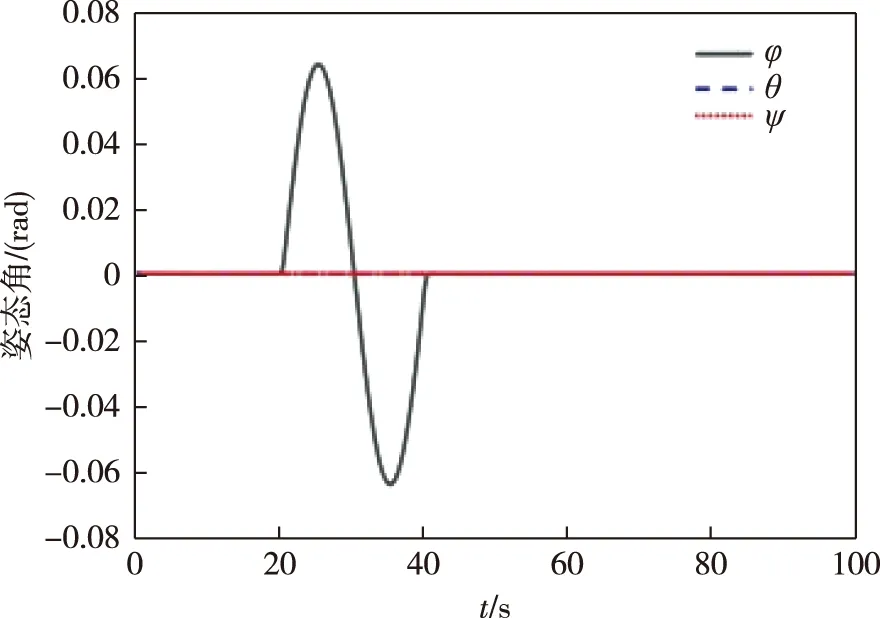
图4 陀螺加性正弦时变故障情况下传统PD控制器姿态角控制效果Fig.4 Attitude angle control effect of traditional PD controller under additive sinusoidal time-varying fault of gyro

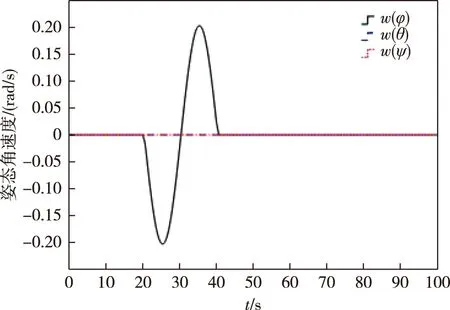
图5 陀螺加性正弦时变故障情况下传统PD控制器姿态角速度控制效果Fig.5 Attitude angular velocity control effect of traditional PD controller under additive sinusoidal time-varying fault of gyro

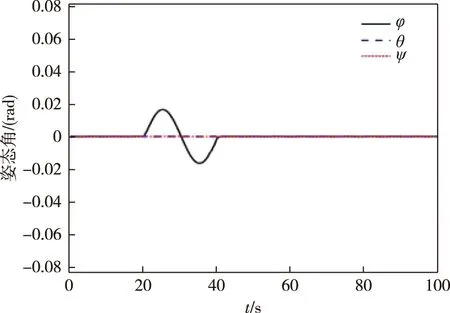
图6 陀螺加性正弦时变故障情况下自适应滑模容错控制器姿态角控制效果Fig.6 Attitude angle control effect of adaptive sliding mode controller under additive sinusoidal time-varying fault of gyro

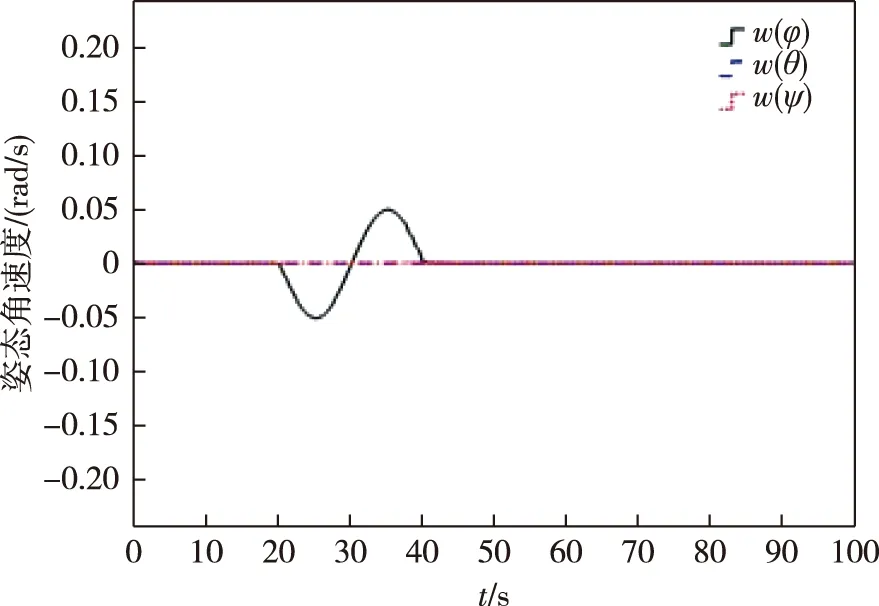
图7 陀螺加性正弦时变故障情况下自适应积分滑模容错控制器姿态角速度控制效果Fig.7 Attitude angular velocity control effect of adaptive sliding mode controller under additive sinusoidal time-varying fault of gyro

对比观察图4—7可以看出,在采用自适应积分滑模容错控制器后,航天器滚动轴姿态角和姿态角速度在相同的故障时间内变化幅度减小．其中姿态角变化范围大致从±0.065 rad变化到了±0.015 rad,姿态角速度变化范围大致从±0.19 rad/s变化到了±0.05 rad/s,系统的稳定性有了明显的改善．这可以说明积分滑模能够提高系统的鲁棒性,同时能够验证所设计自适应滑模主动容错控制器的有效性．

5 结论

本文提出了一种能够在线估计航天器姿控系统传感器故障的增广P型学习观测器.在将传感器故障等效考虑成伪执行器故障后,将故障值近似看作与前一时刻故障估计值和当前时刻输出估计误差有关的两项,实现了对未知传感器故障的重构．在此基础上,基于自适应技术和滑模理论,设计自适应主动容错控制器,并利用Lyapunov稳定性理论对改进后的模型进行了稳定性分析．仿真结果可以说明本文所设计的P型学习观测器和自适应容错控制器均满足系统设计要求．