基于SVM-BP神经网络的气象能见度数据缺失值预估
2021-10-14殷利平刘宵瑜盛绍学温华洋邱康俊
殷利平 刘宵瑜 盛绍学 温华洋 邱康俊
0 引言
为了将气象研究对社会的积极作用融入到公共服务中,中国气象局于2002年投资建设“三站四网”的大气监测工程,在全国各地陆续建立自动气象站.这些自动气象站引进许多高精度的气象观测设备,大大提高了对气象要素进行实时探测的能力[1-2].安徽省大多数气象站采用散射式能见度仪采样,但是在日常工作中能见度仪会出现采样数据缺失的情况,一般由以下几种情况造成:1)能见度仪的镜头前或两个镜头之间有异物堵塞,如蜘蛛结网、小鸟做窝等;2)在一些施工区,或省道县道等公路旁,灰沙和扬尘可能导致能见度采样区内颗粒物变化不定;3)恶劣天气下,局部地区的风速、风向变化大且快,导致树叶、杂物被吹起恰好位于能见度仪的采样区内,雨雪天气和天气寒冷凝结的冰霜也可能使能见度仪镜头表面受污染严重,导致能见度数据不准确;4)传感器各接线端出现接触不良、松动,以及传感器的某一单元模块发生故障、仪器年久失修得不到有效的维护等情况[3-4].有些自动气象站建立在高山丘陵地带,人工维护难度大、成本高,迫切需要一种既可以及时得到气象站所测的完备气象信息,又可以减轻工作人员对问题气象站进行维护的工作量的方法.
目前,处理能见度仪数据缺失的方法主要可以分为基于统计的修补算法、基于邻近性的修补算法、基于机器学习的修补算法三大类.基于统计的修补算法包括均值插补[5]、回归插补[6]、多重插补[7]等,其中均值插补以数据序列的平均值作为填充缺失值;回归插补是把缺失属性作为因变量,其他相关属性作为自变量,利用它们之间的关系建立回归模型来预测缺失值的;多重插补是用一组近似值替换每个缺失值,再用标准的统计分析过程对多次替换后产生的若干数据进行分析、比较,从而得到缺失值的估计值.基于统计的插补方法虽然简单易操作,但容易扭曲数据分布,且该类算法需要预先知道数据分布特征,但很多实际应用场景中却无法得到.基于邻近性的修补算法中最具有代表性的是K近邻算法(K-Nearest Neighbor,KNN)[8-9].K近邻算法首先要找出数据集中与缺失数据的欧式距离最小的K个点,然后用这K个点的平均值替换缺失值,其修补效果易受到邻近阈值的影响,且容易受到噪声数据的干扰,若对数据集未做初步预处理,修补精度容易产生较大的偏差.基于机器学习的修补算法能够直接处理缺失数据,并对缺失数据集进行训练,该类方法的优点是可以直接处理完全随机缺失模式下的数据集.该类算法主要包括:集成方法(以神经网络集成方法为主)[10]、多层感知机插补[11]、决策树、贝叶斯[12-13]、支持向量机(Support Vector Machine,SVM)[14-15]等,其中集成方法修补缺失数据以BP神经网络应用最为广泛.BP神经网络是指利用误差逆传播(Error Back Propagation)算法训练的多层网络,BP算法是将误差反向传播使神经元各层权值不断调整,直到网络输出的误差减少到可接受的程度,其优点是在处理不完整大规模数据时速度快、泛化能力强.SVM也是一种通用的机器学习算法,它以统计学习理论为基础,广泛应用在函数回归、时间序列预测等领域[16-17].SVM算法首先是通过非线性映射函数把样本向量映射到高维特征空间,使得在特征空间中,原空间数据的像具有线性关系,然后在特征空间中构造线性最优决策函数,从而解决分类与回归问题.在处理缺失值回归分析时,SVM算法可以修补任意缺失模式的数据,减少计算复杂度[18].
本文利用机器学习的相关算法在缺失值插补方面的优异性,综合运用SVM和BP神经网络预估能见度缺失值.首先选用安徽气象局历年来不同地区气象站的历史数据进行分析,然后建立数据填充模型,再运用权重优化不同模型对缺失值的预估值.实验结果表明,运用组合模型对不同地形的能见度缺失数据进行预估,预估结果可以有效地代替真实值,实现了对自动气象站的缺失数据的高精度填补.
1 数据的来源和模型构建
1.1 数据处理
本文中气象数据全部来自安徽气象局历年来汇总的气象站观测资料.如图1所示,安徽地形复杂多样,不同地形气候不一,因此所得到的观测数据差值较大.考虑到地形因素对模型处理缺测数据的影响,本文以高山、山谷、平原、水源地地形作为特征,分别选取黄山站(高山地形)、山南溪谷站(山谷地形)、灵璧站(平原地形)和白泽湖站(水源地地形)的历史数据进行试验(图2).早期的自动气象站由于设备质量参差不齐,传感器检测精度低,得到的数据不完整.为了保证数据的有效性,本文选取从2015—2019年安徽省气象局记录较为完整的小时时序数据资料作为总样本.对于每种地形,将相应的样本分为10个样本集,其中7个样本作为训练集,3个样本集作为验证集.测试集选取各站点2019年春季3—4月小时观测资料,一些时间区间内如果能见度数值变化较小,选取的数据量也相应减少.
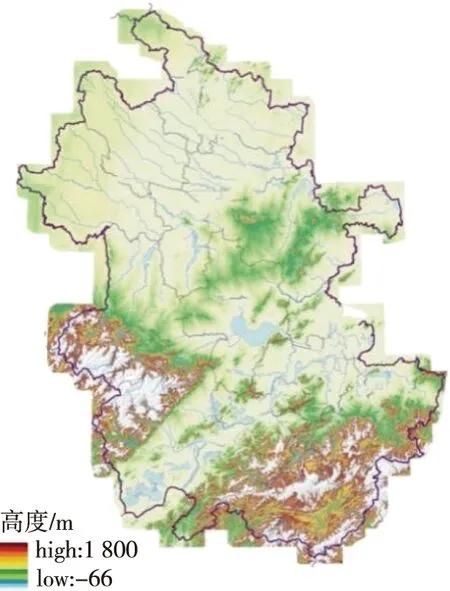
图1 安徽省地形图Fig.1 Topographic map of Anhui Province
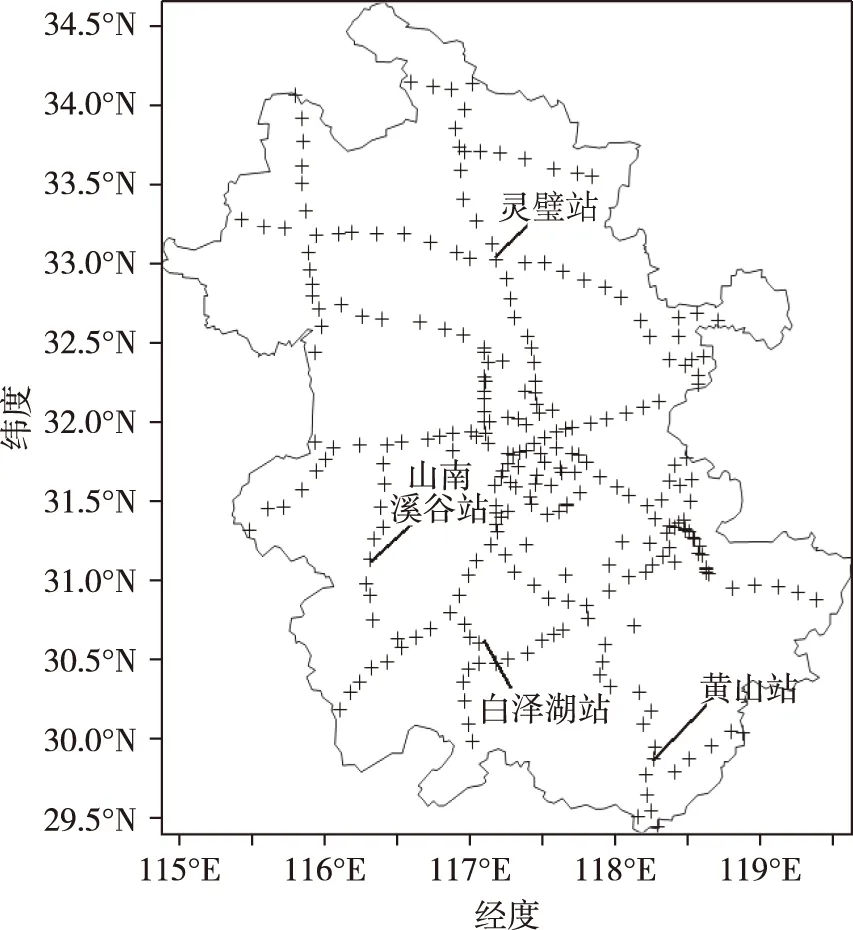
图2 安徽省各区域小型气象站分布Fig.2 Distribution map of meteorological stations in Anhui Province
1.2 输入要素的选择
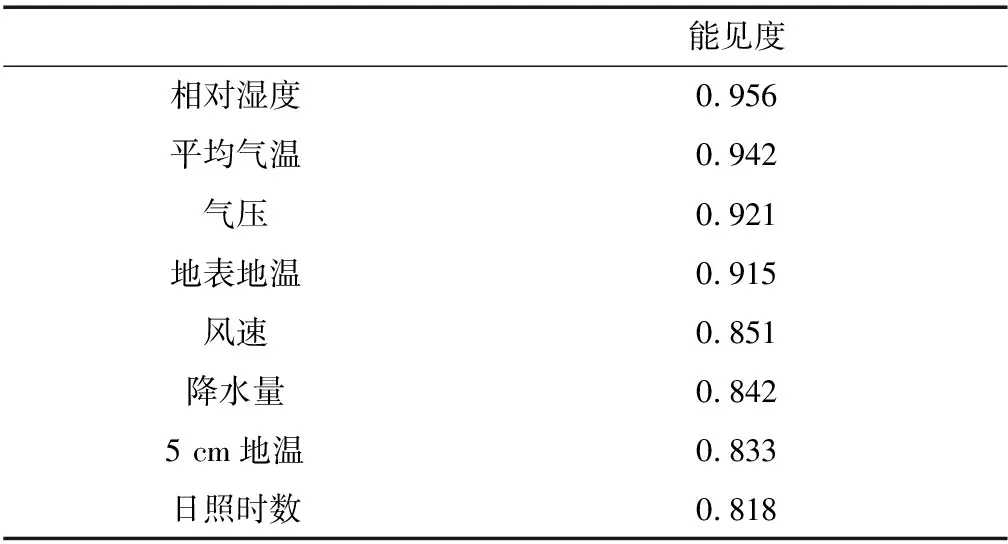
气象观测要素很多,有些气象观测要素对能见度的影响很小,如果将一个时序的全部观测要素作为输入不仅计算量大,而且会影响预估结果的准确性.人为筛选输入要素的方法具有很大的主观性,缺乏理论依据,因此本文选用灰色关联分析法进行输入变量的选择[19-20].该方法是根据各因素之间数值变化趋势的程度来确定关联大小,这种方法对数据要求较低,步骤清晰且计算量小.灰色关联法中一个重要指标是灰色关联度,灰色关联度以数值的形式表征各变量间关系的强弱.本文对气象各要素之间的灰色关联分析步骤如下:
1)为研究能见度要素与其他气象要素之间的关系,先对气象要素进行编号,记为Ai(i=1,2,3,4,…,11),并将各气象要素数据换算成标准单位制数值,Ai与各气象要素之间的对应关系如表1所示.
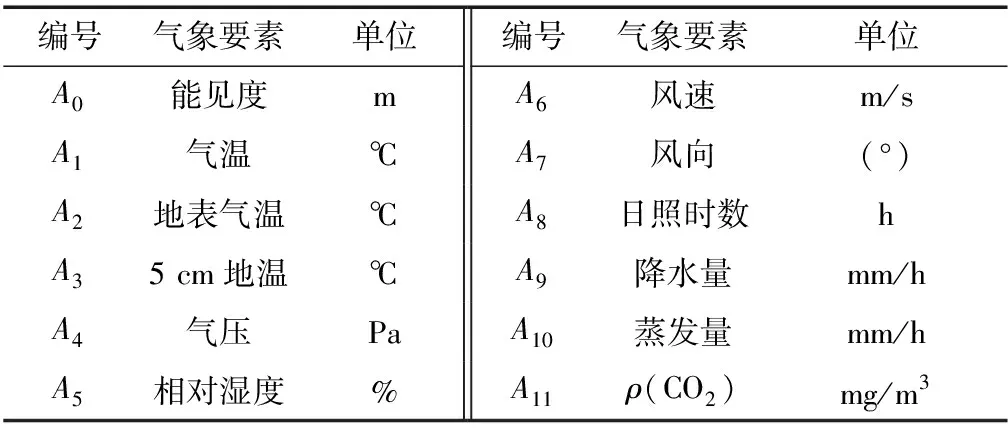
表1 各气象观测要素的编号序列
2)求表征关联度的关联系数.以能见度数据序列为参考数据,其他观测要素的数据序列作为比较数据.参考数列为A0={A0(1),…,A0(d),…,A0(N)},比较数列为Ai={Ai(1),…,Ai(d),…,Ai(N)},其中d代表各要素序列中的元素个数,N是选取数据序列的总数,1≤d≤N.
数据序列Ai与A0在第d点的关联系数εi(d)为
εi(d)=
(1)
式中:ρ∈(0,+∞) 称为分辨系数,通常在0到1之间选取,一般取ρ=0.5;i代表气象要素序号,1≤i≤11.
3)求各气象要素之间的关联度γ(A0,Ai):
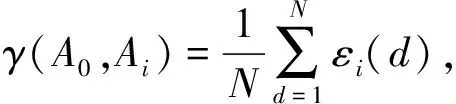
(2)
其中关联度γ∈(0,1),数值越大表明该气象要素与能见度的关联度越高.本文按照关联度数值从大到小的顺序选择输入要素,不妨设选择的输入要素为M个.
1.3 能见度数据预估模型
1.3.1 SVM能见度缺失值预估模型
SVM是把线性不可分的样本通过核函数映射到特征空间,进而在特征空间中构造最优分类平面,使样本到平面的总距离最小,由此实现拟合的[21].对于模型给定的训练数据总样本D={(xi(j),y(j)),i=1,2,…,M,j=1,2,…,N1},其中xi(j)为第i个气象输入要素的第j个样本,y(j)为对应的能见度实测值,N1为总样本容量.记x=[x1,x2,…,xM]T.首先利用一个非线性映射函数φ(x)将样本x从原空间RM映射到特征空间,然后在高维特征空间中构造最优决策函数:
y(x)=wT·φ(x)+b,
(3)
式中:φ(x)为映射函数;w为权向量;b为偏置量.权向量w与b通过优化下式得到:

(4)
其约束条件为
y(j)-wTφ(x(j))+b+ξ(j)=0,
(5)
式(4)中:C为惩罚因子,为给定值,其数值越大表示对训练误差大于设定误差的样本惩罚越大;ξ(j)为松弛变量,定义为ξ(j)=1-y(j),ξ(j)数值越大表示对样本训练误差的容忍程度越大.
在求解最小化问题(4)和(5)之前,首先要找到合适的非线性函数φ(x),为此引入径向基核函数:
j=1,2,…,N1,
(6)
并令K(x(β),x(j))=φT(x(β))·φ(x(j)),β=1,2,…,N1.进一步引入Lagrange方程,从而可以求解(4)和(5),得出SVM最优决策函数的估计函数为
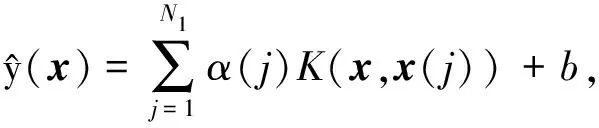
(7)
式中K(x,x(j))为核函数,拉格朗日乘子α(j)∈R,R为实数集.
本文根据以上原理,通过能见度与其他气象观测要素之间复杂的非线性关系进行能见度缺失值预估.具体步骤如下:
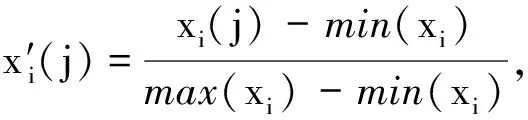
2)运用网络搜索法来分别对式(4)和式(6)中的C,δ两个参数寻优,其中惩罚因子C的搜寻范围在0.1~100,核参数δ的搜索范围在0.001~1,利用交叉验证法可获得最优参数[22].
3)利用建立的SVM能见度数据预估模型,对预处理后的样本数据进行训练,并对模型的预估结果进行评价.选用平均相对误差(MAPE,其量值记为ηMAPE)和均方根误差(RMSE,其量值记为ηRMSE)来评价:
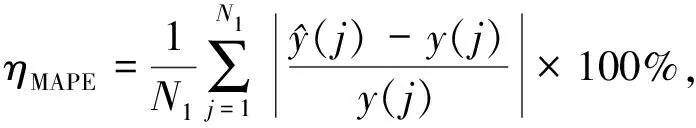
(8)
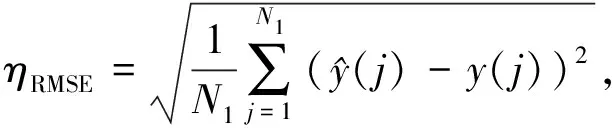
(9)
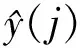
1.3.2 BP神经网络的能见度缺失值预估模型
BP神经网络能见度预估的基本结构如图3所示,其中输入层有m个节点,隐含层有p个节点,输出层有1个节点,Wig(i=1,2,…,m;g=1,2,…,p)为输入层到隐含层的权值,Wgk(g=1,2,…,p;k=1)为隐含层到输出层的权值,θg(g=1,2,…,p)为隐含层的阈值,σ1为输出层阈值,(X1,X2,…,Xm)为神经网络输入向量,Y1为神经网络输出量,Yh为期望输出,e为神经网络期望输出与实际输出的误差.
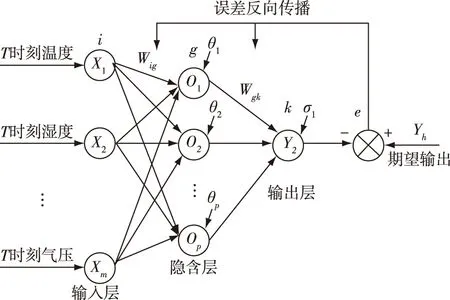
图3 BP神经网络能见度预估的结构Fig.3 Structure of BP neural network for visibility estimation
三层结构BP神经网络可用于预估气象站能见度缺失值,其中输入层对应与能见度相关性大的气象要素序列,输出层是能见度预估值.隐含层的神经元数量对模型预估结果的好坏产生直接的影响,但是目前没有能直接确认最优隐含层个数的方法,只有根据以下经验公式来计算:
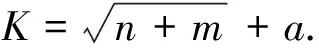
(10)
设定不同隐含层神经元个数,然后采用“试凑法”逐步增大和减少隐含层神经元数目使网络误差最小.式(10)中:m为输入层节点个数;n为输出层节点个数;a为常数,取值范围一般为3至10.K为隐含层神经元估算个数.
用于能见度缺失值预估的BP算法各步骤如下:
1)权值初始化:(wig∪wgk)=random(·),其中random(·)表示权值在[0,1]之间的均匀分布.
2) 依次输入训练集中的样本,设当前输入第q个样本.
3) 依次计算各层的输出:X′g,X″k及Y1.
4) 求各层的反传误差,并记下各个X″k(q),X′g(q),Xi(q)的值.
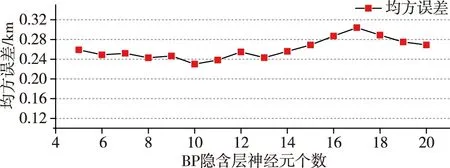
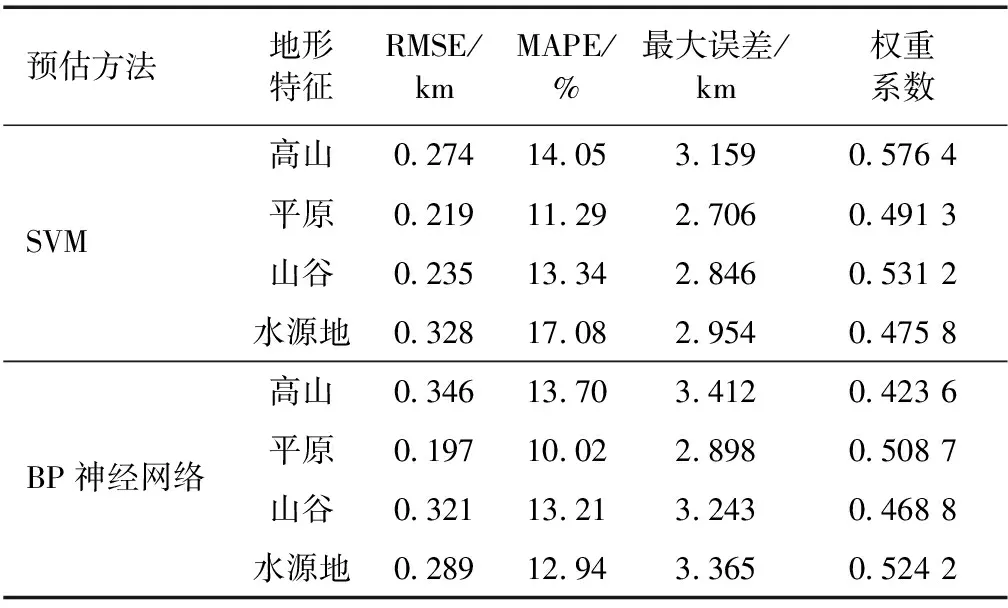
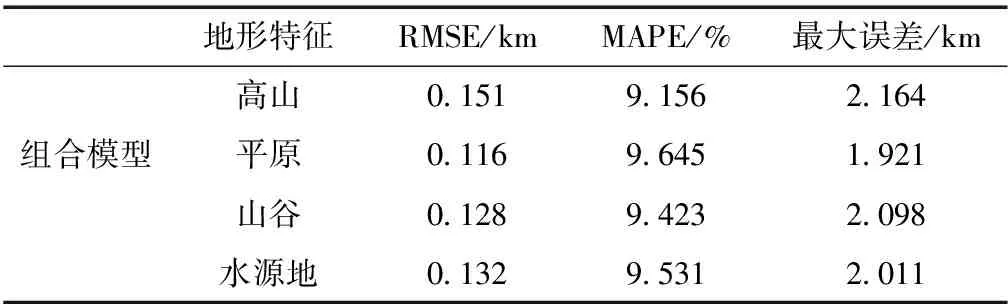
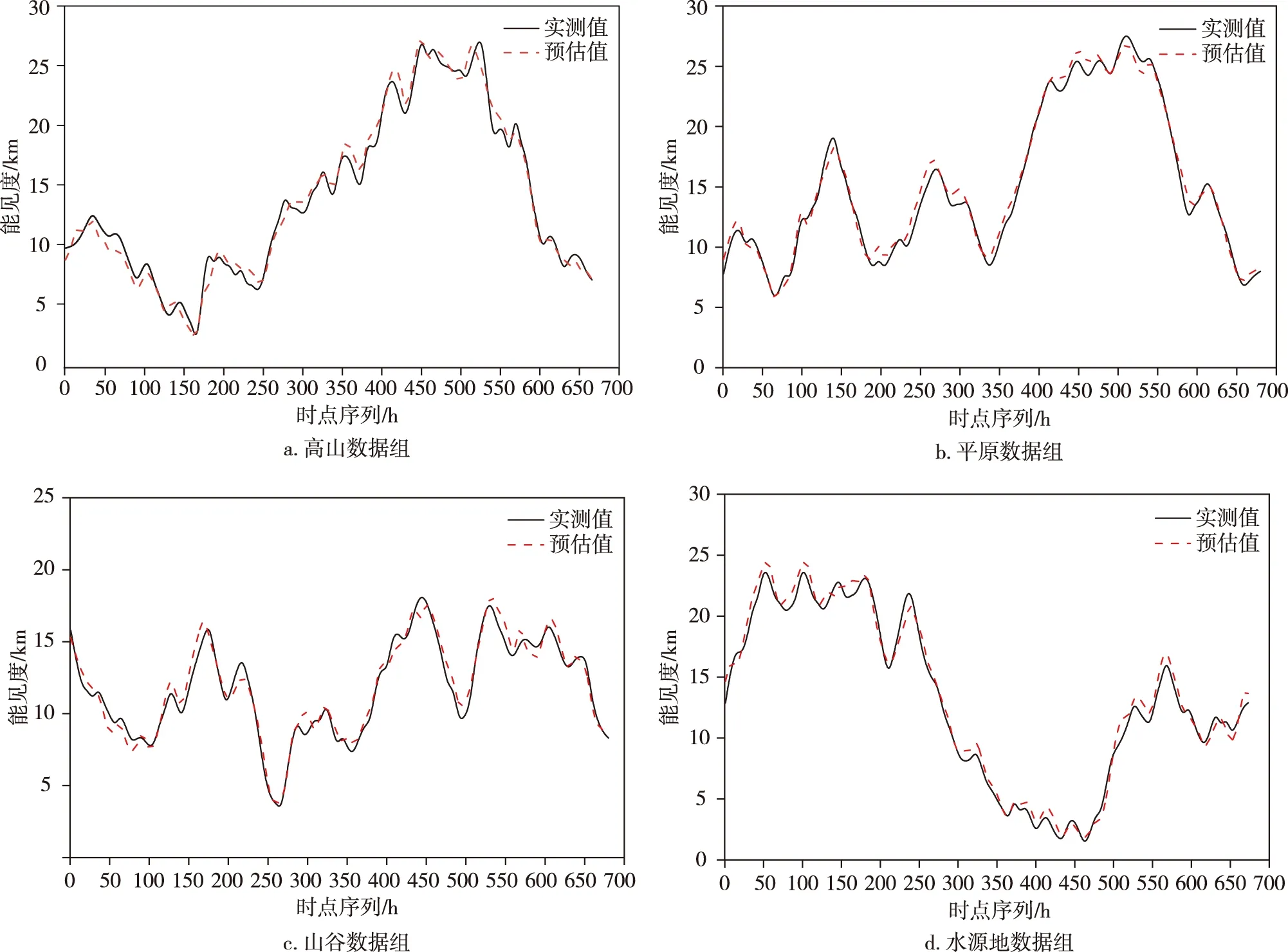
5)记录已学习过的样本个数q.如果q 6)按新的权值再计算X′g,X″k及Y1和学习样本数的总误差E,若E<ε(ε为预估给定误差),或达到最大学习次数,则终止学习.否则,转步骤2)继续新一轮学习. 1.3.3 组合模型 用不同的机器学习算法得出的能见度预估值与实测值都有误差.为了减小预估值与实测值之间的误差,可以整合不同模型的优点,对不同方法的预估结果进行加权组合,以提高预估精度.在组合模型预估中最关键的步骤是确定不同预估方法的权重.目前,针对多模型组合权重确定,常用的方法主要有以下几种:算术平均法、方差倒数法、均方倒数法以及最小二乘法.本文采用方差倒数法判断单项模型系数,即对误差平方和小的模型赋予较高的权重,误差平方和大的赋予较小的权重,使组合模型的误差和尽可能小.具体方法如下: 设F为观测对象,其实际观测值向量为(F1,F2,…,Fn),U1,U2,…,Ur为r种不同预估方法得出的预估值,向量S=(S1,S2,…,Sr)T中元素分别是它们在组合模型中的权重,第l个预估方法Ul的预估值为(U1l,U2l,…,Unl).则组合模型的估计值为 (11) 其中 (12) 一般关联度大于等于0.8时,子序列与母序列关联度很好.根据1.2节的理论,可以计算得到其他观测要素与能见度之间的关联度,本次实验选择与能见度的关联度在0.8以上的气象观测要素,如表2所示. 表2 部分气象要素与能见度之间的关联度 本文采用的SVM模型预估能见度实验,借助的是Pycharm软件的libsvm工具箱,其实验精度主要取决于参数选取是否合适,本文各参数设定值如表3所示. 表3 SVM最优参数值设置 在BP预估实验中,BP神经网络模型以与能见度要素关联度高的8个气象要素作为输入,隐含层选用单层结构,依据估算最优隐含层神经元个数的经验公式,推算出K值在[6,13]之间.为了保证隐含层神经元个数对模型预估结果的准确性,设定隐含层神经元个数K在[5,20]区间.将平原组训练集归一化处理后输入BP模型中,取不同隐含层神经元个数,用一组验证集记录相对误差均值.由于初始权值随机分配,相同个数的隐含层神经元运行的结果也有不同,所以BP网络中每个K值的设定都运行10次,误差结果算平均值,寻优过程如图4所示. 图4 隐含层神经元个数寻优Fig.4 Optimization of the number of neurons in hidden layer 由隐含层神经元寻优结果可知,BP神经网络预估模型选用10个隐含层神经元最佳.其中BP神经网络的训练最大迭代次数设定为50 000次,学习率取0.1,迭代循环次数上限值取20,训练最终误差设定为0.001,激活函数选择双曲正切函数,训练函数及学习函数均采用Levenberg-Marquardt算法. 对不同地形代表站的测试集数据分别采用已训练好的SVM和BP模型进行预估,测试集预估结果和实测结果进行对比分析,求出各地形预估值与实测值的误差平方和,运用方差倒数法,得各自的权重系数如表4所示. 表4 两种方法单一预估结果 将两种方法的训练集预估结果进行对比分析,由表4可知,在这四种地形中,SVM缺失值预估模型要比BP神经网络的更加稳定,误差也更小,但是在水源地和平原地形中BP神经网络的预估结果准确度相对更高,结合两种模型预估的结果,可以提高能见度预估的精度.实验输入测试集数据得到两种模型的预估结果,运用上文所述的方差倒数法,加权组合求出组合模型的预估值,并计算组合模型预估值和实测值的平均相对误差、误差均值和最大误差.测试集能见度组合模型预估性能指标结果如表5所示,预估效果如图5所示. 表5 组合方法的性能参数对比 图5 各地形能见度数据组预估效果Fig.5 Comparison of observed visibility and estimation by the combined SVM-BP neural network method for mountainous (a),plain (b),valley (c),and water source (d) areas 从表5中的实验结果数据可以看出,无论是哪种地形,组合模型预估的平均相对误差更低,整体误差均值小,效果要明显好于单一模型.由此可知,组合方法可以保留单一模型的预估优势,增加对缺失数据预估的可靠性. 为解决自动气象站能见度要素缺测的问题,本文利用组合模型对缺测数据进行精确的预估,并以预估值代替实测值来保证数据的完备性.首先通过灰色关联分析方法精简预估模型输入,筛选出与能见度相关度较大的气象要素,再从气象信息的多种要素中建立能见度数据预估模型.在实验部分,两种模型对能见度都具有良好的预估能力,SVM模型在四种地形中对能见度数据的预估结果比较好且稳定,而BP神经网络则对平原和水源地的数据预估能力突出.对不同模型预估的结果加权组合,结合测试集的RMSE和MAPE的数据,将这些数据与单一预估的方法对比,结果表明组合模型预估的方法更加接近实测值,更能充分地利用数据信息,从而提高对缺失数据预估的准确性.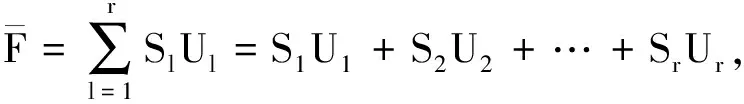
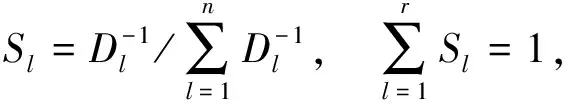
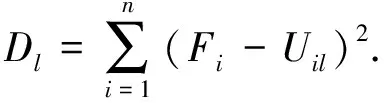
2 实验与分析
2.1 能见度影响因子的选择
2.2 SVM与BP方法组合模型预估

2.3 组合模型预估实验结果
3 结论
