旋转纸牌轨迹的近似理论计算

朱世栋，黎秋航，侯吉旋，陈 乾

(1.东南大学 物理学院，江苏 南京211189；2.东南大学 交通学院，江苏 南京 211189)

在2020年国际青年物理学家锦标赛(IYPT2020)的第17题中描述了一个生活现象，题目的中文翻译如下：“一张标准的扑克牌只要在投掷的过程中旋转，就可以运动很长的一段距离.研究影响距离和轨迹的参数”.定性来看，纸牌旋转后飞行会更加稳定，可以保证薄边始终正对运动方向，迎风面积的减小会导致正面空气阻力的减小，而下表面受到向上的空气阻力会导致下落时间的延长，两相叠加，致使运动距离的增大.其中，旋转纸牌飞行的稳定性可以用刚体的欧拉公式来解释[1].

要分析纸牌的轨迹，就无法避免对纸牌表面气体流动的研究.对于一般意义的平板绕流问题，已经有众多学者进行了理论研究和数值模拟，姜海波等人[2]更是为大攻角的气体绕流问题提供了解决方案，以适应低速情况.然而，对于旋转中的纸牌，其周围的气体流动比平动情况要复杂得多.目前对于旋转刚体在空气中运动的研究还很少，王一坤等人[3]运用空气动力学分析了竹蜻蜓的飞行过程，田爱平等人[4]更是发现了竹蜻蜓飞行过程的进动现象.然而，竹蜻蜓的转动与纸牌的转动有着本质的区别，竹蜻蜓通过两个交错的桨叶产生升力，而纸牌表面各点始终在一个平面.本文试通过建立简单的纸牌模型，对旋转纸牌的运动进行探究.

1 理论模型

设纸牌为刚体，不会发生弯折等形变.再设纸牌的本征坐标系为Cxyz，地面坐标系为OXYZ，如图1所示.设纸牌质量为m，长为a，宽为b，厚度为h，空气密度为ρ，空气阻力系数为k，黏度为η，纸牌的初速度为v0、角速度为ω0，运动过程中纸牌转角为θ.纸牌受力包括：重力；下表面空气阻力(升力)；上下表面黏滞阻力；马格努斯力；边缘空气阻力.这里已忽略纸牌边缘的黏滞阻力.本节将定量求解出各力大小，以便轨迹的计算.

图1 纸牌模型图

1.1 上下表面黏滞阻力

设黏滞阻力与相对速度的一次方成正比[5]，则任意面元的黏滞阻力可按照速度方向进行分解.面元的速度由质心速度与相对质心的旋转速度构成，不妨将黏滞阻力沿这两个方向进行分解.

如图2所示，Ffv为与质心平动速度有关的黏滞力，宏观不产生力矩；Ffω与绕质心转动速度有关的黏滞力，宏观只产生力矩；r为面元P到质心C的距离.

图2 黏滞阻力分析图

黏滞力与力矩通过简单积分可得：

(1)

1.2 马格努斯力

马格努斯力是由纸牌边缘气体流动导致的压力差所形成.忽略纸牌边缘的黏滞阻力，可近似满足“定常流、无摩擦流、不可压缩流”条件，故可近似使用伯努利方程.

如图3所示，P1面元在Cxyz坐标系中的坐标为(b/2，y)，P2坐标为(-b/2，-y)，P3为(b/2，-y)，P4为(-b/2，y).P1与P2关于原点对称，与P3关于x轴对称，与P4关于y轴对称.设质心沿X方向的速度大小为vX，沿Y方向的速度大小为vY.P1、P2、P3、P4的速度均由质心速度与绕质心旋转的速度合成而来，其分速度都标于图3中.

图3 侧面元速度分析图

对侧面元P1、P2，其平行于侧边的速度为：

(2)

由伯努利方程可得沿x方向的压强差：

(3)

对长边积分可得x方向的马格努斯力：

Fx=-ρωabh(vXsinθ+vYcosθ)

(4)

同理对短边计算压力差，可得y方向的马格努斯力：

Fy=ρωabh(vXcosθ-vYsinθ)

(5)

合成到X、Y方向：

(6)

很容易发现任意关于x轴对称的面元(如P1、P3)受到的压力相等，因此马格努斯力不产生力矩.

1.3 边缘空气阻力

先研究长边上的空气阻力.只有当侧面元有沿外法线方向的速度时，才能产生空气阻力.

如图3所示，不难发现，关于y轴对称的侧面元(如P1、P4)垂直边缘的速度相同.当y>0，x>0时，侧面元速度沿外法向，有阻力；当y>0，x<0时，侧面元速度沿内法向，无阻力.但是，y<0的情况较复杂，面元速度方向不仅取决于y坐标，还与vX、vY、ω、θ有关.为避免复杂的分类讨论，我们取长时间的平均(即忽略旋转)：

(7)

这里假设了空气阻力与迎风速度的二次方成正比(实为平板绕流的结论)[6].而阻力矩为周期性变化，平均后为0.

2 进动现象

2.1 纸牌进动及其原因

在尝试不同初始条件进行实验的过程中，可以发现，当纸牌运动时间较长时，会发生明显的竖起，且纸牌薄边能始终正对运动方向.设角动量为L，由现象知，L会在垂直于速度方向的平面内转动，即纸牌在进动.此进动对纸牌轨迹有重要影响.

为探求纸牌进动的原因，需要寻找合适的力矩.在纸牌水平时寻找，由于纸牌上下的对称性，显然没有合适力矩能够使其发生进动.因此可假设，纸牌在空中受到微扰产生初始进动角速度，此角速度会产生力矩促生进一步的进动.

经过不断的尝试，可排除：边缘空气阻力(无法产生力矩)；马格努斯力(无法产生力矩)；上下表面粘滞阻力(上下对称性使合力矩为0).唯一可能产生有效力矩的是只有下表面存在的空气阻力.如图4所示，建立CX’Y’Z’坐标系，其中X’轴指向水平速度方向，则进动应发生在CY’Z’平面内.设进动角速度为Ω=(-Ω0 0)(在CX’Y’Z’坐标系下)，进动角为φ.下面进行定量计算.

图4 纸牌进动的原因

已知本征坐标系Cxyz与运动坐标系CX’Y’Z’的转换关系：

(8)

(9)

其中i、j、k为Cxyz坐标系的单位矢量，i’、j’、k’为CX’Y’Z’坐标系的单位矢量.因此，对于坐标为(x，y，z)的面元，转换到CX’Y’Z’坐标系后的坐标为

(X′Y′Z′)=(xyz)

(10)

进而可得CX’Y’Z’坐标系下面元的进动速度：

(11)

换回Cxyz坐标系：

(12)

只取z分量，代入化简得

vΩ⊥=Ω(xsinθ-ycosθ)

(13)

故面元垂直表面的合速度为

v⊥=-vZ′cosφ+Ω(xsinθ-ycosθ)

(14)

此处已利用vY′≡0的运动坐标系特征.而此微元受到的空气阻力为

(15)

空气阻力对质心的力矩为

=(ydFf-xdFf0)

(16)

此力矩换到CX’Y’Z’坐标系：

dM′=(ydFf-xdFf0)

(17)

由式(15)(17)，对纸牌平面积分即得总力矩：

(18)

对式(18)进行分析.MX’不为0，说明纸牌应有X’方向的进动，但现象中进动只发生在CY’Z’平面，这可以用欧拉方程解出的旋转稳定性解释[1].

因此，我们忽略了X’方向的进动，将重点放在Y’,Z’方向上.会发现一个十分漂亮的结果.令

则由式(18)得

(19)

发现产生进动的合力矩恰好与角动量方向垂直，如图5所示.正是这力矩使角动量L在CY’Z’平面内转动.

图5 合力矩方向与角动量方向

2.2 运动方程

此进动对纸牌轨迹的影响显著.定性来看，一方面，由于纸牌的立起，沿Z’方向的阻力分量减少，导致飞行时间的缩短.另一方面，由于纸牌的立起，沿X’负方向、Y’方向的阻力分量增加，导致纸牌发生明显的侧飞.定量来看，需要求解纸牌的运动方程.

首先利用角动量定理求解进动角.

(20)

不难发现，式(20)解出的是一个与Ω无关的恒等式，通过此等式可以发现一些有趣的规律，但与本文研究无关暂不予讨论.等式与Ω无关，可视为初始进动角速度Ω0确定后，产生的力矩将与Ω保持平衡，不会再使其发生改变.即

Ω=Ω0

(21)

知晓了纸牌的进动规律，就可以求解下表面空气阻力在3个方向的分量，从而求解运动方程.由(15)式积分，再转换到OXYZ坐标得

(22)

其中

此处已利用vZ’=vZ.比较各力大小：忽略a、b等共有项，黏滞阻力中含有黏度η，为10-5数量级[7]，马格努斯力与边缘阻力均含有纸牌厚度项h，均为10-4数量级.因此，相比下表面空气阻力，其它力对纸牌运动的影响微乎其微，可以忽略.于是动力学方程为

(23)

结合式(22)即可求解出X(t)、Y(t)、Z(t).

2.3 参数分析

式(23)表示的动力学方程较复杂，因此无法求出运动方程的解析解，但可以通过数值解进行参数分析，得出纸牌运动的一些规律.不同参数下X(t)、Y(t)、Z(t)的数值解如图6所示.

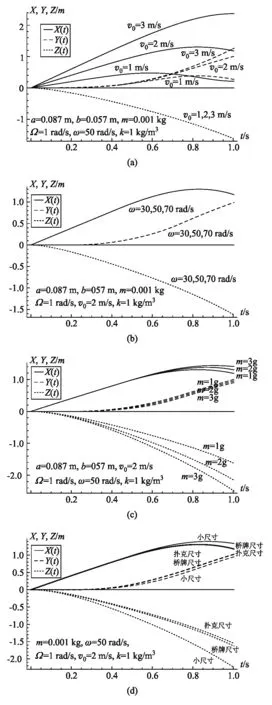
图6 可能参数下的运动轨迹

其中，图6中的(a)图为初速度大小v0不同时的情况.可以发现，v0较小时，不仅X方向的运动较慢，Y方向速度也较小，甚至会出现回旋的情况，而初速度大小对Z方向的运动没有影响.(b)图为角速度大小ω不同时的情况，不难发现，只要ω足够大，足以保持纸牌旋转稳定，则ω的变化对运动没有影响.(c)图为纸牌质量m变化时的情况，可以发现，m越大，X方向运动占比越多，Z方向下落得越快，即纸牌受到气流的影响越小，这与常识相符.图(d)为纸牌尺寸不同时的情况，其中小尺寸Mini Size(3.7 cm×6.0 cm)、桥牌尺寸Bridge Size(5.7 cm×8.7 cm)、扑克尺寸Poker Size(6.3 cm×8.8 cm)为市面常见的尺寸，可以发现，尺寸越小，X方向运动占比越多，Z方向下落越快，即纸牌受空气影响越小，这与常识相符.

实际上，进动角速度大小Ω也是影响运动的重要因素，但它是ω、v0等多变量的函数，具体关系需要对绕流情况更精确的建模.本文将其认为是不变的常量，其值可以由实验测得.

3 实验验证

本节设计了实验对真实纸牌轨迹进行了分析，并在一定程度上验证了前文的运动规律.手动扔纸牌无法对其初速度、初角速度等进行控制，因此本文自主设计了一个纸牌发射器，如图7所示.

图7 纸牌发射器示意图

此发射器以两个可正反双向转的飞轮为主体，两边各六档可调.其中，A为档位调节器，用于控制飞轮转向和转速，B为发动机，C为飞轮，用于传动的，D为齿轮，E是放置纸牌的平台，F是可活动支撑轴，通过改变飞轮与平台的距离，可以控制飞轮给予纸牌的压力.此装置的优点：1)相同条件的可重复性.通过在相同档位发射纸牌，可以很大程度上保证纸牌出射状态相同；2)纸牌水平出射.两个飞轮的对称设计可以保证纸牌不会因一边受压而翘起，从而保证水平出射；3)初速度与初角速度不会产生一一对应关系，方便后续的控制变量研究.

通过物理影像分析软件Tracker，可以测出纸牌发射的初速度、初角速度与进动角速度.利用侧视与俯视的拍摄，可以拟合出X、Y、Z方向的轨迹方程.通过选取多组条件进行实验，并与理论进行了对比.选出有代表性的一组如图8所示.

其中阻力系数k是通过静止释放纸牌测量落地时间得到的.可以发现，实验与理论的契合程度较高.但尝试过多组条件后，可以发现实验中X方向的运动占比均比理论要高，下落速度也均比理论要快，即空气的影响并没有预想中的那么大.这一方面可能来源于物理影像分析软件Tracker视差等实验误差，另一方面可能是我们的模型还可以进一步完善.

X、Y、Z轴方向上运动轨迹的理论与实验对比

4 总结与讨论

本文在假设纸牌稳定旋转的前提下，利用平板绕流和刚体动力学规律，近似计算了一个纸牌的运动轨迹，并通过参数分析得到了纸牌运动的一些规律.可以发现，影响纸牌运动的主要力是下表面的空气阻力，它一方面导致了纸牌的进动，一方面通过进动产生了3个方向的分力.本文进而利用自主设计的纸牌发射器，在一定程度上验证了理论，具有较高契合度.事实上，旋转纸牌周围的空气流动比平动情况的平板绕流要复杂，进动过程也不能简单地用空气阻力来解释.更完善的模型需要更深刻的空气动力学理论进行指导，这有赖于后续研究.