大学物理设计实验：李萨如图形演示装置研究

吴 晗,于 瑶,游胤涛,唐永军,张锦龙

(1.上海科技大学 物质科学与技术学院，上海 201210；2.同济大学 物理科学与工程学院，上海 200092)

综合设计性物理实验与基础大学物理实验不同，它没有内容详尽的标准教材，只给出设计题目和要求，充分发挥学生的主观能动性和科学探索精神，从查阅资料，确定实验方案，配置实验仪器，购买实验耗材，到进行实验，分析数据，撰写实验论文报告，模拟了科学实验的全过程.设计性实验常具有一定的探索性、研究性、创新性、综合性，有利于培养学生的创新能力和提高学生的科学素养，同时也促进实验教师专业水平的提高，因此在大学开设设计性物理实验是十分必要的[1-2].

实验室自制李萨如图形演示装置，因其实验装置灵活多变，现象有趣直观，实验原理涉及力学、光学、声学、电学等多个学科，完美地将趣味性、创新性和研究性结合在一起，非常适合作为大学物理中的综合设计性实验[3-8].目前基于薄膜的受迫振动形成李萨如图形的研究，有的只建立了理想的薄膜振动理论模型，忽略了复杂的实际振动情况，并没有给出对应的实验结果[9].有的仅设计了一种李萨如图形产生装置，根据产生的李萨如图形估算气球薄膜本身的固有频率，没有详细正确的理论分析[10].

本文基于以上研究，自制了一种更加简易的李萨如图形演示装置，得到李萨如图形大小和形状随着驱动声源频率的变化规律，并结合柔性薄膜受迫振动的理论对实验现象进行分析，然后根据实验中测得的薄膜振动的共振频率值，计算出常见的乳胶气球薄膜面积扩大到一倍时的表面张力值，表明该实验装置具有一定的实际应用价值.

1 实验器材与装置

李萨如图形演示实验装置所需材料如图1所示，主要包括：1为智能手机，手机上下载Sound Generator APP软件，用来产生不同频率的声源信息.2为常见的塑料圆筒.圆筒的底部用剪刀剪掉，开口端用橡皮筋固定常见的乳胶气球，形成一层柔性气球薄膜.3为其拉伸后面积约为松弛状态的两倍.这里圆筒作为共振腔，使声波得到加强.4是1 cm×1 cm的平面镜，质量为0.52 g，用双面胶将平面镜固定在薄膜的中心位置，主要作用是将照射过来的激光反射到接收屏上.5是波长为650±10 nm的红色激光笔，功率约为5 mw，作为光源照射到平面镜上.图形接收屏为表面平整的黑板.该实验装置耗材成本低，并且构造简易，便于学生动手制作，极大地激发了学生的探索与学习兴趣，在大学物理综合设计实验教学中有很好的推广性和适用性.

图1 自制李萨如图形演示装置

2 理论模型分析

本小节忽略了空气媒介影响，介绍薄膜在声源作用下受迫振动的理论基础[11]，并分析李萨如图形的形成原因.

由于气球薄膜富于弹性，且容易变形，可将其视为一种柔性膜，忽略其劲度的影响.所以当薄膜受到外力扰动后，恢复到平衡位置的主要是张力T.膜上的张力可以通过该点所绘出的线元长度两边的拉力表示，单位为N/m，是个矢量，可以垂直也可以不垂直这个线元.如果薄膜是完全柔性的，张力在整个面积上均匀分布，方向垂直于线元且大小相同.

因实验装置中的薄膜是圆形膜，这里选择在极坐标系下求解，图2表示的是极坐标系下作用于面积元上的力.

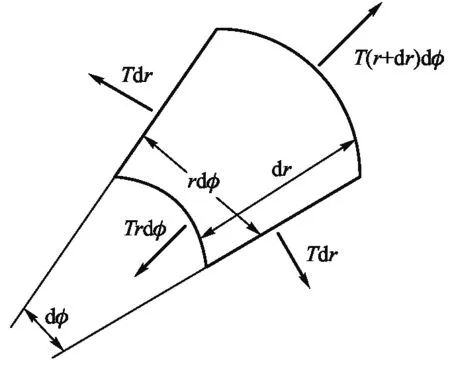
图2 极坐标系下作用于薄膜元面积的力

脱离平衡位置的横向位移用η表示，在极坐标系下η是径矢r、极角φ和时间t的函数，波动方程的形式为

(1)

当薄膜的表面受到均匀的声波作用时，声压P=PAexp(iωt)，这里PA为声压的振幅，单位为N/m2，ω为声源的频率，由于这一外力的存在，式(1)可改写成式(2)的形式，即薄膜的受迫振动方程为

(2)

假设振动还是简谐方式，其试探解η(r,φ,t)=ηa(r,φ)eiωt，求解可得

ηa(r,φ)=AmJm(kr)cos(mφ-φm)

(3)

这里Jm(kr)为m阶的柱贝塞尔函数，m=1,2,3,…，圆对称模型是m=0时的特例.φm为初相位，与实验装置初始条件有关.

根据边界条件可知非对称振动的简正频率满足式：

Jm(ka)=0

(4)

式(4)为一般圆膜振动的频率方程，显然对应不同的m值，有不同的柱贝塞尔函数根值，以此得到不同的简正频率值fmn：

(5)

表1列出了m阶柱贝塞尔函数的一些根值.

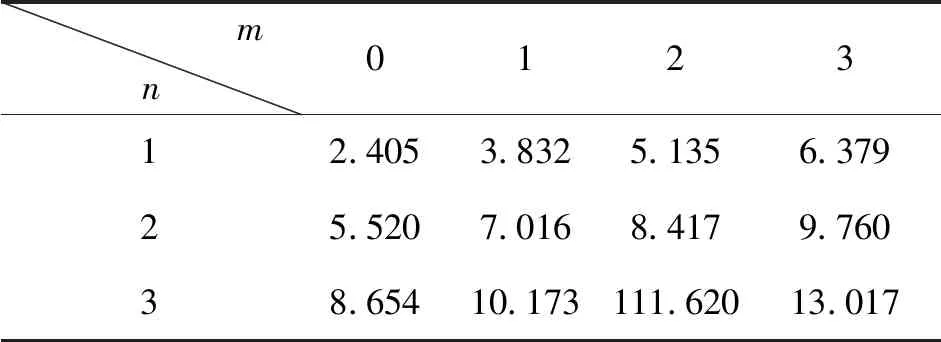
表1 Jm(μ)=0的根值μmn

如果只考虑薄膜表面是圆对称时，即不考虑φ值的影响，当薄膜进行受迫振动时，它的位移振幅与径向位置和声源频率有关，对其取位置的平均，

(6)

以上为薄膜的横向振动模式，当薄膜的横向位移大到足以使张力大小发生实质性变化时，面积元左右两侧的受力不相等，合力将使面积元产生偏离平衡位置的径向位移，这时候不仅要考虑膜的横向运动，还要考虑其纵向运动，这就是合成李萨如图形的第二个分振动. 已知一维柔性弦的纵向振动是由横向振动引起的，二者相互耦合，而纵向振动的频率一般为横向振动的整数倍[12]. 对于薄膜来说，增加一维会引进一些额外的现象，其纵向振动的理论分析则更加复杂，这里不再过多阐述.

3 实验结果分析

在实验过程中，首先固定激光笔到平面镜的距离，使激光入射到平面镜上.然后将手机放置于圆筒里，扬声器开至最大，打开Sound Generator APP软件，选择正弦波形，缓慢调节软件输出声源的频率范围，并观察接收平板上形成的李萨如图形，结合理论分析图形形状、大小和相位随频率的变化规律，找到某一特定初始条件下，薄膜实际振动的共振频率，并计算气球薄膜面积扩大一倍时的表面张力值.

3.1 第一周期的实验现象

图3为频率从90 Hz到150 Hz对应的图形变化，左上角数字表示图形对应的声源频率，需要说明的是当频率从20 Hz到90 Hz时，接收屏上都显示圆点状.图形的变化规律如下.

图3 声源频率为90 Hz～150 Hz的图形变化

频率从90 Hz过渡到95 Hz时，开始有右旋方向的短线出现，短线随频率逐渐变长，根据李萨如图形，可判断此时两个垂直振动的频率比为1，相位差为0.当频率为96.5 Hz和99 Hz时，出现频率为2∶3的李萨如图形，二者的相位差为π.从实验结果来看，二维薄膜纵向振动频率与声波驱动频率比值存在2∶3的情况，表明其纵向振动频率与外力驱动频率有关，从实验上证实了薄膜纵向振动模式是由横向振动产生的.

当声源频率为101 Hz时有椭圆形状出现，然后椭圆形状更加明显，即相位差增大.频率为107 Hz时相位差达到最大；频率为110 Hz时，椭圆形状达到最大，表示振动振幅达到最大，该频率为薄膜受迫振动的第一共振频率，理论上等于第一简正频率.薄膜振动的简正频率公式fmn=μmnc/(2πa)，当m=0,n=1时，由表1可知μ01=2.405. 图1实验装置中，游标卡尺测得薄膜的直径为86.58 mm，电子秤测得气球薄膜的质量为1.53 g，圆心镜片质量为0.52 g.根据简正频率公式和系统等效质量公式可以计算出薄膜的等效表面张力T1=44.78 N/m.

随后图形的振幅和相位差又随着频率变小，当频率为114 Hz时，再次成为相位差为0的直线形状，直线形状逐渐变短.当频率到135 Hz时，短线由右旋转变为左旋形状，左旋图形同样随着频率由直线到椭圆(148 Hz)，再到直线(150 Hz)，即相位差从π降低到一定值，又增加到π.频率为155 Hz时图形再次成为点状.

3.2 其他周期的实验现象

第二周期的李萨如图形变化如图4所示，该周期的横纵振动频率比都为1.从155 Hz的点状结构开始，160 Hz时形成右旋长线，然后相位差逐渐增大，175 Hz时椭圆相位差达到最大.然后相位差开始减小，直到185 Hz附近，相位差逐渐减小为0.在频率185 Hz到195 Hz之间还是存在短线过渡，与第一周期的变化类似，195 Hz时出现相位差为π的左旋直线.接着相位差由π逐渐减小至最小值，到215 Hz时相位差又增加到π，图形成为直线形状.220 Hz时，图形再次成为点状结构，至此第二周期的图形变化结束，对应的频率间隔也为65 Hz.需要指出的是，当频率为180 Hz时，图形形状达到最大，理论分析应该为薄膜受迫振动的第二共振频率，这时对应的μ11=3.832.同理根据简正频率公式计算得出表面张力T2=47.23 N/m，与T1数值稍有差别，原因可能是本文使用的理论模型是假设薄膜在真空中振动，没有考虑实际的传播媒质空气、腔体对振动的影响，并且实际的薄膜和圆心平面镜的等效质量不一定严格类似弹簧振子等效质量的表达式，所以两次计算的数值有稍许偏差.平均两次计算结果，可得出气球薄膜面积扩大一倍时的等效表面张力T=46.00 N/m.

图4 声源频率为155 Hz～220 Hz的图形变化

图形到220 Hz成为点状，并且点状结构一直持续到240 Hz左右，然后开始第三周期的图形变化，根据公式6和表面张力值，可知薄膜的反共振频率公式fan=μ2nc/(2πa)，当μ21=5.136，计算出fa1=μ21c/(2πa)=238 Hz，是与实验情况基本相符合的.

第三周期的图形随频率的变化趋势与前两个周期类似，横纵振动的频率比都为1，但是整体图形的形状随着频率增加而变小的趋势，与贝塞尔函数图形变化相似，这里不再叙述.

3.3 进一步分析与讨论

在实际的实验教学过程中，不同同学制作的实验装置有一定的差异，就使得薄膜振动的初始条件不同，就会得到不同的图形变化规律，但是都可以根据实验中的共振频率值计算各自实验装置中薄膜的表面张力值.

富于探索精神的同学在原始装置的基础上，可以稍微改变一些初始条件，比如将单声源换成多个声源，将气球薄膜替换成其他材质薄膜，或者是减小薄膜半径等，这都为学生提供了更多、更深层次的研究方向.例如图5(a)是频率为216 Hz和316 Hz叠加得到的图形，它是一种轨迹稠密地分布在矩形面内的准周期运动[13].准周期运动在结构上是不稳定的，稍有参量的变化，两个振动的频率会锁定到一个相近的有理数比值上，如图5(b)所示，只是将其中的216 Hz降低到210 Hz，就可以得到频率比为有理数2∶3的李萨如图形.因多个声源引起的薄膜横纵振动之间的耦合更加复杂，还有待于研究.

图5 两个频率声源叠加的图形

4 结论

本文理论分析了气球柔性薄膜通过受迫振动形成李萨如图形的原因，并自制实验装置得到相应的实验结果，然后根据实验中测得的共振频率值，估算出乳胶气球薄膜面积增大一倍时的等效表面张力值约为46.00 N/m，由此可见该简易实验装置的实际应用性和巧妙性.

该实验装置虽然简易，但运用的理论知识涉及到力学、光学、理论声学等多个方面，学生从理论中分析实验结果以及可能存在的误差来源，理论和实验相互改进和完善，而不是漫无目的进行多次实验，到最后提交小论文作为研究成果，整个过程非常锻炼学生实验数据分析处理能力和理论探究思考能力，为学生进一步的科研工作打下基础.相比于传统的大学物理实验，该设计性实验将创新性、趣味性和理论探究性结合到一起，明显更受学生的欢迎和认可，起到了非常好的教学效果.