Thermodynamics and phase transition of topological dS black holes with a nonlinear source
2021-10-13HuiHuaZhaoLiChunZhangandFangLiu
Hui-Hua Zhao,Li-Chun Zhang and Fang Liu
1 Institute of Theoretical Physics,Shanxi Datong University,Datong 037009,China
2 Department of Physics,Shanxi Datong University,Datong 037009,China
Abstract We discuss black hole solutions of Einstein-Λ gravity in the presence of nonlinear electrodynamics in dS spacetime.Considering the correlation of the thermodynamic quantities respectively corresponding to the black hole horizon and cosmological horizon of dS spacetime and taking the region between the two horizons as a thermodynamic system,we derive effective thermodynamic quantities of the system according to the first law of thermodynamics,and investigate the thermodynamic properties of the system under the influence of nonlinearity parameter α.It is shown that nonlinearity parameter α influences the position of the black hole horizon and the critical state of the system,and along with electric charge has an effect on the phase structure of the system,which is obvious,especially as the effective temperature is below the critical temperature.The critical phase transition is proved to be second-order equilibrium phase transition by using the Gibbs free energy criterion and Ehrenfest equations.
Keywords: dS black holes,nonlinear source,effective thermodynamic quantities,phase transition
1.Introduction
Since the four laws of black hole mechanics were discovered,black holes have been widely believed to be thermodynamic and they possess standard thermodynamic quantities,such as temperature and entropy [1,2].The particular thermodynamic quantities of a black hole and its holographic properties are quantum essentially,so a black hole is a macroscopical quantum system.The studies of black hole thermodynamic properties provide an important window to investigate quantum gravity [1–3].Phase transitions and critical properties are important and interesting subjects when studying a thermodynamic system,and recently,the critical behavior and phase transitions of black holes in antide Sitter(AdS)spacetime have been extensively investigated.By considering the cosmological constant as thermodynamic pressure,charged black holes show similar phase transitions to that of van der Waals–Maxwell’s liquid-gas.[4–25].Researchers have also been trying to discover a series of common thermodynamic systems to simulate the phase transition and critical properties of black holes [26–29].
In the early period of inflation,the Universe is in quasi de Sitter (dS) space.The cosmological constant corresponding to vacuum energy is usually considered as a candidate for dark energy,with which our Universe will evolve into another dS phase.In order to construct the entire evolution history of our universe,we should have a clear perspective of the classical and quantum properties of dS space.Promoted by the recent success of AdS/CFT correspondence in theoretical physics,the duality relation of dS space has also aroused interest[30,31].Therefore,from an observational or theoretical point of view,it is rewarding to have a better understanding of the classical and quantum properties of dS space.
As the thermodynamic properties of AdS black holes are investigated in depth,the study of the physical properties of dS black holes has gradually aroused great interest [32–37],and more attention has also been paid to the phase transitions and critical behavior of dS black holes [38–47].It is known that with the appropriate parameters dS space possesses not only a black hole event horizon (BEH) but a cosmological event horizon (CEH).Moreover,the two horizons generally have different radiation temperatures.Considering the two horizons as two thermodynamic systems that respectively correspond to two sets of thermodynamic quantities,both satisfy the first law of thermodynamics [48,49].Taking into account the thermodynamic relevance of the two horizons of dS black holes and considering the region between the two horizons as a thermodynamic system in non-thermal equilibrium [42–45,50,51],the thermodynamic behavior of some dS black holes is discussed by utilizing effective thermodynamic quantities.
As advances in related fields steadily grow,we start to gain a better understanding of the nature of black holes.In this work,we want to generalize the phase transition study to dS black hole solutions in Einstein gravity coupled to a nonlinear electromagnetic field.Nonlinear electrodynamics (NLED) theories are considerably richer than Maxwell field and in a special case they reduce to the linear Maxwell theory.About eighty years ago,Born and Infeld introduced an interesting kind of NLED in order to remove the divergence of the self-energy of a point-like charge[52].Recently,it was shown that NLED objects can remove both the big bang and black hole singularities [53–58].The first attempt to couple the NLED with gravity was made by Hoffmann[59].Since then,the effect of Born–Infeld(BI)-type NLED coupled to the gravitational field has been extensively studied.In addition,BI NLED has another impetus,since it naturally arises in the low-energy limit of open string theory [60–62].
In previous works,researchers discussed the thermodynamic properties and stability of AdS black holes with a series of nonlinear sources [63,64,20,65],and it is shown that the structures of black holes in the presence of nonlinear electrodynamics are quite different compared to the linear Maxwell theory,and its phenomenology also describes a more general case.In the work of Nam[66],the thermodynamics of dS black holes with a nonlinear electromagnetic Lagrangian was investigated in extended spacetime and with the system entropy S=Sc−S+.The stability of Reissner–Nordström dS black holes has been investigated with a linear electromagnetic Lagrangian[42,39].In this paper,we investigate the effects of the nonlinearity of a series of weak nonlinear sources on the phase transitions and critical properties of charged dS black holes.Taking the region between the black hole horizon and cosmological horizon in dS space as a thermodynamic system,M as the mass(energy),and the entropy,volume and electric charge Q as thermodynamic variables of the system,the expression of the first law is obtained on the basis of the entropy S=Sc+S+[67]and the volume V=Vc−V+[68] of the system.
The outline of the paper is as follows.In the next section,we introduce the topological black hole solutions with a weak nonlinear source and two sets of thermodynamic quantities corresponding to the BEH and CEH of dS spacetime.In the third section,we analyze the relations of the thermodynamic quantities corresponding to the two horizons,and derive the effective thermodynamic quantities of the(n+1)dimensional dS black hole with the nonlinear source.The critical state quantities and possible phase transitions of dS spacetime with the effect of the nonlinearity parameters are analyzed for n=3 in the fourth section.In the fifth section,using the Ehrenfest scheme we prove that the critical behavior belongs to second-order equilibrium phase transition.In the final section,we discuss the findings and make some conclusions.(We use the units Gd=ħ=kB=c=1).
2.Topological black hole solutions with a nonlinear source in dS spacetime
The (n+1)-dimensional action of Einstein gravity in the presence of NLED is [64]:

where R is the scalar curvature and Λ is the cosmological constant.In this action,
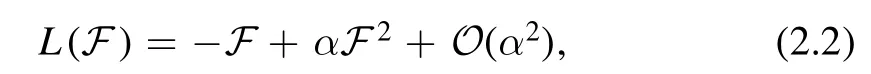
is the Lagrangian of NLED. F=Fμ ν Fμνis the Maxwell invariant,in which Fμν=∂μAν−∂νAμis the electromagnetic field tensor and Aμis the gauge potential.In addition,α denotes the nonlinearity parameter,which is small,so the effects of nonlinearity should be considered as a perturbation(α is proportional to the inverse value of the nonlinearity parameter in BI-type theories),and the series expansion for the Lagrangian is only preserved up to the first-order term of α .In this paper,we take into account equation (2.2) as the NLED source,because both BI types of NLED,in logarithmic form [69] and in exponential form [70],tend to the form of equation (2.2) for weak nonlinearity.
The(n+1)-dimensional topological black hole solutions can be written as [64],

where
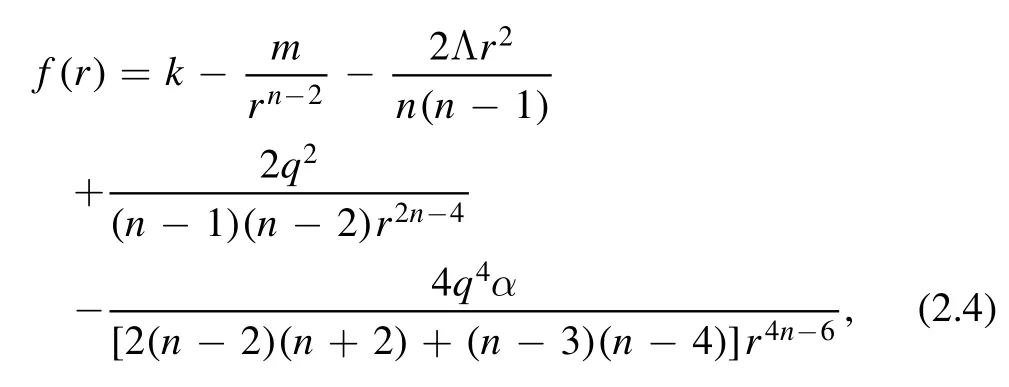
in which m is an integration constant related to the mass of the black hole,and the last term in equation (2.4) indicates the effect of nonlinearity,where only the first-order term of α is preserved.The asymptotical behavior of the solution is AdS or dS,provided that Λ<0 or Λ>0 and the case of an asymptotically flat solution is permitted for Λ=0 and k=1.
We consider asymptotically dS (Λ>0) and spherically topological black holes,which have BEH and CEH,whose positions are located at r+and rc,and f(r+,c)=0.
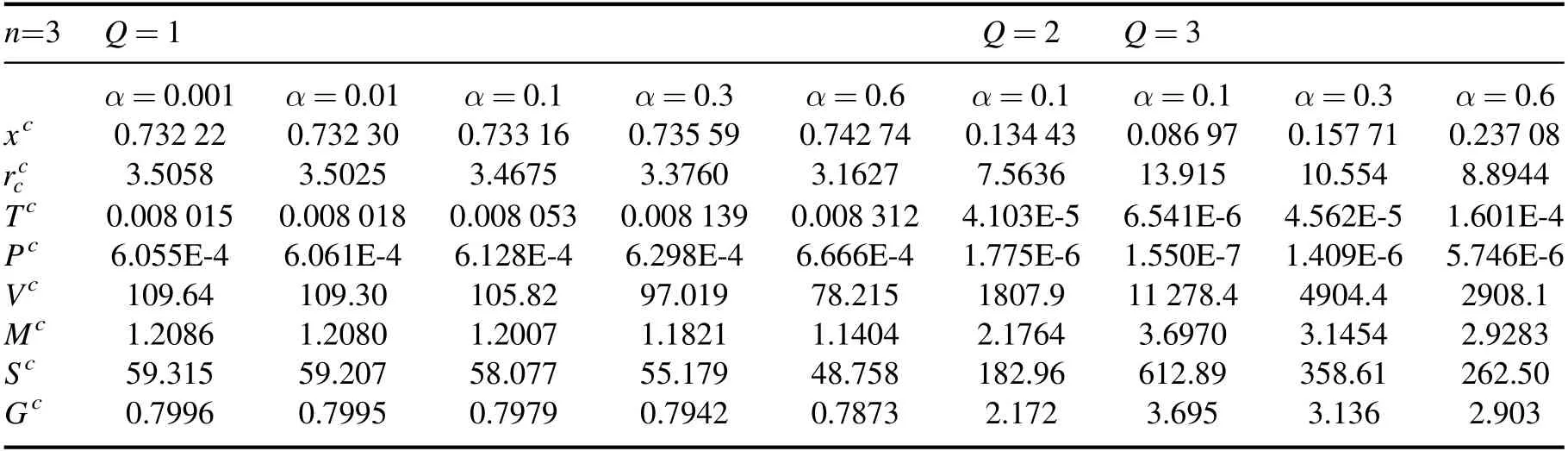
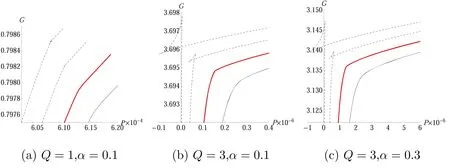
In figure 1,on each curve,the two points on the right,at which the curve intersects the horizontal axis,correspond to r+and rc,and r+ Figure 1.Black hole solution in dS spacetime with k=1,n=4,q=1,m=1.2,Λ=1 and different nonlinearity parameter α. The radiation temperatures on the two horizons,respectively,are [64], The ADM (Arnowitt–Deser–Misner) mass M and electric charge Q of the black holes are, Considering f(r+,c)=0,the mass of the black holes can be expressed by r+or rcas, The entropy and thermodynamic volume of the black holes corresponding to BEH and CEH are [67], From the perspective of extended phase space,the cosmological constant is considered as the thermodynamic pressure of black holes [71,72], From equations (2.5),(2.8),(2.9) and (2.10),two sets of thermodynamic quantities can be obtained corresponding to BEH and CEH,respectively,whose thermodynamic properties have been dealt with separately in some researches [49].They satisfy,respectively,the first law of thermodynamics, in which Φ+and Φcare the charge potentials of BEH and CEH,respectively. Two baffling problems exist with regard to the two horizons being two thermodynamic systems unless they are very far apart.First,the energy M,electric charge Q and cosmological constant Λ are the common state parameters of the two systems.Thus,the thermodynamic quantities of the two systems are not independent.Second,the black hole horizon radiation temperature T+and cosmological radiation temperature Tcpresent in equations (2.5) and (2.11) are usually different.Consequently,we take the dS space region between BEH and CEH as a thermodynamic system,but it is generally in thermal non-equilibrium.At present,a mature and general purpose method to analyze a non-equilibrium thermodynamic system has not been found.However,the fact that the two horizons possess some common state parameters reminds us that we need to build a set of effective thermodynamic quantities to investigate the thermodynamic properties of the thermal non-equilibrium system in dS spacetime. Taking the dS space region between BEH and CEH as a thermodynamic system,the thermodynamic volume and entropy of the spherically symmetric dS spacetime satisfy[67,68], Taking α as a constant and combining equations (3.1)and (3.2),one can see that the energy (mass) of the dS black hole system is a function of the entropy,thermodynamic volume and electric charge,that is: They should satisfy the first law of thermodynamics: in which T is the effective temperature,Φ is the effective electric potential and P is the effective pressure.They are conjugates of S,Q and V of dS spacetime,respectively. These effective thermodynamic quantities reflect the thermodynamic properties of the whole dS spacetime rather than that of a horizon.Therefore,they give a more comprehensive view of dS spacetime. We investigate the critical properties,phase transitions and phase structure of the spherical topology(k=1)of dS black holes with a weak nonlinear source by using effective thermodynamic quantities.According to van der Waals’ idea regarding phase transitions,we analyze the relation of the effective pressure and thermodynamic volume when the effective temperature is kept constant.And using the Gibbs free energy criterion,we discuss the phase transition of the system. When both the electric charge q and the nonlinearity parameter α are kept as constants,the critical points of the phase transition of the system can be obtained by, in which all the quantities V,T and P are functions of (rc,x)according to equations(3.1),(3.5)and(3.7).Thus,the critical quantities can be derived when Q,α and dimensionality n are given certain values.Table 1 below shows some critical values at the dimensionality n=3. Under the conditions 0 It can be seen in table 1 that with increasing α the critical values xc,critical temperature Tcand critical pressure Pcare all increasing as Q is given,and when Q is greater,they increase faster.The other critical quantities in the table are just the opposite.With the increasing of α,they decrease.Similarly,as α=0.1,xc,Tcand Pcare all increasing with increasing Q.The other critical quantities in the table decrease oppositely when Q increases.From table 1,it is shown that the nonlinearity parameters α along with the electric charge Q influence the position of the critical state.When α=0,the values of the critical quantities are consistent with those in the work [42],which is not shown in the table 1. Table 1.Critical values of effective thermodynamic quantities for different Q and α when n=3. Figure 2.Isotherms in P −V diagrams of a(n+1)dimensional dS black hole with the weak nonlinear source of n=3.Dashed lines match T Figure 2 shows that when either of the values α or Q is greater or both are greater,a more acceptable thermodynamic state exists within the smaller volume ranges and the isotherms are more like the ones of the van der Waals liquid-gas system.Thus,compared with linear electrodynamics,NLED has an effect on the phase structure of the dS black hole system.In figures 2(a),(b)and(c),when T Gibbs free energy is defined [73] as: Under the conditions 0 In figure 3,the curves for Gibbs free energy G versus effective pressure P present a swallow-tail form when T Figure 3.Isotherms in the G −P diagrams of a(n+1)dimensional dS black hole with a weak nonlinear source of n=3.Dashed lines match T According to Ehrenfest scheme,at the phase transition point,the fact that the chemical potential (molar Gibbs free energy)and its first partial derivatives are continuous but its second partial derivatives are discontinuous and divergent indicates that the phase transition belongs to second-order equilibrium phase transition.The specific heat CP,expansion coefficient β and isothermal compressibility κ of a thermodynamic system are defined by: CP−P,β −P and κ −P curves of the dS black holes with NLED for given values of Q and α are shown in figure 4 for n=3.The red thick solid lines corresponding to T=Tcare all divergent at P=Pc,so the phase transitions at the critical points belong to second-order equilibrium phase transition.Phase transitions below the critical temperature are more complex,while no phase transition is displayed by the curves above the critical temperature in figure 4. Figure 4.Isotherms in the CP −P,β −P,κ −P diagrams of(n+1)dimensional dS black holes with NLED of n=3.Black dashed lines,red thick solid lines and black thin solid lines represent T The Ehrenfest equations are: where superscripts 1 and 2 represent phases 1 and 2,respectively,and subscript q represents q remaining unchanged. According to Maxwell relations: Note that the superscript‘c’denotes the physical quantities at the critical point.By substituting equation(5.7)into(5.4)and(5.5),we get: From equation (4.1),when the independent variables are(rc,x),the critical points meet. Moreover, By substituting equation (5.9) into (5.10),one can get: To date,we have proved the validity of both Ehrenfest equations at the critical points.Utilizing equations(5.11)and(5.8),the Prigogine-Defay (PD) ratio can be calculated: Hence,the phase transition occurring at T=Tcis a second-order equilibrium phase transition. In this paper,considering the correlation of the thermodynamic quantities respectively corresponding to BEH and CEH of black holes in dS spacetime in the presence of weak NLED and taking the region between BEH and CEH as a thermodynamic system,we discuss the thermodynamic properties of the system and the effect of NLED.When M is regarded as energy (mass) of the thermodynamic system and the volume V=Vc+V+,entropy S=Sc+S+and electric charge Q are taken as the variable of dS spacetime the first law of spacetime has the same form as that of ordinary thermodynamic systems,and the effective thermodynamic quantities P,T and Φ are obtained with the first-order term of nonlinear parameter α preserved.Using these thermodynamic quantities of dS spacetime,we investigate the possible phase transitions and critical behavior of the dS black hole system,and find that nonlinearity parameter α along with electric charge Q influence the possible phase structure of a thermodynamic system.When either or both nonlinear parameter α and electric charge Q are smaller,the system has a minimum volume with physical meaning at a certain temperature T as T Acknowledgments This work is supported by NSFC under Grant No.11705107,by the doctoral Sustentation Fund of Shanxi Datong University (2015-B-10). ORCID iDs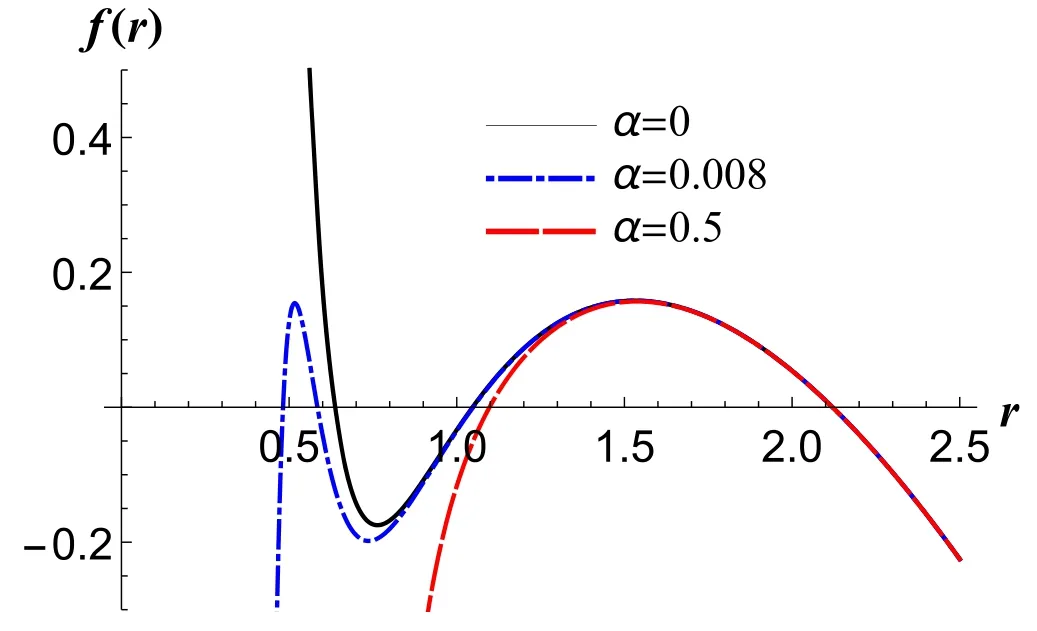
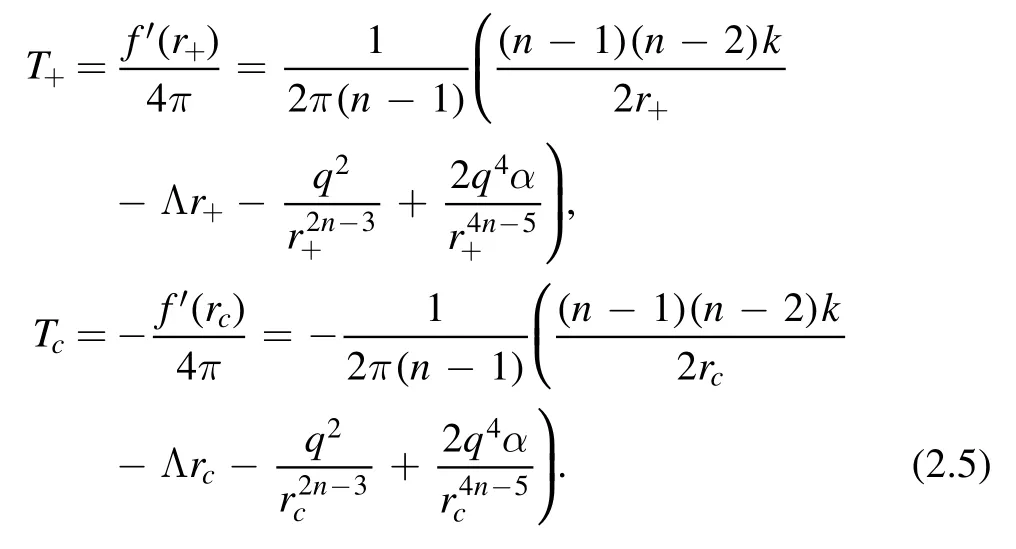
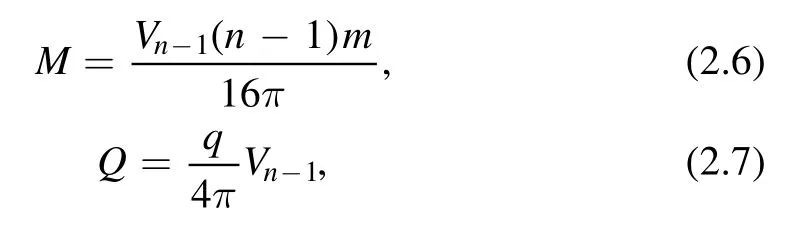




3.Effective thermodynamic quantities of a (n+1)dimensional dS black hole with a nonlinear source
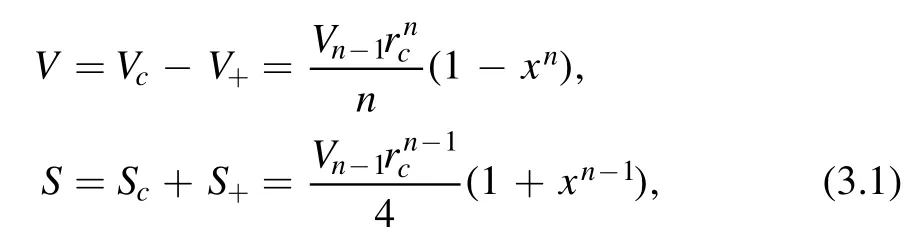
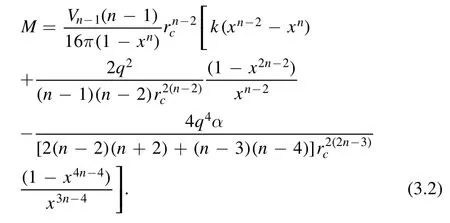




4.Critical state and phase transition in the dS black holes with the effect of NLED


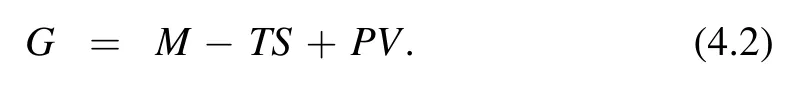
5.Analytical check of critical behavior by using classical Ehrenfest scheme




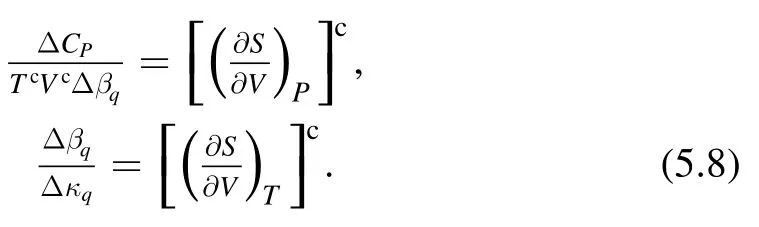

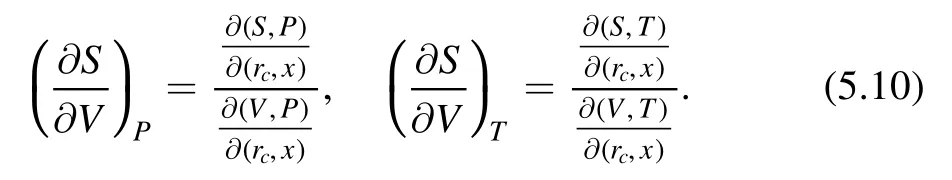


6.Discussion and conclusion
杂志排行
Communications in Theoretical Physics的其它文章
- Monte Carlo study of the magnetic properties and magnetocaloric effect of an AFM/FM BiFeO3/Co bilayer
- Grüneisen ratio quest for self-duality of quantum criticality in a spin-1/2 XY chain with Dzyaloshinskii–Moriya interaction
- Quantum corrections to the entropy in a driven quantum Brownian motion model
- On a tilted Liouville-master equation of open quantum systems
- Electron Acceleration by a radially polarised cosh-Gaussian laser beam in vacuum
- The collision frequency of electron-neutralparticle in weakly ionized plasmas with non-Maxwellian velocity distributions
