Folded novel accurate analytical and semi-analytical solutions of a generalized Calogero–Bogoyavlenskii–Schiff equation

Mostafa M A Khater,S K Elagan,M A El-Shorbagy,S H Alfalqi,J F Alzaidi and Nawal A Alshehri

1 Department of Mathematics,Faculty of Science,Jiangsu University,212013,Zhenjiang,China

2 Department of Mathematics,Obour High Institute For Engineering and Technology,11828,Cairo,Egypt

3Department of Mathematics,Faculty of Science,Taif University P.O.Box 11099,Taif 21944,Saudi Arabia

4 Department of Mathematics,College of Science and Humanities in Al-Kharj,Prince Sattam bin Abdulaziz University,Al-Kharj 11942,Saudi Arabia

5 Department of Basic Engineering Science,Faculty of Engineering,Menoufia University,Shebin El-Kom 32511,Egypt

6 Department of Mathematics,Faculty of Science and Arts,Mahayil Asir King Khalid University,Abha,Saudi Arabia

Abstract This paper studies the analytical and semi-analytic solutions of the generalized Calogero–Bogoyavlenskii–Schiff (CBS) equation.This model describes the (2 + 1)–dimensional interaction between Riemann-wave propagation along the y-axis and the x-axis wave.The extended simplest equation(ESE)method is applied to the model,and a variety of novel solitarywave solutions is given.These solitary-wave solutions prove the dynamic behavior of soliton waves in plasma.The accuracy of the obtained solution is verified using a variational iteration(VI) semi-analytical scheme.The analysis and the match between the constructed analytical solution and the semi-analytical solution are sketched using various diagrams to show the accuracy of the solution we obtained.The adopted scheme’s performance shows the effectiveness of the method and its ability to be applied to various nonlinear evolution equations.

Keywords: generalized Calogero–Bogoyavlenskii–Schiff equation,accurate analytical,semianalytical solutions

1.Introduction

The soliton is one of the most notable characteristics that characterize the integrability of the nonlinear evolution equation[1,2].Recently,stray or monster waves,weird waves,and abnormal waves have been regarded as solitary waves.Solitary waves are an uncommon type of nonlinear wave that is restricted in only one direction and has important significance in various branches of physics [3,4].These waves were first found in the deep sea[5].The applications of this wave appear in oceanography and optical fibers[6,7].Nowadays,a new type of wandering wave is known as the lumped wave,which is defined as a wave whose wandering is restricted in each direction in space [8].

Nowadays,based on the computer revolution,which has a great effect on the derivation of computational,semi-analytical,and numerical schemes,many schemes have derived,such as the sech-tanh expansion method,the auxiliary equation method,the direct algebraic equation method,the iteration method,the exponential expansion method,B-spline schemes,Kudryashov methods,the Adomian decomposition method,Khater methods,-expansion methods,and so on [9–15]; in addition,the lump solutions of many nonlinear phenomena have been investigated [16–20].

In this context,our paper aims to study the new solitonwave solutions of the generalized CBS equation through the perspective of ESE,and MKud analysis technology [21,22].Another goal of the manuscript is to limit the examination of the semi-analytical and numerical solutions of the considered model to an explanation of the accuracy of the analytical solutions obtained and the analytical schemes used [23,24].The generalized CBS equation is given by [25–30]:

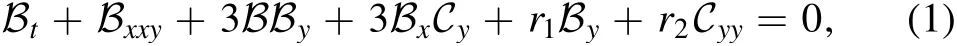
where B = B (x,t,t),C =C(x,y,t) describe the dynamics of solitons and nonlinear waves,while ri,i=1,2 are arbitrary constants to be determined later.Using the next relation betweenC &B in the following formula,B= Cx,yields

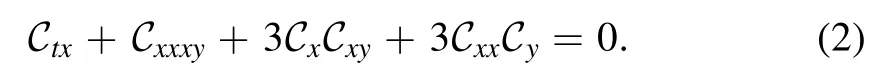
Eq.(2) is given in (2+1) dimensions,and has the following formula

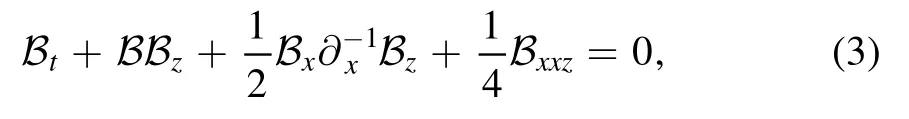
while the potential form is given by

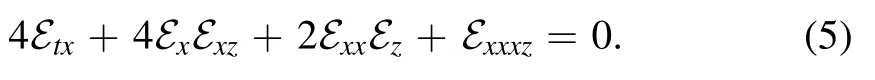
Equations (2),(4),and (5) describe many nonlinear phenomena in plasma physics.Employing the next wave transformation C = C(x,y,t) =S( P) ,where P=r1x+r2y+r3tand ri,i=1,2,3 are arbitrary constants,converts equation(2)into the following ordinary differential equation.Integrating the obtained equation once with the zero constant of integration,we get:

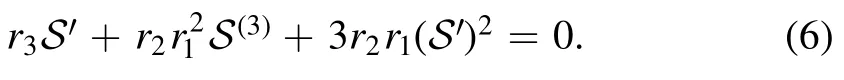
Handling equation (6) through the perspective of the abovementioned analytical schemes and the homogeneous balance principle gives n=1.Thus,the general solutions of equation(6)are evaluated by

where a0,a1,and a−1are arbitrary constants.

The other sections of this manuscript are as follows:section 2 studies the general solution of the generalized CBS model.In addition,the accuracy of the obtained solution is checked using the abovementioned semi-analytical scheme.Section 3 introduces the solutions and achieves the goals of our research paper.Section 4 provides a summary of the manuscript.

2.Comparison of analytical and semi-analytical approaches to the generalized CBS equation

This section studies the analytical,semi-analytical,and numerical simulation of the generalized CBS equation.The headings of this section can be summarized in the following order:

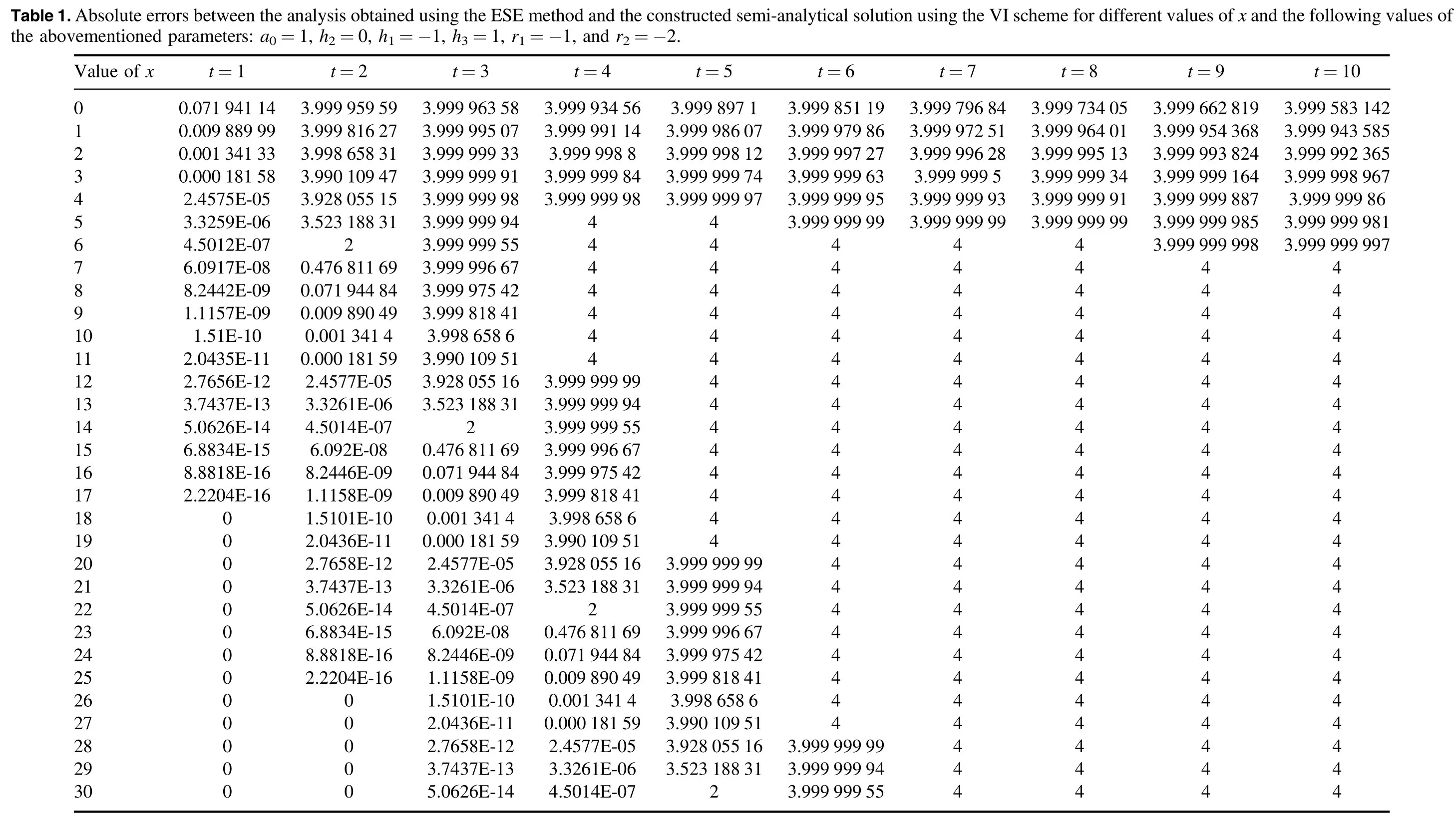
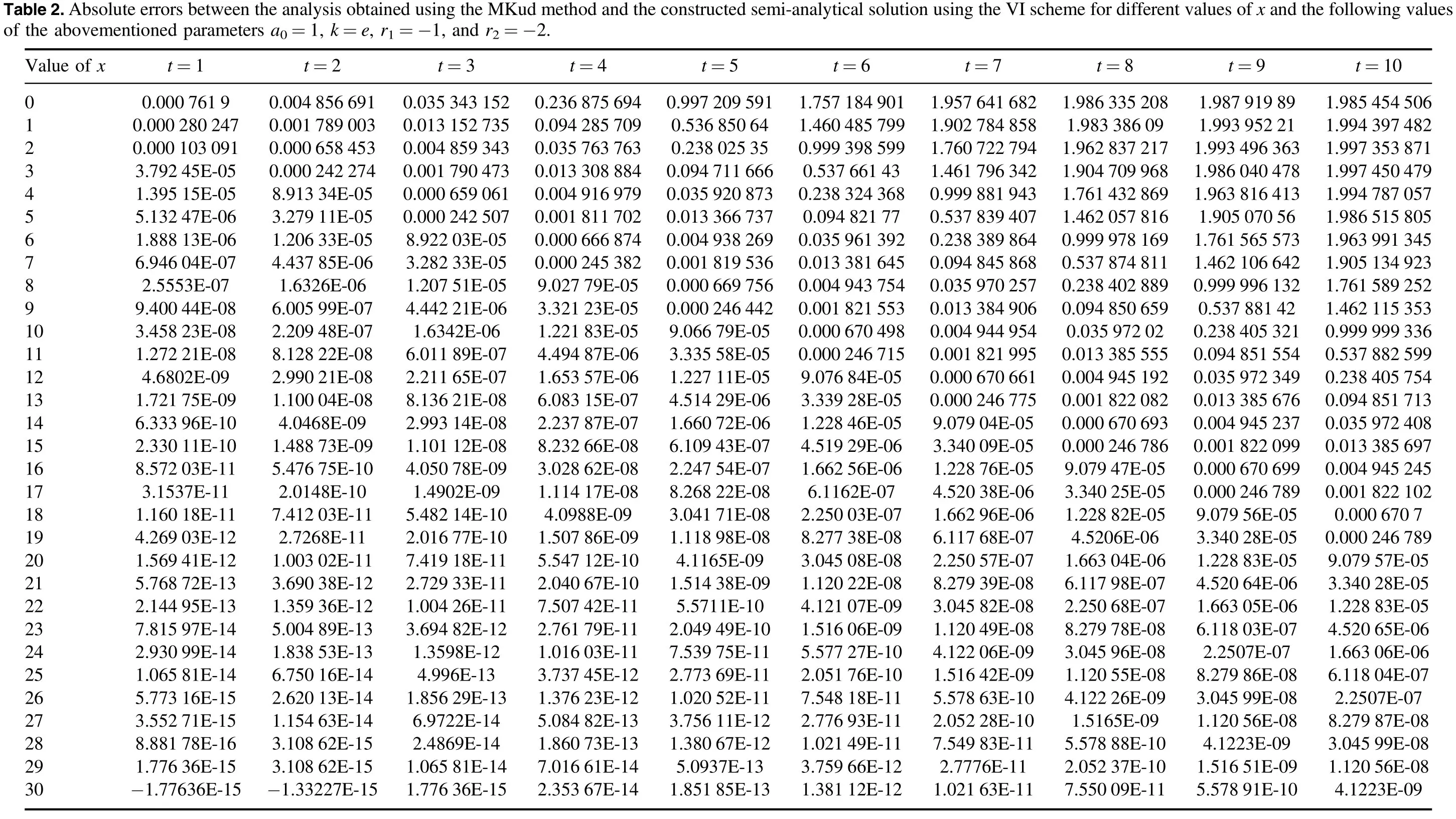
• We apply the ESE and MKud schemes to equation(6)to get solitary-wave solutions,then obtain the initial and boundary conditions to investigate semi-analytical solutions through the VI technique.

• We check the accuracy of the obtained solution and calculate the absolute error value between the exact and semi-analytical solutions.

2.1.ESE analytical vs.VI numerical techniques,along with the generalized CBS equation

Applying the ESE scheme’s framework and its auxiliary,( C′ ( P) =h3C ( P)2+h2C ( P) +h1)(where hi,i=1,2,3 are arbitrary constants to be determined later),to equation (6)obtains the following sets of abovementioned parameters:

Set I

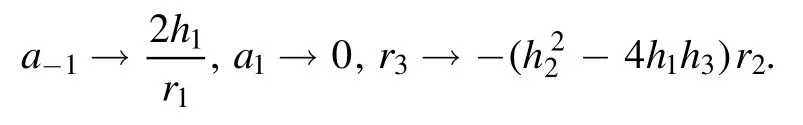
Set II

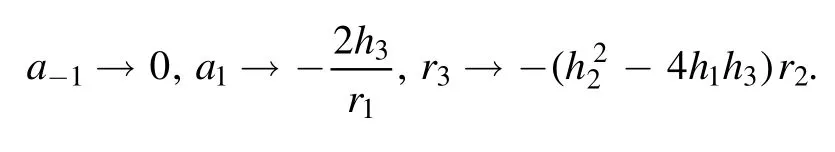
Therefore,the solitary solutions of the considered model are constructed in the following formulas:

For h2=0,h1h3>0,we get

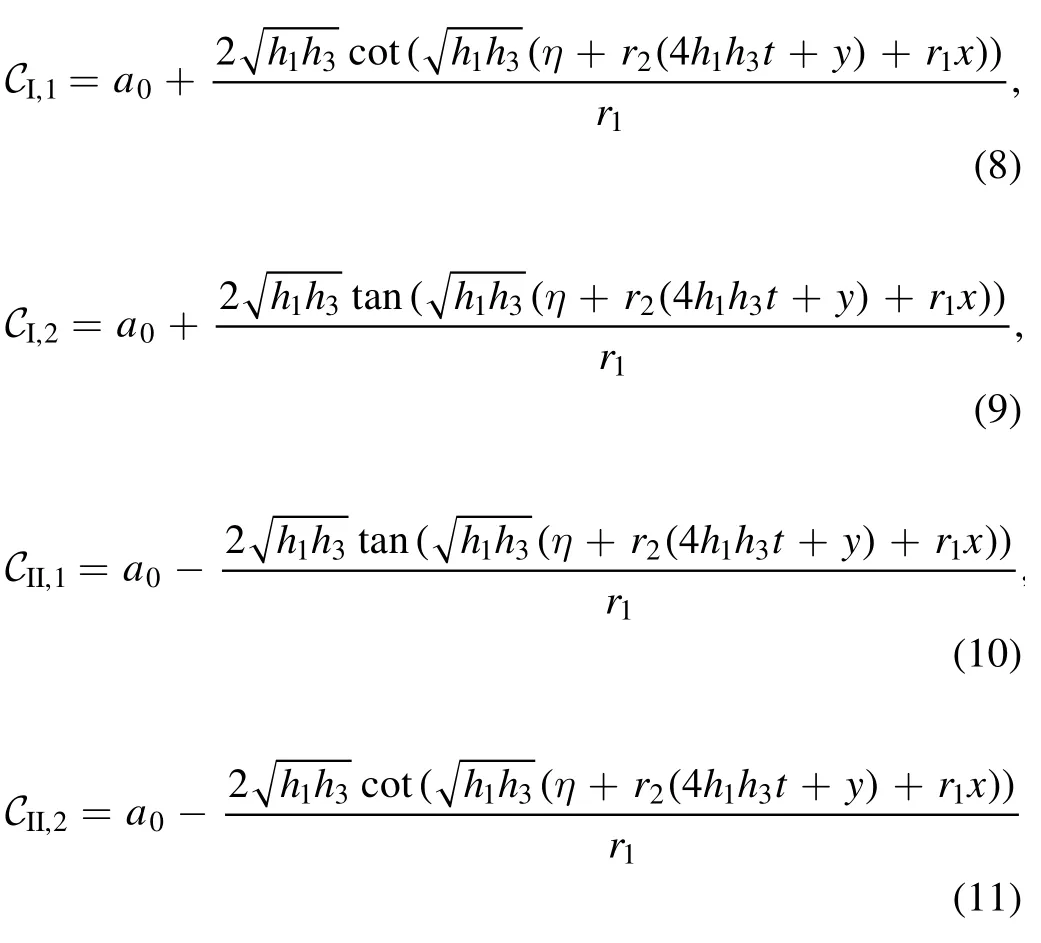
For h2=0,h1h3<0,we get

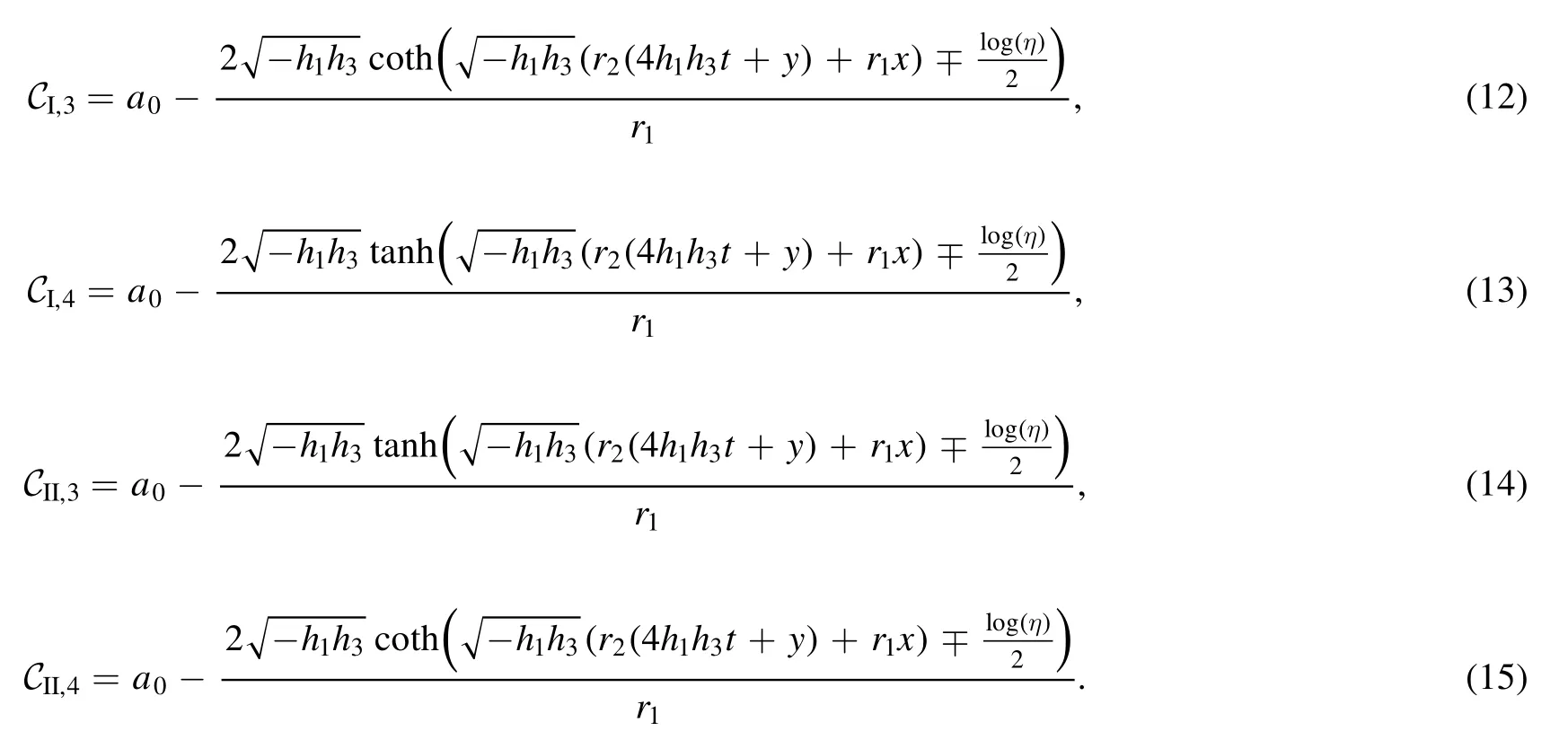
For h1=0,h2>0,we get

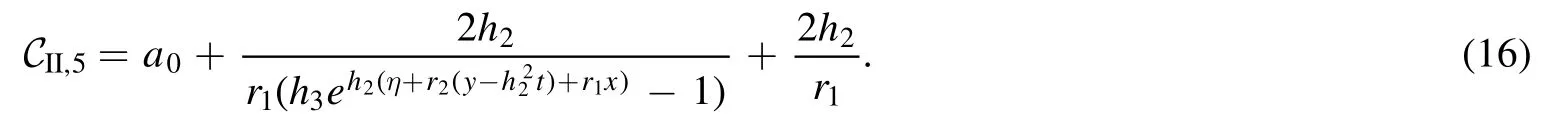
For h1=0,h2<0,we get

For4h1h3>we get

2.1.1.Comparison of the analytical and numerical solutions.Applying the VI method to equation (2),we get the following semi-analytical solutions:

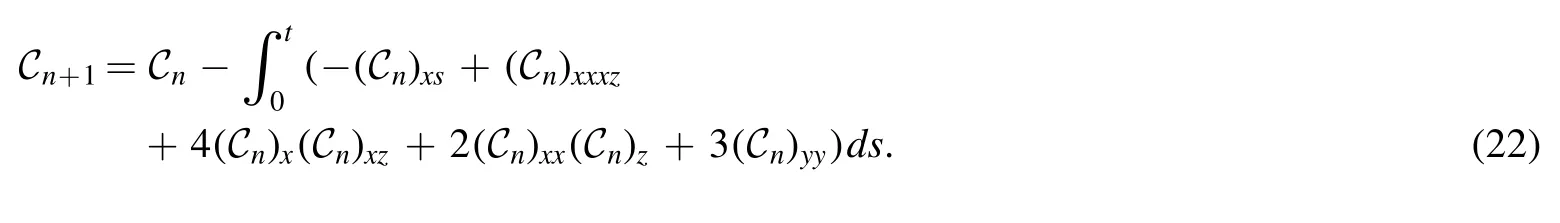
Using equation (22),

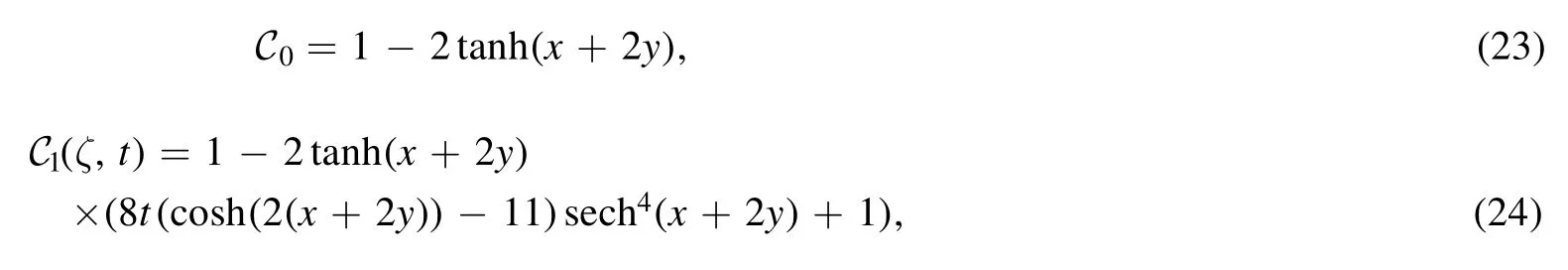
Using same steps,we can getCi,i=3,4,5,….

2.2.MKud analytical vs.VI numerical techniques,along with the generalized CBS equation

Applying the MKud scheme’s framework and its auxiliary,( L′ ( P) = ln (k)( L ( P)2-L ( P) ))(where k is an arbitrary constant to be evaluated later),to equation (6) obtains the following sets of abovementioned parameters:

Set I

?

?

Therefore,the solitary solutions of the considered model are constructed in the following formula:

2.2.1.Comparison of the analytical and semi-analytical solutions.Applying the VI method along with equation (22) to equation (2),one obtains

Using same steps,we can getCi,i=3,4,5,….

3.Interpretation of the results

This section highlights the novelty of our research papers.It also shows the accuracy of the analytical solution obtained.The ESE and MKud calculation schemes have been applied to the generalized CBS equation for the constructed solitarywave solution.Many different wave solutions have been obtained,some of which are demonstrated in 2D,3D,and some sketches in profile drawings to explain solitary waves’dynamic behavior in nonlinear phenomena in plasma physics.Figures 1 and 3 show the periodic-kink solitary-wave solution.While figure 2 show the semi-analytical solution in three different forms (2D,3D,and contour plots).Comparing our solution with the solutions obtained in previously published papers,it can be seen that our solution is completely different from the solution evaluated in [25–29].

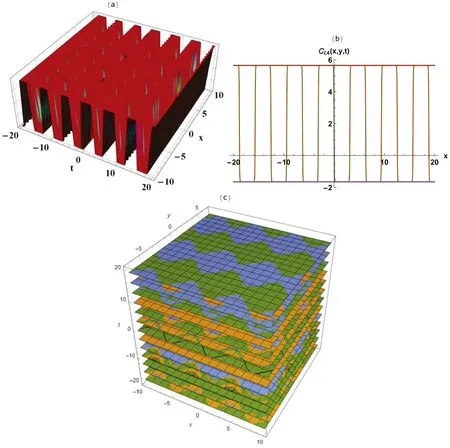
Figure 1.Solitary-wave-solution equation (13) in 3D,2D,and contour plots.

Figure 2.Semi-analytical solutions of equation (6) in 3D and contour plots.

Figure 3.Solitary-wave solutions of equation (26) in 3D,2D,and contour plots.

The VI scheme was applied to the considered model based on the computational solution obtained.The absolute error between the analytical and semi-analytic solutions was calculated,to show the accuracy of the solution and the method used (tables 1 and 2 and figures 3 and 4).This calculation shows that the MKud method is superior to the ESE method,and its absolute error value is much smaller than the absolute value obtained by the ESE method (figure 5).

Figure 4.Semi-analytical solutions of equation (2) in 3D and contour plots.

Figure 5.Absolute errors between the ESE and MKud analytical schemes and the TQBS numerical scheme.

4.Conclusions

This research paper has successfully processed the generalized CBS equations generated for plasma physics and weak dispersion media.The ESE,MKud,and VI schemes were used to find accurate and novel solitary-wave solutions for the model under consideration.Three different types of sketch were used to represent the kink solitary-wave solution.The accuracy of the MKud method was verified using the ESE method.This is our fourth paper on the topic of the ESE method,which examined the accuracy of the calculation scheme.This series aims to determine the accuracy of all the calculation schemes.

Acknowledgments

This research was supported by Taif University Researchers Supporting Project Number (TURSP-2020/247),Taif University,Taif,Saudi Arabia.Additionally,the authors extend their appreciation to the Deanship of Scientific Research at the King Khalid University,Abha,KSA,for funding this work through research group under grant number (RGP.2/121/ 42).

Availability of data and materials

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Competing interests

The authors declare that we have no competing interests.

Authors’ contributions

The authors have contributed equally to the design and implementation of the research,to the analysis of the results,and to the writing of the manuscript.