基于SG算法的MEMS加速度传感器信号恢复研究

2021-10-13纪莲和王文赫聂琪鹤郑平平

机械与电子 2021年9期

纪莲和，王文赫，王建，聂琪鹤，郑平平

(北京智芯半导体科技有限公司，北京 100192)

0 引言

传感器被广泛应用于工业以及医疗卫生等领域中，是生产自动化和科学化不可或缺的基础步骤[1-2]。传感器位于系统前端以获取信息，对系统产生影响的主要因素为设备的综合性能和输出信息的安全性[3]。如果传感器在使用的过程中出现故障，会导致系统性能下降和误差累积，严重时还会导致整个系统瘫痪。因此，需要及时检测传感器故障，对信号进行恢复。

本文在文献[4]和文献[5]的基础上，结合SG(Savitzky-Golay)算法，提出一种基于SG算法的微机电系统(microelectro mechanical systems，MEMS)加速度传感器信号恢复方法。

1 方法

1.1 基于SG算法的信号去噪

集合经验模态分解(ensemble empirical mode decomposition，EEMD)的基本思想，就是采用白噪声的频谱分布获取各MEMS加速度传感器信号对应的尺度参数。根据白噪声的主要特性，经过多次操作，最终使其相互抵消，达到去噪的目的，详细的信号去噪流程如下所述。

a.设定原始信号为x(t)，对应的加权均值为0，高斯白噪声ni(t)是由幅值和标准方差组成，叠加次数为M，则有

xi(t)=x(t)+ni(t)

(1)

b.对xi(t)进行经验模态分解(empirical mode decomposition，EDM)，获取N个IMF，将其表示aij(t)，余项表示为ri(t)。

c.将相互之间不存在任何关联的随机序列统计值设定为0，通过计算各个固有模态函数分量(intrinsic mode function，IMF)的平均取值，减少噪声对真实IMF产生的影响[6]，IMF的平均值计算式为

(2)

aj(t)为对原始信号经过多次分解后获取的第j个IMF。

小波变换是最近几年使用比较多的一种去噪方法，尤其是针对白噪声，去噪效果更加理想。所以，构建小波-SG模型对信号进行去噪处理，可以有效减少随机白噪声和局部脉冲对信号产生的影响。

小波-SG算法的具体操作步骤如下所述。

a.对含噪信号进行尺度分解，获取对应的小波分解系数，具体的计算公式为

(3)

cj,k为信号的近似系数；dj,k为信号细节系数；h为滤波器的脉冲响应范围[7-8]；j为响应分解尺度。

b.为了有效抑制脉冲干扰，对cj,k和dj,k进行SG平滑处理。设定研究对象为近似系数c1,k，设定ci为任意一个小波系数，在ci附近拟合nl+nt+1个点在最小二乘意义下的多项式pi(c)，其中pi(c)在ci的取值即为光滑系数gi，具体的表达形式为

(4)

bp为多项式系数；p为ci各个点的数量。

设定实测数据yi，为了使pi(c)和测试数据充分拟合，结合bp，促使式(5)达到最优。

(5)

nr为拟合系数的取值范围；cj为在ci处的第j个幅值取值。

c.保持经过平滑处理的小波系数不变，基于式(6)阈值量化小波系数。

(6)

dj(i)为白噪声的方差取值范围；Tj为浮动阈值。

d.将经过上述操作步骤处理后获取的近似系数和细节系数进行重构[9]，具体的计算式为

(7)

cj,n为核函数；hk-2n和gk-2n分别为训练样本和测试样本的数量。

通过上述分析，将3种算法进行结合，形成小波-SG-EEMD算法。基于SG算法的信号去噪流程如图1所示。

图1 基于SG算法的信号去噪流程

将被分解的MEMS加速度传感器信号x(t)优先通过小波-SG进行预处理；EEMD分解预处理的信号，重构IMF分量，最终实现信号去噪。

1.2 MEMS加速度传感器信号恢复

结合图信号理论，将经过去噪的MEMS加速度传感器信号恢复设定为图信号x={x(n)}∈RN，x(n)为传感器vn的信号值[10]，其中图模型能够表示为

G=(V,E,W)

(8)

V为传感器节点集合；E为模型的边数集合；W代为邻接权矩阵。

图像傅里叶变换能够表示为

(9)

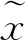
其中，x满足的约束条件为

(10)

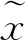
将MEMS加速度传感器信号设定为矩阵的形式，即

F={fn,t}∈RN×T

(11)

{fn,t}为信号vn在时间t的信号取值大小。信号矩阵F按照列向量处理之后得到网络数据向量f∈RN×T。

在上述分析的基础上，将经过去噪处理信号的时间域平滑特性和空间平滑特性结合，构建联合图域模型，具体的操作步骤如下所述。

a.构建MEMS加速度传感器信号的空间域图模型为

GS=(VS,ES,WS)

(12)

VS为传感器节点信号；ES为有边连接；WS为权矩阵，矩阵中的元素能够表示为

(13)

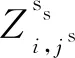
b.构建MEMS加速度传感器信号的时间域图模型为

GTI=(VTI,ETI,WTI)

(14)

VTI为信号节点集合；ETI为边的集合；WTI为传感器中未丢失节点集合的信号数据。首先，需要估计出采样时刻t的参考数据φ，公式为

(15)

(16)

以上2种模型间的信号均具有关联性，但是二者对于“关联信号”的定义完全不同。其中，时间域中的相邻信号是指在设定采用时间内的相邻时刻[14-15]；而空间域则是指相邻信号之间地理距离较近的传感器数量。为了更好地完成信号恢复，将都具有“相邻信号”的二者进行组合，形成联合域图模型。同时引入图全变分最小准则进行信号恢复，具体的操作步骤为：①优先通过相邻信号节点设计出一种联合图域网络信号平滑度强弱方法；②将步骤①中的方法作为依据，构建含有对应约束条件的数学模型，最终使图全变分最小；③最终结合优化模型设计信号恢复方法，有效实现MEMS加速度传感器信号恢复。

在MEMS加速度传感器信号恢复过程中，通过图全变分进行信号处理，其中具体的表达形式为

(17)

xr为信号vr的数据值；xz为信号vz的网络节点集合；wr,z为2个节点之间的权重。

为了能够更好融合信号的特性，需要在方法中引入联合图全变分，具体的表达形式为

(18)

‖X-P′X‖为向量的范数。

将式(18)的MEMS加速度传感器信号恢复问题转换为如式(19)所示的优化模型，即

(19)

另外，信号每一次在修复的过程中需要计算复杂度，同时全面考虑信号的空间和时间平滑性。

结合式(19)对MEMS加速度传感器信号进行恢复，则有

(20)

2 仿真实验

为了验证所提基于SG算法的恢复方法的有效性，进行仿真实验。待测加速度传感器和标准传感器同时固定在载具上，进行冲击测试，记录每次测试标准传感器的加速度值，通过示波器采集被测传感器的输出信号。

实验内容具体如下：在不同丢失比例下，优先对比3种方法的信号恢复质量，衡量指标包括均方根误差、平均绝对误差和迭代次数。不同方法的信号恢复质量对比如图2所示。

图2 不同方法的信号恢复质量对比

分析图2中的实验数据可知，当测试样本开始持续增加，各个信号恢复方法的均方根误差、平均绝对误差和迭代次数均发生了明显的变化。其中，两者误差的取值越低，迭代次数越少，说明信号的恢复结果和真实结果越接近。由于本文方法在信号恢复前期，通过SG算法对信号进行去噪，有效剔除冗余信号，确保信号的恢复质量得到有效提升。

在不同的丢失比例下，重点对比3种不同方法的信号恢复速率，实验结果如表1所示。