地铁振动作用下高层建筑物边墙的动态响应规律分析

吴克凯

(北京市大兴城镇建设综合开发集团，北京 102600)

1 工程概况

地铁8号线中国美术馆站站后折返线区间全线采用矿山法施工。此区段区间为直线段，并以2‰的坡度下坡。左右线区间结构水平净距为3.2 m，区间主要结构参数如表1所示。

2 振动效应模拟计算

2.1 结构参数

隧道衬砌材料参数如表2所示，隧道衬砌采用C35混凝土。

2.2 模型建立

考虑到模型计算的空间效应，计算模型取取长400，宽150 m，自地表50 m厚的土体作为计算范围。

2.3 振动波

振动波振幅为0.01 m/s，振动时长π/10s，振动周期T为π/300。振动波加载至轨道相应位置。提取建筑物中相应位置质点的振动峰值速度。

3 振动数据分析

建筑物侧墙内选取13个质点，各个测点振动速度值如表3所示。

由图1所示曲线可知，建筑物侧墙水平向振动响应规律主要为振动速度随振源距离的增加出现往复循环变化，此时的振源距为质点高差，因此可以获得，随高差的增加水平向振速并不是一味增加或降低，而是随高差表现出了放大和衰减双重特性。

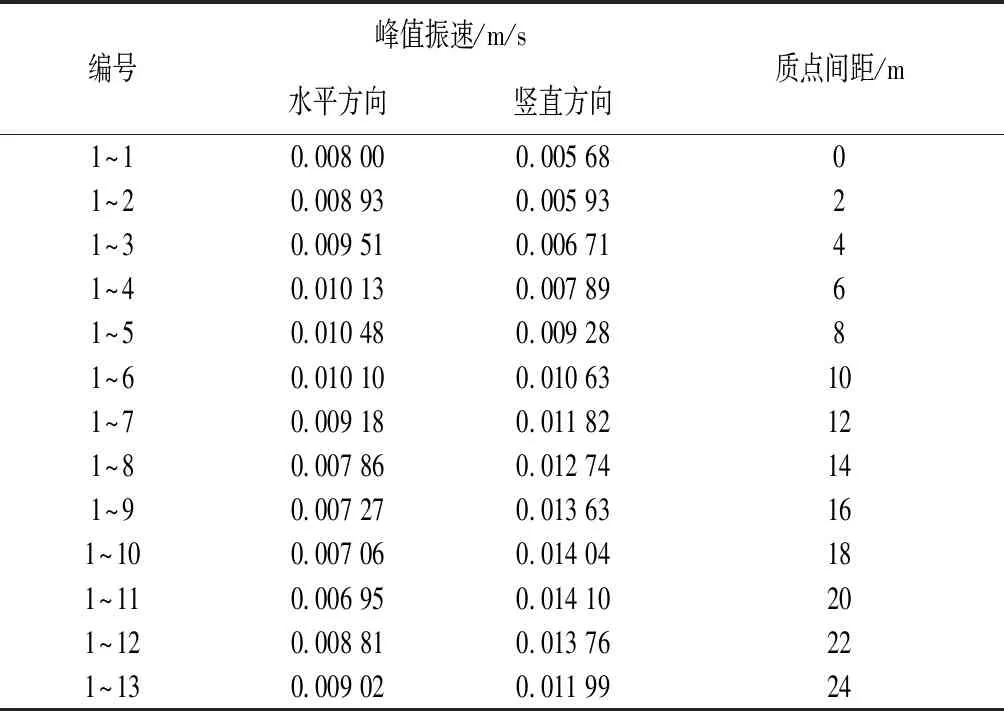
表3 质点峰值振动速度

图1 水平方向质点峰值振动速度变化规律

图2中所示曲线为边墙质点竖直向振动峰值的变化曲线，曲线显示竖直向振动在高程达到一定值时，呈现逐渐加大的规律，此阶段内振动速度主要受高程放大效益作用，在局部位置随高程增加不断加大，由振速值可以看出，竖直向振速放大倍数远大于水平向，放大倍数近3倍。

图2 竖直方向质点峰值振动速度变化规律

通过研究发现高程放大和距离衰减效应共存，高程增加时，意味着振源距持续增加，高程放大效应是在一定高度内凸显，即在一定高度内距离的衰减效应小于高程放大效应，但当高度增加到一定限制时，振动速度仍是呈衰减趋势。此限制于振动频率相关。由此，对不同高程处质点速度峰值拟合需考虑高程与振源距离两个因素。振速与高程和振源距的数学关系可以通过下式进行描述。

式中：R为振源距离，m；α为衰减系数；K″为与岩性相关的系数。K′为与结构材料性质相关的系数；H为高差，m；β为放大因子。

4 结 论

(1)建筑物侧墙水平向振动响应规律主要为振动速度随振源距离的增加出现往复循环变化，随高差的增加水平向振速并不是一味增加或降低，而是随高差表现出了放大和衰减双重特性。

(2)竖直向振动在高程达到一定值时，呈现逐渐加大的规律，此计算模型中振动速度主要受高程放大效益作用，在局部位置随高程增加不断加大，竖直向振速放大倍数远大于水平向，此模型中放大系数近3倍。

(3)高程放大效应和距离的衰减效应共存，对不同高程处质点速度峰值拟合需考虑高程与振源距离两个因素。