高层建筑物内部结构的地铁振动放大与衰减规律

姜 磊

(北京市首都公路发展集团有限公司，北京 100073)

1 振动计算模型

1.1 结构参数

地下线区间地层土主要由杂填土、砂质粉土、细中砂、卵石和黏土构成，主要物理力学参数如下所示。

表1 地下线区间地层土力学参数

隧道衬砌材料参数如下表所示，隧道衬砌采用C35混凝土。

表2 隧道衬砌力学参数

1.2 模型建立

考虑到模型计算的空间效应，计算模型取取长400，宽150 m，自地表50 m厚的土体作为计算范围。计算模型如图1所示。

图1 计算模型

2 振动数据分析

建筑物楼层内部取个9质点。各个测点振动速度值如表3所示。

表3 质点峰值振动速度

水平和竖直两个方向的振速变化曲线都已经出现振动放大现象。峰值点振动速度的放大倍数约为1.2倍。但随着距离的增加，峰值点逐渐降低，图中整体曲线变化趋势为降低，说明距离的衰减效应对振动速度仍产生作用，减弱高程的放大作用。而位于同一层地板结构内的质点振动效应随距离的增加逐渐减弱，在室内墙角位置振动速度最小，建筑结构边角处的结构夹制作用显著。

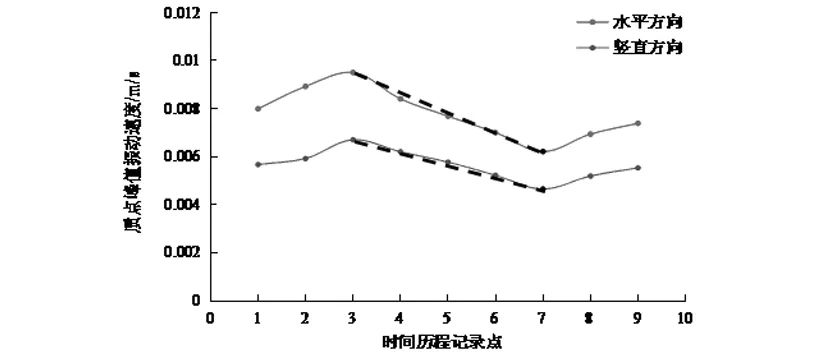
图2 质点峰值振动速度变化规律

如图2所示，其虚线标注部分为同高程的质点振动速度衰减变化曲线。根据质点振动速度变化特征，建立一个影响振动速度大小，与结构夹制作用有关的同时与结构外侧墙边界距离相关的夹制作用因子，当质点位于侧墙边界时，距离为0，此时的夹制作用影响忽略，则可以建立模型为

(1)

式中：r为距离侧墙边界的距离，m；ε为结构夹制作用因子，数值大于1。

对建筑物内质点振动速度与距离进行数据分

析，得到夹制因子的变化特征。质点水平振动速度结构的夹制因子如表4所示。

表4 质点峰值振动速度结构夹制因子拟合结果

振动速度与夹制因子拟合相关系数R2均大于0.9。

不同高程处质点速度峰值的变化规律即对结构侧墙质点进行研究。根据质点振动速度随高程增加的特征，振速与高程的数学关系可以通过指数函数进行描述。

V′=K′·eβ·H

(2)

式中：V′为振动速度峰值，m/s；K′为与结构材料性质相关的系数；H为高差，m；β为高程放大因子。

对建筑物内质点水平方向和竖直方向的振动速度与高程进行数据分析，得到高程放大因子的变化特征。振动速度高程的放大因子如表5所示。

振动速度与高程的拟合相关系数R2均大于0.9。

通过对数值模拟结果分析发现建筑物内部的质点振动响应特征主要呈现为随高程增加的放大效应和因夹制作用的衰减效应。两者均受建筑结构形态的影响。

表5 质点峰值振动速度高程放大因子拟合结果

4 结 论

(1)高层建筑物内质点峰值振动速度随高程增加峰值振动速度呈现放大的变化特征，振动速度与高程的数学关系可以通过指数函数进行描述。

(2)建筑物内部质点由于受结构夹制作用影响，质点振动速度随夹制作用增强而衰减，夹制作用与距离结构边缘距离相关，当质点位于边缘时，距离为0，此时的夹制作用影响忽略。

(3)建筑物内部的质点振动响应特征主要呈现为随高程增加的放大效应和因夹制作用的衰减效应。两者均受建筑结构形态的影响。