考虑乘客满意度的轨道交通列车行车间隔研究

2021-10-13杨蓉，聂垚，雷莹

黑龙江交通科技 2021年9期

关键词：换乘站台间隔

杨蓉，聂垚，雷莹

(1.重庆轨道交通(集团)有限公司，重庆 400074：2.安徽国防科技职业学院，安徽六安 237000)

1 行车间隔与满意度关系模型

1.1 行车间隔方差分析

假定轨道交通线路为n条，行车间隔用来表示，分析r个不同的行车间隔对乘客满意度y的影响，yij表示行车间隔为ti的第j条轨道线路乘客满意度，建立线性单因子方差分析的数学模型

(1)

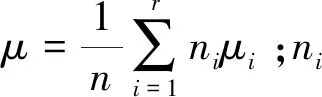
(2)

SP=SE+SA

(3)

(4)

(5)

式中:SE示行车间隔相同时乘客满意度与其平均值之间的差异，为随机误差项，SA同行车间隔时乘客满意度的均值与总体乘客满意度的均值之间的偏差平方和，即因素A的效应平方和。根据式(1)、(2)得E(SA)=(y-r)σ2，当SA、SE相互独立且H0成立时可得

(6)

其中:F为H0的检验统计量，对给定显著性水平α，若F>Fα[r-1,r(n-1)]，则表示行车间隔对乘客满意度具有显著影响，反之则无。

1.2 不同站台形式的行车间隔与满意度关系模型

y为乘客满意度，t为行车间隔，同时考虑轨道车站站台形式对乘客满意度的影响，分为岛式站台、侧式站台和岛侧混合式站台共计三类。行车间隔为定性变量，需进行数量化处理，引入3个虚拟变量，用以处理三种不同站台形式

因站台形式共计三类，所以3个变量之和恒为1，即P1+P2+P3=1，为解决变量间出现多重共线性问题，需去掉1个0～1型变量，保留2个0～1型变量。随机选择去掉变量P1，只保留变量P2和P3。

假设在行车间隔对满意度的回归模型中，三种不同的站台形式有相同的斜率和不同的截距，则有如下模型

yi=α0+α2P2j+α3P3i+α4xi+εi

(7)

式中：yi为乘客满意度，ti为行车间隔；P2i=1为侧式站台，P3i=1为岛式站台，在虚拟变量赋值时将侧式站台作为基准站，截距α0为分离式换乘的截距。

1.3 不同轨道车站性质的行车间隔与满意度关系模型

考虑轨道车站性质和行车间隔对乘客满意度的影响，按车站运营性质可分为公中间站、折返站、换乘站、终点站，将轨道车站为定性变量。引进4个虚拟变量，以处理四种不同的轨道车站性质

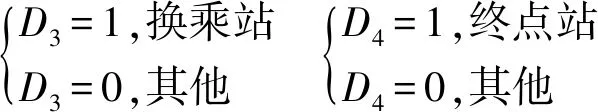
模型(7)一样，消除模型中多重共线性问题，需保留3个0～1型变量，随机选择去掉D1，只保留D2、D3、D4。

假定在行车间隔对满意度的回归中，四种不同的轨道车站性质有相同的斜率和不同的截距，则有如下模型

yi=β0+β2D2i+β3D3i+β4D4i+β5xi+εi

(8)

式中：yi为乘客满意度，ti为行车间隔；D2i=1为折返站，D3i=1表示换乘站，D4i=1为终点站，在虚拟变量赋值时将中间站作为基准站，截距β0为中间站的截距。

2 案例分析

2.1 数据选取

以重庆轨道交通为例，截止2020年2月底共计开通运营线路8条，轨道交通正常运营时，列车最小行车间隔2 min30 s，最大行车间隔15 min，其中轨道车站共计170座(换乘站不重复计算)。根据线网列车运行交路情况，对不同区间乘客满意度进行调查，实际调查行车间隔为轨道交通运营组织方案中理论列车开行时间，乘客满意度根据乘客评分所得，评分标准为：1分—非常不满意，2分—不满意，3分—一般，4分—满意，5分—非常满意。具体调查统计分析结果如下(除4号线外，轨道交通工作日高峰、平峰以及双休日行车间隔存在一定差异)：

(1)站台形式。因不同线路车站站台形式不同，现共计开通190个轨道车站(换乘车站重复计算)，其中岛式站台为100个，占比52.63%，侧式站台为90个，占比47.37%。

(2)轨道车站性质。中间站、折返站(现使用折返站)、换乘站和终点站所占比例分别为65.88%、14.12%、11.18%和8.82%，各类车站平均行车间隔满意度评分分别为3.8分、3.5分、3.2分、3.3分和3.4分，由此发现轨道车站性质并不是影响乘客满意程度的唯一因素，同时受到其他条件的制约。

(3)行车间隔。重庆轨道交通工作日高峰时段最小平均间隔5 min25 s，平峰时段最小平均间隔为6 min40 s，高平峰时段均有62.5%线路在最小行车间隔均值内；双休日最小平均行隔为6 min22 s，其中50%线路最小平均行车间隔在均值内，随着行车间隔的增加乘客满意度评分逐渐降低，当行车间隔达到10 min时，满意度出行明显的下降，平均满意度仅有2min。

(4)乘客满意度。乘客行车间隔满意度评分平均值为3.5分，72.63%车站的行车间隔小于5 min，乘客满意度评分为4.2分，12.11%车站行车间隔为10 min，乘客满意度评分仅为2.8分。说明列车开行间隔5 min左右可以使较多乘客感到满足，同时行车间隔的增加将会使乘客满意度出现下降。

2.2 模型计算

为分析行车间隔与乘客满意度的关系，研究行车间隔变化时对乘客乘车满意度的影响，选取调查样本中行车间隔和乘客乘车满意度评分数据进行统计分析，得到概率值P=0.01显著性水平下的单因子方差分析结果：检验统计量值为2.736，根据F分布表可知F0.01(7.19)=1.72，F>F0.01(7.91)，表明400个样本车站的乘客满意度评分在不同行车间隔的影响下，存在显著性差异。行车间隔与乘客满意度的相关性较高，行车间隔对乘客满意度具有显著影响。

用普通最小二乘法求解模型(7)和(8)，其中模型因变量均为乘客满意度，模型1自变量为站台形式和行车间隔，模型2自变量为轨道车站性质和行车间隔，计算结果如表2～表4所示。

表1 模型系数及误差

由表1可知模型1与模型2的相关系数分别为0.993和0.994，表明不同的轨道车站形式和轨道车站性质可能会直接影响乘客乘坐轨道交通时的满意程度。拟合优度取值越接近1，说明模型样本数值的拟合程度越好，反之则拟合程度越差。模型1的拟合优度为0.991，表明轨道车站形式和行车间隔对乘客满意度的影响程度高。模型2的判定系数为0.988，表明轨道车站性质和行车间隔对乘客满意度的影响程度高。模型1和模型2估计值的标准误差均不到1.4，说明模型拟合优度良好。

表2 模型方差分析

表2为模型1和模型2的方差分析结果，其中两个模型回归方程F值的P均为0.000，说明线性回归方程显著，分别说明了轨道车站形式、行车间隔与乘客满意度有显著的线性关系，同时轨道车站性质、行车间隔与乘客乘坐轨道交通的满意度也有显著的线性关系。

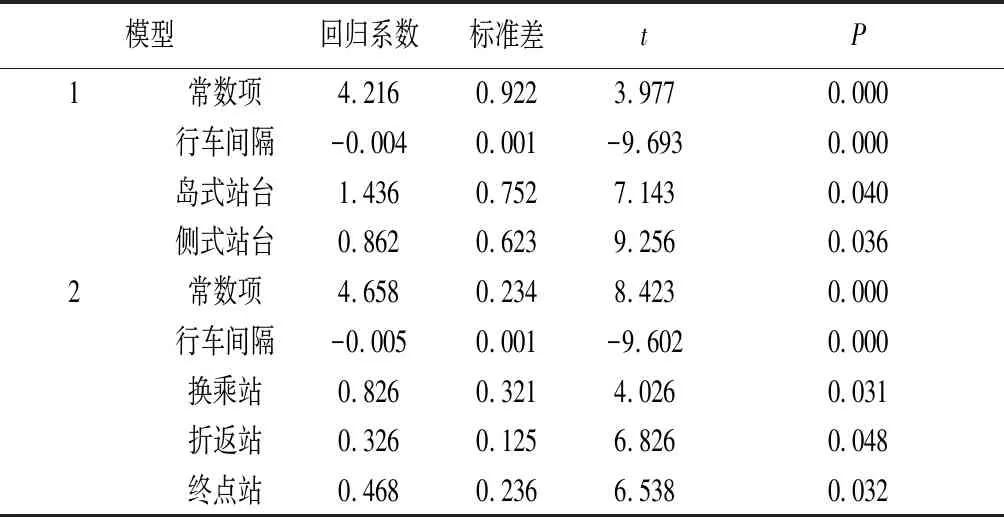
表3 模型回归系数

模型1常数项为4.216，其中行车间隔、岛式站台、侧式站台的回归系数中所对应t值的p值很小，即对于不同的轨道车站形式，行车间隔大小将会使得不同乘客满意度存在明显差异。乘客乘坐轨道交通在岛式站台候车时，回归方程为y=5.2-0.004x，要使乘客乘坐轨道交通时满意度达到“满意(4分)”，则列车开行间隔需控制在5 min以内；乘客在侧式站台候车时，回归方程为y=5.08-0.004x，要使乘客乘坐轨道交通时满意度达到“满意(4分)”；则列车开行间隔需控制在4 min30 s以内；要使乘客满意度达到“一般(3分)”，则岛式和侧式站台行车间隔分别为9 min10 s、8 min40 s。

模型2常数项为4.658，行车间隔、换乘站、折返站、终点站所对应t值的值很小，即对于不同性质的轨道车站，行车间隔大小将会使得不同乘客满意度存在明显差异。轨道交通车站的性质为换乘站时，回归方程为y=5.2-0.005x，要使乘客满意度达到“满意(4分)”，换乘站行车间隔需控制在4 min以内；轨道交通车站的性质为折返站时，回归方程为y=5.95-0.005x，要使乘客满意度达到“满意(4分)”，换乘站行车间隔需控制在6 min30 s以内；轨道交通车站的性质为终点站，回归方程为y=6.4-0.005x，要使乘客满意度达到“满意(4分)”，换乘站行车间隔需控制在8 min以内。

综上计算结果，得到行车间隔与乘客满意度关系表，如表4所示。

表4 行车间隔与乘客满意度值(时间/s)

从轨道车站站台形式看，乘客对于岛式站台可忍受较长行车间隔，侧式站台乘客可忍受的行车间隔相对较短。其中岛式站台行车间隔在550 s以内，乘客均可达到“一般”的状态，侧式站台行车间隔在520 s以内，乘客均可达到“一般”的状态，并且随着行车间隔的缩短乘客的满意度在逐渐提升，说明轨道集团在制定运营组织方案时应综合考虑每线路两种站台形式之间的占比关系。

从轨道车站性质看，乘客对于换乘站得行车间隔要求最高，其次为折返站，最后为终点站，如换乘站乘客达到“满意(4分)”的状态，则该站行车间隔需达到240 s以内，对于行车间隔要求相对较高。究其原因为乘客选择轨道交通出行时默认换乘站客流较大，所以行车间隔较小，加之乘客对服务质量的要求提升，部分乘客认为不同线路列车之间做到无缝换乘才最为合理。折返站和终点站仅该站乘客对于行车间隔要求较高，因站台乘客希望较早乘车便于获得座位，因两类站台在重庆轨道站台中占比为22.94%，所以在制定轨道交通运营组织方案时应适当考虑其影响，避免造成线路总体乘客满意度下降。