地震作用下桥梁墩柱配筋分析

林子力，许芸熙

(云南省交通规划设计研究院有限公司，云南 昆明 650041)

我国是地震多发国家，桥梁在地震力作用下，上部结构因具有足够的强度、刚度和良好的延性，极少遭受直接破坏，而采用钢筋混凝土材料的下部结构往往遭受较大损伤。在桥梁的运营期限内，破坏性的大震发生概率较低，要把桥墩设计成能抵抗罕遇地震，既不经济也无必要。因此，桥梁下部结构的抗震设计目标是：在罕遇地震作用下，通过墩柱的变形来消耗地震作用，但需把墩柱位移控制在一定范围内，确保结构不发生垮塌。

1 工程概况

研究对象为鹤庆至关坡高速公路跨线桥，上部结构为现浇预应力混凝土连续箱梁，采用单箱双室，孔跨布置为20 m+2×26 m+20 m，支座采用盆式橡胶支座，下部结构采用双柱式矩形墩，基础采用桩基础。横断面布置为0.5 m+净8.0 m+0.5 m，设计荷载为公路-I级。桥梁设计基本烈度为VIII度，场地特征周期0.45 s，峰值加速度为0.3 g，场地类型为II类。采用MIDAS Civil 2019软件计算桥梁抗震特性，计算简图见图1，桥梁基本参数见表1。

图1 跨线桥计算简图(桥台未示出)

表1 桥梁下部结构基本参数

2 计算方法

《公路桥梁抗震设计规范》(JTG/T 2231-01-2020)(以下简称《抗震规范》)中把桥梁分为规则和非规则两大类，根据不同的地震作用，针对不同类型桥梁推荐采用反应谱法或者时程分析方法。

2.1 反应谱法

反应谱法是结构抗震设计中广泛采用的一种分析方法，通过采用“地震荷载”的概念，结合地震反应谱求出结构最大的地震响应值。反应谱法的优势在于计算量小、概念简单，对于规则结构通常可简化计算，计算过程主要是把结构的振型方程进行分解，再把反应最大值进行组合，从而得到结构最大反应值。但是，采用反应谱法计算只能得出下部结构弹性计算结果，不能考虑材料和支撑等的非线性影响。进入弹塑性工作范围时，有限元分析中只能结合下部结构轴力-弯矩-曲率(P-M-φ)曲线，通过折减桥墩刚度考虑墩柱进入弹塑性工作后的全桥受力性能，这种简化方法针对下部结构弹塑性工作性能具有较大的局限性。

所以，反应谱计算方法不适用与需要考虑非线性的下部结构。并且，反应谱法计算下部结构受力时只能给出相应阵型的最大地震力，无法精确计算模拟地震作用的全过程。对于高速公路常见的桥梁，相当一部分符合《抗震规范》中所述的“规则桥梁”定义，其地震响应较为简单，因此采用反应谱法分析是适用的。

2.2 时程分析方法

时程分析法是将地震动记录或者人工波作用在结构上，直接进行运动方程的积分，可以得出任意时刻结构的地震响应值。它可以考虑各种复杂非线性因素、桩土相互作用以及分块阻尼等问题。

采用时程分析法虽能较为准确地模拟出下部结构在各个阶段的地震响应，但同样存在几点不足：通常可进行结构时程分析的有限元软件较为复杂、建模工作量大、运算时间长；采用时程分析方法需要设计人员掌握结构非线性、材料非线性、边界非线性等相关知识，从而较为准确地模拟需要进行地震分析的结构；采用时程分析方法计算时通常需要考虑桩-土效应，对于计算采用的土弹簧参数，因其参数较为复杂，主要参数都存在一定的范围、离散性较大，不同土弹簧参数会对结构的动力响应产生较大影响；不同地震波对于计算结果也会产生影响较大，一般情况下地震波可由地震相关部门提供当地的地震波进行分析，但是地震记录不足时则需设计人员结合其它地震波结合相应的频谱特性、有效峰值和持续时间等因素，通过人工选取地震波，《抗震规范》中建议可选取三组地震波采用其中的最大值，或者选取七组地震波通过计算其平均值来综合分析下部结构性能。时程分析法可以对结构的弹塑性状态进行计算分析，是目前进行结构抗震分析较为可靠的方法，有着明显的优势。目前，大多数国家对大跨径、高墩桥梁或者复杂重要的桥梁，因其地震响应和下部结构塑性铰行程机制较为复杂，均建议采用时程分析计算方法。

2.3 本桥采用的分析方法

分析对象为4跨连续梁，桥梁平面位于直线上，单跨最大跨径为26 m，边中跨比为0.77，支座采用盆式橡胶支座；下部结构桥墩采用矩形双柱式墩，最大墩高11.6 m，桥墩计算高宽比适中。地质条件为自地表往下依次为红黏土、黏土岩、中风化灰岩，地质条件良好。依据《抗震规范》表6.1.3，本文研究对象属于规则桥梁，可采用反应谱方法进行计算。

3 参数分析

本桥2#桥墩为制动墩，荷载作用下，所承受水平力远大于非制动墩，故以2#桥墩为研究对象。2#桥墩选用方形截面，截面尺寸为1.4 m×1.4 m，墩高10 m，C35混凝土，墩柱纵向受力钢筋和箍筋均采用HRB400级钢筋，箍筋采用井字复合箍。

采用轴力-弯矩-曲率(P-M-φ)曲线分析桥墩延性时，需结合桥墩配筋定义约束混凝土及钢筋的非线性材料特性，本文中采用Mander(1988)模型定义约束混凝土的本构关系，采用双折线模型定义钢筋的应力应变关系曲线。

3.1 纵筋配筋率的影响

经计算，为保证桥墩在E1地震作用下满足顺桥向强度验算，桥墩顺桥向纵筋数量应不小于42根32 mm直径的HRB400级钢筋，对应纵筋配筋率1.72%，以此为起始每级增加2根32 mm直径钢筋，通过有限元分析计算2#桥墩的抗弯及延性性能，计算结果见图2。

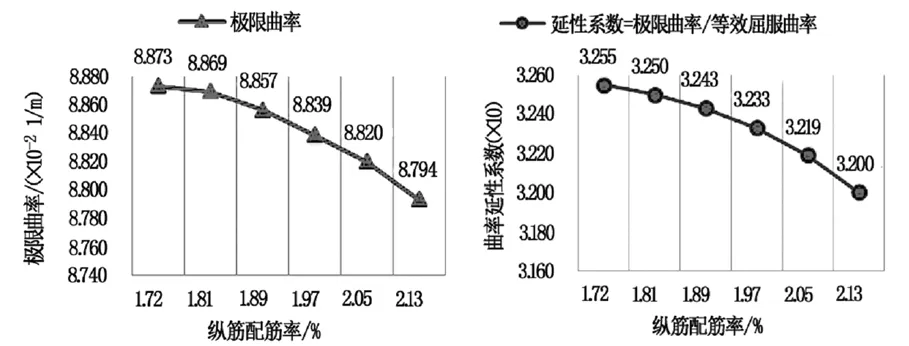
图2 纵筋配筋率对桥墩延性的影响

计算结果表明，在相同受力模式、边界条件约束相同的情况下，通过改变纵向受力钢筋配筋率会影响截面的受力性能，从而改善下部结构的性能和破坏形态。计算结果表明，增大纵向受力钢筋配筋率将减小受压破坏构件的极限曲率，其位移延性也会随之减小。

3.2 配箍率的影响

经计算，为保证桥墩在E1地震作用下满足抗剪强度验算，桥墩箍筋的体积配筋率不应小于0.215%，以此为起始每级增加HRB400级12 mm双肢箍筋环，计算并分析2#桥墩的抗弯及延性性能，计算结果见图3，计算结果显示：随着箍筋配筋率的提高，塑性铰区域截面核心混凝土约束随之提高，混凝土的应变能力随横向约束的增强而增大。计算结果表明，随着箍筋体积配箍率的提高，墩柱延性系数不断增大，墩柱获得更大的延性。

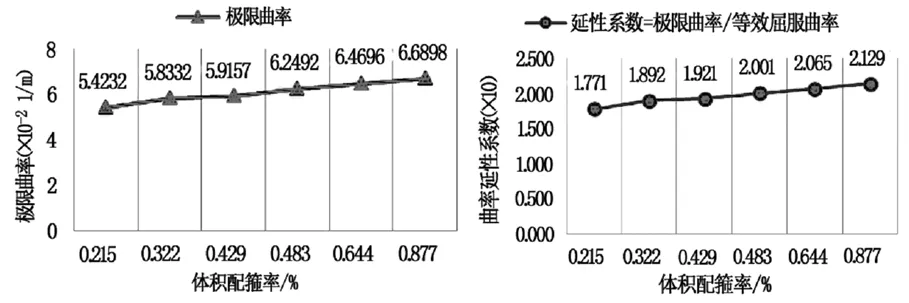
图3 配箍率对桥墩延性的影响

4 结束语

本文从墩柱纵向钢筋配筋率和箍筋体积配箍率入手，计算分析了桥梁墩柱的延性性能，计算结果表明，纵筋配筋率的增大会降低墩柱的延性；箍筋体积配箍率提高的同时，墩柱延性性能也随之增大。所以在桥墩的抗震设计中，在满足E1强度验算的条件下，墩柱的设计应控制纵筋的配筋率，且在满足经济性和施工方便性前提下，可适当增大箍筋的体积配箍率以增加墩柱延性。