基于压电作动器驱动的微操作机构设计与运动控制

2021-10-13马金玉余胜东康升征沈耀辉吴洪涛

农业机械学报 2021年9期

马金玉余胜东康升征沈耀辉潘亮吴洪涛

(1.温州职业技术学院，温州 325035； 2.南京航空航天大学航空学院，南京 210016；3.南京航空航天大学机电学院，南京 210016)

0 引言

作为细胞显微操作的重要研究对象，斑马鱼有70%以上的基因和人类相似[1-2]，同时，依靠其在遗传学上的优势以及高度保守的疾病信号传递轨迹，斑马鱼成为追踪人类疾病信号传递轨迹及生命体高通量药理解析的首选验证生物[3-4]。斑马鱼胚胎细胞尺寸微小[5]，对于像细胞注射等极其精细的显微操作，要求临床人员具备精湛的技艺，能够准确地穿透5 μm左右的细胞膜，在细胞内部实现精密操作[6]。现阶段，以人工为主的手工作业方式严重制约了细胞显微操作技术的进步。

作为智能压电材料，压电作动器(Piezoelectric actuator, PEA)具有位移分辨率高、响应速度快的优点，是实现细胞穿刺的理想动力源[7]。但由于PEA输出位移较小，应用场景严重受限[8]。利用位移放大机构可以使PEA的工作行程获得成倍放大。在微纳操作机构中，柔顺机构具有无传动间隙、无摩擦阻力、兼容性高和易于制造等优势[9]。基于柔顺机构原理设计桥式位移放大机构(Bridge type displacement amplification mechanism，BTDAM)[10]，再利用PEA驱动BTDAM获得大行程的运动。由于PEA也具有无间隙传动的特点[11]，将PEA嵌入到位移放大机构中，两者的机械性能得到高度匹配，在保持运动精度的前提下，扩大了运动范围。

本文以实现对斑马鱼胚胎细胞的显微操作为例，设计一种基于压电作动器驱动的微操作机构以实现对斑马鱼胚胎细胞的穿刺作业。为了提升微操作机构的机械特性，通过动力学理论对微操作机构进行构型优化，在保证纵向刚度和侧向刚度的前提下，完成考察应力分布、强度校核等工作，并获取最大的位移放大倍数。同时，设计与之匹配的非线性鲁棒控制器实现微操作机构的精密运动控制。

1 总体结构设计

传统BTDAM侧向刚度比较低[12]，影响PEA的使用寿命。本文设计图1所示的BTDAM，通过采用平行四边形结构并联式布局，以提高侧向刚度。由有限元仿真可知，对于同样尺寸构成的直梁型柔性铰链，并联式布局的BTDAM的侧向刚度比传统BTDAM提高38.6%以上。

由图1可知，对于并排的一组位移放大机构而言，其构成了平行四边形结构，从而使得位移输出部位获得严格的直线运动效果；所有的16组直梁型柔性铰链都采用一致的几何尺寸，在简化设计过程的同时，保证了整体结构在力学特性上的对称性。

PEA在机构的中心位置处产生推力，使BTDAM发生形变并输出位移。注射针固定于输出位移处。平行四边形布置的柔性铰链用于确保注射针的方向始终保持一致。PEA的位移方向和微进给机构的注射方向垂直。BTDAM的输入沿着X轴方向，注射针的运动方向沿着Y轴方向，如图2所示。PEA的底座通过锁紧机构固定于位移放大机构上。在PEA的顶部设置有表面光滑的球状陶瓷，预紧机构对球状陶瓷施加约20 N的预紧力从而将PEA固定于BTDAM上，并且消除PEA和BTDAM之间的间隙。

2 动力学分析

MIDHA等[13]提出了伪刚体模型，建立了柔顺机构中的“力-变形”准则，成为研究刚柔耦合的重要方法。为此，利用“扭转弹簧+刚性连杆”的关系简化柔性铰链力学模型，从而将柔顺机构复杂的非线性变形过程线性化，这是BTDAM进行数学建模和优化设计的理论支撑[14]。

本文将基于柔顺机构原理，对柔性铰链提出3个模型假设，完成微操作机构的运动学和动力学分析。第1个模型假设，把柔性铰链视为扭簧和其他刚性单元构成的具有单一自由度(Degree of freedom，DOF)的旋转关节[15]，利用伪刚体法完成BTDAM的几何关系分析、瞬时速度分析等。第2个模型假设，将柔性铰链视为具有拉伸刚度和旋转刚度的具有两个DOF的复合运动关节，利用虚功原理求解机构的位移放大倍数。第3个模型假设，在第2个模型假设的基础上，考虑柔性铰链的局部尺寸，将其视为具备3个DOF的复合运动关节，利用矩阵方法求解放大倍数。

由于该机构是中心对称的结构，为了简化求解过程，以四分之一模型作为研究对象，图3为四分之一BTDAM的运动简图。其中，Fx、Δx分别是施加于四分之一机构上的输入作用力和输入位移，Δy是机构的输出位移。因此，对于完整的机构而言，输入作用力、输入位移和输出位移分别是4Fx、2Δx、2Δy。

2.1 柔性铰链单自由度建模假设

将柔性铰链视为单一DOF的转动关节，转轴为柔性铰链的中心部位，其余部分为刚性体。

由图3可知，PEA产生水平方向上的输入位移Δx，引起柔性铰链发生变形，得到BTDAM的输出位移Δy，同时，将上连杆AB或者下连杆CD的倾角由α转变为α*，可得

lacosα+Δx=lacosα*

(1)

式中la——上连杆AB或者下连杆CD的长度

消除α*，可得

(Δy)2-2lasinαΔy+(Δx)2+2lacosαΔx=0

(2)

整理式(2)，可以求出输出位移Δy为

(3)

因此，可以求出输出机构的位移放大倍数C1为

(4)

从式(4)可以看出，对于指定的机构而言，la和α是给定的，因此，位移放大倍数只表现为与输入位移Δx相关的单变量函数。

从式(1)能够看出，机构的最大输出位移，即Δy极限值发生在α*→0时，则Δymax→lasinα。

2.2 柔性铰链二自由度建模假设

假设柔性铰链具有拉伸刚度Kt和旋转刚度Kr，其余部位为刚性体。对其中的一条连杆，如连杆AB，其受力状态如图4所示。规定Fx=FAx=FBx，在点A建立力矩方程，可得

Fxlasinα=2Mr=2KrΔα

(5)

其中，力矩Mr由旋转刚度Kr作用产生，并使上连杆AB发生Δα的转角。

在点A建立力方程为

(6)

式中 Δl——由拉伸刚度Kt引起的轴向位移

基于虚功原理，构建能量方程为

FxΔx=FlΔl+2MrΔα

(7)

结合式(5)～(7)，可得

FxΔx=Kt(Δl)2+2Kt(Δα)2

(8)

进而构建输入位移与输入作用力之间的关系

(9)

对等式ly=lasinα关于时间求导，得

Δy=lacosαΔα

(10)

可以得到位移放大倍数为

(11)

对于整体机构而言，其输入刚度为

(12)

2.3 柔性铰链变截面刚柔耦合建模

考虑柔性铰链的详细尺寸，并结合伪刚体法和Euler-Bernoulli柔性梁理论建立BTDAM的精确静力学模型，再根据Lagrange方法建立机构的动力学方程[16]，求出机构的自然频率。

如图5a、5b所示，假设机构的输出位移Δy主要来源于上连杆AB和下连杆CD的弯曲变形。在点A建立力矩方程，可得

Fxly-2Mr=0

(13)

柔性铰链的变截面布局如图5c所示，将上连杆AB或者下连杆CD分成3段，其高度为

h1,2(dx)=t(dx∈[0,a]∪[a+b,2a+b])

(14)

h3(dx)=c(dx∈(a,a+b))

(15)

3段的扭矩分别为

M1(dx)=Mr(dx∈[0,a])

(16)

(17)

M3(dx)=-Mr(dx∈[a+b,2a+b])

(18)

根据Euler-Bernoulli[17]柔性梁理论建立3段柔性铰链的角度变形量为

(19)

(20)

(21)

式中Pi——常数，i=1，2，3

E——弹性模量w——任意横截面扰度

对角度变形量做积分运算，可得3段柔性铰链的位移。

机构的输入位移Δx和输入作用力Fx相关联。从四分之一模型可以看出，输入位移Δx来自于主体OA段、上连杆AB和下连杆CD的变形。对上连杆AB和下连杆CD处的作用力进行平移合并，得

(22)

参照图5b所示的坐标系，坐标x处的力矩为

M(x)=Fx(2x-l1-l2+ly)

(23)

对应的角度变形量为

(24)

式中P4——常数

对式(24)做积分运算，得位移变形量为

(25)

因此，在点A处的位移变形量为

(26)

如图6所示，上连杆AB或者下连杆CD由于拉伸变形而产生的变形量为ΔL=2Fx/Kt，其沿x轴的位移量Δx2，沿y轴的位移量Δy分别为

Δx2=(La+ΔL)cosα*-Lacosα

(27)

Δy=Lasinα-(La+ΔL)sinα*

(28)

其中

式中La——连杆近似长度

消去α*后可以求得Δx2为

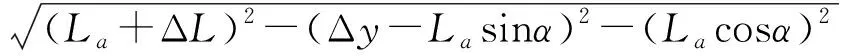
(29)

至此，可以求得机构位移放大倍数为

(30)

机构输入刚度为

(31)

至此，通过上述3个模型假设，建立了机构的位移放大倍数和输入刚度。

2.4 基于Lagrange方法的自然频率分析

对于BTDAM而言，其输入位移为q=2Δx，机构动能和势能分别为

(32)

(33)

将式(32)、(33)代入到Lagrange方程[18]中

(34)

式(34)可以整理为

(35)

其中

(36)

(37)

式中M——等效质量K——刚度系数

因此，机构自然频率为

(38)

3 机构几何优化

基于建立的BTDAM的数学模型，进一步通过数值计算方法完成机构的几何优化。为了提高优化效率，将通过智能优化算法，以位移放大倍数的最大值为优化目标，在保证自然频率等相关边界条件的约束下确定机构的几何尺寸。在ANSYS Workbench[19]平台上对结构尺寸进行计算机有限元优化。

3.1 基于差分进化算法的几何优化

利用智能优化算法完成几何结构的数值优化计算[20]。基于群体随机并行搜索策略而形成的差分进化算法(DE)[21]，模拟自然界中各种群间既合作又竞争的生存模式，计算过程比传统的遗传算法更简化、高效。DE算法步骤为：

(1)种群初始化：初始种群的选取应来自于整个解空间。

(2)差分变异：目的在于增强算法的全局搜索能力，可以通过DE/rand/1策略，进而得到解空间的最优值。

(3)交叉操作：交叉操作位于差分变异的后续环节，通过将交叉概率CR设置为随适应度函数而变化的动态变量，在确保全局搜索能力的前提下，也可兼顾局部搜索能力，是算法的核心步骤。

(4)选择操作：依据贪婪策略淘汰掉适应度大的个体。

图7为DE算法流程图。

由于变截面刚柔耦合建模过程更精细化地体现了柔性铰链几何尺寸，考虑到优化的核心为柔性铰链几何尺寸。因此，基于变截面刚柔耦合建模过程而建立的位移放大倍数和输入刚度将被应用于优化过程。另外，机构的自然频率也将被应用于优化过程。

为了获取一个结构紧凑的机械结构，柔性铰链的4个参数(a、b、c、t)(图1)作为主要设计变量，并为其设置较为合理的取值范围。因此，它将演变成一个在多约束条件下的单目标优化问题。优化计算需在表1、2所示的边界条件下进行。

表1 约束条件和优化目标Tab.1 Constraints and optimization objectives

表2 柔性铰链设计变量的取值范围Tab.2 Size range of flexure hinge mm

经过DE优化后，获得柔性铰链的尺寸为：a=3.125 2 mm、b=6.460 8 mm、c=4.355 2 mm、t=0.290 5 mm，自然频率为201.68 Hz。

由于BTDAM的结构精细复杂，3D打印技术为其制备提供了便捷的途径。材料为由光敏树脂与聚丙烯构成的混合物，几何精度达到±0.015 mm。材料性能为密度905 kg/m3、杨氏模量1.5×109Pa、泊松比0.41。

3.2 基于有限元仿真技术的几何优化

通过对模型进行必要的简化后，在ANSYS Workbench 19.0软件中完成几何体构建，对设计变量进行参数化设置[22]。对零件进行多次slice划分后，再合并成一体，然后进行网格划分，得到95 569个节点和19 524个六面体单元。为模型配置载荷并设置约束条件，2个输入位移量均为5 μm。先进行静力学分析，再进行模态分析，将零件的固有频率和主要设计变量进行关联。

在Design Xplorer/VT模块中利用GA(Genetic algorithm)算法完成参数的优化迭代。优化模块自动选择并排列最佳结果。表3为优化结果。

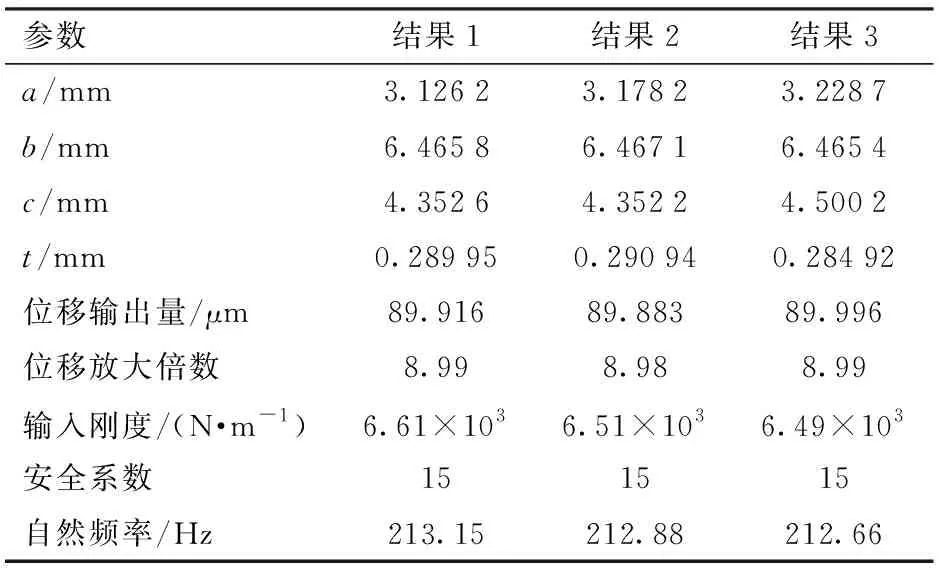
表3 优化结果Tab.3 Optimization results

由于所采用的PEA刚度为2.0×108N/m，比3种优化结果的输入刚度大5个数量级。因此，在设计过程中忽略了执行机构刚度。

由表3可知，由于3个结果的数值较为接近。同时，一并考虑GA优化的结果，显然结果1具有最高的固有频率。因此，选择这组参数应用于物理样机的制作。

3.3 六阶模态分析及优化结果的验证

为了验证有限元优化设计的结果，通过ANSYS Workbench 19.0软件对结构进行仿真分析。静态分析结果反映了结构的应变状态和应力分布，由图8可知，当向两端各施加5 μm位移时机构的最大输出位移为89.916 μm；由图9可知，当向两边各施加位移10 μm时机构的最大应力为1.014 6×106Pa。对结构进行模态仿真分析，一阶共振频率213 Hz，这个频率对于细胞穿刺已经足够高。

BTDAM的六阶固有频率如表4所示。与DE优化相比，其自然频率提高了5.39%，可以证明柔性铰链的数学模型和优化过程具有可靠的精度，并且两种研究途径基本实现了相互验证。

表4 BTDAM的前6阶模态Tab.4 List of the first six modes of BTDAM

4 性能实验

借助于BTDAM的位移放大功能，扩大了PEA的运动范围，使微操作机构获得了180 μm的行程；但同时也恶化了PEA的迟滞非线性效应。本文提出一种基于干扰观测器的PID控制策略，将外部干扰、迟滞非线性效应等不确定因素均视为未知项，利用干扰观测器实现对未知项的实时观测和在线补偿，从而提高系统动态性能和刚度；并结合PID控制消除静态误差，最终达到提高系统综合控制品质的目的。

4.1 控制器设计

利用牛顿定律和Bouc-Wen模型构建微操作机构的迟滞动力学模型[23-24]，方程为

(39)

(40)

u——激励电压

b——阻尼系数k——刚度系数

d——电压系数h——迟滞项

ζ1、ζ2、ζ3——迟滞项系数τd——扰动项

对系统的迟滞动力学模型进行适当简化，即

(41)

观测器定义为

(42)

(43)

设计Lyapunov函数

(44)

(45)

假设未知项为连续变化的函数，且其一阶导数有界，当k1为较大数值时，有

(46)

将式(42)～(44)代入式(45)，得

(47)

通过借助于观测器实现对未知项Δ的实时估计和在线补偿，并将其和PID项相结合，构成基于干扰观测器的PID控制策略，即

(48)

式中Kp——比例项系数

Ki——积分项系数

Kd——微分项系数

e——位移误差

4.2 位移跟踪实验

基于xPC半物理仿真环境构建微操作机构的运动控制实验系统。采用Pst120/7/20VS12型PEA和E00.6型电压放大器。PEA位移信号由LK-H020型激光位移传感器采集，其测量精度为0.02 μm。

流程框图如图10所示，控制算法运行于宿主机上，经过编译后下载到目标机中。目标机输出的数字信号经数模转变，由电压放大器进行放大，然后驱动PEA运动。激光位移传感器采集的位移信号，经过模数转变后，再经过低通滤波器，输入到目标机中。半物理仿真实验平台如图11所示。

利用试错法对控制器的参数进行调整，并且综合考量抖振程度、均方根误差(Root mean square error，RMSE)和最大误差(Maximum error，ME)[25]，选择的参数为Kp=5×107、Ki=8×107、Kd=100、k1=5×105、k2=50。

为了使仿真结果更具代表性，选择幅值为100 μm、周期为2 s的正弦信号作为期望轨迹，其轨迹曲线如图12所示。

由图13可看出，所提控制器和PID控制器都能实现对正弦信号的轨迹跟踪。两个控制器产生的位移误差曲线随正弦曲线发生同步波动，但所提控制器产生的误差波动远小于PID控制器的误差。对位移误差曲线进行量化分析可得，所提控制器的RMSE为0.071 μm、ME为0.128 μm；PID控制器的RMSE为0.322 μm、ME为0.506 μm。可见所提控制器具有更优的运动跟踪精度。

如图14所示控制律曲线表示控制器中PID项、观测器项和总控制律的构成与占比。观测器的主要作用在于实现对未知项的估计，因此，也间接反映了未知项在被控系统中所占的比例。对传统PID控制而言，未知项所占比例越高，对运动控制精度的影响将越大。所提控制器利用观测器对未知项进行在线补偿，在总的控制律构成中，观测器项承担了大部分的控制输出，能够大大减轻PID项所承受的负担。

从图14还可看出，PID项、观测器项和总控制律这三者基本呈现同步波动的状态，从另外一个角度验证了观测器设计的正确性，说明了观测器项能够积极补偿PID项的输出，起到了正相关作用。

此外，观测器项的输出曲线呈现光滑变化，而PID项的输出曲线表现出一定幅度的抖振。因为，在观测器的设计中，通过积分实现未知项的估计，噪声信号经过积分运算后会趋于平滑。而PID项中的微分项对噪声比较敏感，噪声会引发PID项的输出发生抖振。

面对存在较大比例未知项的被控对象，基于干扰观测器的PID控制策略相比于传统的PID控制而言，更适合应用于微操作机构的运动控制。