波利亚在函数最后集上的贡献

王全来

(天津师范大学计算机与信息工程学院,天津 300387)

1 引言

多项式以及整函数零点问题经常出现于数学、物理学和经济学等学科中.该问题在柯西、傅里叶、波利亚等人工作的影响下,关于多项式以及整函数零点的研究一直是数学学科的经典课题之一.多项式的零点定理一般不能自然地推广到整函数上去,特别是有微分运算的定理,对此波利亚做出了奠基性的工作.他深入研究了一个函数在微分运算下的零点行为,得到了许多深刻结果,函数的最后集理论即是其中之一,其思想和方法影响至今.函数的最后集理论散见于一些数学理论著作中.对于波利亚的最后集工作,阿兰德森(G.L.Alexanderson)在2000年的著作中只是简单提及,缺乏系统研究[1].除此之外,国内外尚未见到其它研究文献.鉴于此,本文以原始文献(挖掘了一些鲜为人知的文献,如马尔科夫 (A.A.Markoff)、费耶(E.Feyer)等人的工作)为依据,系统梳理了波利亚在函数最后集上的工作,借此探讨了函数最后集理论的发展脉络,以补现有文献的不足.

2 最后集提出的背景

2.1 波利亚之前一些学者的相关工作

多项式零点理论中一个重要组成部分是对多项式及其导数零点关系的研究,例如早在1816年,高斯在数学笔记中就对多项式导数的零点给出了物理解释.1874年,拉卡斯(F.Lucas)阐述并证明了高斯-拉卡斯定理:一个多项式导数的零点包含在该多项式零点的凸包中.在1901年,格瑞斯(J.H.Grace)在5页篇幅的论文中获得了一个奇特的非极性定理.若f(z)为一个多项式,

f(a)=f(b)=0,

一个无穷级数a0+a1z+a2z2+···在z的整个有限平面内收敛,在一定意义上是多项式a0+a1z+a2z2+···+anzn的一般化,称为整函数.然而把关于多项式零点的一些定理毫无限制地用于整函数的努力失败.例如若一个多项式只有实根,则其导数也只有实根,但对整函数而言不一定成立.波莱尔在“整函数课程”(1900)中对此有详细介绍.这个理论的主要问题之一是寻找实函数的零点和其导数零点的关系.在这个方向,拉盖尔在19世纪80年代早期首先考察.自从那之后很少有进步获得,直到波利亚才获得了一些有意义的推广.

值得一提的是,在此期间,奥兰德(M.Ålander)的工作对波利亚有重要影响.他的工作主要是对函数连续阶导数的零点问题进行了深入研究,其发表的3篇论文,“整函数导数的零点迁移”(1914),“实整函数导数的例外根”(1916),“有理函数和其它亚纯函数的导数的零点”(1920),主要结果和型是2,3,4,5的整函数及有理函数有关,阐述了一些值得注意的观点和猜想及一些启发性研究的例子[4].波利亚不仅回答了奥兰德提出的一些问题,而且在此基础上进一步研究和思考.

2.2 波利亚与之有关的早期工作

波利亚首先涉及这方面的工作,始于他和林德瓦特(E.Lindwart)在“论多项式序列的收敛和零点分布之间的关系”(1913)中研究多项式序列零点分布问题.在该文中,他们指出,若级数a0+a1x+a2x2+···在|x|<1内收敛,且系数满足a0>a1>a2>···>0,则收敛圆的整个圆周上的点属于零点的聚集.詹逖生(R.Jentzsch)在1914年、1918年证明,若Pn(z)=a0+a1z+a2z2+···+anzn表示幂级数a0+a1z+a2z2+···的前n项和,则圆周|z|=R的每个点为Pn(z)的零点的聚点,其中R为有限数[5].

波利亚在“关于整函数的一个问题”(1914)和“整函数理论注释”(1915)中指出,若一个超越实整函数和其二阶导数的零点是实的,则所有导数的零点为实的.在上述文章的基础上,波利亚在“某超越整函数零点的几何释义”(1920)中对指数多项式零点分布从几何角度研究,给出了一般性定理,但没有证明.详细和进一步的结果出现在其学生施温格尔(E.Schwengeler)的博士论文中[6].波利亚的这个工作开创了指数类型的整函数零点分布的现代理论.中国学者庄圻泰,李文清等在这方面涉及了一些工作.

在这篇文章中,波利亚给出3个重要定理.其中如下定理奠定了波利亚其后提出函数最后集的思想基础.

设超越整函数

为复平面内互不相同的点,P1(z),P2(z),···,Pm(z)为多项式,m大于 1.a1,a2,···,am的共轭为b1,b2,···,bm,µ为包含a1,a2,···,am的最小凸多边形,µ∗为包含b1,b2,···,bm的最小凸多边形,则F(z)的零点集中趋于l条不同的射线,多边形µ∗的外法线是平行的,其中l是与这些点有关的射线,且l≤m.

值得一提的是,该文中的另一定理给出了在多边形的每条边上的零点数的估计值,引起了其他学者的注意,如杜邦 (E.Dubon)在 2015年,何透康斯 (J.Heittokangas)在2019年的研究[7]等.

3 波利亚在最后集上的重要工作

波利亚在函数最后集上的工作主要涉及的论文有6篇,分别是“连续阶导数的零点”(1922),“詹森的代数函数理论研究”(1927),“与傅里叶关于超越方程有关的一些问题”(1930),“某类整函数几乎所有导数的零点的实性”(1937),“一个函数的导数的零点和其解析性”(1943),“连续阶导数的零点:一个例子”(1976).波利亚在1922年的论文中提出了最后集思想,但没有给出最后集的名字:随后的四篇论文,波利亚对特殊类的整函数的最后集进行了研究:波利亚在1943年正式给出分析学定义和命名.

3.1 最后集思想的提出 —1922年文章的分析

波利亚在“连续阶导数的零点”(1922)中正式提出了函数最后集的思想.该文分为四部分.在第一部分绪论中,波利亚指出研究函数的n阶导数零点分布问题是本文的中心,并给出了4个重要定理,从几何上进行了解释,没有给出严格证明.

定理 3.1设R(z)为一个有理分式函数,R(n)(z)的非实零点数随着n增加,除下面两种例外情况.(1)R(z)在平面内只有一个极点;(2)R(z)在平面内有两个关于实轴对称的极点.该定理回答了由奥兰德在1920年的论文中提出的问题.

定理 3.2设P(z),Q(z)为多项式,Q(0)=0,G(z)=P(z)eQ(z).G(n)(z)的非实零点数随着n增加,除下面两种例外情况.(1)G(z)的次数为1;(2)G(z)的次数为2,Q(z)=bz−cz2,b为实数,c大于0.该定理改进了波利亚在“关于整函数的一个问题”和“整函数理论注释”中的主要结果.

定理 3.3设F(z)为亚纯函数,研究由其各阶导数零点构成的可数集合,这个集合的聚集只依赖于F(z)的极点位置.点z属于聚集当且仅当z与F(z)的两个最近的极点等距.

该定理给出了一个漂亮结果,一个亚纯函数的全部导数的零点的聚集由多边形构成,其顶点是与两个最近的极点等距的点.

定理3.4设P(z),Q(z)为多项式,

G(z)的各阶导数零点集的聚点只依赖于次数q,b和b1.由点z=−b1q−b出发的q条射线把平面分割成q个相等的角域,这些射线可以理解成与方程bzq+1=0的q个根形成的向量平行.

该定理由麦克兰尼 (G.R.MacLane)在 1955年推广到P(z)为标准积的情况[8].麦克劳德 (R.Mcleod)在 1959年利用筛点法进一步一般化[9].该法由海曼(W.K.Hayman)在“斯特灵公式的一般化”(1956)中提出.

给出定理3.1,定理3.2之后,波利亚指出,“我们的注意力不要仅放在这些特例上,而更应放在方法上,而这种方法就是几何方法”,“在定理3.3中提到的聚点集合为一个纯粹的几何想象的奇特的集合,将有一个详尽的描述”.波利亚给出如下解释:设a为指定亚纯函数F(z)的一个极点,z为平面内的点,与F(z)的其它极点相比,更靠近a.建立a的活动域,当a和b为F(z)的两个不同极点时,活动域有共同的边界点,位于a和b的垂直平分线上,a的活动域为一个凸多边形的内点,并最终趋于无穷.

惠特克(J.M.Whittaker)受波利亚关于最后集几何思想的影响,在“插值函数理论”(1935)的第3章中专设一节以“一个亚纯函数导数零点无穷行为的波利亚定理”为标题讨论了波利亚的最后集定理,他称为波利亚郡定理,并给出了十分具有启发性的几何解释.f(z)的一个极点λ的郡将由平面内所有点z构成,与f(z)的其它极点相比更接近于λ,则一个亚纯函数的最后集由其极点的郡的边界构成[10].海曼在“亚纯函数”(1964)中给出该定理的证明.

由定理3.3知,亚纯函数及其各阶导数的零点构成集合的聚集,和边界线上的全部点的集合相等,亚纯函数的不同极点的活动域是不同的.这个区域由极点控制,和这样的点的集合相等,在其中亚纯函数可以展成一个幂级数,收敛边界上有唯一奇点.平面内只有这样的点才能是一个亚纯函数连续阶导数零点的聚点.当亚纯函数只有一个极点时,连续阶导数的零点无聚点.若亚纯函数只有一个极点,则该函数的最后集是空的,唯一极点对于该函数的连续阶导数可产生无零点的区域.这样的无零点区域的渐近大小在萧氏(J.K.Shaw)和普拉瑟(C.Prather)1982年的论文中得到[11].

马尔科夫在1912年曾证明,有理函数(1+z2)−1的n阶导数有n个实根,由此可得到e−z2的连续阶导数的零点,且与实轴上的每个点无限接近[12].由定理3.3,定理3.4知,在上面的研究中,n阶导数的零点集随着n趋于一个极限位置.波利亚指出,“在某种意义下,我将在后面给出准确定义.这个极限位置和全部零点的聚点集相等”.

第二部分(亚纯函数):在这一部分中,波利亚讨论了平面内的3类点,借以把亚纯函数的各阶导数的零点集分为3类,给出了定理3.3的两个补充定理.

补充定理3.1:若F(z)为亚纯函数,其n阶导数的零点集趋于一个固定的极限位置,一个点属于这个极限位置当且仅当该点位于两个最近的极点的平分线上.

补充定理3.2:若F(z)为亚纯函数,其n阶导数的a-点集合趋于一个固定极限位置,这个极限位置和由n阶导数的a-点构成的可数点集的聚点集合相等.

第三部分(具有有限多个零点的有限型的整函数):在这一部分,波利亚依据凸多边形理论,采用几何语言对定理3.4进行阐述和说明,用到了柯西中值定理.

第四部分(例外情况的讨论):对定理3.1,定理3.2中给出的例外情况进行讨论.设R(z)为有理函数,R(n)(z)=F(z−1).通过R(n)(z)的零点行为在z=∞处的情况可得到F(z−1)的零点行为,这个函数的零点分布与最小凸多边形理论研究有关.值得一提的是,庞加莱在1895年,费耶在1919年都对此有所论及[13],并对波利亚有一定影响.

在文末,波利亚提出希望读者继续对第四部分的问题进行研究,得到了一些学者的响应,如包斯(R.P.Boas)、萧氏、普拉瑟等人获得了一些深刻的结果.

3.2 实整函数的最后集研究

波利亚在“詹森的代数函数理论研究”(1927)中阐述但未证的一个断言:“若一个实整函数f(z)的阶小于,f(z)只有有限多个虚根,则其导数从某项开始无虚根”.他在1930年的文章中给出该论断的证明,并提出傅里叶-波利亚猜想.奥兰德在1930年也独立证明了该论断,并给出一个非常惊人的定理,“存在任意阶的整函数,在复平面的每个点的邻域内导数为 0”[14].以此为据,利用波利亚 1922年文章的思想,威曼(A.Wiman)在1930年给出如下定理:存在一个整函数ezf(z),f(z)为型是0的整函数,其导数的零点的聚点有两种可能或是整个实轴或为无穷[15].

威曼在奥兰德,波利亚等人的影响下,在1937年推广了他们的定理,证明阶小于1时结论也成立[16].同年,波利亚在看到威曼的论文手稿后,证明对于一个实整函数,且只有有限多个非负实根,只要阶小于,则其最后集为实轴子集.他也猜想可以由2代替,由柯夫(T.Craven)、科尔达斯(G.Csordas)、史密斯(W.Smith)在1987年证明[17].普拉瑟在1986年证明,当用更一般的微分算子代替微分运算时波利亚提出的的结论也成立[18].

威曼在1937年的论文中曾指出,仅通过函数非实零点的位置可得到一个确定的区域,其n阶导数的全部非实零点包含在内.波利亚在1937年进一步指出,若函数的每个非实零点α+iβ满足|β|<1,则仅通过函数的非实零点的位置确定一个n0,当n>n0时,函数的n阶导数的全部例外零点和全部非实零点都位于圆内.他在该文中深入探讨了函数的可疑圆和自由圆问题.令f(z)为超越整函数,若rk是以坐标原点为圆心的最大圆半径,在其中f(k)(z)无零点.包斯、雷迪(R.Reddy)在1973年指出,若f(z)为阶至多是2的有限型的整函数,则在平面内任意处存在任意大圆,在其中无穷多个f(k)(z)无零点[19].在包斯和雷迪论文之后,雷迪在1974年考察了对D算子的无零点圆问题,证明了对于导数出现的许多结果为该算子一般理论的特例[20].对于阶高于2,该定理不再有效.在这方面有一个假设为包斯猜想:若ρ>2,则存在阶是ρ的整函数f(z)使得对某个正数A,半径为A的任意圆,无论在平面何处,总含f(n)(z)的一个零点.普拉瑟、萧氏在1983年对此也有探讨[21].

3.3 最后集的分析学定义及其命名 — 1943年文章的分析

波利亚在1922年的论文中发现了函数的极点分布和最后集之间的非常有趣的联系.波利亚在“一个函数的导数的零点和其解析性”(1943)中,以这个问题开始,“当n很大时,f(z)的第n阶导数的零点行为如何?这些行为依赖于f(z)的解析性质吗?f(z)的连续阶导数的零点有确定趋势吗?若有,我们能找到这种趋势吗?”

波利亚在该文第二部分给出了几个关键性的定义,其中之一为函数的最后集,最后集的名字首次出现.一般来讲,一个极点的邻域是一个开的凸集,其边界由折线构成.波利亚定义了一个集合称为函数f(z):C→C的最后集D,由f(z)的全部导数的零点集的聚点构成.

在第三部分 (亚纯函数),波利亚开篇指出:设f(z)为亚纯函数,其极点作为关于f(n)(z)的零点排斥的中心.一个亚纯函数的最后集不含任何极点区域内部的点,但含所有在两个或多个极点区域的共同边界的点.值得注意的是最后集完全由f(z)的极点分布确定,不依赖于极点的阶及留数.

在第四部分(具有一个本性奇点的函数),波利亚考虑了点z=0为有限奇点情况.若z=0为一个极点,整个平面为其区域,则f(n)(z)的零点趋于无穷,无极限点,最后集为空集.但z=0若为本性奇点,则情况不同.f(n)(z)的零点的运动趋势不定,只依赖于奇点位置不再正确,例如f(z)=z−1e−z−1,f(n)(z)的零点为正实数,最后集为正半轴.波利亚没有给出该断言的证明.若z变为zeiα,为固定实数,0<α<2π,则f(z)的奇点为原点,但f(n)(z)的零点沿来自于该奇点的另一条射线趋于稠密,最后集改变位置.在波利亚该例的影响下,埃德雷(A.Edrei)在1987年研究了的最后集问题,其中g(z)为只有实根的阿达玛积[22].克拉尼(J.G.Clunie)、埃德雷在1991年利用类似于埃德雷的推理把函数g(z)推广为满足一定条件的超越整函数的情况,一般化了上文中的有关结果[23].

第五部分 (整函数),在该部分中,波利亚讨论了n趋于无穷时,整函数的导数f(n)(z)的零点趋势,这种趋势主要依赖于f(z)的阶.波利亚并断言“若一个实整函数f(z)的阶比1大,则f(n)(z)的零点随着n的增加集中趋于无穷.若一个实整函数f(z)的阶比1小,则f(n)(z)的零点随着n的增加而分散趋于无穷”.要注意的是,波利亚描述的上述现象是非常一般的和定性的.

设λ表示整函数f(z)的阶,则

其中rn表示f(n)(z)的零点最近于原点的距离,Nn表示f(n)(z)在|z|≤1内的零点数.

当λ<1时,奥兰德在 1914年给出 (1)式,更多更准确的关系由贡察夫 (W.Gontcharff)在“解析函数连续阶导数的研究”(1930)中给出[24],贡察夫的研究思路由竹田 (S.Takenata)、卡克、勋伯格 (I.J.Schoenberg)等人继承和发展[25].当f(z)为有限阶λ>0,α>λ时,存在无穷增加的k的序列使.波利亚在该文提出λ>1.埃尔多斯 (P.Erdös)、仁伊 (A.Rényi)在 1956年给出λ>1的第一个证明,在其中奥兰德的结果被错误地引述为λ>1[26].当λ=1,f(z)为指数类型τ时,更准确的结果是rk≥c(τ),c(τ)为一常数,由竹田在1932年给出[27].该结果由巴克霍尔茨(D.Buckholtz)、弗让柯(J.L.Frank)在“惠特克常数”(1971)中进一步研究[28].包斯在1940年引入了一个与之相关但不同于rn的量,后由列文森(N.Levinson)在1941年发展.令Sn表示圆心在z=0处的最大圆半径,在其内f(z)是正则函数,f(n−1)(z)是单值的,则有

(2)式是波利亚首次提出的.在该文注脚处指出,若λ≤1,则最后集可能为空集,并且可以构造任意给定阶的整函数,其最后集由一个点构成:若λ>1,最后集一定含一个点吗?该问题由埃德雷和麦克兰尼在1956年的论文中给出详细解答[29].

波利亚在该部分提到“阶为1的整函数f(z)=sinz,微分运算不改变其导数零点分布的稠密性”的例子引起了一些学者的关注.普拉瑟在1984年发表了一个证明,肯定了该假设定理[30],但其证明存在一处错误.实际上,该错误是严重的,饶欧(M.Rao)、申(L.C.Shen)在1987年构造了一个反例,否证了上面的假设定理.他们指出,存在指数类型的实整函数,在实轴上有界,使得整个实轴属于它的最后集.并给出如下猜想:令f(z)为一个阶为1的实整函数,指数类型为ρ,在实轴上有界,则f(z)的最后集在实轴上为一个等间隔的无穷集[31].应当指出,该定理与波利亚的阐述不矛盾.对于波利亚而言,只说f(n)(z)的零点分布的稠密度基本不变.

申在1987年继续探讨,给出下面猜想:令f(z)为指数类型的,阶是1的实整函数,在实轴上有界,则f(z)的最后集为一个等间距的无穷集,n为整数,τ为f(z)的型.在该文中,申证明了一个稍弱的猜想[32].

第六部分(实整函数),一个实整函数的零点集关于实轴对称,实轴对f(n)(z)的复根起着重要影响.当f(z)的阶小于2时,吸引这些零点,当阶大于2时排斥这些零点.波利亚给出了两个猜想:

A:若实整函数f(z)的阶小于2,且只有有限个复根,则其各阶导数,从某一阶开始不再有复根.

B:若实整函数f(z)的阶大于2，且只有有限个复根,则n趋于无穷时,f(n)(z)的复根数趋于无穷.

猜想A由威曼和波利亚独立发现,现称波利亚 -威曼猜想.在1987年,柯夫,科尔达斯,史密斯在f(z)是0类或1类时证明了波利亚-威曼猜想.柯姆(Y.O.Kim)在1990年通过完善他们的证明在一般情况下证明了该猜想[33].

猜想B可由例子e−z2k和e−eez说明.e−z2k的最后集由k条通过原点的直线构成,把平面分成2k个等角.e−eez的最后集由无穷条平行线组成,平面由宽度为2π的直线分割,该问题由波利亚提出,由斯泽古证明,但未出版.若k≥2,则这两个函数的最后集包含整个实轴,而且包含实轴外的点.海勒斯坦(S.Hellerstein)、杨(C.C.Yang)在1970年利用土姆-克拉尼定理部分肯定猜想B[34].埃德雷在1980年提到,波利亚在给埃德雷的一封信中询问他是否能给出这个事实的证明.由于斯泽古在他的笔记中没有找到该证明的记载,这是一个无法补救的损失.波利亚和斯泽古感到都不能再重新研究这个问题了.在此情况下,埃德雷研究了e−ez的最后集,指出由直线y=2πl,(l为整数)组成,并给出证明[35].埃德雷在研究该问题时看到了普拉瑟当时未出版的“一些整函数连续阶导数的零点”的手稿,对其有一定启示.普拉瑟在该文中研究了该函数的幂级数展开,指出该级数系数的97%以上不为0,并猜想当n充分大时,系数不为0[36].埃德雷在该文中给出了该猜想的一些相关信息.该例由雷门(J.W.Layman)和普拉瑟在1983年通过研究贝尔数进一步探讨[37].格斯纳(R.Gethner)在其1982年的博士论文中对某类函数证明了猜想B[38].

伯格威勒 (W.Bergweiler)、叶列缅科 (A.Eremenko)在 2006年涉及猜想B.令f(z)为有限阶的实整函数,有有限多个非实根,f(z)不是一个实多项式和类LP中的函数之积,则f(n)(z)的非实根数N(f(n)(z))满足[39].对于无穷阶的实整函数,具有有限个非实根,兰利(J.Langley)同年证明

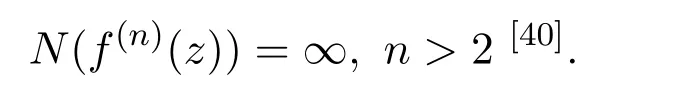
第七部分(关于实整函数的其他开放问题),波利亚提出了猜想C:若一个阶比1大的实整函数对变量的实值保持有界,则最后集包含整个实轴.埃德雷在1956年对该猜想有所涉及,并给出一个重要结果.令f(z)为实超越整函数,满足形如

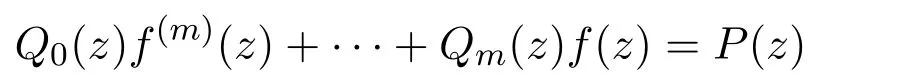
的微分方程,其中P(z)和Q(z)为多项式,Q0(z)不恒为0.令f(z)在|z|=r上的最大值为M,存在一个适当的ρ(0<ρ<∞)使得,若

则实轴的每个点属于f(z)的最后集[41].

波利亚在函数最后集工作的最后一篇论文是“连续阶导数的零点:一个例子”.该文讨论了特殊的亚纯函数的最后集,由无穷条平行直线y=(2n−1)π构成,最后集之外无任意阶导数的零点.波利亚在文末给出了一个优美的定理:令f(w)=tanw,若f(w)的第n阶导数在w处为0,则w为n阶导数的单重零点,w的实部是π的整倍数,但未证.古斯蒂 (M.Gusti)在 “亚纯和整函数的最后集”(1987)中给出证明[42],马丹(S.Madan)在2014年也对该例进行了探讨[43].申在“关于tan(k)z的零点”(1991)中进一步对此研究[44].

4 后续数学家关于函数最后集理论的研究

波利亚引入的最后集理论引起了众多学者的关注,产生了许多有意义的结果.

4.1 微分施于函数的最后集

罗德斯特伦(H.Rådström)受波利亚、奥兰德等人的影响,在1948年研究解析函数的最后集.他以幂级数的形式表示解析函数,阐述了系数和导数零点之关系,并以此证明了波利亚关于亚纯函数的最后集定理[45].海曼和欣卡宁(A.Hinkkanen)在2001年受罗德斯特伦工作影响考虑了是否一个亚纯函数的最后集可以以函数导数的对数导数的序列描述的问题,研究了函数的最后集和正交族的关系[46].

由波利亚的猜想A,B,自然引出一个问题,是否任何一个集合可为某些整函数的最后集.库瓦里(T.K˝ovári)在1956年证明存在一个整函数,它的最后集是整个平面[47].该逆问题的进一步解答由埃德雷、麦克兰尼在“一个整函数导数的零点”(1957)中给出肯定回答.这两位学者同时独立完成证明,幸好被及时发现,免于重复发表.

设H(C)为在紧致开拓扑下取的整函数空间,麦克兰妮在1952年给出了一个微分定理:存在整函数f(z),对于其连续阶导数序列在H(C)中稠密[48].利用这一结果,格斯纳,夏皮罗(J.H.Shapiro)在1987年通过证明一个整函数导数序列零点的最后集一般为整个黎曼面,完善了波利亚和麦克兰妮的最后集理论[49].

萧氏、普拉瑟在1982年对于具有代数奇点的函数给出了函数的最后集定理,阐述了关于连续阶导数的零点如何迁移到最后集的定量结果[50].海勒斯坦、申、威廉森(J.Williamson)在1983年证明,阶大于1的波利亚-舒尔函数以整个实轴为最后集[51].申在1986年利用最速降线法,证明了在一定条件下,偶拉盖尔-波利亚函数的最后集为整个实轴[52].

古斯蒂在“亚纯和整函数的最后集”(1987)中,确定了某些整函数连续阶导数的零点集,并表明在这些函数的导数和某些多项式之间存在紧密关系,利用这些可以确定零点分布.若一个整函数只有实根,则这个函数的导数可能有非实根.这表明整函数的型和阶影响着这些函数连续阶导数的零点趋势.

格斯纳以其博士论文为基础,在1984年对于有限阶的(包括分数阶在内)某类整函数,一些最大最小型的及指数型幂级数的和的函数建立了一个与波利亚郡定理类似的定理.格斯纳、桑斯(L.R.Sons)在“具有阿达玛缺项整函数导数的零点”(1986),格斯纳在“在单位圆内具有阿达玛缺项级数的连续阶导数的零点”(1989)及“具有阿达玛缺项级数的连续阶导数的零点”(1993)等文章中研究了具有阿达玛缺项级数的最后集问题[56].

包斯、雷迪在 “整函数连续阶导数的零点”(1973),雷迪在 “整函数零点的导数”(1974),施思冒(T.Sheil-Small)在 “实整函数导数的零点和威曼猜想”(1989)等研究了当n趋于无穷大时,导数零点的迁移性问题.但是当n很小时,情况如何呢?苏贤南(Su Hyeon Namn)在1997年填补了这一空白.他把排队网状系统问题形式化为一个一般的数学问题,称为“迁移临界点”猜想.该猜想断言:无论n为何值,存在有理函数的连续阶导数的零点以加速的速率迁移[57].哈雷尔(A.Harel)、苏贤南、斯特姆(J.Sturm)在1999年继续研究,证明若f(z)为阶小于1的整函数,其根全部为实的,则f(k)(z)的最小根随k增加而增加.哈雷尔等人根据柯夫、科尔达斯、史密斯在“整函数导数的零点和波利亚-威曼猜想”(1987)中的“对充分大的n,f(n)(z)的零点全为实的”事实,证明,在这种条件下,导数的零点分散趋于无穷[58].应当指出的是,贡察夫在1930年的上述文章中已有这种思想的端倪,威尔夫(M.S.Wilf)在“对于一类整函数的比当定理”(1962)中对此也有阐述[59].

魏斯(M.Weiss)在2003年从几何背景探讨了在双曲面内自守函数连续阶导数零点的聚集问题,把波利亚关于亚纯函数的最后集结果一般化[60].博格瓦德(R.Bögvad),黑格 (C.Hägg)在2017年对有理函数,P,Q为互质多项式(Q̸=0),从测度理论角度对其最后集进行了研究[61].同年,黑格对f(z)=R(z)eT(z),R(z)为至少有两个极点(所有极点都不同)的有理函数,T(z)为多项式,也从测度理论角度对其最后集进行研究[62].

值得一提的是,与函数最后集有关的一个有意义的问题由埃尔多斯提出,记载在海曼的“函数理论研究问题”(1967)的第17页问题2.30中.该问题是,若在复平面内的集合列{Sk},每个集合无有限极限点,是否存在一个正整数列{nk}和一个超越整函数f(z)使得f(nk)(z)=0,z∈Sk.该问题由巴特(K.Barth)、施耐德(W.Schneider)在 1972年证明[63].勋伯格在 “整函数连续阶导数的零点 II”(1976)中更深入研究,并提出如下猜想:若f(z)为不恒等于 0的指数类型δ的整函数,使得每个f(v)(z),v=0,1,2,···在内至少有k个零点,则δ≥π.f(z)=cos(πz)表明π对于这个不等式为最佳常数[64].这个问题与确定惠特克常数有关.关于惠特克常数的确定及其历史发展可见于“惠特克常数”(1974)中[65].

4.2 算子运算施于函数的最后集

当微分运算由其它算子代替时,函数零点的描述结果是否仍然成立?这个问题在波利亚的工作中已有研究.当连续阶导数由其它算子的连续迭代代替时,施于解析或整函数算子的迭代的零点分布受提到的算子,整函数的阶或解析函数的增长的影响.

对于寻找施于解析函数的微分算子的连续迭代的零点的动机可在波利亚的一系列论文中找到源头.在对拉盖尔工作研究的基础上,波利亚、舒尔在“在代数方程理论中的两种因子序列”(1913)中把一个多项式或有实根或有相同符号的实根转化为一个通过某一序列和原始函数的第k项相乘得到只有实根的函数,这一工作在列文“整函数零点分布”(1960)中有详细介绍.在这篇文章之后,波利亚在“阶为0和1的整函数的代数研究”(1915)中探讨了微分算子应用于一个只有实根的整函数上对实根的影响.柯夫、科尔达斯在1977年给出了代数域而不是实数域的乘积序列结果[66],在“多项式和整函数零点分布的一个不等式”(1981)中研究了不能增加实多项式的非实根数的乘积序列.在其著作中又给出了更为全面深入的研究[67].

包斯在1978年对在无穷处解析的函数的连续阶导数的零点进行了考察,证明了下列定理:令非常值函数F(w)=∑bnw−n在无穷处解析,则存在c>0,对充分大的n,F(n)(w)在|w|=nc外没有有限零点[68].包斯的有关思想可在威德(D.V.Widder)“拉普拉斯逆变换和相关矩问题”(1934)中找到端倪.包斯的结果在萧氏,普拉瑟“连续阶导数的零点和施于解析函数的迭代算子”(1980)中一般化[69].

普拉瑟受波利亚关于施于解析函数迭代算子的零点行为的论文影响,对于三角多项式和一阶正常型的整函数的有限傅里叶变换的最后集问题进行了深入研究,涉及的论文有,包斯和普拉瑟“施于有限傅里叶变换算子的最后集”(1979),普拉瑟“平衡三角多项式的导数的零点”(1979),普拉瑟“关于最后集的新老定理”(1981).对于阶为1到2之间的一些整函数可以表示为傅里叶积分,在“可表示为傅里叶积分的整函数类的最后集”(1981),确定了该类函数对一些微分算子的最后集.在1984年对施于函数算子的零点和解析性问题的已有定理和问题进一步研究[70].他在同年证明了下列定理:令f(z)为一个阶为1,正常型的实整函数,在实轴上有界,L=ϕ(D),,ϕ(w)为 LP 类函数,ϕ(0)=0,则f(z)关于L的最后集包含在实轴或为离散子集或为整个实轴[71].

5 结语

当n增加时,函数的第n阶导数的零点如何表现是波利亚研究的一个重要领域,并激起了众多学者的研究.波利亚对微分运算下函数零点问题进行了深入研究,获得了一些重要成果,其中之一便有函数的最后集理论.他给出了函数最后集的几何描述和概念、给出了亚纯函数和一些整函数的最后集定理,提出了一些重要的研究方法和思想,特别是提出了3个有重要影响的猜想,奠定了其后数学家在这个领域研究的基础.

波利亚的最后集理论在一定程度上支持了哥德堡(Gol′dberg)猜想.哥德堡猜想断言:f(z)的不同极点的频率由f(k)(z)的零点控制.波利亚的最后集定理表明,若f(z)至少有两个极点,则对充分大的k,f(k)(z)至少有一个零点.但该定理未能揭示出导数零点频率的具体信息.该问题由兰利(J.Langley)在“亚纯函数导数的零点”中研究[72].波利亚的最后集理论对黎曼猜想的解决也有重要作用[73].

一个整函数连续阶导数的零点分布是一个活跃的主题,其他学者从其它视角对函数的最后集问题进行研究,进一步丰富了函数的最后集理论.格斯纳在1985年研究了函数在最后集中点的连续阶导数零点的增长率问题[74].弗让柯、兰利在1999年研究了线性微分多项式的零点问题[75].奥斯特罗夫斯基 (I.Ostrovskii)和乌雷宁(A.Üreyen)在2003年研究了一个整函数的零点集和最大模点的距离问题[76].迈拉斯(T.Meyrath)、缪勒(J.Müller)在2013年研究了亚纯函数的连续阶导数序列在最后集点中的行为[77].

波利亚的函数的最后集理论影响深远,一方面和该理论在函数零点理论中的重要性有关,值得学者们研究与思考;另一方面,在研究函数的最后集理论的学者中,他们中有的是师生关系,有的是学术上多年合作的伙伴.如奥兰德是威曼的学生,海勒斯坦是埃德雷的学生,格斯纳为海勒斯坦的学生等.波利亚、威曼、埃德雷、普拉瑟、桑斯等人之间都有信件往来和学术交流,足见数学家之间的广泛交流和合作也是该理论得以传播的重要途径.