基于少数参数表征的西红柿形态三维几何建模

刘 莹 王满生 曲文娟 马海乐 潘忠礼 蒋群辉

(1. 江苏大学食品物理加工研究院，江苏 镇江 212013；2. 中国农业科学院麻类研究所，湖南 长沙 410205；3. 美国加州大学戴维斯分校生物与农业工程系，美国 加州 95616；4. 镇江美博红外科技有限公司，江苏 镇江 212013)

西红柿是中国主要农作物之一，产量和消费量逐年上升，其加工产品种类也越来越多。但目前对于西红柿果实几何建模的研究相对薄弱，其精深加工程度远远落后于世界先进水平，产品附加值低。

近年来，随着农业基础知识的拓宽和计算机图像处理技术的不断发展，农作物几何建模技术应运而生，目前国内外学者已经开发了一些几何模型用以模拟农业材料，例如简化几何模型[1]、三维重建模型[2-3]以及参数化建模方法[4]等。其中，参数化建模技术[5]是目前最常用的建模方法，它是用参数来构造产品的几何形态，能够对产品进行快速建模，为产品的快速可视化提供了基础。但是目前参数化几何建模方法在西红柿形状表征方面的应用依然具有较大的挑战：首先，西红柿精准的几何模型还没有完全发展起来。西红柿呈较扁的椭圆形[6-8]，茎花轴向尺寸均匀，特别的是，西红柿茎端(茎部瘢痕)的缩进特征是其一个重要的局部形状特征[6-7,9]，直接影响着其剥皮、分选、质检等一系列加工操作[10-12]，但目前未见有对西红柿茎端局部缩进特征进行精确描述的相关研究报道，现有研究[13-14]报道的曲面和自由曲线的参数化建模方法通常是建立在物体近似曲面的几何形态基础上的，不能准确表征西红柿茎端局部缩进的特征，因此无法应用于西红柿相关的计算机辅助设计和仿真中。而且曲面和自由曲线几何模型的表征参数较多，不仅有位置参数，还有积分参数和微分参数[5]，包含了大量的数字化数据，数据处理复杂。

研究拟通过建立少数参数表征的三维几何模型快速且直观地构造出西红柿的真实几何形状，准确捕捉其重要的茎端局部缩进特征，为西红柿相关的计算机辅助设计、仿真以及剥皮、分选、质检等一系列加工提供基础数据，为其产业精深加工提供技术支撑。

1 材料与方法

1.1 试验原料

西红柿：无机械和虫咬等伤害，市售。

1.2 主要仪器与设备

电子天平：SQP型，北京赛多利斯科技有限公司；

游标卡尺：MNT-150型，上海美耐特实业有限公司。

1.3 试验方法

1.3.1 西红柿尺寸的测量和几何关系建立 表征西红柿形态属性的主要参数包括总高度(H)、最大直径到底部的垂直位置(P)、最大直径(W)、肩高(S)、花端曲率半径(R90)和茎端曲率半径(R270)(见图1)。使用精度0.1 mm的游标卡尺来测量上述参数。

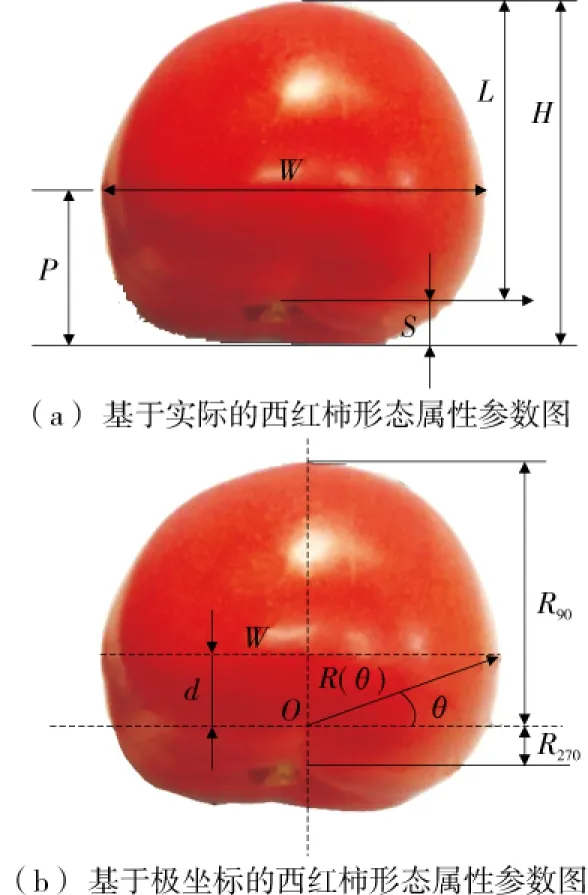
图1 西红柿的形态属性参数Figure 1 Morphological attribute parameters of tomato

由图1可知，各参数之间存在如下关系：

L=H-S，

(1)

L=R90+R270，

(2)

式中：

L——西红柿长度，mm；

R90——花端曲率半径，mm；

R270——茎端曲率半径，mm；

H——西红柿总高度，mm；

S——西红柿肩高，mm。

根据所选取西红柿的形态特征，由于其最大直径(W)并不等于果实高度中点所对应的直径，而是位于其水平轴的下方，因此d表示为：

d=H-(P+R90)。

(3)

1.3.2 西红柿几何模型的构建 先采用正弦幂级数的三次项[15]来描述西红柿的曲面形状，再通过引入4个形状描述系数(a、b、c1、c2)来精确表征西红柿的茎端局部缩进特征，具体几何模型的表达式为：

(4)

式中：

R(θ)——坐标原点(O)到西红柿表面不同位置的径向距离，mm；

θ——极坐标的角度；

a、b、c1和c2——形状描述系数。

1.3.3 西红柿几何模型描述系数的计算 为定量描述西红柿形状，需要确定4个形状描述系数(a、b、c1、c2)，按照如下步骤计算：

(1) 确定系数“a”：当θ= -π/2和π/2时，式(4)可以简化为式(5)和式(6)：

R90=a(1+c1+c2)，

(5)

R270=a(1-c1-c2)。

(6)

通过将式(5)和式(6)相加合并得：

(7)

由于R90和R270还满足式(1)和式(2)的关系，因此代入式(7)，a可以表示为：

(8)

(2) 确定系数“b”：西红柿果实在不同位置上的直径W(θ)可通过θ来表示，其函数：

W(θ)=2R(θ)cos(θ)。

(9)

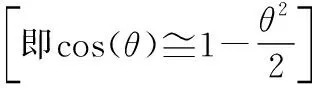
(10)

根据最大直径W(θ)在闭区间[0,2π]范围内的求导结果等于零，得出式(10)中θ应满足以下条件：

(11)

此外，由于函数W(θ)的最大值是在端点处或临界点处得出的，从几何角度看，如果仅观察最大直径的一半(W/2)，θw也应满足直角三角[如图1(b)所示]的关系：

(12)

将式(12)代入式(11)，求解系数“b”为：

(13)

(3) 确定系数“c2”：通过R90除以R270，根据式(5)和式(6)，系数“c1”和“c2”之间的关系可以表示为：

(14)

或

(15)

将式(14)、式(15)和式(2)重新整合，c2可以用c1表示为：

(16)

(4) 确定系数“c1”：另一个直角三角[如图1(b)所示]关系：

(17)

将式(17)的左侧以式(4)的形式展开，将式(8)、式(13)、式(16)中的系数a、b、c2代入式(17)中得到：

(18)

此外，c1可以通过假设二阶或更高阶的sin(θw)来表示，函数的阶次越高，收敛性和计算精度越高[18]，式(18)可变为：

(19)

将式(3)、式(8)、式(12)代入式(19)，由此得出c1为：

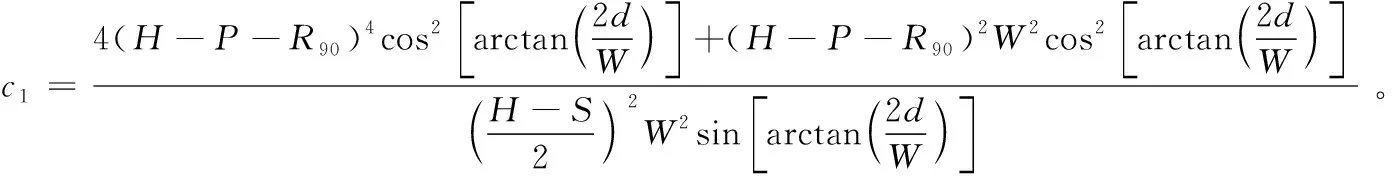
(20)

上述西红柿形状描述系数的具体计算数学方程详见表1，此外还给出了4个系数计算时需要用到的实际测量尺寸参数。

表1 西红柿形状系数的数学方程及与西红柿实际尺寸参数的关联

1.3.4 西红柿质量和表面积的预测值计算和实测值测定

假设西红柿是围绕其茎花对称轴旋转的固体，可以根据帕普斯第一定理[19]，推导出西红柿体积的计算公式：

(21)

式中：

V——西红柿体积，mm3；

θ1——角积分下限；

θ2——角积分上限。

假设西红柿果实密度为常数，可以用式(22)计算西红柿质量(m)。

m=

(22)

根据帕普斯第二定理[19]和辛普森公式[20]计算西红柿表面积(SA)，其计算公式如下：

(23)

通过式(22)和式(23)计算获得西红柿质量和表面积的预测值。此外，根据阿基米德原理，采用0.2 g/mL蔗糖溶液体积置换法测定西红柿的密度[21]。使用电子天平测定西红柿质量的实测值。采用圆台法[22]测定西红柿表面积的实测值。

分别以相对百分误差(ERPE)、均方根误差(ERMSE)和确定系数(R2)来反映预测值与实测值之间拟合度的优劣，其中ERPE和ERMSE计算公式：

(24)

(25)

式中：

MV——实测值；

PV——预测值；

n——样本量。

2 结果与讨论

2.1 西红柿几何模型中描述系数的计算

取超市购买的75个西红柿为样本，测定其实际尺寸参数，实测结果如表2所示。由表2可知，将实测值代入表1中的数学方程计算获得几何模型中的4个描述系数，描述系数a和b的平均值(24.50，32.82 mm)非常接近实测果实高度(H=54.97 mm)和最大直径(W=65.09 mm)的一半，表明二者描述系数的数值大小与西红柿实测尺寸参数直接相关，可以由H和W直接计算获得。此外由表1的计算方程还发现，描述系数c1和c2(0.33，0.11 mm)也与西红柿实测尺寸参数H、W、P、S、R90直接相关。同样地，Narushin等[23]采用参数方程描述禽蛋的形状时也发现几何模型的描述参数与实测样品的尺寸密切相关。综上所述，研究建立的西红柿形状几何模型中的4个系数均与西红柿实际尺寸参数密切相关，具有实际物理意义，可以全面表征西红柿曲面形状以及重要的茎端局部缩进特征，可在西红柿相关的计算机辅助设计、仿真等相关工程应用中发挥重要作用。

表2 西红柿实测尺寸参数与几何模型计算系数的统计描述

2.2 西红柿几何模型系数与质量和高度关系的分析

西红柿形状变化的预测受果实质量和大小的约束，如果能将西红柿质量和高度一起整合到西红柿几何模型中，对用少量的参数快速表征西红柿真实的几何形状具有重要意义。章文英等[24]在对苹果的形状进行研究时发现高度对于苹果形状的表征起到了关键性的作用。因此研究分析西红柿形状描述系数(a、b、c1、c2)与其实际质量(m)和高度(H)的关系，结果见图2和图3。根据图2中建立的两个回归方程发现，回归相关系数R2均在0.85以上，表明西红柿质量(m)与系数b、西红柿高度(H)与系数a之间存在显著的线性相关性，因此，西红柿描述系数a和b可以通过直接测量西红柿实际高度和质量来获得，比表1中通过测量W、H、P、S和R90来获得更为简便和快速，表明研究所建几何模型可以实现以少量参数对西红柿真实几何形态的快速表征。同样地，Rashidi等[25]的研究报道也得出可以通过参数简化几何模型进而准确描述猕猴桃的几何形状。

图2 系数b和a与西红柿质量(m)和高度(H)的关系Figure 2 Relationship between coefficients b and a and tomato weight (m) and height (H)

图3为系数c1和c2与西红柿质量(m)和高度(H)的关联结果，研究发现，系数c1和c2与西红柿质量和高度均无良好的线性相关性，其数值的计算仍需通过西红柿5个尺寸参数(H、S、R90、W和P)的测量来获得，这是因为c1和c2的数值大小反映了西红柿茎端缩进特征的局部细节变化，决定了其形状的均匀性和同质性[26]，而不是西红柿整体大小的变化，因此其与质量和高度的相关性较低。

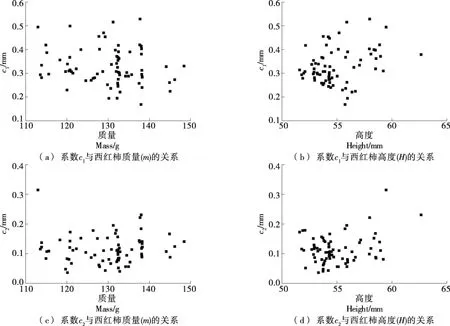
图3 系数c1和c2与西红柿质量(m)和高度(H)的关系Figure 3 Relationship between coefficients c1 and c2 and tomato weight (m) and height (H)

2.3 西红柿三维几何模型的构建

在建立的二维几何模型基础上，将西红柿剖面绕茎花对称轴旋转，得到其三维几何的转换，并将数学方程[式(4)]以及4个描述系数(a、b、c1、c2)的平均值代入MATLAB算法中创建西红柿的三维几何模型，结果见图4。由图4可知，该模型直观准确地描述了西红柿茎端局部缩进的特征，增强了模型的真实感，强化了模型的可视化功能，可以作为计算机模拟西红柿几何形状的一种直观准确的计算工具[27]。纪平等[28]也利用番茄的半径等参数采用MATLAB算法获得了果实的轮廓图像，但是其采用的MATLAB算法操作步骤较为复杂，且识别率不高，并不是一种快速表征西红柿几何形状的好方法。

图4 西红柿的三维几何模型Figure 4 Three-dimensional geometric modelof tomatoes

2.4 西红柿几何模型的验证

几何模型可以用于计算西红柿的一些几何属性，如质量[29]、体积[23,30]、表面积[28]、曲率半径[29]、圆周长[23]等。因此，研究也应用所建立的几何模型对西红柿质量和表面积等几何属性进行预测，并通过分析预测值与实测值来验证模型的准确性和可靠性。从图5发现，质量和表面积的实测值与预测值之间均存在良好的线性相关性。由表3可知，质量实测值与预测值之间的ERMSE值为10.11，ERPE为5.46%，R2为0.85，由已有报道[31]得知，该模型误差在可接受的范围内，表明质量实测值与理论预测值之间存在良好的线性相关性；表面积实测值与预测值之间的ERMSE值为44.75，ERPE为10.24%，R2为0.81，主要是由于西红柿个体差异较大造成的，但总体而言，表面积实测值与预测值之间具有较高的拟合精度。这与王浩云等[30]研究发现苹果的外形指标与真实值之间具有较高相关性的结论一致。由此得出，研究所建西红柿三维几何模型可以用于量化西红柿的质量和表面积几何属性，是一种快速、准确表征西红柿几何形状的新型方法。

图5 西红柿质量和表面积的预测值与实测值的比较Figure 5 Comparison of predicted and measured values of tomato weight and surface area

表3 西红柿几何模型的拟合度检验结果Table 3 Fitting test results of tomato geometric model

理想状况下是通过测定西红柿边界上每个点的曲率半径来捕获西红柿形状的所有特征，然而，这种方法测量效率低且计算复杂。为解决这些问题，研究构建了一个以少数参数表征西红柿形状的三维几何模型，实现了对西红柿真实几何形状的直观、精准且快速表征。此外，Datta等[32]认为几何建模的最终目的是应用于实际加工中。因此研究又将建立模型应用于西红柿质量和表面积等几何属性的预测，可为西红柿相关加工产业的科学合理设计提供便利[33]，可将其作为原料模型用于脱皮热处理过程中的传热模拟以及设备加热均匀性优化的依据，还可为西红柿其他加工工程应用推荐合适的参数，例如，在水果连续化加工作业中可以通过原料模型快速地估计水果形状和大小，实现对质量检验对象的准确定位等[34]。综上，西红柿几何形态的定量描述满足了其形态表征设计需求，可适用于各种西红柿加工技术和相关机械装备的设计，因此研究建立的几何模型具有良好的实用价值。

3 结论

研究根据尺寸参数和形状描述系数精确地描述了西红柿的茎端局部缩进特征，计算获得形态描述系数a、b、c1、c2的适用范围分别为21.78～28.58，30.50～34.54，0.19～0.53，0.04～0.31 mm，具有较宽的适用性。研究发现描述系数a和b与西红柿实际高度和质量高度线性相关(R2>0.85)，说明该几何模型可以实现以少量的参数快速表征西红柿真实几何形态的目的。实际应用中，质量和表面积实测值与预测值之间的预测效果良好，表明该模型可以用于量化西红柿质量和表面积等几何属性。研究建立的西红柿模型能够直观、迅速且精确地表征西红柿的几何形状，可以满足西红柿形态表征设计的需求，在西红柿相关的计算机辅助设计和仿真中具有良好的应用潜力。西红柿几何模型中的形态描述系数与实际样品尺寸参数之间具有线性相关性的原因主要体现于原料的自身特性，遗传育种能够保持产品尺寸与整体形状的相对稳定。但是，西红柿品种的不同依旧会导致形状特征的差异。因此，有必要对不同品种的西红柿形状描述系数展开深入研究，进一步完善几何模型，拓宽其适用性。