“情境创设”的构建及思考

王四宝

最近，笔者听了8位初中数学教师的授课比赛，他们的授课内容是义务教育课程标准实验教科书八年级上3.6“三角形、梯形的中位线”第一课时（苏科版）。

听课过程中，8位老师在课堂情境创设、实践活动等部分都进行了深入研究和认真设计，课堂精彩纷呈。学生能够在老师的引导下进行自主学习和合作学习，提高了自身对数学知识的认识和运用能力。

一、教学片段

上课开始，教师分发教学材料，每个学生都有一张三角形纸片，但是属于不同的三角形，并确保同桌的两个学生得到不一样的三角形纸片。

师：请同学们自己想一想，如何将一个三角形剪成两部分，并且使这两个部分可以组合成一个新的平行四边形？（教师提出问题之后，走下讲台，与部分学生交流。3分钟以后，教师询问学生是否完成时，只有四位学生表示自己按照要求拼出了一个平行四边形。）

师：请大家分组交流。

（前后排的学生组成小组，通过小组合作学习进行探索。其间学生相互提出意见，开展交流，相互帮助，2分钟过去了，当老师询问进度时，有近一半的学生举手表示自己已经完成剪和拼的过程。）

师：下面请一位学生来和大家分享一下自己的思路。

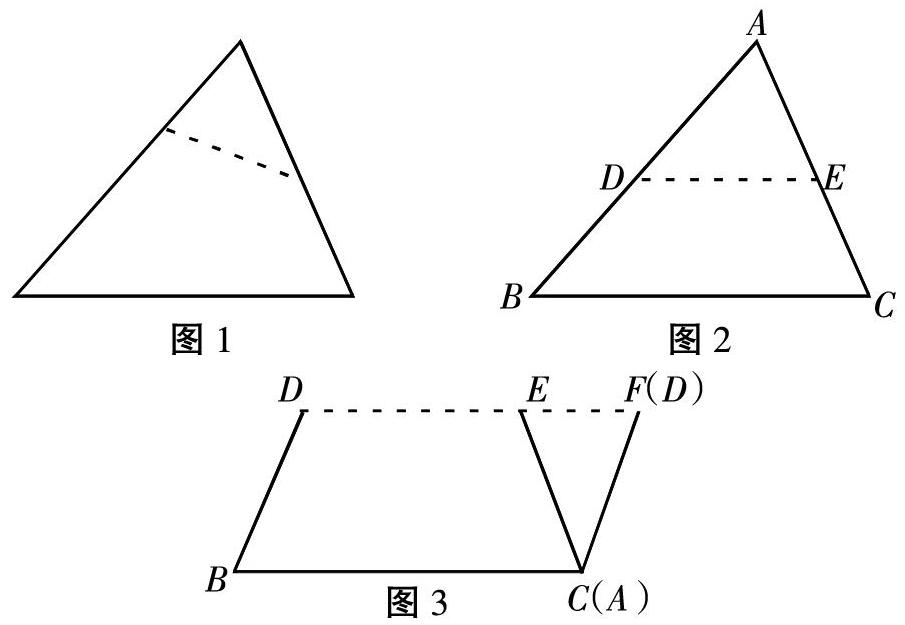
生1：（学生通过实物投影仪，演示自己剪出三个部分，并拼成一个平行四边形的过程。）一开始，我也走了弯路，把自己的三角形纸片剪成了图一，我没有成功地拼出一个四边形，更加不用说平行四边形了。但是，这次失败的经历让我思考：要拼出一个平行四边形需要什么条件。我就把这个问题提了出来，同学们跟我讨论。我们认为要想剪、拼成一个平行四边形，剪出的小三角形必须有两边与剩余四边形两边相等（即图2中AD=DB，AE=EC）。于是，我马上有了思路，我先将△ABC折叠得到AB的中点D，然后用同样的办法找到AC的中点E;DE就是我要剪下去的那一刀。剪完以后，我将△ADE绕着点E按顺时针方向旋转180°到△CEF的位置，就拼好了平行四边形BCFD（如图3）。

师：这位同学的做法对吗？你们如何判定这是一个平行四边形？

生2：他的做法是对的，我也是这么做的。

生3：这位同学最后得到的四边形BCFD中CF與BD平行且相等，所以是平行四边形。

师：（再次以动画演示学生的操作之后）其他同学有不同的意见吗？

（学生摇头表示没有。）

师：都没有意见吗？

生4：（有些犹豫，但想了一下还是大胆说出）我有一个疑问。生1操作以后的图形BCFD一定是四边形吗？我觉得需要对EF在DE的延长线上加以说明，这样才能证明点D、E、F在同一条直线上。

师：大家听懂了吗？

生：（集体回答）懂了。

师：考虑问题需要全面细致，相信听完生4的回答大家都会有启发。

下面就让我们来学习三角形中位线与第三边的关系……

二、点评赏析

与这位教师处理方式相似的还有三位，他们的处理方式有以下几个特点：

1.源于课本，高于课本

与其他两位授课不够成功的教师相比，这四位教师都是在课本的基础上自行创设了情境开展教学，结合学生学情，有创造性地对教学活动做了调整，可谓“源于课本，高于课本”。首先教师抛出研究问题;其次提供给学生进行探究的三角形纸片，并且形状都有所区别，要求学生进行操作、思考;最后组织学生有序陈述自己的探究过程，使全体学生都有不同程度的提高。这种处理方式有助于学生亲身经历知识的形成过程，从而更好地理解数学知识的意义，使学生的思维品质也得到良好的发展。

2.给学生创设探索、思考的时间与空间

问题提出3分钟后，只有4位学生举手示意完成剪、拼的操作过程时，教师并没有着急，又要求学生分组进行探讨，体现了这位教师高超的课堂驾驭能力，真正地在教学活动中发扬教学民主，给学生探索问题留有足够的时间。在学生展示自己剪和拼的过程后，老师再次提出疑问，问大家是否还有不同意见。这个问题又掀起波澜，引发学生进一步思考，为锻炼学生数学思维能力和数学探索能力提供了帮助。

三、结语

科学有效地组织教学活动是永恒的课题。实践证明，创设情境，让学生在“真实”的情境下开展学习具有显著优势，因此，教师需要持续研究教材，观察学生，对自己的课堂进行不断改进和优化，才能让课堂绽放活力，让学生获得成长。