基于动态啮合力的人字齿轮摩擦因数分析
2021-10-11唐小林
王 云, 杨 为, 唐小林
(1.重庆大学 机械传动国家重点实验室,重庆 400044;2.重庆大学 机械与运载工程学院,重庆 400044)
多种因素会造成齿轮传动系统的功率损失,其中齿面摩擦功率损失占比大,机械传动效率是衡量传动系统品质的关键指标之一。一直以来齿轮传动系统的动力学特性、润滑特性是研究热点[1-2]。王明凯等[3]建立了双渐开线齿轮传动摩擦动力学模型,研究了混合弹流润滑特性与动力学之间的耦合作用。陆凤霞等[4]建立了人字齿轮副动力学模型,采用弹流润滑摩擦因数经验公式分析了齿面摩擦对人字齿轮动力学特性的影响规律,但是实际工况下人字齿轮副处于混合润滑状态,研究中未考虑齿面摩擦导致的齿面温升的影响。袁冰等[5]基于Timoshenko梁理论和有限单元法,引入时变啮合刚度和综合啮合误差,建立了人字齿轮副系统动力学模型,研究了齿距累积误差对人字齿轮系统动态特性的影响规律。苟向锋等[6-7]考虑齿面闪温对时变啮合刚度的影响,建立了单级直齿圆柱齿轮系统动力学模型,分析了其对非线性分岔特性的影响。林腾蛟等[8]基于热弹流润滑理论获得了人字星型齿轮不同表面粗糙度下的油膜承载比及摩擦因数,结合齿面接触载荷和滑移速度,计算得到了齿面热流密度分布。菅光霄等[9]计及齿轮副的时变啮合刚度和表面粗糙度,建立了6自由度齿轮系统动力学模型,开展了动、静两种载荷模型下齿轮副弹流润滑特性的研究。董辉立等[10]建立了渐开线齿轮有限长线接触弹流润滑模型,分析了干摩擦与润滑条件下不同压力分布的特征以及动载荷对油膜分布的影响规律,其动力学模型中只考虑了扭转自由度。薛建华等[11]建立了动载荷下的瞬态热弹流分析模型,分析了啮合过程中的油膜最大压力、油膜厚度以及齿面闪温随时间变化的规律。Li等[12]提出了一种直齿圆柱齿轮副润滑-横向扭转动力学耦合模型,研究了表面粗糙度和润滑特性对动力学响应的影响规律。邹玉静等[13]建立了考虑摩擦的6自由度渐开线直齿轮动力学模型,研究了摩擦学特性和动力学行为以及两者之间的耦合关系。Jian等[14]建立了渐开线齿轮系统的动力学模型,详细分析了齿轮系统的振动和润滑特性,研究了不同转速和载荷下油膜刚度的变化规律。Liu等[15]提出了一种计及滑动摩擦的直齿圆柱齿轮传动系统的动力学模型,研究了小齿轮的转速对齿轮系统动力学特性的影响规律。
已公开报道的参考文献表明,研究人员对直齿、斜齿轮副进行了大量的动态特性和润滑特性研究。在对渐开线斜齿轮的动态特性和润滑研究中,大多数动力学数值计算模型中均只考虑了扭转自由,且模型中未考虑温度的影响。人字齿轮传动系统由于具有承载能力高、振动噪声小、工作平稳以及轴向力可以抵消等优点,被广泛应用于船舶、航空等高速重载齿轮传动装置中[16]。在高速重载工况下,由于啮合齿面相对滑动速度大,瞬时温升高,影响了齿轮系统的温度分布,易产生热机耦合效应,进而导致增大齿轮系统的振动与噪声,现有的参考文献鲜有涉及此方面的研究。
因此,计及齿面闪温的影响,在人字齿轮传动系统平移-扭转动力学模型的基础上,将动态啮合力用于求解混合弹流润滑摩擦因数,开展人字齿轮的动态特性和润滑特性研究,研究动态啮合力下人字齿轮啮合副摩擦因数的变化规律,对提高人字齿轮的啮合平稳性、承载能力和降低摩擦损耗等具有重要理论意义和工程实用价值。
1 人字斜齿轮动力学模型
1.1 单侧动力学模型
设左右斜齿的轴向力相互抵消,每个斜齿轮都考虑了x,y平移自由度以及绕z轴的扭转自由度θ。人字齿轮副多自由度动力学模型,如图1所示。图1中:β为螺旋角;et为综合啮合误差;αt为端面压力角;ψ为安装相位角;φ为端面啮合线与y轴夹角。左右啮合齿面节点广义坐标为

图1 人字齿轮啮合副动力学模型Fig.1 Dynamic model for herringbone gear

式中:下标p,g为主动轮和从动轮;下标i为l或r,左啮合副或右啮合副。L(t)为啮合副在啮合方向上的相对位移,可表示为

综合啮合误差et=e0sin(ωmt),其中:e0为齿轮误差平均幅值,根据齿轮制造精度选取;ωm为啮合频率。
轮齿的动态啮合力为
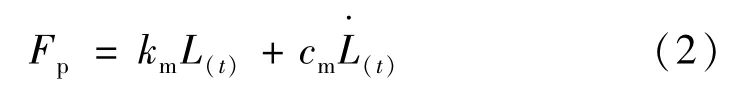
齿面摩擦力为

式中:cm为啮合副的平均阻尼,Ns/m;km为平均啮合刚度,N/m;u为摩擦因数;sgn(vs)为摩擦力方向系数;vs为啮合点相对滑动速度,m/s;sgn(x)为符号函数,其表达式为

采用Kisssoft软件计算了平均啮合刚度km,啮合阻尼cm由经验公式计算[17]。
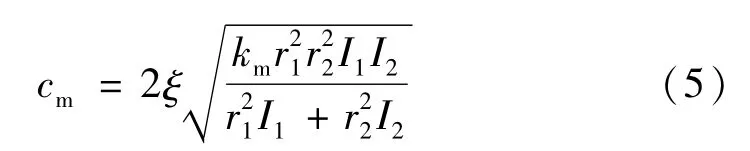
式中:r1,r2分别为两齿轮的节圆半径,m;I1,I2分别为两齿轮的转动惯量,kg·m2;ξ为齿轮副的阻尼比,通常取值范围为[0.03,0.17],研究中取为0.1。
采用拉格朗日方程建立齿轮传动系统的运动方程
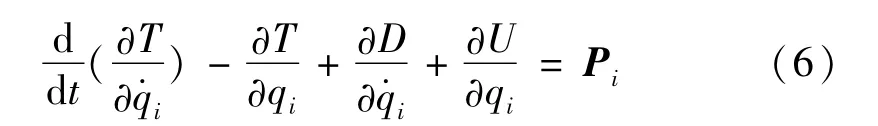
式中:T为系统动能;U为系统内力势能;D为系统对于黏性阻尼的逸散函数;qi为广义坐标;Pi为载荷列向量。
令

系统的内力势能为
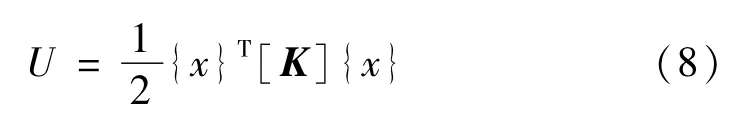
系统动能为

系统黏性阻尼的逸散函数为
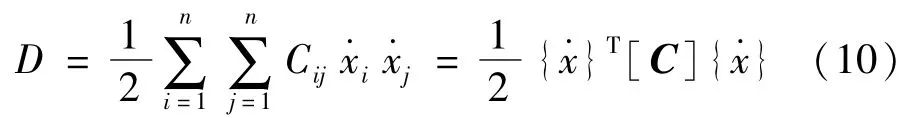
式中,[M],[C],[K]为实对称矩阵,因此可以得到
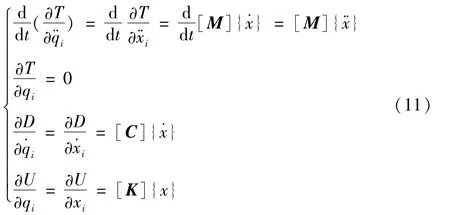
式(6)可以写成矩阵形式为
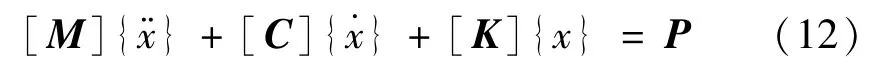
1.2 系统的动力学方程
如图2所示,人字齿轮分为三部分:左侧斜齿轮、右侧斜齿轮及中间连接结构。连接结构从右侧齿面中点到左侧齿面中点。使齿轮的总质量等于左右两侧和连接结构的单个质量之和。因此,连接结构的子矩阵为
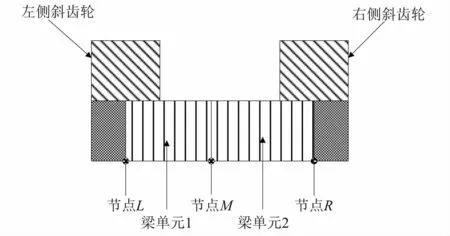
图2 人字齿轮左右斜齿梁单元连接Fig.2 Beam element for herringbone gear

式中:下标e1为梁单元1;下标e2为梁单元2。
将式(12)和式(13)定义的从右到左的耦合矩阵一起系统地装配,以获得由一对人字齿(总共12自由度)组成的人字齿轮组的整体运动方程。采用Runge-Kutta积分法,调用软件MATLAB的ode45函数进行数值求解。人字齿轮传动系统的参数如表1所示。

表1 齿轮传动参数Tab.1 Parameters of gear transmission
2 混合热弹流润滑模型
2.1 摩擦因数
混合弹流润滑摩擦因数可以通过边界润滑摩擦因数和弹流润滑摩擦因数加权和的形式表示[18]
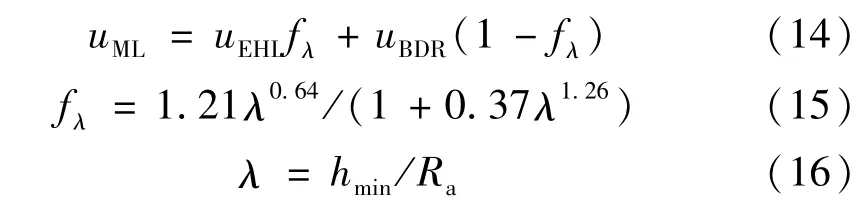
式中:uML为混合润滑条件下摩擦因数;uEHL为全膜润滑条件下摩擦因数;uBDR为边界润滑条件下摩擦因数,实验所测该系数摩擦因数在0.07~0.15;fλ为在混合润滑状态下点接触载荷分布百分比;Ra为齿面等效平均粗糙度。
由参考文献[19],人字齿轮啮合中心油膜厚度公式为

式中:η为润滑油动力黏度,Pa·s;ve为卷吸速度,m/s;ξ为黏压系数;Fn为基于动态啮合力的齿面法向载荷;R啮合点的综合曲率半径;E为等效弹性模量,单位为GPa。
弹流润滑状态是两齿面完全被油膜分开的理想状态,此时摩擦因数最小,功率损耗最小。弹流润滑摩擦因数计算公式为[20]

式中:SR为接触齿面的滑滚比;Ph为齿面最大接触应力;Ra为表面粗糙度的均方根值;b1~b9取值参考陆凤霞等的研究,具体数值如表2所示。
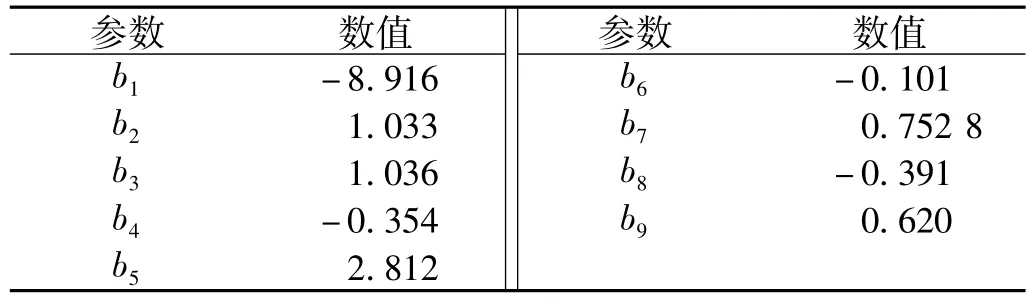
表2 参数取值Tab.2 Parameters value
由于摩擦副的载荷集中作用,接触区内的压力很高,且人字齿轮用于高速重载的场合,齿面摩擦导致齿面温升较高,因而在润滑模型中润滑油的黏压黏温效应

式中:η0为环境温度下润滑油动力黏度,Pa·s;T0为环境温度;z0,s0为无量纲常数,它们与常用的Barus黏压系数ξ及黏温系数ζ的关系为
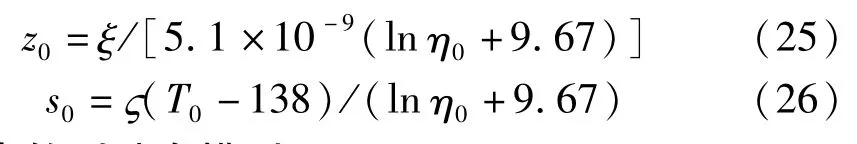
2.2 斜齿轮副啮合模型
图3所示为一对渐开线斜齿轮副的啮合过程[21]。r1,r2分别为两齿轮的节圆半径,ω1,ω2分别为两齿轮的转动角速度,αn为分度圆压力角,啮合点距节点的距离为s。啮合点以绝对速度ω1rb1沿啮合线作匀速运动,任意时刻t有:s=ω1rb1t。

图3 齿轮传动副啮合过程Fig.3 Meshing model of gear transmission
设接触线与齿面前端面的交点为K点,K点处的曲率半径分别为R1和R2。

根据渐开线齿轮的几何特点可知,在K点处,两齿面的法向曲率半径为

式中,s为啮合线上啮合点至节点的距离。
对任意时刻,两齿面相对啮合点的油膜速度及卷吸速度为
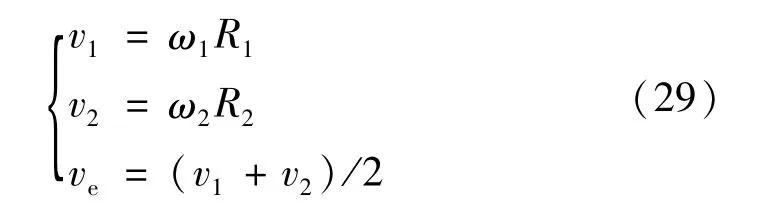
齿面间的相对滑动速度vs及滑滚比SR表示为

啮合点的Hertz接触最大应力为

如图4所示,任何摩擦表面都是由许多不同形状的微凸峰和凹谷组成。表面几何特征通常采用形貌参数来描述,其中轮廓的均方根值Ra为
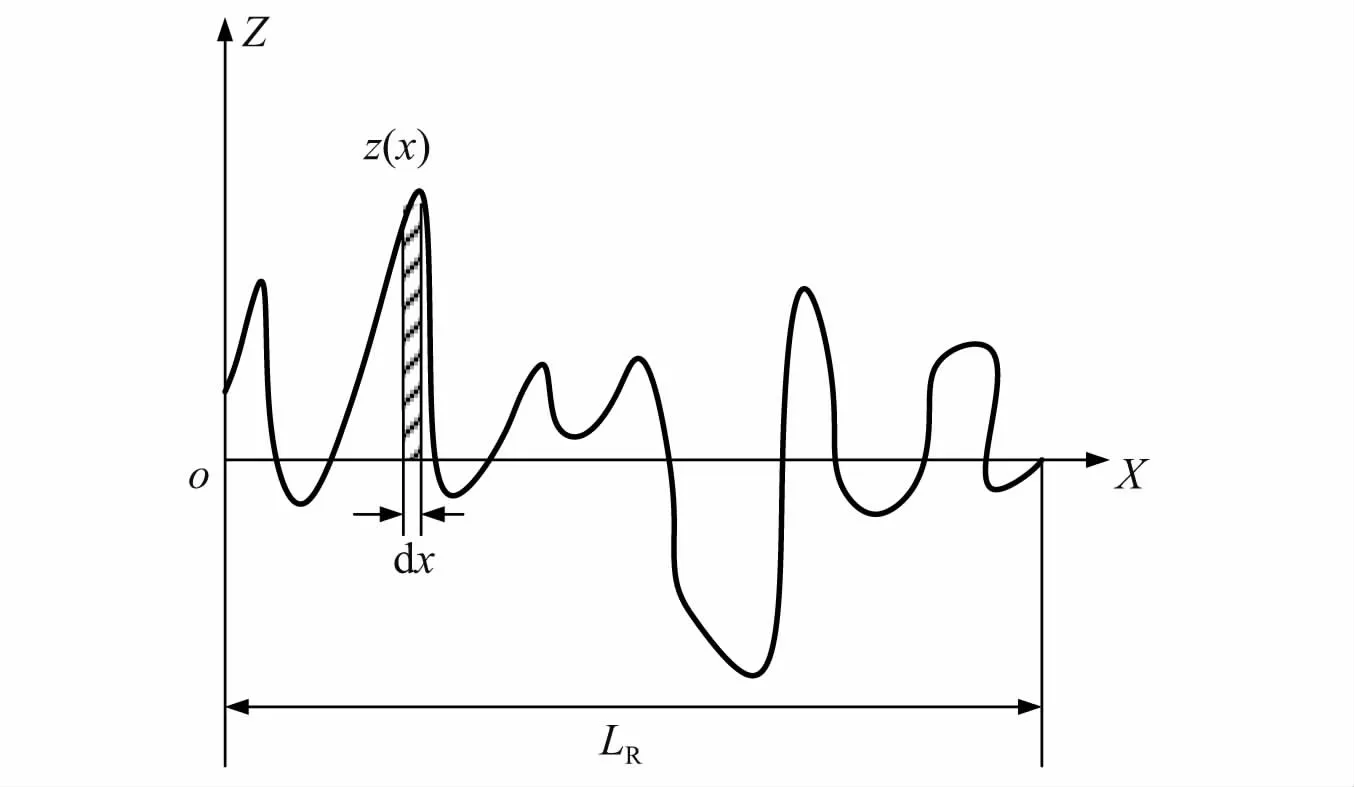
图4 表面形貌轮廓曲线Fig.4 Surface topography profile curve

式中:z(x)为各点轮廓高度;LR为测量长度;zi为各测量点的轮廓高度。
2.3 齿面接触Block闪温
齿面接触温度ΔB由本体温度ΔM和齿面瞬时闪温Δf两部分组成[22]

式中:本体温度ΔM在系统达到稳定工作状态后不再变化,此时两齿轮本体温度相同;齿面闪温Δf是由两齿面相对滑动时,摩擦消耗的能量转化的热量导致齿面局部瞬时温度升高。根据Block闪温理论,可得齿面瞬时闪温Δf的表达式。

式中:κ为斜齿轮温升系数;fe为单位齿宽上的齿面法向载荷;vi(i=1,2) 为两齿面上的切向速度;gi(i=1,2) 为两齿面的热传导系数;ρi(i=1,2)为两齿面的材料密度;ci(i=1,2)为比热容。 主、从动轮齿宽相等,由Hertz接触理论可得主、从动轮的接触带半宽B(t)表达式
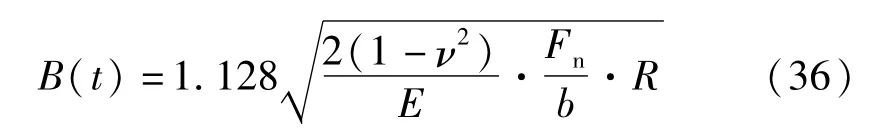
式中:v为泊松比;b为主、从动轮齿宽,mm。
3 动力学模型和润滑模型耦合计算
在获得齿轮系统的结构参数、材料参数和工况参数的基础上,对齿轮系统进行啮合分析和内部激励计算,计算齿轮啮合刚度以及卷吸速度、滑滚比等参数。在建立考虑齿面摩擦的齿轮系统多自由度动力学模型的基础上计算得到动载荷。将啮合模型计算出的结果和动载荷结合可以得到混合弹流润滑摩擦因数模型,其中还考虑了齿面温升对齿轮系统和润滑模型的影响,采取平均温升和上一次迭代的平均温升的绝对差值来判断系统是否收敛,计算流程如图5所示。
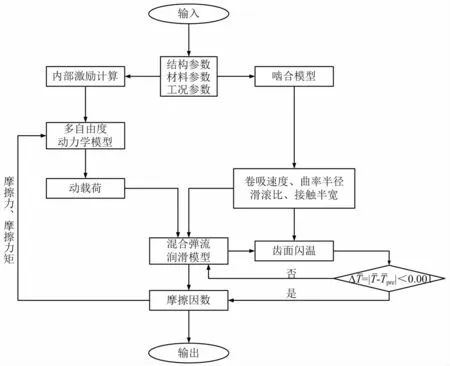
图5 技术路线Fig.5 Solution flow chart
4 结果分析和讨论
图6(a)为赫兹接触应力和综合曲率半径随啮合线的变化情况。齿轮由啮入到啮出的过程中赫兹接触应力逐渐增加,啮合点的综合曲率半径逐渐减小。如图6(b)所示,随着齿轮的啮入到啮出的过程中,滑滚比和齿面摩擦产生的闪温先减小后增大,在节点处滑滚比和齿面摩擦产生的温升为0,这是因为在节点处,两齿轮的相对滑动速度为0。图6(c)、图6(d)分别为弹流润滑摩擦因数、混合弹流润滑各啮合位置摩擦因数随负载转矩的变化情况,弹流润滑摩擦因数在啮合节点处最小,离啮合节点越远,摩擦因数越大。随着负载转矩的增大而增大,最大摩擦因数处于离节点最远处为0.065,混合弹流润滑摩擦因数也随着负载转矩的增大而增大,但是随着啮合线先缓慢增加,通过节点位置之后快速增加,其最大摩擦因数仍处于离节点最远处为0.165,大于弹流润滑摩擦因数。
图6(e)、图6(f)所示为弹流润滑摩擦因数、混合弹流润滑各啮合位置摩擦因数随齿面粗糙度的变化情况。两种摩擦因数的变化趋势一致,都是在啮合节点处最小,离啮合节点越远,摩擦因数越大,随着齿面粗糙度的增加而增加。图6(g)、图6(h)为不同啮合位置摩擦因数随齿面闪温的变化情况。齿轮在啮入到啮出的过程中,弹流润滑摩擦因数先减小后增大,随着齿面闪温的增加而减小。这是因为润滑油的黏温效应导致的;不同齿面温升对应不同的混合弹流润滑摩擦因数随啮合线的变化趋势。不考虑齿面温升和齿面温升为5℃时,混合弹流润滑摩擦因数随啮合线先缓慢增加,通过节点后快速增加,摩擦因数随着齿面闪温的增加而降低;当齿面温升为15℃和20℃时,齿轮在啮入到啮出的过程中,混合弹流摩擦因数逐渐减小。由图6(h)可知,混合弹流润滑摩擦因数随着齿面温度的升高而下降,当齿面温度升高到一定值时,摩擦因数随着齿面温度的升高而升高,这是因为齿轮啮合处于边界润滑和弹流润滑的混合润滑,温度越高导致油膜黏度下降,油膜厚度变薄。
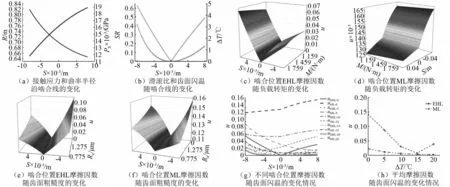
图6 稳态载荷下各参数的变化情况Fig.6 Changes of various parameters under steady-state load
如图7(a)、图7(b)所示为基于动态啮合力的膜厚分布规律,膜厚随着时间先经历一个小的波谷到波峰,然后经历一个大的波谷到波峰。图7(c)为齿面温升的分布规律,齿面温升沿啮合线先减小再增大,最小值处于啮合节点位置,这是由于离啮合节点越远,两齿轮相对滑动速度越大,齿面温升就越高。如图7(d)、图7(e)所示为弹流润滑摩擦因数和混合润滑摩擦因数分布,它们的变化趋势一致,随时间先减小然后保持平稳,这是因为齿轮系统初始的振动不平稳导致动态啮合力增大,沿啮合线先快速降低然后缓慢增加。
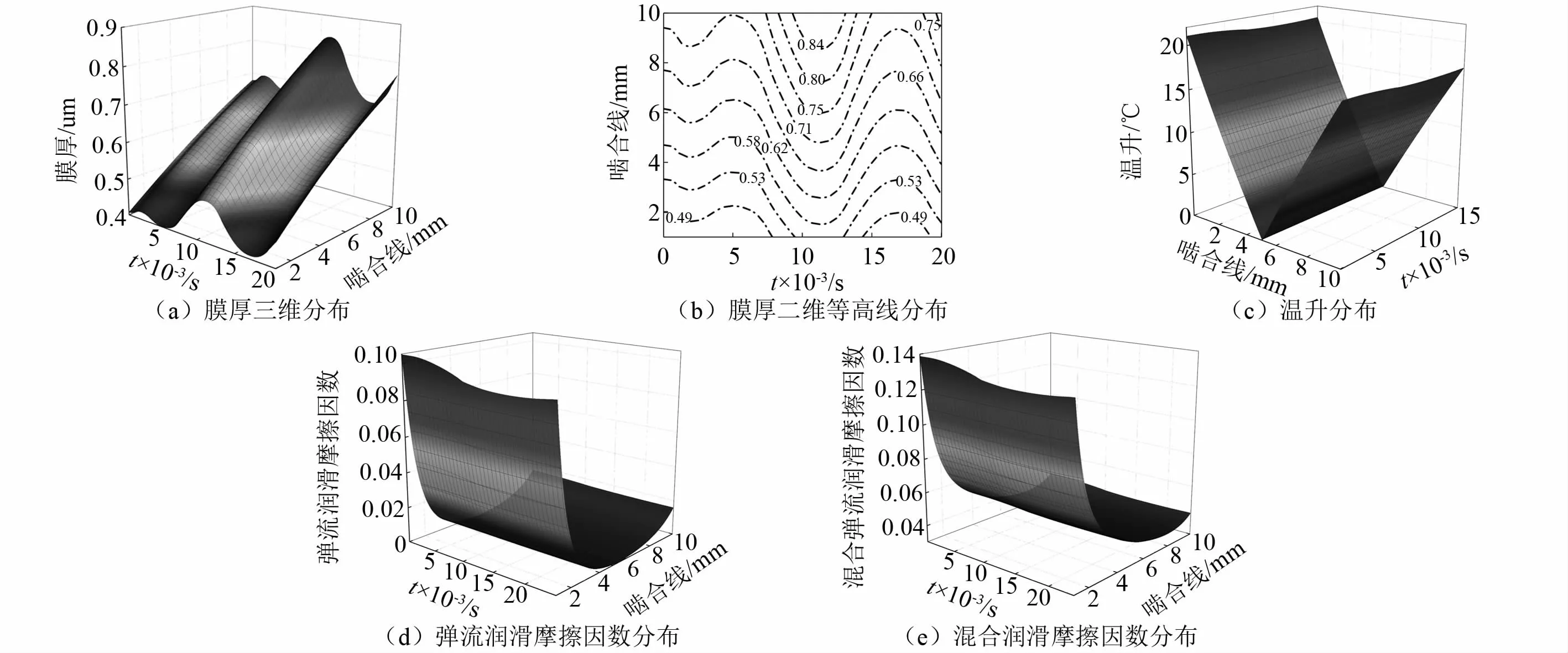
图7 基于动态啮合力的膜厚、温升和摩擦因数分布Fig.7 Distribution of film thickness,temperature rise and friction coefficient based on dynamic meshing force
从图8~图11可以看出,耦合计算和非耦合计算得出的振动位移与振动速度的变化趋势是一致的,耦合计算得到的主、从动轮x,y方向以及绕z轴扭转的振动位移和速度都高于非耦合计算结果,沿啮合线方向的振动位移、速度以及动态啮合力耦合计算结果略高于非耦合计算结果。表明齿面摩擦对齿轮系统各个方向的振动速度和振动位移都有一定程度的影响,同时也会影响齿轮系统沿啮合线方向的振动位移、振动速度以及增大动态啮合力。

图8 主动轮振动位移和振动速度Fig.8 Vibration displacement and speed of driving gear

图11 动态啮合力Fig.11 Dynamic force
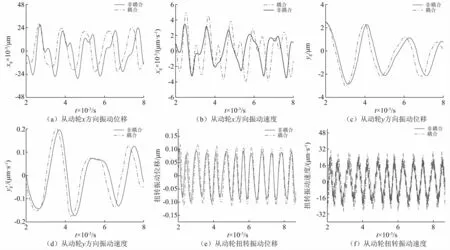
图9 从动轮振动位移和振动速度Fig.9 Vibration displacement and speed of driven gear
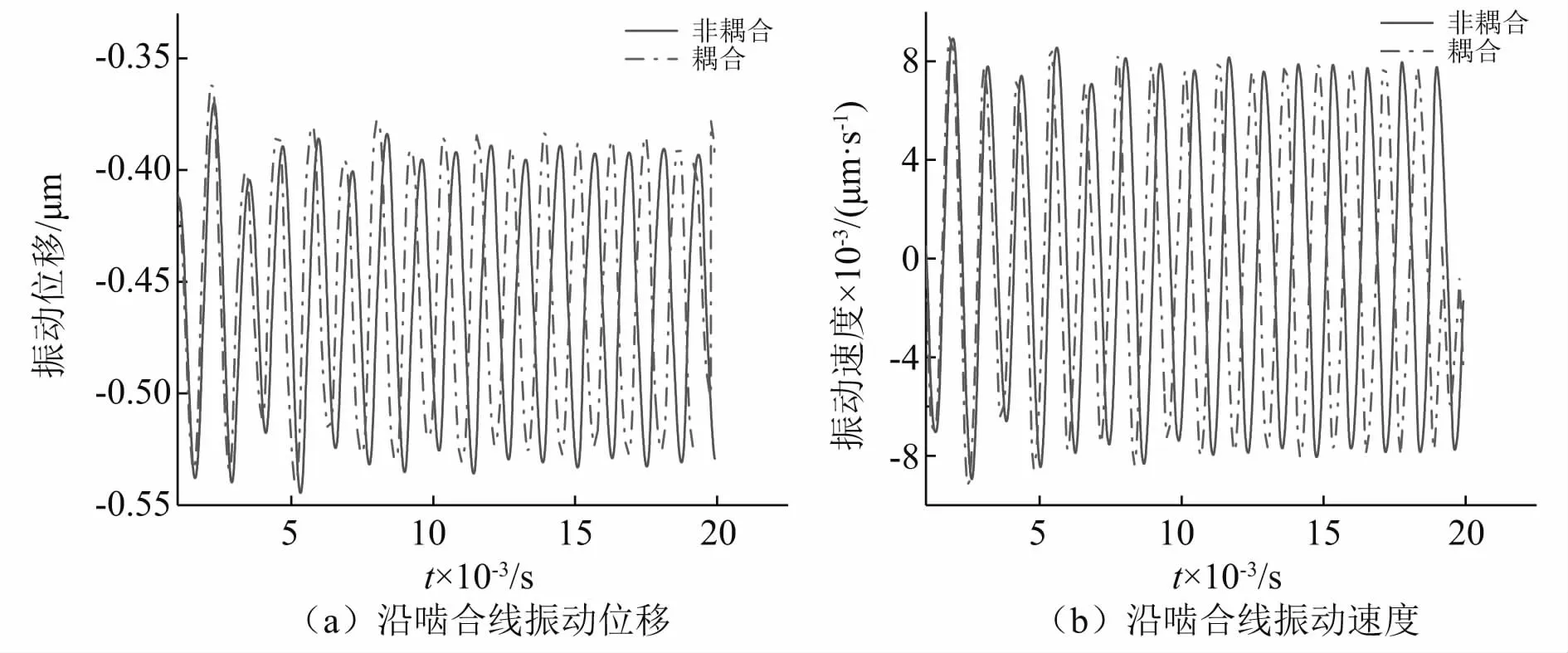
图10 沿啮合线振动位移和振动速度Fig.10 Vibration displacement and speed along meshing line
5 结 论
综合考虑时变啮合刚度、静态传递误差、齿面摩擦力和人字齿轮副啮合过程中的齿面温升效应,建立了人字齿轮多自由度动力学模型,利用混合弹流润滑摩擦因数计算模型,得到了齿面摩擦因数和齿面粗糙度、载荷的变化关系,研究了人字齿轮在耦合和非耦合状态下的振动特性,得到以下结论:
(1)通过人字齿轮副的啮合特性分析,得到了啮合过程中的等效曲率半径、赫兹接触应力、滑滚比等润滑参数变化规律。结果表明,齿轮在啮入到啮出过程中,赫兹接触应力逐渐增加,啮合点的综合曲率半径逐渐减小,滑滚比先减小后增大。
(2)啮合过程中,油膜厚度随时间呈现增大减小再增大减小的循环变化。齿轮副由啮入到啮出的过程中,膜厚逐渐增大;齿面温升先减小再增大,最小值处于啮合节点位置。摩擦因数随时间先减小然后保持平稳,齿轮由啮入到啮出过程中,摩擦因数先快速减小再缓慢增加。
(3)齿面摩擦会增大齿轮系统各个方向的振动速度和振动位移,同时也会增大齿轮的动态啮合力。
