基于多元特征感知网络的高考成绩预测

田 钰

(合肥市教育局 教育科学研究院，安徽 合肥 230071)

0 引言

随着社会对高等教育的重视程度越来越高，如何针对考生成绩进行科学的预测分析来提高教学质量,已成为教育部门关注的焦点。传统方法是利用数理统计的知识设置分数线来对考生成绩进行档次划分，难以从中挖掘影响成绩的潜在因素。因此，教育数据挖掘(Educational Data Mining, EDM)应运而生。EDM[1]运用教育学、计算机科学、统计学、心理学等多个学科的理论和技术来解决教学研究与教学实践中的问题，主要包括数据准备、数据筛选、数据处理、数据挖掘、模式评估等一系列步骤。

如何通过高效的挖掘算法帮助管理者和决策者揭示教学规律并完善教学方法，一直是EDM领域中极具挑战性的问题。国内外学者对此也进行了相关的研究。KUMARVERMA[2]使用Apriori算法对考生的历史成绩进行分析与分类，挖掘成绩间的关联规则，但该方法利用传统的Apriori算法，会产生大量频繁项集、候选项集，需要多次访问事务数据库，从而带来了巨大的I/O负载。文献[3-5]使用决策树(Decision Tree, D-T)对考生成绩进行预测，通过计算特征属性的信息熵与信息增益选择分裂属性，构建具有最大增益率的决策树来建立分类规则并分析预测模型，但是对连续的分数预测精确度较差，可能出现过度匹配的问题且容易产生过拟合的现象。ZHANG等[6]将支持向量机(Support Vector Machine, SVM)应用到高考成绩预测中，以回归分析来预测高考成绩。但是在数据的收集、对混合预测的效果等方面存在不足。DEVASIA等[7]采用朴素贝叶斯模型(Naive Bayesian, N-B)收集考生特征属性，计算不同类别下的条件概率来预测期末的表现，最终提高预测的准确性。贝叶斯模型中各属性相互独立，但是在现实生活中，影响成绩的属性间往往具有紧密的联系，从而导致分类精度较差。上述文献分析证实了机器学习方法在某种程度上可以对考生的成绩进行有效的分析及预测，但仍然存在诸多缺陷。

虽然传统机器学习方法在EDM领域已较成熟，然而很少有将深度学习模型运用到成绩预测中。考虑到传统方法处理多元化非线性数据时效率较低，一批学者开始使用神经网络模型对考生成绩进行分析与预测。IBRAHIM等[8]利用人工神经网络，通过学生累计平均学分绩点(Cumulative Grade Point Average, CGPA)衡量其学业成绩。然而，该模型无法处理时间序列数据，因此未能考虑到前后成绩的相关性对结果的影响。OKUBO等[9]提出使用循环神经网络(Recurrent Neural Network, RNN)来预测学生期末成绩。该方法通过日志信息提取学生的学习活动，作为神经网络的输入。但是该方法忽略了考生个人信息,未能充分捕捉其特征。

为解决以上方法中存在的问题，本文将考生短期特征与长期特征相结合，提出一种新颖的多元特征感知的神经网络模型(Multiple Features-aware Neural Network, MFNN)。主要贡献有如下几点：

(1)本文将长短期记忆网络(Long Short Term Memory network, LSTM)应用到成绩预测中，利用该网络对考生进行建模。与经典的成绩预测方法相比，LSTM算法能提取出具有时序性的特征，从而提高预测结果的精度。

(2)针对传统算法无法感知多元特征的问题，提出MFNN模型。该模型利用LSTM模块和embedding模块同时捕捉考生短期特征和长期特征，从深度和广度两方面分析特征之间非线性关系。

(3)在2015年合肥市考生的真实数据集上进行大量实验，实验结果证明，本文提出的MFNN模型在理科和文科数据集上的预测精度均优于其他对比算法。

1 深度学习模型

本章主要介绍循环神经网络RNN以及长短期记忆网络LSTM。

1.1 RNN

循环神经网络[10-12]通过将当前神经元的隐藏状态传入下一时刻的神经元,使神经网络具备短期的“记忆功能”。设变长序列(x1,x2,…,xt)，RNN根据当前的输入xt以及上一时刻的隐含状态ht-1来产生下一时刻的输出Ot，一般ht直接用于输出,即ht=RNN(ht-1,xt)。

1.2 LSTM

长短期记忆网络[13-15]是为了解决RNN训练过程中梯度消失与梯度爆炸问题的一种优化网络结构。相比于RNN，LSTM能够更好地挖掘数据之间长期的依赖关系，是现今最为流行的一种方案。

如图1所示，LSTM模型包含3个控制门:遗忘门，输入门和输出门。

(1)遗忘门将上一阶段ht-1以及当前状态xt输入到sigmoid函数中，针对上一个神经元状态Ct-1进行选择性遗忘。遗忘门计算公式如下：

ft=σ(wtxt+ufht-1)。

(1)

式中：σ表示sigmoid函数，wt和uf表示遗忘门中的权值矩阵，遗忘门的输出为：

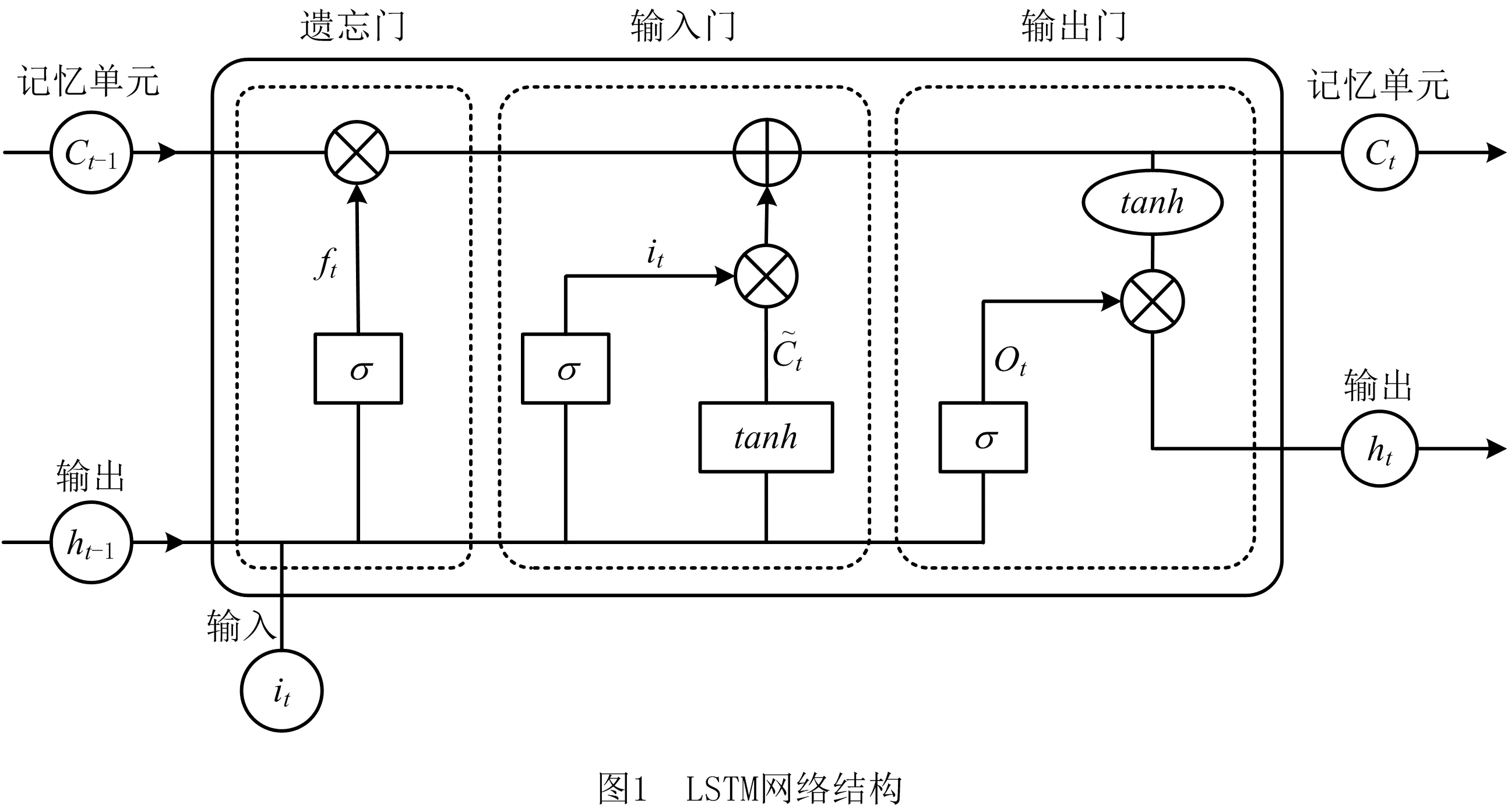
ft∘Ct-1。

(2)

式中：∘表示元素乘，定义如下：

A∘B=(a1,a2,…,an)∘(b1,b2,…,bn)=(a1b1,a2b2,…,anbn)。

(3)

(2)输入门通过上一状态的输出、当前状态的输入以及tanh激活函数生成候选新信息，得到下一时刻状态Ct，输入门计算公式如下：

it=σ(wixt+uiht-1),

(4)

(5)

(6)

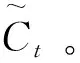
(3)输出门负责计算本层激活值。神经元的状态信息经过tanh层进行激活与Ot相乘，得到输出信息ht。输出门计算公式如下：

Ot=σ(woxt+uoht-1)。

(7)

式中：wo和uo是输出门中的权值矩阵，输出信息为:

ht=Ot∘tanh(Ct)。

(8)

2 多元特征感知的神经网络模型框架

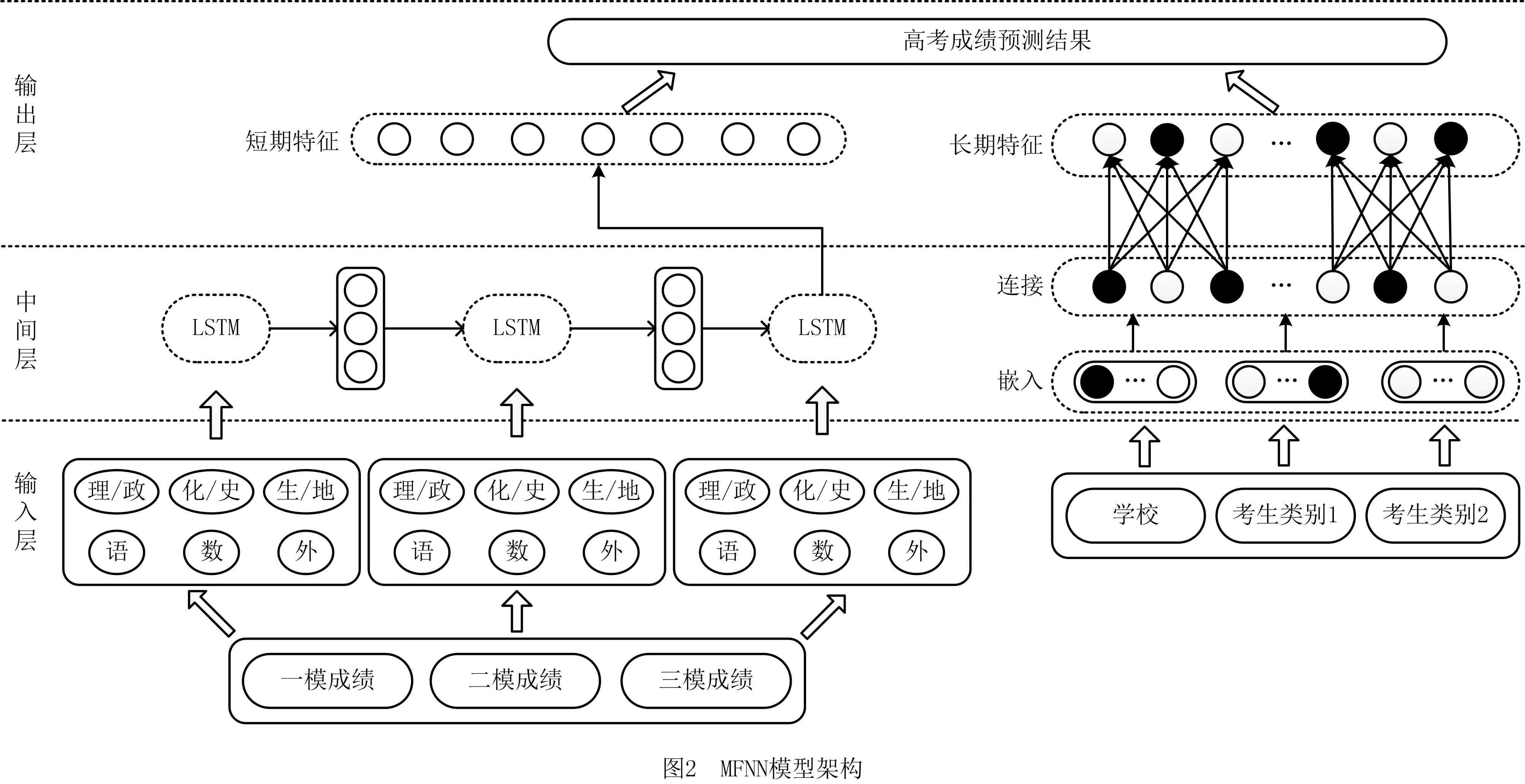
本章将详细阐述多元特征感知的神经网络模型MFNN，包括输入层、中间层和输出层，并介绍模型所使用的损失函数，MFNN模型架构如图2所示。

2.1 多元特征感知模型基本原理

2.1.1 输入层(Input Layer)

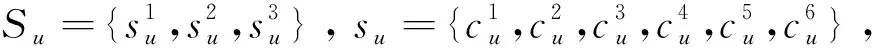
传统基于神经网络的预测方法，常利用考生u的成绩序列Su对u进行建模，仅捕获考生u近期学习状态，即短期特征Stu。为引入多元化特征，分析特征之间非线性关系，本文将u的个人信息Iu作为embedding模块的输入，捕获u的长期特征Ltu。

2.1.2 中间层(Middle Layer)

中间层主要包括两个模块：LSTM模块、embedding模块。中间层利用这两个模块同时从深度和广度两方面捕获考生u的长期特征Ltu和短期特征Stu。

(1)LSTM模块 LSTM利用神经元内部的门控机制选择性地保存序列以往的状态。因此，在获得具有时序性的输入Su后，LSTM模块利用记忆细胞学习u的短期特征，学习过程如下：

(9)

(10)

(11)

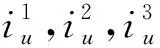
(12)

(13)

(14)

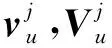
(15)

式中：C表示连接操作，Vu表示输出层所需的输入向量。

2.1.3 输出层(Output Layer)

输出层对Vu进行特征转换，得到考生u的长期特征，转换过程如下：

Ltu=fL(WL·Vu+bL)。

(16)

式中：fL表示激活函数，WL表示权值矩阵，bL表示偏置项。然后，输出层在考生u的长期特征Ltu和短期特征Stu的基础上，构建一个新的输出向量Gu。最后，通过一个全连接层，产生最终预测值。具体定义如下：

(17)

(18)

2.2 损失函数

MFNN模型预测考生u的高考成绩Ou，是一个回归问题。平方损失函数是一种常用于回归问题的Pointwise损失函数，具有以下3个优点：①避免正负误差不能相加的问题;②计算误差的过程中，提高对高误差的灵敏度;③一阶导数连续，容易优化。因此，本文使用平方损失函数优化MFNN模型。平方损失函数定义如下：

(19)

3 实验结果与分析

本章主要对实验结果进行分析，并对本文提出的MFNN模型的性能进行相关评价。首先介绍实验中使用的数据集，然后介绍评价指标和对比方法，最后通过不同参数的设置说明了本文提出的方法的研究价值与意义。

3.1 数据集描述

本文使用由合肥市教育局提供的真实数据集进行实验，该数据集由2015年合肥市高三考生3次模拟考试的成绩以及他们的高考成绩构成。为使实验结果更加准确可靠，需要对数据集进行预处理操作。将文科理科类型的考生进行分离，并去除了同一所学校相同姓名的考生记录。最终，数据集包含10 138名理工类考生以及4 874名文史类考生记录，每条考生记录包含22个特征属性值，分别是考生3次模考的成绩以及该考生的学校、家庭背景、考生类别以及高考成绩。

本部分实验环境是：Python 3.7 , JetBrainsPycharm 2018.1×64，Windows 7 , Intel i7-4790 CPU 3.60 GHZ处理器 , 4 GB RAM。

3.2 评价指标

为了评价MFNN模型的性能，本文通过命中率(HR)评估预测准确度并与其他方法进行对比。命中率的定义为：

(20)

式中：U表示测试集中考生集合,u表示U中的每位考生，R(u)表示根据训练集上特征预测出来的高考结果，T(u)表示测试集上的实际考试结果。

3.3 对比算法

为了验证MFNN模型在高考成绩预测方面的表现，将其与下列6种方法进行对比：

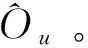
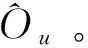
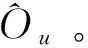
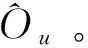
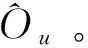
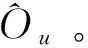
实验中，为了统一相关参数，设置神经网络的学习率为0.001，batch的大小为32，迭代次数为100次，优化器为Adam。其中，MLP、RNN、BiLSTM、MFNN的网络参数设置如表1所示。同时，为了消除实验结果的随机性，本文执行如下两种操作：①为获得更可靠的预测，按9:1,8:2,7:3,6:4的比例随机划分训练集和测试集进行多次实验;②在每个数据集上进行10次实验，取其平均值作为最终实验结果。

表2给出在不同数据集划分比例下7种预测方法的命中率，从表中可以看出，本文提出的MFNN模型具有最高的命中率。结果表明，MFNN总体上具有最佳的预测精度。因此，证明了同时考虑考生长期特征和短期特征的MFNN模型在成绩预测领域的有效性。

表1 网络参数设置

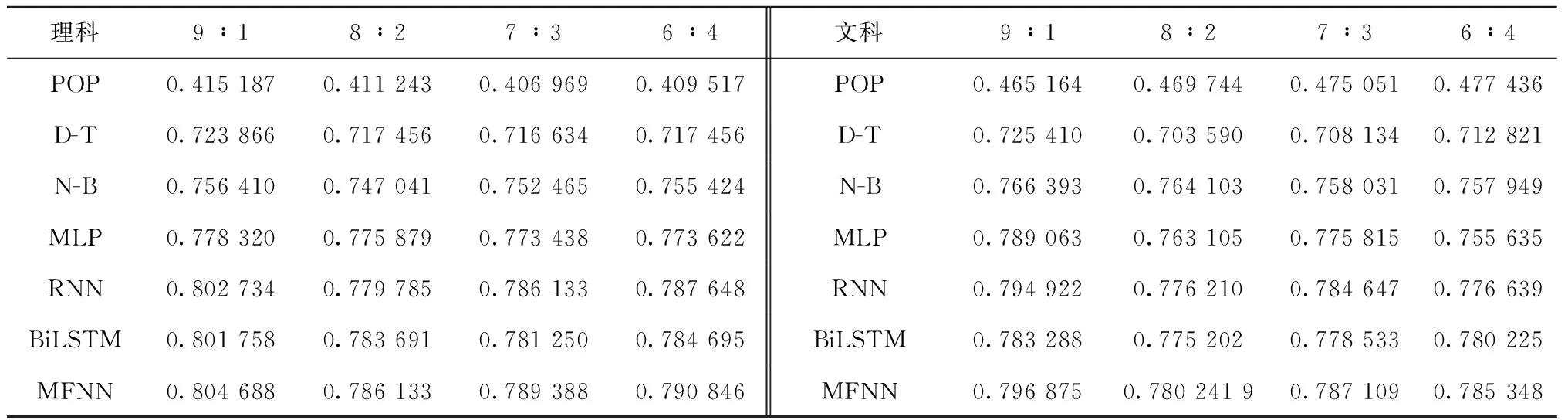
表2 预测性能对比

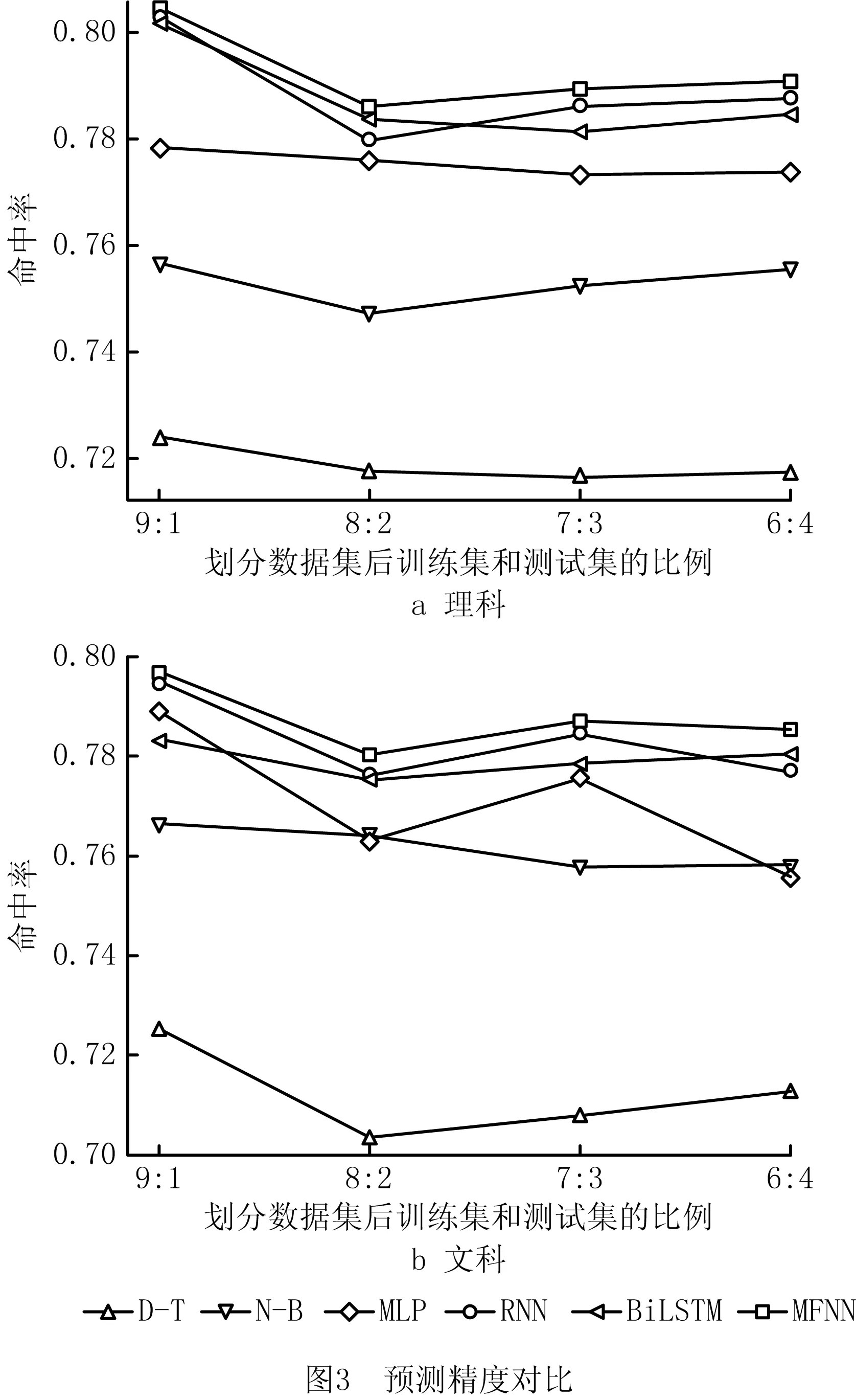
如图3所示为MFNN与其他5种方法命中率的对比结果(由于POP的性能较弱，省略了该方法)。由图3可以看出：①当训练集和测试集的比例为9∶1时，6种方法的命中率达到最高，意味着训练集有用信息足够时，可以学习出关键特征，从而使得预测精度提升；②基于神经网络的方法预测精度总体较高，这是由于神经网络具有强大的非线性拟合能力，能捕获考生更深层次的特征，因此使用神经网络能极大地提升预测精度；③基于RNN的模型较其他方法命中率更高，从而证明考生的短期特征对高考成绩具有一定程度的影响，其中BiLSTM的预测精度与RNN相似，说明在成绩预测中双向捕捉考生的特征意义不大；④MFNN利用RNN和MLP充分感知用户的多元特征，在6种方法中命中率最高。

3.4 参数对预测精度的影响

3.4.1 迭代次数

本文使用迭代次数λ来控制MFNN学习的进度。为了研究迭代次数λ对模型性能的影响，实验设置，λ的取值范围是1～100，步长为1，RNN、BiLSTM和MFNN的网络参数如表1所示。实验结果如图4所示。

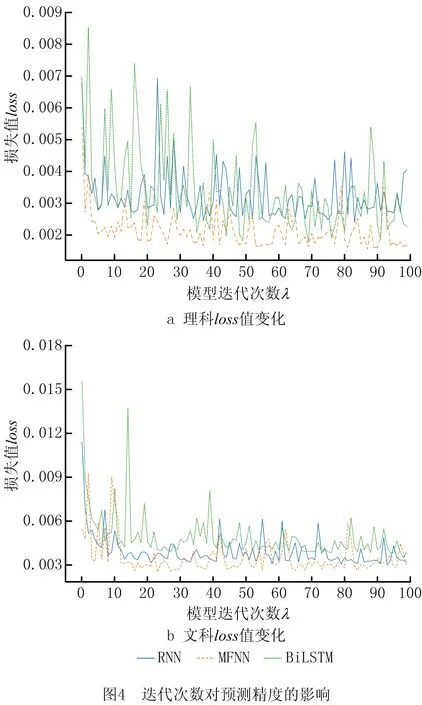
图4a和图4b分别显示在理科与文科中λ对损失值loss的影响。可以看出，当λ<10时，loss值下降迅速;当λ≥10时，loss值下降趋势变缓，逐渐收敛，这表明MFNN迭代10次后性能较为平稳，且理科loss值保持在0.004以下，文科loss值保持在0.006以下。此外，在100次迭代中，MFNN的loss值和loss值震荡幅度总体低于RNN和BiLSTM。证明MFNN引入考生的长期特征，能够更全面地对考生进行建模，提高预测精度和稳定度。

3.4.2 长短期特征维度

MFNN基于Ltu和Stu进行成绩预测，为了研究长期特征的维度LD和短期特征的维度SD对预测结果的影响，使用理科9:1以及文科7:3数据集进行实验。设置LD=[32,64,128,256]，SD=[8,16，32,64]，MFNN网络参数设置如表1所示，实验结果如表3和图5所示。

表3 长短期特征维度对预测精度的影响

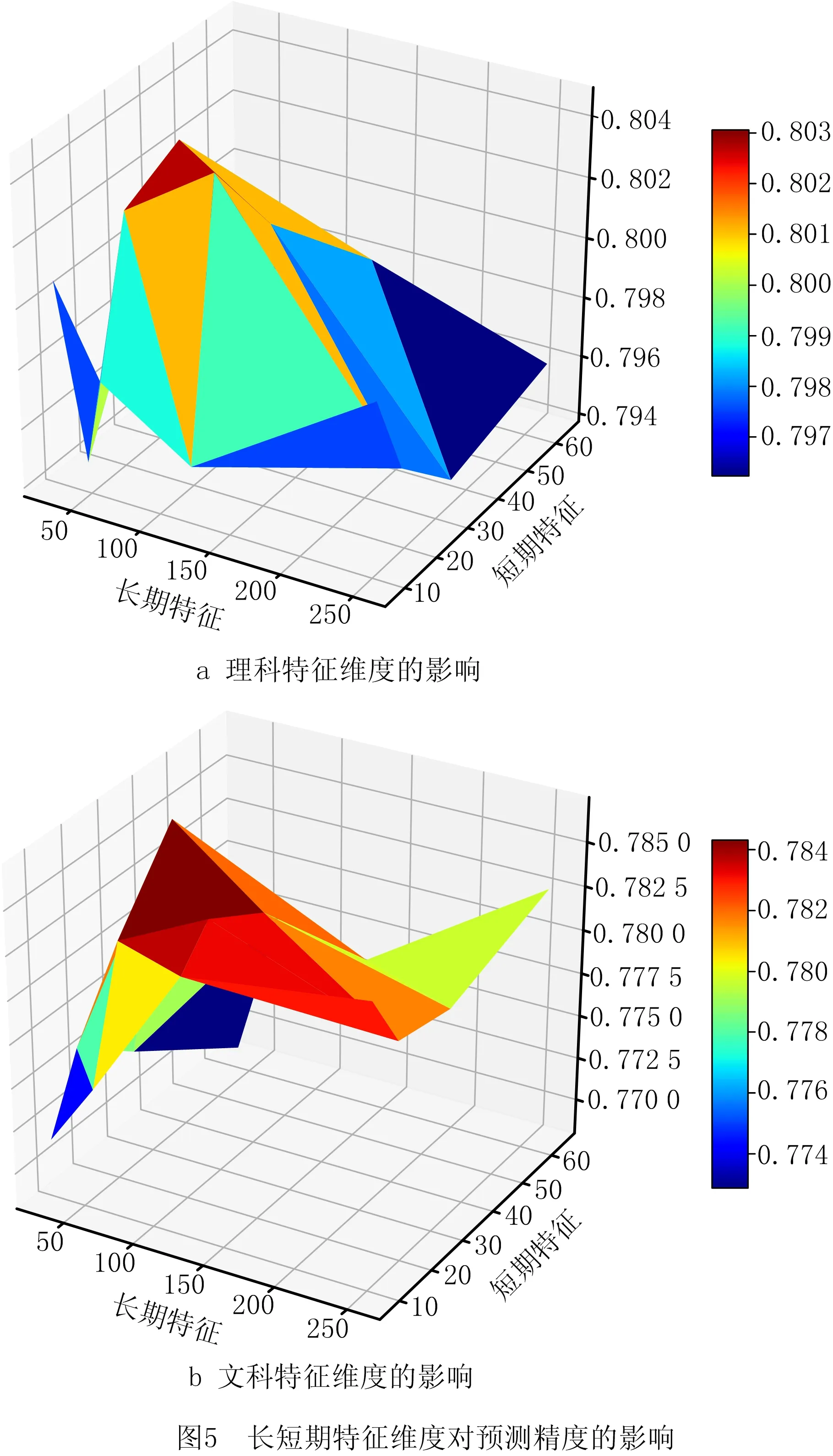
由图5及表3中可以看出维度LD和SD对MFNN的预测精度具有显著影响。维度过低，模型不能充分捕获考生特征；反之，模型将捕获其冗余特征，造成过拟合的现象。理科中当LD=16，SD=128；文科中当LD=32，SD=64，命中率达到最高。说明相比于长期特征，考生短期特征对高考成绩的影响更大，这一点在理科考生中尤为突出。

4 结束语

本文提出一种多元特征感知的神经网络模型MFNN，用于解决教育领域成绩预测的问题。该模型利用LSTM的记忆功能捕获考生短期特征，并将长期特征映射成嵌入向量来共同学习考生的多元化特征，综合考虑考生的短期特征和长期特征对高考成绩预测的影响。最后，在2015年高中质量检测与高考的真实数据集上进行了实验评估模型性能。实验结果表明，MFNN在预测效率上优于其他对比方法。未来将引入注意力机制到成绩预测中，并对艺体类考生的成绩进行相关预测与分析。