基于模型跟踪变结构算法的电子节气门控制

贾东明，张昊

（1.河南交通职业技术学院汽车学院，河南郑州450000；2.东南大学仪器科学与工程学院，江苏南京210000）

近年来，世界各国的汽车产销数量都在不断增长，日益增加的汽车产生的尾气排放问题对全球环境造成了极大压力。最早，节气门在汽车上的使用是采用机械连接的，也就是通过拉索将节气门和油门踏板连在了一起，当驾驶员踩下油门踏板时拉索便拉动节气门阀板打开，当驾驶员放开油门踏板时，在弹簧的回力作用下，节气门阀板关闭。这种联动方式简单直接却不利于精确控制，因此对汽车油耗的降低形成了桎梏。并且汽车只能被动地测量进气量来进行内燃机的转速控制，而不能通过节气门或者油门踏板的位置来主动参与控制，所以对行驶安全性也造成了一定影响。为了解决这一问题，伴随着电子技术的不断进步，国外的汽车零部件制造机构逐步将电子节气门应用到汽车上。电子节气门控制系统由油门踏板、电子节气门本体、电子控制单元（electronic control unit，ECU）等组成。驾驶员踩踏油门踏板时，并不会直接驱动节气门，而是先将踏板信息进行采集，输入到控制单元中，控制单元根据输入信息及预存在其中的控制算法来驱动节气门阀板打开并进行开度的精确控制。例如，当内燃机启动时，即使驾驶员还没有踩踏油门踏板，但出于怠速要求，节气门阀板必须已经打开一定角度从而保证初始进气量。这样，系统完全可以根据驾驶员意图以及内燃机实际工作情况来综合判断节气门电机的打开程度，而不是进行单一的跟踪式控制。

节气门阀板开闭的控制与汽车的排放控制是息息相关的。节气门一方面作为汽车发动机控制系统的关键部件，一方面又对内燃机的进气量及空燃比形成了影响。因此，节气门的控制精确程度影响到了进气系统控制、空燃比控制、废气再循环控制等，并最终对排放的控制形成了影响[1-2]。

PID控制作为控制领域应用最为广泛的控制算法，自然而然地被应用于电子节气门的控制，并成为了目前电子节气门控制中使用最多的算法。如果被控系统能够被准确建立数学模型，或者即使无法准确建模但系统不存在参数漂变，那使用PID算法也都是能够精确控制的。但对于电子节气门而言，很难准确建模，即使模型建立也可能会随着使用时间的增加而导致模型参数漂变，并且节气门在整个工作过程中难免会受到气流影响而产生扰动。从这些角度来讲，初期能够胜任控制精度要求的PID算法，其控制精度必然会随着汽车使用时间的增长而逐渐下降[3]。

近年来，众多国内外学者对电子节气门的控制算法进行了研究。有的针对PID算法进行了优化[3]，有的直接使用智能化算法进行控制[4-8]。本文针对电子节气门会随着时间推移而发生参数漂变、难以建立准确数学模型以及工作过程中存在各种扰动的情况，提出模型跟踪变结构算法，并与模型参考自适应算法的控制结果进行对比，得出了新算法响应速度快、鲁棒性强的特点。从而解决了建模不准、参数漂变、动态扰动所带来的种种问题。

1 电子节气门数学模型的建立

电子节气门数学模型的建立主要包括电机、复位弹簧、齿轮减速机构、阀片摩擦力矩等模型的建立。

1.1 电机模型

驱动电机数学模型的建立主要依据基尔霍夫电压定律进行确定：

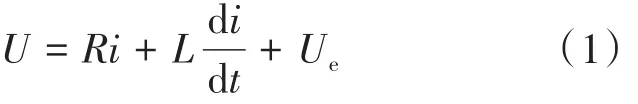
式中：R为电机的等效电阻；i为电机电枢通过的电流；L为线圈的等效电感；U为电机输入的电压；Ue为电机反向电压。

实际在电机的众多参数中电感数值比较小，通常可以忽略不计，所以式（1）可以简化为

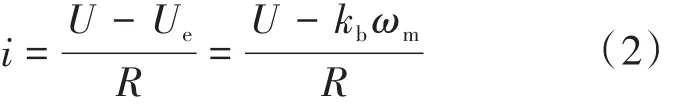
式中：kb为电机所产生的反向电动势常数；ωm为电机旋转的角速度。

从而可以得到电机转矩方程如下：

式中：k为电机的转矩系数；Bm为电机的阻尼系数；Jm为电机主轴的转动惯量；ω̇m为电机旋转时的角加速度。

1.2 复位弹簧模型

为了使电子节气门在初始的时候能够有一定的开度，所以在其中使用了两个弹簧，分别是开启弹簧和回位弹簧。当电子节气门阀板的转角θ大于初始位置转角θ0时，只有返回弹簧提供力矩来保证阀板返回θ0；当阀板转角θ小于初始位置转角θ0时，开启弹簧和回位弹簧同时提供相反方向的力矩，这时弹簧组的输出力矩就是两个弹簧的力矩之差。节气门所受的转矩为

式中：Ks为复位弹簧弹性系数；Tp为复位弹簧预紧力矩。

1.3 齿轮减速机构模型

电子节气门驱动电机输出为高转速低转矩，可以通过一组相互啮合的齿轮将动力转换为低转速高转矩。减速齿轮的传动比为

式中：ωt为电子节气门阀板转动的角速度。

1.4 摩擦力矩数学模型

电子节气门体中的摩擦力矩主要来源于黏性摩擦力矩Td和库仑摩擦力矩Tf。总摩擦力矩Tr就是这两种摩擦力矩之和，即

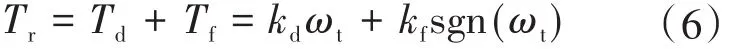
式中：kd为黏性摩擦系数；kf为库伦摩擦系数。

1.5 节气门执行机构的数学模型

电子节气门阀板是受到多个力矩的共同作用而进行运动的，主要包括以下三个力矩的作用：由直流电机所提供的驱动力矩Tm是最主要的力矩，由复位弹簧产生的弹簧力矩Ts以及节气门阀板在运动过程中所受到的总摩擦力矩Tr也参与其中。通过上述分析，可得出电子节气门执行器的动力学方程如下：

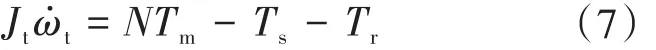
式中：Jt为节气门阀板轴的转动惯量；ω̇t为节气门阀板运动时的角加速度。

将式（3）～式（6）代入式（7）并进一步化简得到：

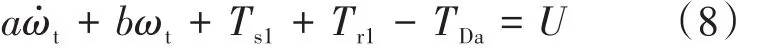
其中

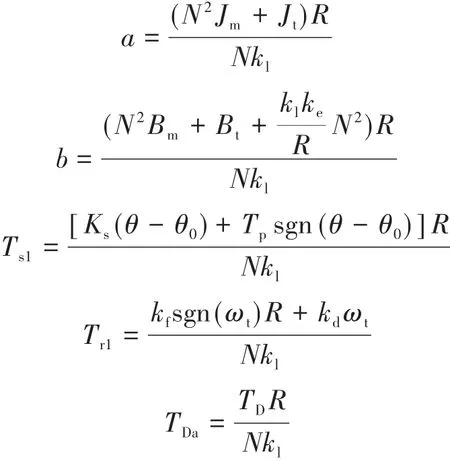
式中：kl为电机的转矩系数；ke为电机反向电动常数；Bt为节气门黏性阻尼系数；TD为系统内部干扰。

如果以节气门转动的角度θ作为变量，则可以得到一个二阶系统，其传递函数如下：

可将其转化成能控能观的状态方程如下：

代入具体数据之后可得：

2 目标模型的确定

为了使得电子节气门的控制性能可以满足要求，我们可以设定一个目标模型进行参考。如果最终控制的结果能够拟合所设定模型的控制过程，则节气门的控制结果也是令人满意的。通常为了满足拟合过程，所使用的算法是模型参考自适应算法，它将参考模型Gm（s）放至外环，可调节参数的算法与被控模型Gp（s）放至内环，以二者的输出差作为评判，致力于使得被控模型最终与参考模型相匹配。本文的目的是追踪参考模型的输出，而不纠结模型是否匹配。但无论是进行模型匹配还是进行模型跟踪，都需要有一个满足性能的模型。

由电子节气门的数学模型我们可以得知，现需要建立一个二阶系统的模型，且模型的各种性能均能符合我们的要求。

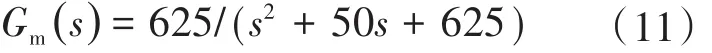
设定参考模型如下：转换成状态方程如下：

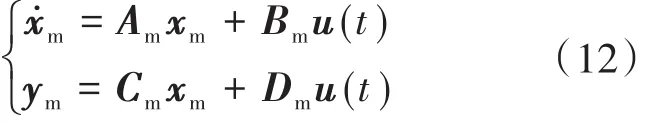
其中

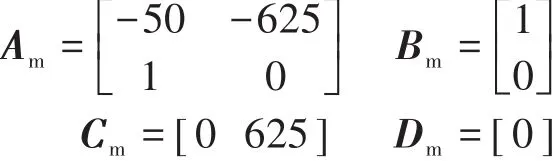
理想模型的正弦跟踪曲线及单位阶跃响应曲线如图1、图2所示。

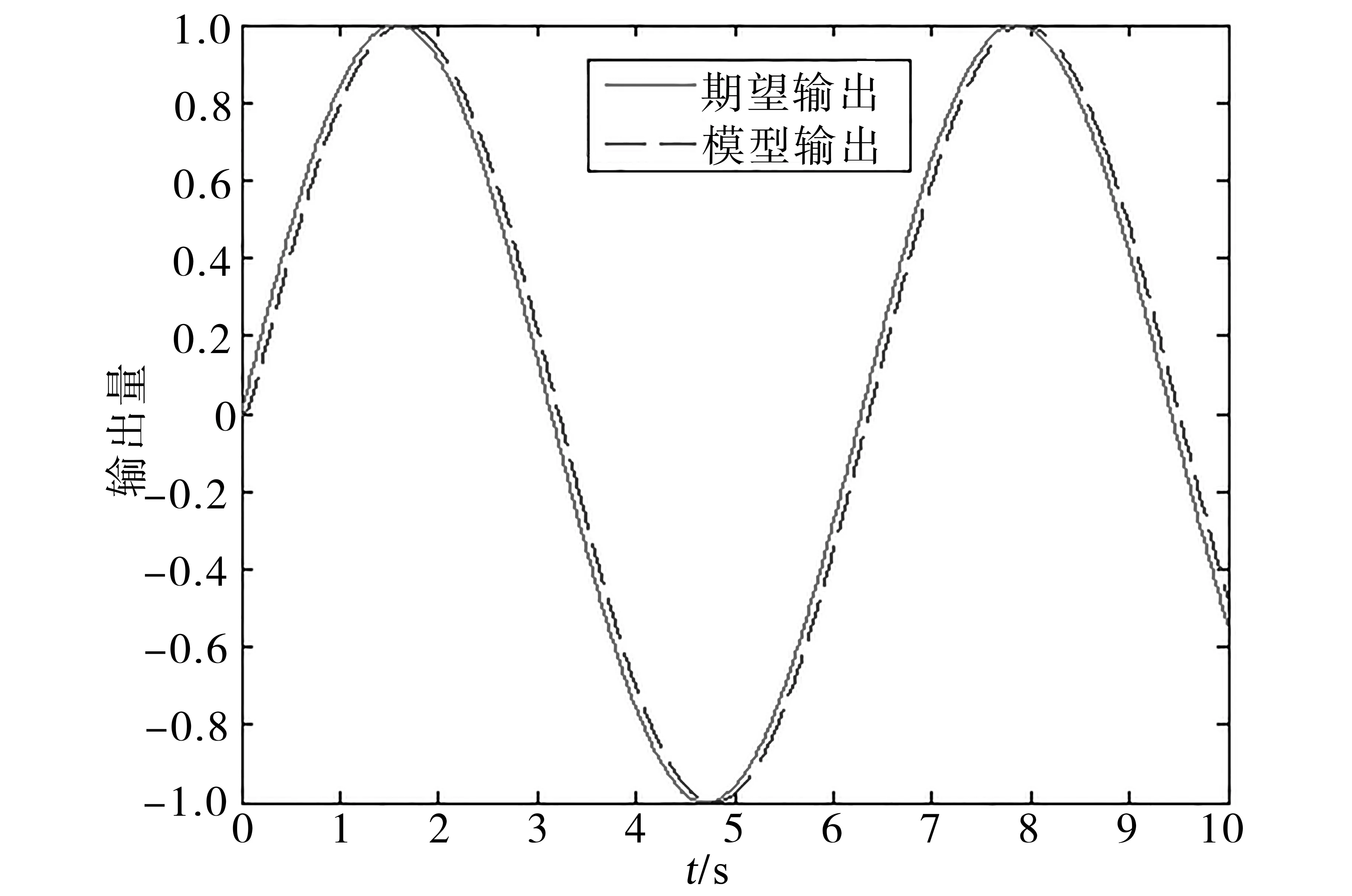
图1 理想模型的正弦跟踪曲线Fig.1 Sine tracing curves of ideal model

通过图1和图2可以看出，模型对正弦曲线的跟踪存在一定的滞后，但数值很小。模型对单位阶跃信号的响应曲线没有超调量，且0.3 s左右即跟踪上期望输出。因此所设定的参考模型能够满足需求。

图2 理想模型的单位阶跃响应曲线Fig.2 Unit step response curves of ideal model

3 模型参考自适应控制

模型参考自适应控制是进行模型匹配的有效算法。最早由麻省理工学院所提出的MIT控制律是基于局部参数最优化的方法。该方法比较直观并便于理解，但是却无法保证闭环系统的稳定性，从而使得其应用受到了限制。20世纪60年代中期由Butcharty和Parks相继提出的基于Lyapunov稳定理论的模型参考自适应控制，不仅使得系统稳定性得到了保障，而且相较于MIT自适应具有更快的控制速度。其控制的目的是使被控系统经调节后与模型趋于一致，从而最终实现参考模型输出的跟踪。

自适应控制在被控系统上加入可调节的前馈控制参数K1及反馈控制参数K2，由控制律与被控模型共同组成了下式：

如果被控对象参数已知，则只要满足下式：

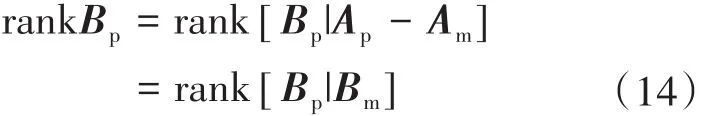
即可求解出参数，从而使得模型与被控对象完全匹配；如果被控对象参数未知或者是缓慢变化的，则可以通过某种非线性映射来调节参数K1和K2，最终使得下式成立：

从而使得下式成立：

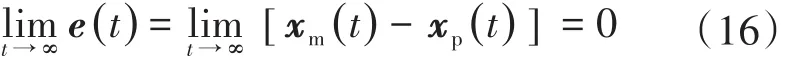
基于Lyapunov稳定理论的模型参考自适应控制，其控制律使用以下两式[9]：

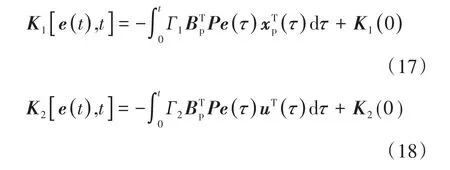
其中

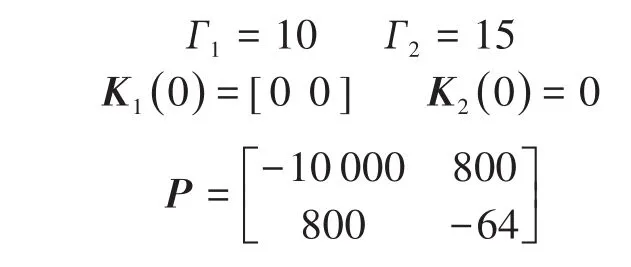
基于Lyapunov稳定理论的模型参考自适应控制对单位阶跃响应及正弦曲线的跟踪情况如图3、图4所示。算法的优点在于即使建模参数与模型参数不一致或者模型参数发生漂变也能应对，但是其初期的跟踪确实存在一定延迟，并且在进行单位阶跃响应跟踪时存在一定超调量，虽然不明显，但是在节气门控制中是应该尽量避免的。当然，对控制算法参数进行调节可以避免超调的产生，但却是以牺牲响应时间为代价的。

图3 模型参考自适应控制单位阶跃响应Fig.3 Unit step response of model reference adaptive control

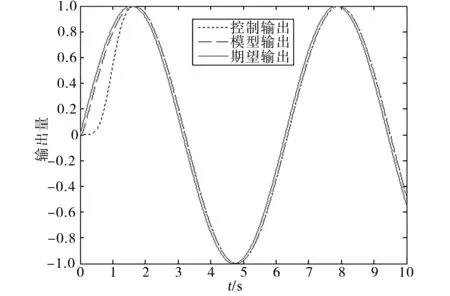
图4 模型参考自适应控制正弦跟踪曲线Fig.4 Sine tracking curves with model reference adaptive control

4 模型跟踪变结构算法

4.1 滑模变结构算法

滑模变结构算法是20世纪50年代所提出的一种可以应对非线性控制的简单有效方法。但滑模变结构算法在提出之初由于技术条件和控制手段的限制并没有得到广泛的关注。近年来，随着电脑控制速度的提升，此算法开始受到了广泛关注。特别是我国的控制专家高为炳院士提出了指数趋近律[10]，很大程度缓解了算法的高频振动，使得算法可以方便应用于实践。

滑模变结构控制算法需要寻求滑模面，当系统被控制到滑模面后，就会被吸附，从而沿着滑模面趋近到原点。因此，滑模变结构算法是大范围渐进稳定的。

4.2 模型匹配与模型跟踪的区分

为了说明本文所提出的算法，特将模型匹配与模型跟踪的结构绘至图5和图6。模型匹配算法是模型参考自适应控制的原理，其控制的基础是通过控制律来改变系统的前馈及反馈系数，从而使得控制后的被控对象与参考模型精确匹配。而模型跟踪的目的在于最终使得误差e趋向于零，而并不在乎模型与对象是否达到了完全一致。这种逻辑的优势在于设计之初就考虑到了如果系统存在扰动或者建模不准确的因素之后，仍然可以进行有效控制。所以系统可以不过多考虑参考模型本身的参数和结构，只对输出结果进行有效跟踪。为了配合此结构所具有的优势，在图6的控制律处使用适合非线性控制的滑模变结构控制算法。

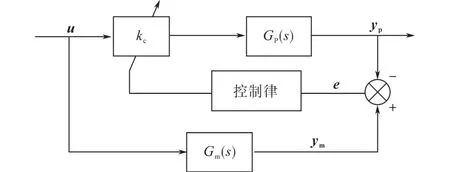
图5 模型匹配算法结构Fig.5 Structure of model matching algorithm

图6 模型跟踪算法结构Fig.6 Structure of model tracking algorithm

4.3 模型跟踪变结构算法

模型跟踪变结构算法在图6的控制律处使用积分滑模变结构控制算法。参考模型及被控系统采用式（12）、式（10）的状态空间表示法。

滑模函数如下式：

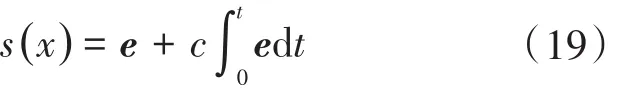
趋近律采用：

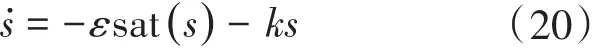
其中

式中：Δ为饱和层厚度。

控制律推导过程如下：

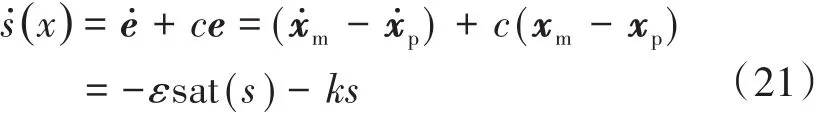
将模型及系统的状态方程代入得到：

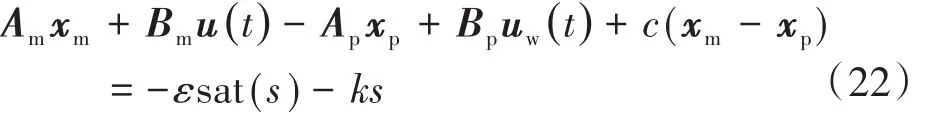
从而可以解出控制律：

4.4 模型跟踪变结构算法控制结果分析

图7和图8分别为模型跟踪算法单位阶跃响应和模型跟踪算法正弦跟踪曲线。

图7 模型跟踪算法单位阶跃响应Fig.7 Unit step response of model tracking algorithm

通过图7、图8与图3、图4对比可以得出，模型跟踪变结构算法在输出跟踪上的速度明显优于模型参考自适应控制，但是在最终的跟踪精度上不如模型参考自适应控制，这是由于本文所采用的趋近律所导致的。滑模算法在到达滑模面后会做高频的穿越抖动，虽然可以提升精度，但高频抖动会使节气门遭受损坏。算法中所使用到的饱和函数可以使系统到达滑模面后不做抖动，但却相当于把滑模面做成了一个有一定厚度的滑模曲面空间，从而对跟踪精度进行了妥协。这种妥协不仅在响应时间上得到了补偿，关键是在系统建模不准确时依然可以保障系统的稳定性。

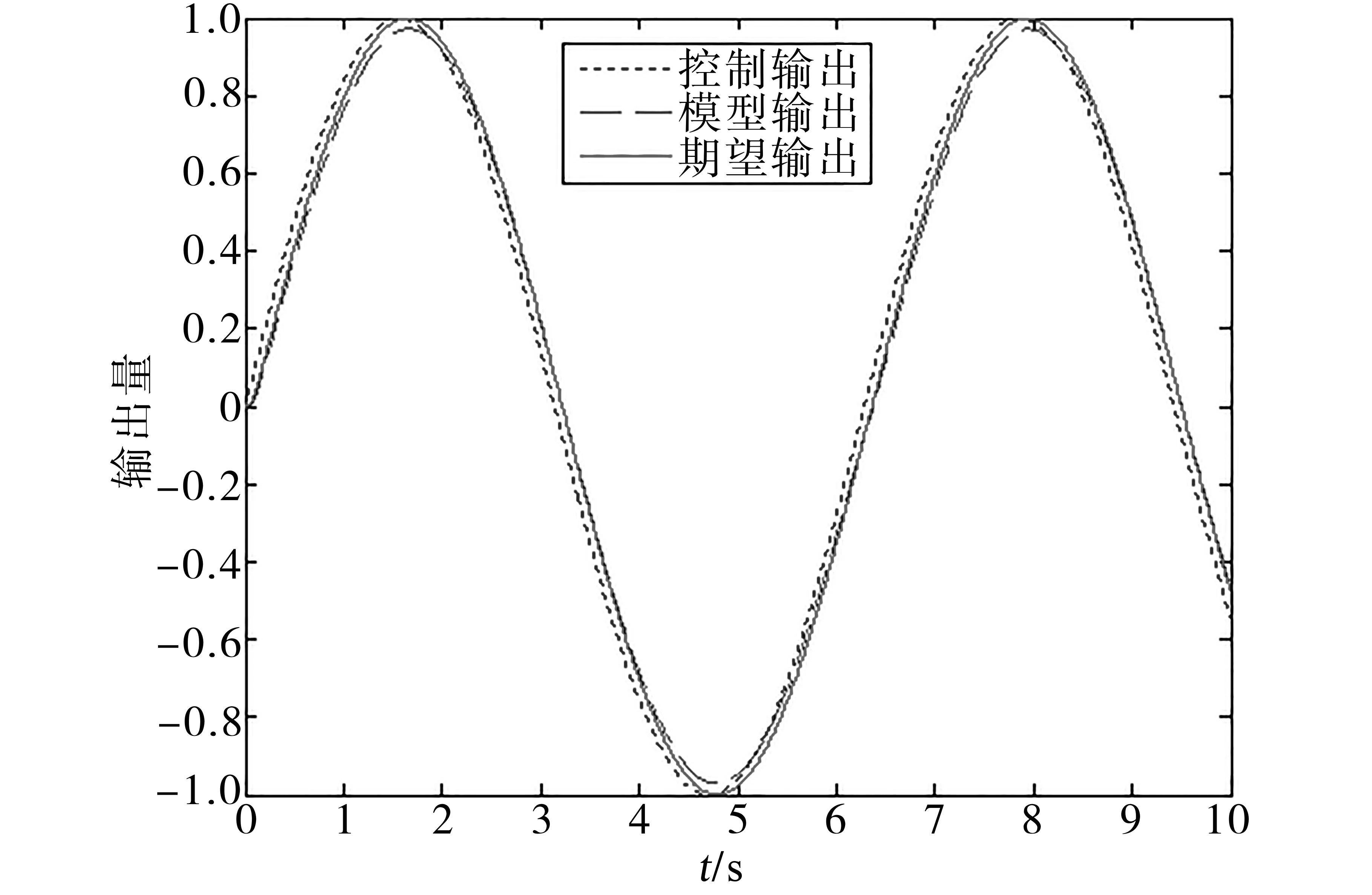
图8 模型跟踪算法正弦跟踪曲线Fig.8 Sine tracing curves of model tracing algorithm

4.5 模型跟踪变结构算法鲁棒性分析

模型参考自适应控制算法与模型跟踪变结构算法在系统参数发生漂变时都表现出了优良的适应性。但是当存在系统未建模扰动或各种非线性扰动时，模型跟踪变结构算法表现出了更为强大的鲁棒性能。

设Lyapunov函数为

采用式（20）的趋近律可知：s>0时，ṡ<0；s<0时，ṡ>0。因此得到：

所以滑模变结构算法滑模面的特点本身就保证了系统是稳定的。

20世纪80年代，Rohrs在研究Lyapunov模型参考自适应控制时发现，当系统受到扰动时，Lyapunov函数导数的半负定性就很难保障，所以系统就可能会失去稳定性，甚至连有界性也很难保障。为了使得算法更具代表性，本文使用Rohrs研究时所使用的模型及扰动函数。

图9～图12是使用两种算法来跟踪输入曲线r（t）时的跟踪误差，通过对比可以看出，模型参考自适应控制在极端情况下会导致输出误差不断增大，从而丧失稳定性。但模型跟踪算法在相同情况下却表现出了强大的鲁棒性能。

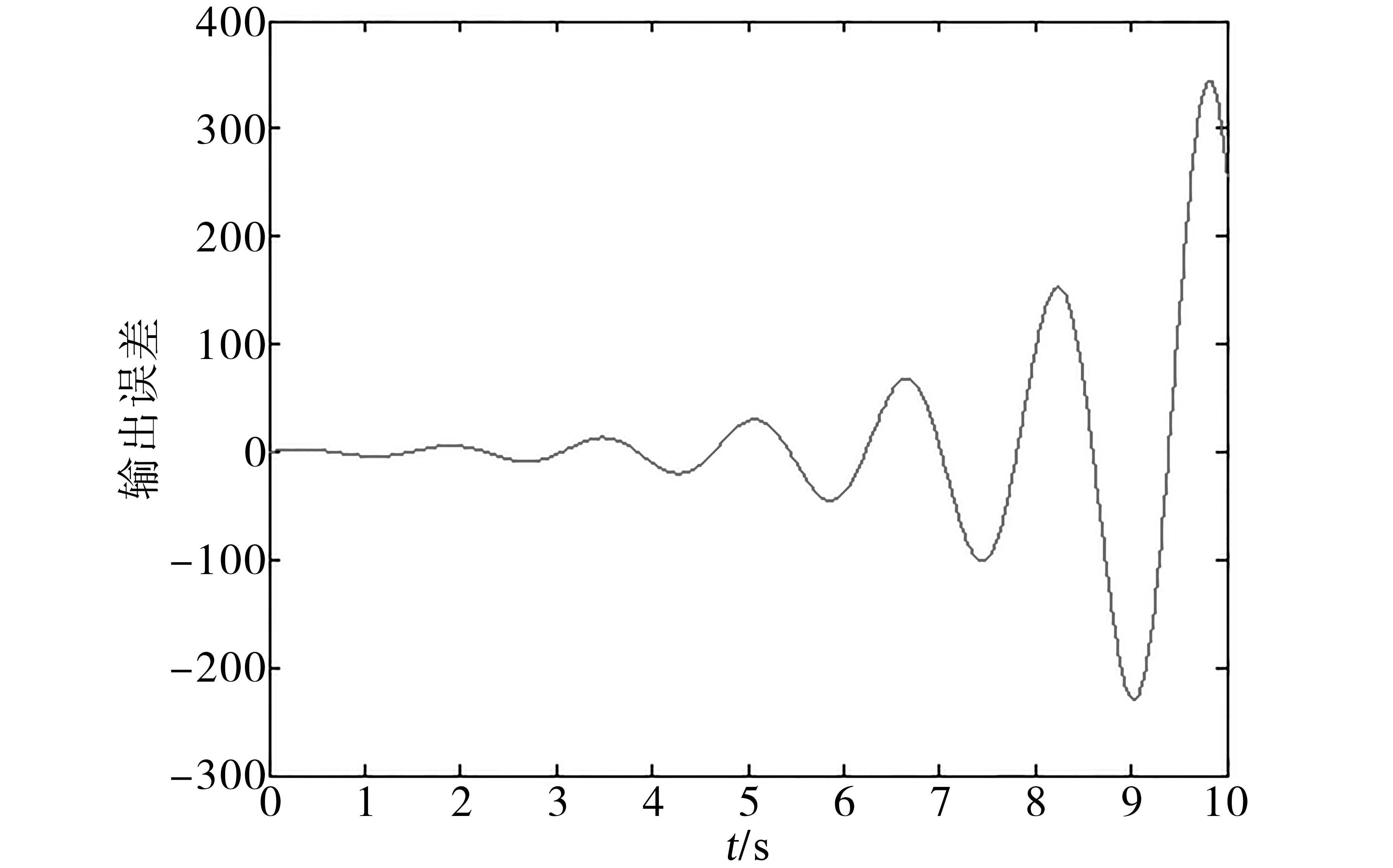
图9 模型参考自适应算法r（t）=4.3的误差曲线Fig.9 Error curve of model reference adaptive algorithm r（t）=4.3

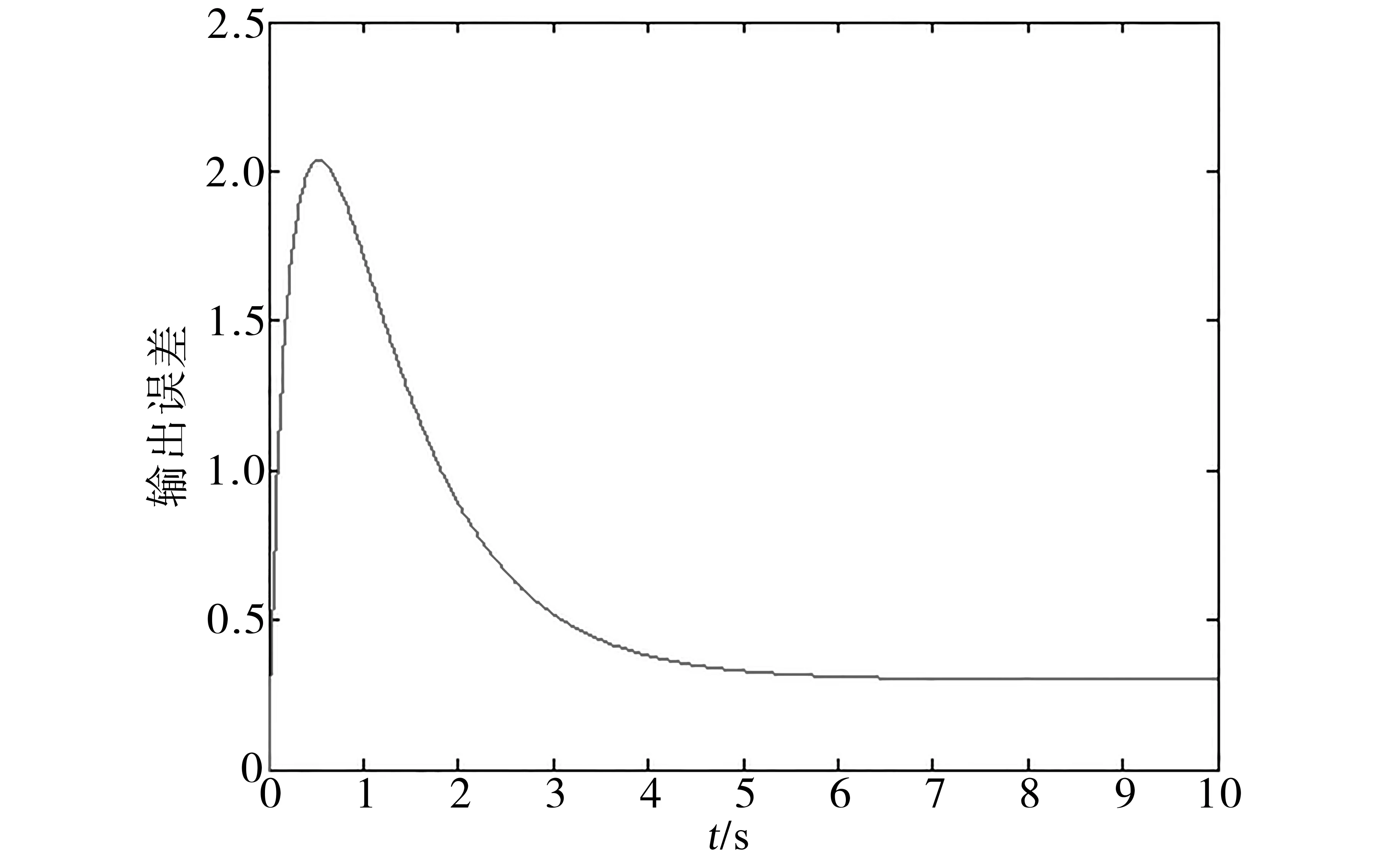
图10 模型跟踪算法r（t）=4.3的误差曲线Fig.10Error curve of model tracking algorithm r（t）=4.3

图11 模型参考自适应算法r（t）=1.8sin（16.1t）的误差曲线Fig.11 Error curve of model reference adaptive algorithm r（t）=1.8sin（16.1t）

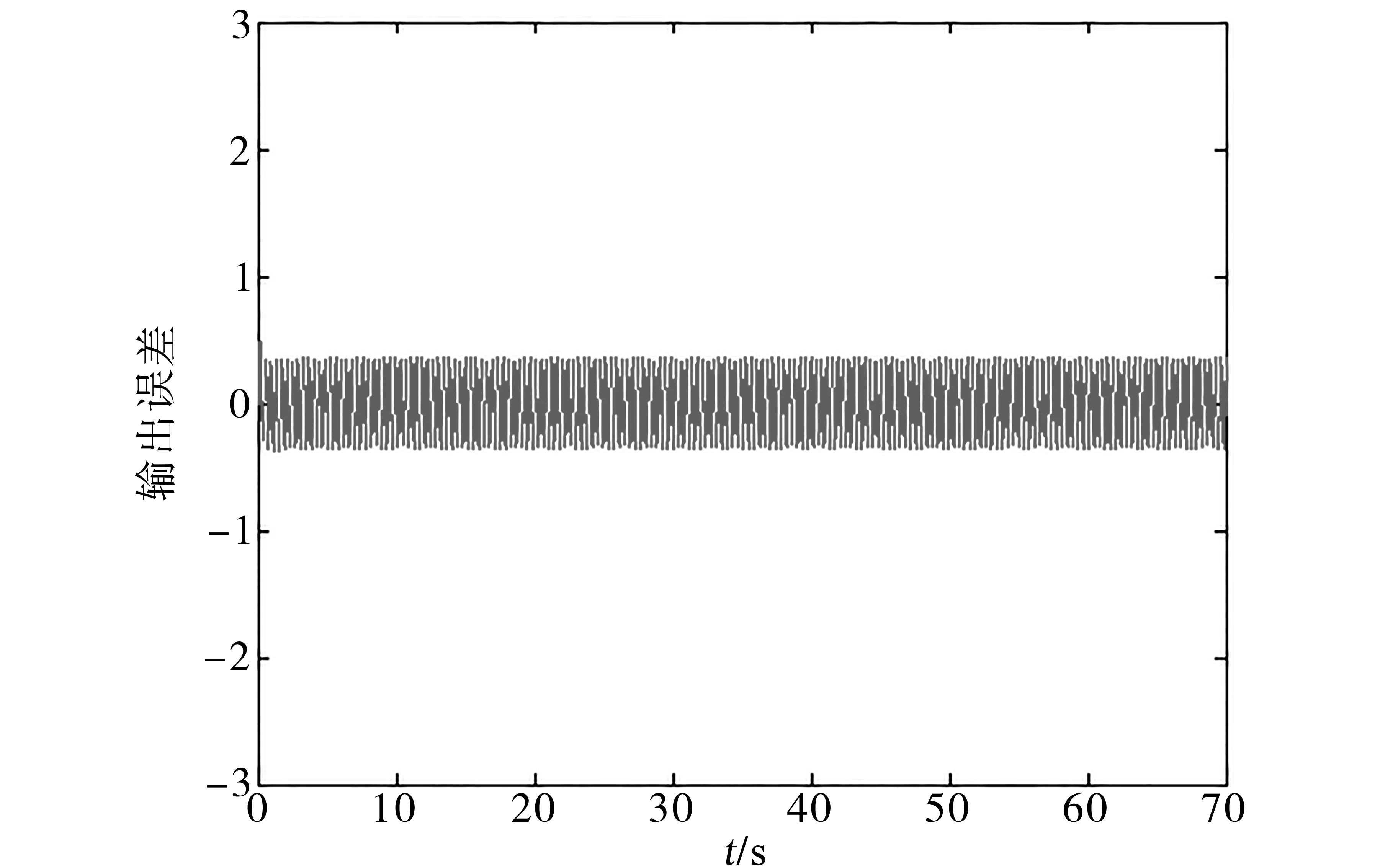
图12 模型跟踪算法r（t）=1.8sin（16.1t）的误差曲线Fig.12Error curve of model tracking algorithm r（t）=1.8sin（16.1t）

电子节气门工作过程中会受到高频气流扰动，为了研究算法的抗干扰能力，在系统中加入了高斯白噪声，其阶跃响应如图13所示。为了研究参数漂变对系统的影响，将被控对象式（9）的参数进行调整，使得：a1=1，a2=150，a3=3 000，b=6 000，其阶跃响应如图14所示。通过图13、图14可以看出，系统在受到扰动以及参数发生漂变时，依然能够得到理想的控制效果。

图13 模型跟踪算法在加入噪声后的响应Fig.13 Response of model tracking algorithm after adding noise

图14 模型跟踪算法在被控对象参数发生改变时的响应Fig.14 Response of model tracking algorithm when parameters changed

5 结论

本文针对目前电子节气门控制算法中存在的不能完美应对模型参数漂变的问题，提出了使用模型跟踪变结构算法进行控制的思路。首先建立了电子节气门的控制模型，使用基于Lyapunov的模型参考自适应算法进行了仿真。通过仿真可以看出，模型参考自适应算法在跟踪单位阶跃函数和正弦函数时均有一定的迟滞。

在模型参考自适应控制的原理基础上，提出了模型跟踪变结构控制算法，并进行仿真与模型参考自适应算法对比，得出模型跟踪变结构算法跟踪精度稍低，但跟踪延迟减小的结论。

为了将两种算法鲁棒性进行对比，本文采用经典模型及参数进行仿真，得出模型跟踪变结构算法具有较强鲁棒性的结论。因此，在电子节气门控制过程中，使用模型跟踪变结构算法以2%左右的稳态误差换取延迟的减少和鲁棒性的增强是合适的。最后，对系统加入噪声及参数漂变的情况进行了仿真研究，证明了模型跟踪变结构算法的有效性。