基于蒙特卡洛法的水电建设项目投资风险分析

冷建飞，陈心楠

(河海大学商学院，江苏 南京 211100)

目前，水电仍是我国可再生能源发电的主力，国家能源局发布的2020年全国电力工业统计数据显示，截至2020年，水电的发电设备容量为 37 016万kW，约占全口径发电设备容量的16.82%，仅次于火电，且较2019年同比增长了3.4%；水电发电量为13 552亿kW·h，约占全口径发电量的17.78%，仅次于火电，且较2019年同比增长了4.1%；水力发电新增设备容量为1 323万kW，较2019年同比增长了197.7%。由此可见，水电建设仍处于发展阶段，项目工程规模不断扩大，利益相关者也在逐步趋于多元化[1]，因此项目的投资风险分析也成了不可忽视的问题。

关于水电项目投资风险分析的方法，不同学者采用了不同的方法，王立等[2]运用敏感性分析对水利工程建设项目的不确定性进行了分析，这也是行业内部进行项目投资风险分析时最常用的方法；彭锟等[3]运用层次分析法结合模糊数学对巴基斯坦的水电工程项目进行了投资风险分析，该方法是许多学者在水电项目投资风险分析中广泛运用的方法，如张朝勇等[4]、谭唯薇等[5]、张乃平等[6]、陈思宇等[7]均在水电项目的投资风险分析中运用到了层次分析法；此外，钟登华等[8]、吴业鹏等[9]、陆路等[10]分别运用网络分析法、基于熵权法的灰色关联模型、群组决策对水电项目进行了投资风险分析；张云宁等[11]运用了云物元理论和结构方程模型(SEM)，构建了水利工程BIM应用效益评价模型；陈国梁等[12]利用D-S证据理论，建立了水利水电项目投资风险评估模型。

上述方法中，敏感性分析虽然在业内较为常用，但其只能看出单个敏感性因素对项目净现值产生的影响，无法综合反映各个因素共同作用时对项目净现值产生的影响。层次分析法的使用前提是各层次中的风险因素是相互独立的，但在实际中各风险因素都或多或少存在一定的关联性。网络分析法能较好地解决层次分析法这一使用局限性，能有效地分析各风险因素之间的关系并找到关键因素，但其评价指标体系繁杂，不同项目的评分权重都存在差异，实际实施起来比较复杂。群组决策、D-S证据理论等方法中的许多风险因素的评分都是由专家评估的，存在一定的主观性，使得风险分析的结果可能存在误差。而蒙特卡洛(Monte Carlo)法能较好地解决上述问题，它不仅不受因素关联性的影响，还可以将多个因素的共同影响综合反映出来，而且作为一种随机抽样的仿真模拟，能从最大程度上减少人为评分的主观影响，使结果更加客观。同时，大量的随机抽样，也使得结果更加接近真实值。

1 蒙特卡洛法

1.1 基本原理

蒙特卡洛法是一类通过随机变量的统计试验、随机模拟，求解数学物理、工程技术问题近似解的数值方法[13]。该方法的基本思想是：已知目标函数y=f(x1，x2，…，xn)，并对随机变量(x1，x2，…，xn)作概率分布估计，对这些变量进行随机抽样得到对应的目标函数y的特征值，通过多次抽样计算获得y的概率分布。抽样模拟次数越多，模拟结果与实际情况越相近，蒙特卡洛模拟法的计算精度越高[14]。

1.2 计算步骤

运用蒙特卡洛法进行项目风险分析的一般步骤为：①根据所需分析的问题构建模型；②识别风险变量，并确定风险变量的概率分布；③对风险变量进行大量充分的随机抽样，并根据模型设定的函数关系得到目标函数的对应值；④对得到的所有目标函数值进行统计学处理，得到期望值、标准差、概率分布、累计概率分布等统计特征，并据此对项目进行风险分析。

2 模型构建

本文关于衡量项目投资风险的指标选取参考王核成等[15]的方法，选择净现值(NPV)作为衡量项目投资风险的指标，净现值(NPV)的计算公式如下：

(1)

式中：NPV为净现值；NCFt为第t年的净现金流量；CI为项目的现金流入；CO为项目的现金流出；n为项目经营期；ic为项目的贴现率；I为项目的初始投资额。

3 实证分析

3.1 项目概况

国内某水电站建设项目的装机容量为392 MW，单独运行时，多年平均年发电量14.83亿kW·h；与上游水库联合运行时，多年平均年发电量 17.29亿kW·h(将增加的50%的电量效益返还给上游水库电站)。按2019年1季度价格水平，该水电站静态总投资为407 746.09万元，计入价差预备费 21 901.82万元，固定资产投资为429 647.91万元，项目投资财务内部收益率采用8%，计算期采用 30年，在本文的模拟中，假设项目的总投资额在初期一次性投入，分别对该水电站单独运行和联合上游水库运行时的情况进行模拟。

3.2 项目投资风险变量分布

影响水电建设项目净现值的主要风险变量有：上网电量、上网电价、经营成本和初始固定资产投资。根据专家评估和历史数据可得出各风险变量的分布如表1所示。

表1 风险变量分布

3.3 蒙特卡洛模拟及敏感性分析

利用Crystal Ball对该水电站单独运行和联合上游水库运行时分别进行蒙特卡洛模拟，图1、表2～4显示进行了20 000次蒙特卡洛模拟后的试验结果。

图1为Crystal Ball模拟所得的净现值预测值频率分布图截图，(a)、(b)分别为该水电站单独运行和联合上游水库运行时的净现值预测值频率分布图截图，图中的频率代表模拟过程中所得净现值对应的发生次数，概率代表模拟所得净现值对应发生次数占总实验次数的比率，确定性代表净现值大于0发生的概率，绿色曲线为基于Beta分布的模型拟合优度检验。由图1可知，该模型拟合情况较好。该水电项目单独运行时，净现值大于0的概率约为73.63%；联合上游水库运行时，净现值大于0的概率约为87.81%。显然，该水电站联合上游水库运行比单独运行的项目投资风险要小。

表2为净现值的统计表，可以更为直观地看出图1中净现值的均值、最大值、最小值、平均标准误差等统计数据。由表2可知，该水电项目单独运行时，项目净现值均值为4.41亿元，且在4.41±0.05亿元的范围内波动，最小值为-11.18亿元，最大值为25.20亿元；该水电项目联合上游水库运行时，项目净现值均值为7.30亿元，且在7.30±0.04亿元的范围内波动，最小值为-8.46亿元，最大值为27.49亿元。由此可见，无论是均值、最小值还是最大值，该项目联合上游水库运行时的表现均优于单独运行。

(a)单独运行

表2 净现值统计

表3为净现值的百分点表，百分点的数值是基于20 000次仿真模拟所产生的净现值，将其由小到大排列，并获取每10%的最后一个数值所得，可以更为直观地看出图1所得净现值每个百分点的情况并进行对比。由表3可知，该项目各个百分点的数值均为联合上游水库运行大于单独运行，表明该项目联合上游水库运行的收益表现优于单独运行。

表3 净现值百分点

表4为影响净现值的各风险变量的敏感度贡献表，由表4可知，无论是单独运行还是联合上游水库运行，上网电价和上网电量均是对净现值影响最大的两个变量，初始固定资产投资和经营成本对净现值的影响很小。

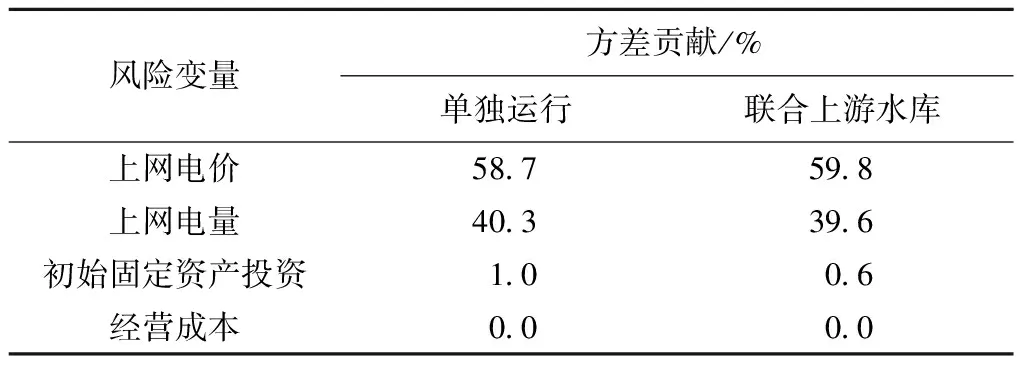
表4 敏感度贡献

3.4 联合发电延后实现的蒙特卡洛模拟

由于该项目实际上实现与上游水库联合发电并不是项目建成的同时就能实现的，而是在项目建成后的第4年实现的，这可能会对项目的投资风险和收益产生一定的影响，所以需进一步探究与上游水库联合发电的延后实现对项目投资风险和收益的影响。继续运用蒙特卡洛法分别对联合发电的实现时间延后1～30年进行20 000次仿真模拟，得到的试验结果如图2、图3所示。

图2 NPV大于0的概率变化

图3 净现值极值及均值变化

图2为联合发电的实现时间延后1～30年时，通过仿真模拟所得的净现值大于0的概率变化图。由图2可知，当该项目联合发电的实现时间延后 1～5年时，该项目净现值大于0的概率是在不断上升的，第6年开始，该项目净现值大于0的概率开始持续下降，即该项目联合发电的实现时间延后5年的投资风险是最小的。而当延后时间大于等于12年时，该项目净现值大于0的概率开始低于无延后(项目建成的同时就实现联合发电)的概率，即延后时间超过12年的投资风险是高于无延后联合发电的。综合来看，该项目的投资风险随着实现联合发电延后年限的增加，呈现先下降后上升的趋势，但无论延后多久，该项目联合发电的投资风险是始终低于单独运行发电的。而本项目的基本运行方案，即在项目建成后的第4年实现与上游水库联合发电是投资风险较小的。

图3为联合发电的实现时间延后1～30年时，通过仿真模拟所得的净现值的均值及极值变化图。由图3可知，随着项目实现联合发电延后年限的增加，净现值的均值是在不断下降的，最大值和最小值总体也呈现下降趋势，说明该项目的收益是在不断下降的，所以联合发电实现的时间越长，收益越高。

4 结 语

通过蒙特卡洛模拟对项目的净现值进行仿真模拟，对比分析了该水电项目单独运行和联合上游水库运行时的投资风险差异，以及与上游水库联合发电的延后实现对项目投资风险的影响。蒙特卡洛模拟能较为直观综合地反映出多个因素共同作用时对水电建设项目投资风险的影响，可为水电项目建设企业和投资者分析项目投资风险提供参考；此外，除了上网电价和上网电量是影响水电建设项目投资风险的关键因素，该水电建设项目是否联合上游水库发电，以及与上游水库联合发电的延后实现也会对项目投资风险产生一定的影响。据此，建议水电项目建设企业要注意善用梯级流域建设水电站，多利用上游水库联合发电，提升水电站的发电效率，合理安排好项目建成和实现联合发电的预期时间，力求风险最小化和收益最大化；投资者应重点关注资金的使用流向，若项目是以联合上游水库发电为基本运行方案的，要注意实现联合发电的时间，若存在一定的延后性，要注意延后年限的长短对项目投资风险和收益的影响。