浅谈初中数学章节复习课的有效性——以圆的基本性质复习为例

俞 燕

(青田县章旦中学教育集团 浙江丽水 323900)

在复习阶段，笔者经常思考如何上好一堂复习课，怎样复习才是有效的复习。因此，以圆的基本性质这一章为例，尝试实践复习课的上课方式，反思在教学中存在的不足，并为后续复习课提供思路。

一、如何上好一节复习课

在数学教学过程中，存在两种比较常见的复习课状态。第一种习题课。这种课堂对学生来说只是一堂解题课，一节课在解题和校对中度过，对于学生而言原来会的还是会，原来不会的现在仍是模模糊糊。他们对本章知识的脉络是不清晰的，知识点是分散的。另一种比较常见的是将复习课转变成专题课。当然专题复习有其优越性，但它达不到梳理整章知识点的目的，因此也达不到课堂真正的有效性[1]。

在我看来，好的复习课首先应促进学生形成知识点网状结构，找寻每个知识点的联系和转化。其次，应是一个查漏补缺的机会，使学生在本章新课学习后作业中所暴露的问题得到有效解决。其三，要借机提升，综合解决问题。

二、圆的基本性质教学过程

（一）视频引入，导出主角

在课前花2分钟时间先抓住学生眼球，用一个动画《圆滚滚的动物世界》这一短视频引出——“圆”这一主角。动画中的动物都是圆滚滚的，一个个憨态可掬的形象，以此来达成圆是世界上最完美的图形之一的认知。帮助我打破借班上课的尴尬局面，拉近我与学生之间的距离。

（二）梳理知识脉络

教师先用几何画板给出圆这一图形，并画一条直径。

教师：观察这一图形你看出圆的什么性质了？

生：轴对称性，圆是轴对称图形。

教师：有此图，你会联想到什么？

生1：垂径定理。加一条弦和AB垂直。

教师：给出图形。如图1，在⊙O中，直径AB⊥弦CD于点E，OE=3，CD=8，求圆的半径。

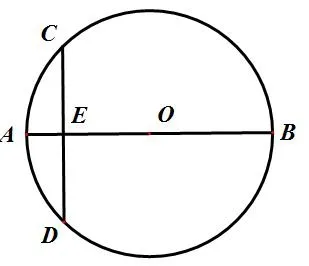
图 1

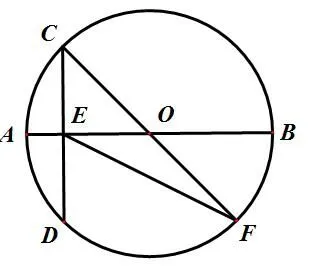
图 2

生2：连接OC，根据直径AB⊥弦CD，得CE=ED=4（垂径定理），根据勾股定理可得圆的半径等于5。

教师追问：解题依据？生2：利用垂径定理。师生共同回顾垂径定理的相关内容，并将数学文字语言转化为几何语言。

变式1：如图1，若已知直径AB平分弦CD于点E，CD=8，AB=10，试求OE的长度。

生3：利用垂径定理逆定理以及通过设未知数，结合勾股定理来解决此题。

在三小题的转变中，通过稍动已知条件，总结回复知识点并达成灵活应用。三位学生的回答将直径、弦、半径三者之间构成一条线。

变式2：如图2，若已知直径AB平分弦CD于点E，CD=8，AB=10，延长CO，交圆O于点F，连接EF，试求EF的长度。

此题考查的是垂径定理的逆定理，以及在圆中利用垂径定理及其逆定理求解线段长度的问题。圆中隐含条件的利用往往是解题的关键。此题即是利用直径所对的圆周角是直角结合勾股定理帮助解决，师生回顾知识点并总结方法。

教师：再次利用此图，老师稍加改动，继续探究。

如图3，若已知直径AB平分弦CD于点E，连接AD，OD。若已知∠COA=40°，求∠DOA，∠ADC的度数。

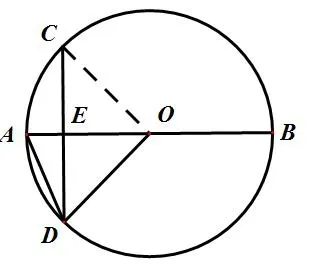
图 3

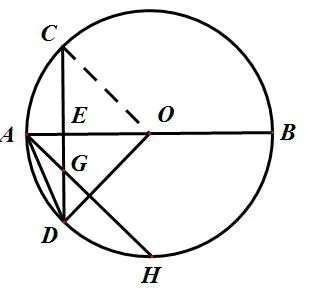
图 4

生4：根据垂径定理可知有弧AC等于弧AD，则弧对应的圆心角相等，又因为同弧所对的圆周角等于圆心角的一半，∠DOA=40°，∠ADC=20°。

教师：要求圆心角或圆周角我们往往会将角转化到弧，借助弧来求角，在板书上将圆心角、圆周角与垂径定理相连。

变式：如图4，AB是半圆O的直径，D是AH的中点，CD⊥AB于E，交AH于G，求证：AG=DG。

生5：要求AG=DG，证明这个三角形是等腰三角形，我们只需证明∠GAD=∠ADG，要证这两个角相等转换到弧，即可求证。

此题考查学生对圆心角圆周角的理解及应用，并借助于题目将圆心角、圆周角、弦（直径）和弧之间的关系理清。在解决此类相关问题时，学生需要灵活转化。

（三）拓展应用（走进中考）

如图5，点A，B，C，D，E均在圆O上，∠BAC=15°，∠CED=30°，则∠BOD的度数为 。

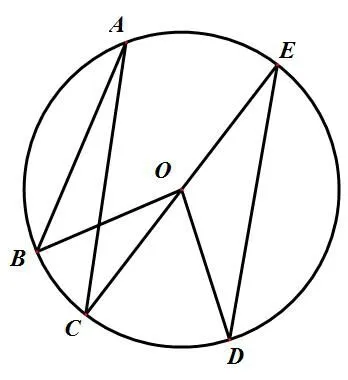
图 5

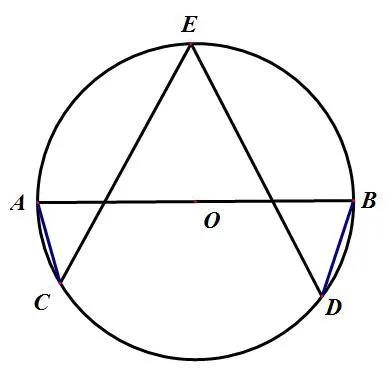
图 6

生6：∠BOD=∠BOC+∠COD。转到弧BC和弧CD，再将其转化到相对应的圆周角。

变式：如图6，AB是圆O的直径，点C，D，E都在圆O上，若∠C=∠D=∠E，则∠A+∠B=________。

此题学生并不能很灵活的转化，对于角到弧的转化运用不够熟练。教师给予提示。

弧与角之间的转化，学生在处理此类问题时，存在混乱，找不到对应的入手点，两题的训练旨在帮助学生感受角到对应弧的转变，并总结规律。在求圆中角度问题，往往先找到角所对应的弧。

（四）综合运用

如图7，△ABC内接于圆O，AB为圆O的直径，AB=10，AC=6，连结OC，弦AD分别交OC，BC于点E，F，其中点E是AD的中点。

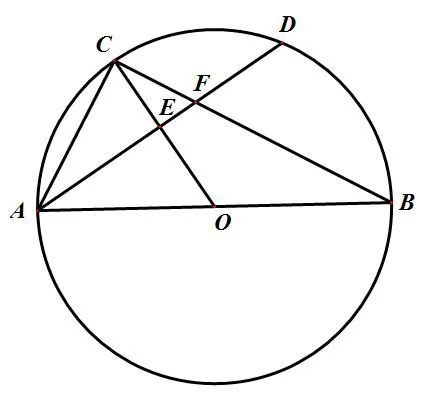
图7

（1）求证：∠CAD=∠CBA。

（2）求OE的长。

综合题的运用，是检测学生对于知识点掌握的重要手段之一。将圆中的知识点做一个整体的梳理，并通过此题让学生感受弦、圆心角、圆周角直接的转化。在求解线段长度问题，我们往往将其转化到特殊的三角形中，构建模型，构建方式方法。

（五）知识梳理

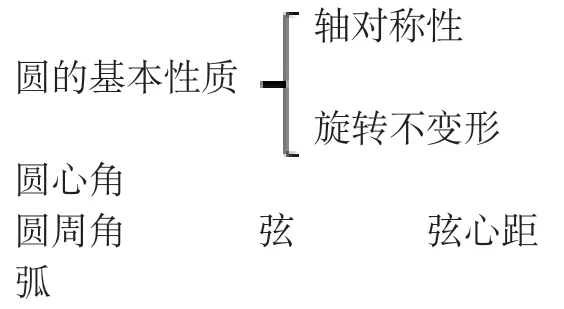
三、课堂教学反思

复习课与新授课存在的区别在于如何将无序的转化为有序的，从点状到网络状思维的转化。本节课虽已进入尾声，但教学的反思之路不停，值得思考的地方仍有很多。

（一）变式训练

在复习课过程中变式可以为突破知识点，以及检测学生对于此类问题是否掌握起到关键作用。本节课有三处变式训练的设置，分别来达到垂径定理、圆心角圆周角和弧与角知识点的落实。

在实际课堂实施过程中发现，变式题设置的难度分层并未体现。例如在垂径定理复习环节，三个变式的难度其实是在同一层次上的。垂径定理这一块内容在中考题是一个必考点，在近几年丽水卷中垂径定理往往以证明题一道大题的第一小问出现体现。因此在课下，我想对于垂径定理复习是否可以由此在此题复习后让学生真实感受中考题，清晰考点以及不惧怕中考。

在圆心角圆周角复习过程是采用中考题来体现的，两题之间的关联也比较密切，转变方向再次思考，但此题后续的数学思想体现还不够，在教学过程中可引导学生举一反三，转化思想。

（二）一题一课

有幸在培训过程中看到过温州优秀名师的一题一课教学，将一节课以一种串联的方式，层层深入，由浅入深。在代数式中通过改变数字，图形中通过加线条的方式来完成一节课呈现，课堂是真正属于学生的，通过学生自主参与变题改题发挥学生主观能动性。

一题一课的优势在于课堂内容的紧密联系性。笔者在初始阶段设计本堂课时想着是否能够通过一个图将所有知识点联系。因此由一个圆这个大环境下引出，在圆中加入一些线段。但在教学设计上串联最后失败，线条的取消与加入将原图变得生硬。一题一课需要一定的功底，因此这也给此堂课留下了一个缺陷，也给自己留下了一个遗憾。但课堂教学之路不停，笔者将继续尝试。

（三）课堂自主性

本堂课在教学过程中，都是以教师引导为主。但好的课堂教师应是学生课堂的合作者。因此，在课后，我试想着课堂可否完全归还于学生。给出圆，让学生在圆中添加线段，并让学生出题，大家一起解决，总结方法。这是一堂复习课，学生已经有了一定的知识储备，放手让学生去做，既能调动学生学习数学的积极性，也能使学生体会到自身的主人翁意识。

本节课是借班上课，往往会存在学生与教师的磨合期，因此让学生去总结知识点，并添加线段，请全班一起动起来应是一个不错的方式。但此类课堂应是虽是放手，教师在引导过程中应要给学生一条主线，在预设环节需要更充分的思考。思考学生可能出现的变试题，以及在放手操作和整堂课主题之间的联系与衔接。在课堂上曾经看到过一张PPT，本节课只有一道题，通过学生的合作参与将一节课的知识点和内容进行呈现。

（四）运用多媒体技术

数据分析能帮助教师更好地掌握学生学习情况。在以往的课堂教学过程中，教师若想准确了解学生的实际掌握情况，唯一的方式可能在于课后作业以及课后检测，对整堂课的把握没有明确的概念。而利用平板的辅助，教师可以明确自身上课的有效性以及了解学生对于哪一块内容是存在问题的。能够及时针对学生的学情及时调整课堂节奏，使课堂真正做到有效。

学生对于平板这一类新型事物的热情性是比较高的，我们都知道兴趣是最好的老师，学生有了一定兴趣，那么对于数学的学习就会更感兴趣，学生听讲的专注度也会相对来说提高。平板由于它自身带有的可以观看视频，拍照上传，网上查询资料的优点，学生也乐意用这种方式。并且在学习过程中我们会对学生进行分组，小组之间会形成良性竞争。并且学生个人在学习过程中，每答对一题，系统会给予一定的金币激励，教师针对学生上课表现也可以学生一些小红花之类的奖励，让每个学生都能获得满足感和充实感。学生通过答题会有一个积分排行榜，这也能促进学生之间的良性竞争[2]。

针对学生的个体差异性，因材施教不失为一种好方法。我们也都知道教学过程中若能有效实行因材施教，对学生的数学学习有较大的作用。借助于平板，我们可以针对学生的实际学情，分层布置作业，让每一个学生在数学学习过程中都能吃饱、吃好，也让每个学生都能感受到跳一跳就能够得到。并且，学生的每一次作业也都可以形成一本电子错题本，这本错题本根据知识点的不同进行分类，能快速、有效地形成，节省学生很多时间；学生和教师都能够快速准确地掌握学情。若从初一坚持到初三，对学生来说也是一份宝藏。

（五）课堂有效性

评价一节复习课好与不好，我想课堂有效性势必是一个重要的评价指标，如：学生能否从这堂课得到提升，学生能否通过课堂将未解决的问题得到解决等。

学习最近发展区理论表明，复习课的开展应基于学生已有的知识和能力，在实施过程中不流于表面，真正做到复习有效可行是值得初中数学老师思考的一个重要问题。我们在初中章节复习课的复习过程中应当多思考，多实践，多交流和学习优秀的复习策略和方法。